数控机床定位胶结合面建模及参数识别方法*

刘雅荣

（长春职业技术学院工程技术分院，长春 130033）

数控机床定位胶结合面建模及参数识别方法*

刘雅荣

（长春职业技术学院工程技术分院，长春 130033）

文章提出采用正交异性模型的方法设置定位胶结合面的材料参数。首先分析了目前虚拟材料方法的不足，然后推导了正交异性模型结合部3个方向平移刚度和2个方向弯曲刚度的求解方法，之后以质量块和定位胶组成系统的模态性能为对象，研究了材料参数Ey、Gxy、Gzy的求解方法，最后对系统的模态性能进行了仿真分析。结果表明系统固有频率仿真误差绝对值小于1.69%，振型与实际吻合很好，从而验证了文中方法的正确性。

数控机床；结合面建模；参数识别；正交异性模型

0 引言

数控机床的不同零件通过结合面的方式联接，固定结合面是常见的一种联接方式，比如立柱通过螺栓固定安装在床身上。由于立柱和床身的两个接触表面都存在粗糙度，导致两个零件的实际接触面积远远小于理论接触面积［1］。为了增大两者的接触面积，从而提高联接稳定性，工程上一般通过研磨［2］的方法减小接触表面的粗糙度，但该方法比较费时。另一种方法是在立柱和床身之间灌注定位胶，待定位胶凝固后，通过螺栓将立柱拧紧在床身上。由于定位胶流动性较好，使得立柱与床身之间的接触面积增大，从而提高了两者的联接刚度［3］。

目前对数控机床整机的静动态性能进行有限元仿真时，立柱与床身之间的结合面通常通过弹簧单元［4-6］建模，即在螺栓联接位置添加弹簧单元，并赋予刚度和阻尼值。当立柱与床身之间存在定位胶时，由于定位胶的存在面积太大，且受力情况复杂，难以通过弹簧建模，通常采用“虚拟材料［7-8］”的方法建模，即在立柱与床身之间设置一块薄的实体块，并调整实体块的材料属性使得建立的模型与实际相符。本文在对目前方法研究的基础上，提出新的正交异性模型对结合面建模，利用模型各方向刚度特性的独立性，较好地反映定位胶结合部的特性。

1 目前虚拟材料参数设置的不足

文献［7-8］对虚拟材料的参数设置方法进行了研究，但设置参数后实体块的材料属性为各向同性。由于各向同性材料的三个常用参数弹性模量E、剪切模量G和泊松比μ存在式（1）的关系：

可以看出，材料属性可以通过G、μ和E中的两个确定。比如，当设置材料的弹性模量和泊松比后，材料的剪切模量也确定了，而且实体块沿x、y、z向的剪切模量被认为相等。但实际情况下，由于结合面的形状、螺栓布置方式不同，会导致实体块沿x、y、z向的材料属性不同。以某双立柱机床为例，假设立柱与床身的结合面如图1所示，立柱通过左右两侧各6个螺栓固定在床身上，在结合面之间灌胶。当图1中的实体块发生沿x向和z向的剪切变形时，如果设置各项同性，沿x向和z向的剪切刚度相同；但实际情况下，沿x向和z向的剪切刚度可能相差很大。

图1 定位胶结合部的接触面

机械结构中普遍存在一些板材，由于内部筋板布局不同，导致沿不同方向表现出的力学性能不同。工程上常采用“正交异性板［9-10］”对其建模，即：采用外观轮廓与研究对象相同、并可以使用正交异性材料赋予材料属性的实心板。本文借助“正交异性板”的概念，建立定位胶结合面的正交异性模型，通过设置模型的材料参数，赋予定位胶结合部不同方向的力学性能。

2 正交异性模型的建立

对于定位胶结合面，正交异性模型表现为结合部3个方向的平移刚度和2个方向的弯曲刚度。假设某正交异性模型的接触面积为A，厚度为h，平移刚度和弯曲刚度分别如图2和图3所示。

图2 正交异性模型的平移刚度

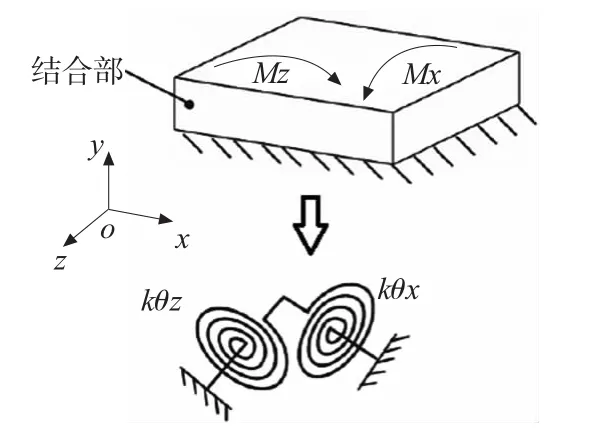
图3 正交异性模型的弯曲刚度

（1）沿y轴拉压变形的刚度

当模型受到沿y轴的力Fy时，结合部发生沿y轴的变形，变形量为d y，如图4所示。假设模型y方向的刚度为ky，则：

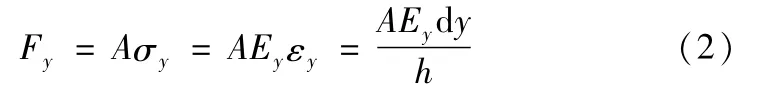
式中，σy、Ey、εy分别为模型y向的应力、弹性模量和应变。从而得到刚度ky为：

图4 结合部沿y向的变形

（2）沿x轴和z轴剪切变形的刚度

当模型受到沿x向或z向的载荷Fx或Fz时，模型发生剪切变形，变形量分别为d x或d z。以x向剪切刚度为例（图5），假设模型x向的刚度为kx，则结合部的受力变形关系为：

式中，τxy、Gxy、γxy分别为沿x向加载时在垂直于y向平面内的剪切应力、剪切模量和剪切应变。则刚度kx为：

图5 结合部沿x向受力变形

同理，沿z向的剪切刚度kz为：

式中，Gzy为沿z向加载时在垂直于y向平面内的剪切模量。

（3）绕x轴和z轴的弯曲刚度

以绕x轴的弯曲刚度（图6）为例，模型受到绕x轴的弯矩Mx时发生弯曲变形，可以用图6中的角度θx表示变形量。设模型绕x轴的弯曲刚度为kθx，则：

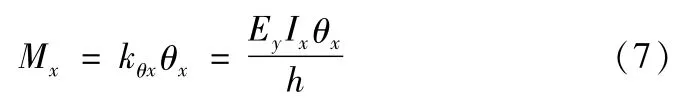
式中，Ix为接触面A以x轴的平行线为中性轴的抗弯截面系数。因此，刚度kθx为：

图6 结合部绕x轴的受力变形

同理，绕z轴的弯曲刚度kθz为：

式中，Iz为接触面A以z轴的平行线为中性轴的抗弯截面系数。

根据式（3）、（5）、（6）、（8）、（9）可以看出，材料参数Ey、Gxy、Gzy影响3个平移刚度和2个弯曲刚度，而其它材料参数没有影响。因此，本文通过设置Ey、Gxy、Gzy的参数，从而建立定位胶结合面的模型。

3 正交异性模型模态参数的辨识

本文以图7所示的模型为例，介绍正交异性模型模态参数的辨识方法。两个刚性质量块由正交异性模型的结合部联接，质量块1的底面固定，质量块2受到载荷。假设质量块2的质量为m，绕z轴的惯性矩为Jz，绕x轴的惯性矩为Jx，结合部的接触面积为A，厚度为h。

图7 正交异性模型模态验证对象

（1）沿y轴平移振动

由刚度ky可以得到沿y轴平移振动的频率fy为：

因此，Ey的表达式为：

（2）沿x轴和z轴平移变形

由刚度kx可以得到沿x轴平移振动的频率fx为：

因此，Gxy的表达式为：

同理，Gzy的表达式为：

（3）绕x轴和z轴旋转变形

由刚度kθx可以得到绕x轴旋转振动频率为：

式中Ey可以由kθx计算得到：

同理，Ey也可以由kθz计算得到：

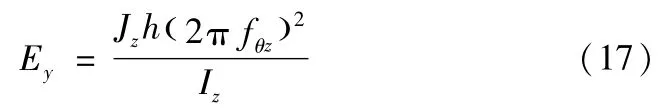
由以上分析可以看出，Gxy可以由式（13）求解，Gzy可以由式（14）求解，而Ey可以通过式（11）、（16）和（17）求解。实际情况下，沿x轴的平移振动往往与绕z轴的旋转振动同时存在，沿z轴的平移振动往往与绕x轴的旋转振动同时存在，如图8所示。

图8 正交异性模型组合变形

对图8a的组合变形进行分析：沿x轴平移振动与绕z轴旋转振动组合变形时，质量块2发生旋转，惯量为Jz；剪切刚度kx的力臂为0.5l，与弯曲刚度kθz串联形成系统的总刚度kxθz。此时振动频率为：

因此kxθz的表达式为：

对图8b的组合变形进行分析：沿z轴平移振动与绕x轴旋转振动组合变形时，质量块2发生旋转，惯量为Jx；剪切刚度kz的力臂为0.5l，与弯曲刚度kθx串联形成系统的总刚度kzθx。此时振动频率为：

因此kzθx的表达式为：

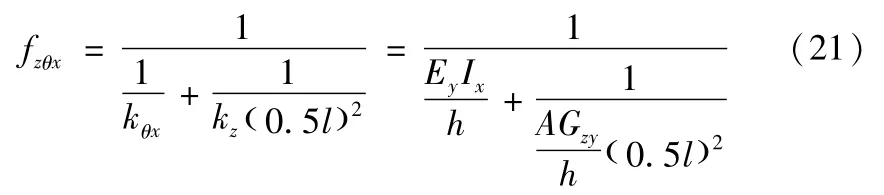
由于通常无法得到完全的剪切变形，可以由式（11）计算 Ey，然后由式（18）和（19）计算 Gxy，由式（20）和（21）计算Gzy。

4 正交异性模型验证

以图7所示的系统块为对象，假设质量块的密度Ρ=1000 kg/m3，l=1 m，计算得到质量块2的质量m=1000 kg，转动惯量分别为Jx=Jz=416.7 kg·m2，结合面的接触面积A=1 m2，厚度h=0.01m。已知系统的振动频率和对应的结合部变形情况［11］，如表1所示。

表1 验证对象的变形和频率

由表1和式（11），可以求解Ey；然后由式（18）和（19）计算Gxy；最后由式（20）和（21）计算Gzy。计算结果如表2所示。

表2 验证对象的弹性参数

将表2的弹性参数代入图7b的有限元模型，求解得到对应的振型和振动频率，并与表1中的数据进行对比，如表3所示。由表3可以看出，本文提出的正交异性模型考虑了不同方向的弹性参数，从而很好地反映了定位胶结合面的模态特性。

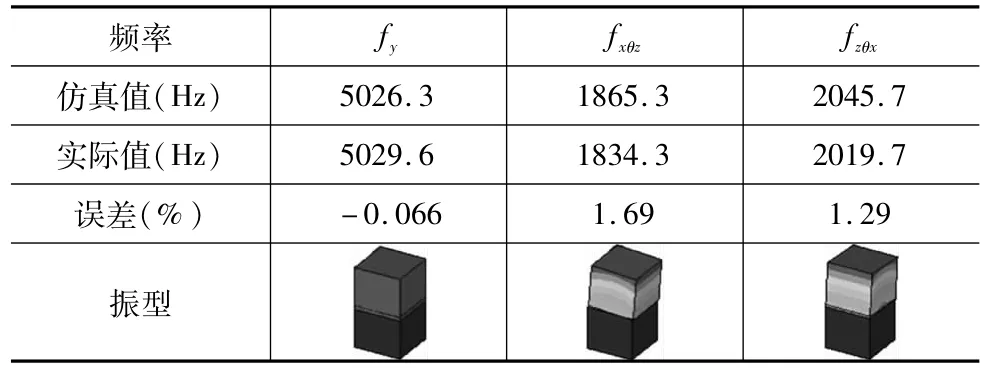
表3 验证对象的仿真与实际结果对比

5 结论

本文以数控机床定位胶结合面为研究对象，针对目前虚拟材料设置时材料属性各向同性、不能反映材料实际变形的缺点，提出建立定位胶结合面的正交异性模型。通过设置模型的材料参数Ey、Gxy和Gzy，从而可以赋予定位胶结合部不同方向的力学性能。以两个定位块和定位胶结合部组成系统的模态性能为对象，推导了弹性参数与系统3个振动频率的关系，仿真结果表明固有频率仿真误差绝对值小于1.69%，振型与实际吻合很好，从而验证了本文方法的正确性。

［1］周喜峰，汪惠芬，刘婷婷.GA-BP在数控机床结合面动态特性建模中的应用［J］.组合机床与自动化加工技术，2012（2）：12-15.

［2］袁军堂，夏玲玲，汪振华，等.灌胶结合面对数控机床动态性能影响研究［J］.南京理工大学学报，2012，36（6）：1010-1014.

［3］王志勇，胡小秋，郭丹峰.机床灌胶结合面特性参数试验及预测［J］.制造技术与机床，2011（12）：145-148.

［4］Kolluru K，Axinte D.Novel ancillary device forminimising machining vibrations in thin wall assemblies［J］.International Journal of Machine Tools&Manufacture，2014，85（10）：79-86.

［5］Agapiou JS.Estimating the static stiffness for a spindle-toolholder-tooling system［J］.Machining Science and Technology，2008，12（1）：77-99.

［6］Jeong J，Kang E，Jeong J.Equivalent stiffness modeling of linear motion guide ways for stage systems［J］.International Journal of Precision Engineering and Manufacturing，2014，15（9）：1987-1993.

［7］田红亮，刘芙蓉，方子帆，等.引入各向同性虚拟材料的固定结合部模型［J］.振动工程学报，2013，26（4）：561-573.

［8］黄开放，金建新.基于虚拟材料方法的螺栓预紧力模拟的研究［J］.机械设计与制造，2012（8）：148-150.

［9］李成，郑艳萍，吴跷铃，等.结构连接区开口正交各向异性板的应力仿真分析［J］.机械设计与研究，2007，23（2）：6-7，17.

［10］姚辽军，赵美英，周银华.不同孔径复合材料层合板应变集中及失效强度分析［J］.机械科学与技术，2011，30（5）：761-764.

［11］周志飞.立式加工中心灌胶结合面静动态性能分析［D］.长春：吉林大学，2009.

（编辑 赵蓉）（编辑 赵蓉）

Modeling and Parameter Identification for Positioning Adhesive Joint Surface of Machine Tools

LIU Ya-rong
（School of Engineering Technology，Changchun Vocational Institute of Technology，Changchun 130033，China）

Material parameters of positioning adhesive joint surface were set using orthotropic model.Weakness of the commonly used virtual material method was analysed firstly.Then，three translational stiffnesses and two bending stiffness of the orthotropic model were deduced.Taking a system composed by two mass blocks and a positioning adhesive joint surface as an example，relationship between modal characteristics and material parameters were deduced.At last，modal characteristics of the system were simulated.The simulation results show that absolute values of the natural frequencies were less than 1.69%，and the modal shapes were in good agreement with the actual shapes.

numerical control machine tool；joint surface modeling；parameter identification；orthotropic model

TH145.9；TG65

A

1001-2265（2015）04-0067-04 DOI：10.13462/j.cnki.mmtamt.2015.04.017

2014-12-06；

2015-01-04

国家自然科学基金资助项目（51075045）

刘雅荣（1969—），女，满族，长春人，长春职业技术学院副教授，研究方向为机电一体化技术，（E-mail）liuyarongset@126.com。