“S”形精度检验试件的简化重构与优化研究*
2015-11-03郑从志边志远赵旭综
杜 丽,郑从志,边志远,赵旭综,王 伟
(电子科技大学机械电子工程学院,成都 611731)
“S”形精度检验试件的简化重构与优化研究*
杜 丽,郑从志,边志远,赵旭综,王 伟
(电子科技大学机械电子工程学院,成都 611731)
“S”形精度检验试件作为一种新的五轴数控机床精度检验试件,目前已得到一定的推广,但根据ISO标准提出的试件通用、简化及工程化要求,仍需进一步完善S试件的构型。研究了基于三次均匀B样条插值简化“S”形检验试件的方法,通过重新调整控制点重构“S”形检验试件,并对简化前后的“S”形检验试件的典型特征,如开闭角、扭曲角、曲率及连续性等进行了对比分析,通过UG软件进行了加工编程,计算和对比了加工新旧“S”形检验试件的理想速度、加速度,证明了新“S”形检验试件的可行性,为“S”形检验试件的标准化推广提供了依据,有助于全面了解“S”形检验试件的几何和加工特性。
“S”形检验试件;插值逼近;重构与优化;开闭角;扭曲角
0 引言
随着制造业的发展,人们对数控机床的要求越来越高,数控机床也正朝着高速高精度的方向发展[1],因此对数控机床加工性能检验也越来越重要。目前国际上比较有名的机床检验试件,如美国的NAS979检验试件[2]、日本的四角锥台检验试件[3-4]和德国的梅赛德斯检验试件等,仅能检验机床静止或低速状态下的各项精度,对于机床在高速工作状态下的检测无能为力。由中航工业成都飞机工业公司提出的“S”形检验试件[5]能在一定程度上实现对五轴数控机床的动态加工性能检测,在机床行业引起了强烈反响。
“S”形检验试件(以下简称S试件)作为一种新的机床检验试件,目前相关公开的研究还比较少。文献[6]分析了不同参数对于S试件动态跟随误差的影响,揭示了进给伺服参数对S试件轮廓误差的影响规律;文献[7]运用有限元软件ANSYS对S试件静态变形、法向刚度及模态参数进行了计算,并通过敲击实验验证模态分析结果的准确性。文献[8]研究了基于S试件的机床误差的溯源方法;文献[9]对S试件型面误差的可视化技术进行了研究。
上述研究从不同方面对S试件进行了研究,但从ISO标准化的试件通用、简单和工程化等方面考虑,仍需开展对S试件模型的简化重构和优化等方面研究,以加快S试件国际化标准的步伐,因此开展对S试件的造型与简化重构分析研究具有重要的实际意义。本文重点对S试件上下样条曲线造型原理、上下样条曲线插值以及通过调整控制点重构上下样条曲线进行了研究,为S试件的简化重构提供理论参考。
1 S试件上下基线生成原理分析
1.1 三次均匀B样条插值算法
B样条的概念最初由Schoenberg于40年代中提出来的[10],如今已得到很大的发展。中国发明专利CN200710048269.7指出S试件直纹面的上下两条基线通过给定的各50个型值点采用3次均匀B样条曲线构建[2]。
B样条的数学表述式如下所示:

式(1)中Pi(i=0,1,···,n),是B样条曲线的控制点,将各控制点连接起来就可以得到曲线的控制多边形。Ni,m(u)是样条曲线基函数,m表示样条曲线的次数,基函数是B样条曲线的核心部分,其递推公式就是通过基函数实现的。u是节点序列。
采用德布尔递推算法可建立B样条曲线,B样条基函数的德布尔递推公式如下所示:

式(2)中:
(u0,…,um-1,um,…,un,un+1,…,un+m-1,un+m)是B样条基函数的节点向量。
由公式(2)可知高次B样条基函数是两个比其低一阶的B样条基函数的线性组合,也就是说Ni,m(u)可以通过Ni,m-1(u)和Ni+1,m-1(u)递推得到。而且在推导过程中涉及到 m+2个节点,即:ui,ui+1,…,ui+m+1,这些节点向量组成了B样条基函数的支撑区间[ui,ui+m+1],通过公式(2)就可以推导出三次B样条曲线的基函数表达式:
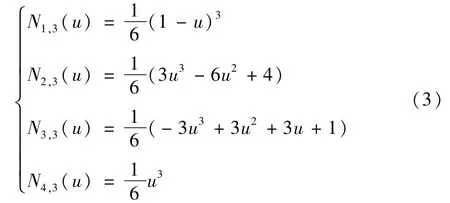
1.2 插值边界条件分析
通过三次均匀B样条插值,人们虽然可以得到一条均匀三次B样条曲线,但一般情况下生成的三次B样条曲线段的两端既不在控制多边形的边上,更不通过首、末顶点。实际上人们总希望所设计的曲线在给定点起始或终止,且具有确定的切线方向,还要求满足边界插值条件,工程上一般采用四重节点进行边界控制[11],S试件上下样条曲线的边界控制亦是如此。由式(1)和式(3)可推导出四重节点时三次B样条曲线各段的基函数表达式,这里不再详述。
1.3 型值点求解控制点算法
在实际工程中,人们往往只已知型值点,而控制点未知,S试件亦是如此,它只定义了上下样条曲线各通过的50个型值点,这便需要我们分析型值点和控制点间的关系。为方便起见,记Qi(0)为Qi(第i个型值点),当采用四重节点且三次B样条曲线段数不少于5段时,有式(5)成立

在方程组(4)中,方程数为n(型值点数量为n),欲求的控制点数为n+2,故要对方程组求解还需再加上两个条件。与三次样条函数插值类似,我们补充两个端点条件。设首末端切向量为已知,令:
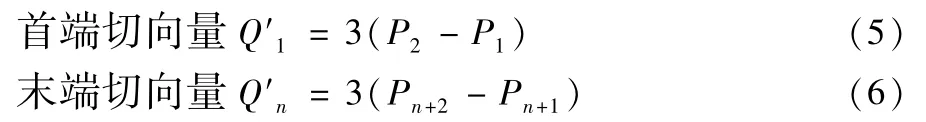
联立式(4)、(5)和(6)即可由已知的n个型值点求出给定切向量和自由端条件下的n+2个控制点,其中S件上下样条曲线插值采用自由端条件。将上述推导条件和公式在Matlab中编写相应的算法,即可绘制出S件的上下两条样条曲线,如图1所示,其中图中红圈为上下50个型值点。在三维造型软件中通过上下两条样条曲线扫掠生成直纹面,再将直纹面法向加厚8mm,加上基座,便可构造出S形检验试件三维模型,如图2所示。

图1 S试件上、下基线

图2 S试件三维模型
2 S件上下基线简化重构
2.1 控制点初步调整
由文献[7]知,由于构造S试件的型值点数据存在X方向不单调,故通过简单的插值方法构造的S曲线都易产生震荡,因此本文将通过从控制点入手,通过调节控制点,用尽可能少的控制点去逼近原来的三次B样条基线。在UG中经过反复调整控制点,最终将控制点数量减少到最少,即8个,图3是下基线初步调整结果。
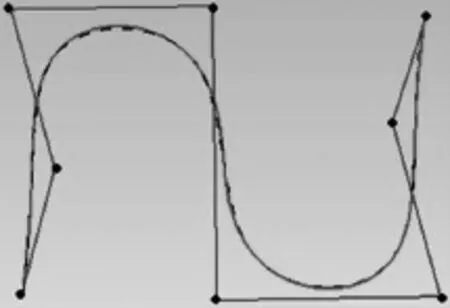
图3 8个控制点下S基线
图3中依次为8个控制点及其控制多边形和两条S曲线,整体上看原S曲线与新生成曲线基本重合,实线为原S试件下基线,虚线为新生成的S试件下基线。图4为其局部放大图。由图4知,放大后,两条S曲线间并不重合,而是存在细微的间隙。
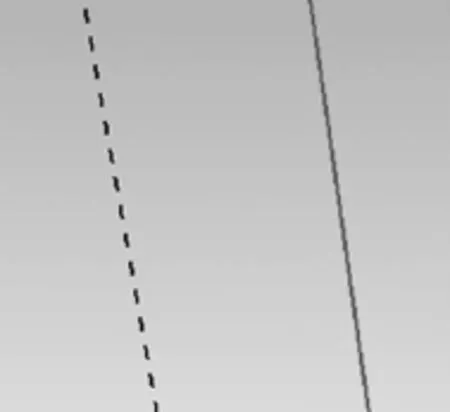
图4 S件下基线逼近局部放大
2.2 控制点调整优化算法
由2.1知,通过不断调整控制点,我们可以得到一条非常逼近与原S曲线的新S曲线,但无法对得到的结果进行评价,更无法证明结果的优越性,针对此问题,需建立一个正确的评价方法。本节以点到参数曲线的最小距离和为评价标准,即在新生成的S曲线上等弧长取500个采样点,计算每个采样点到对应原S曲线最小距离并求和。
当对控制点进行调整时,由于要保证新S曲线与原S曲线首末端保持重合,故只对中间的6个控制进行调整,调整时从左至右依次对相邻的控制点进行移动。先以一定的步长t沿X轴方向移动,反复比较得到最小距离和sum{min(di)}条件下该点最优X轴坐标,其中i=1,2,3,…,500;再以相同的步长沿Y轴方向移动,反复比较得到最小距离和sum{min(di)}条件下该点最优Y轴坐标,由此反复循环便可以得到一定步长t下,最小距离和sum{min(di)}最小时各个控制点的最优坐标。以单个控制点X方向坐标调整为例,其调整算法流程图如图5所示。
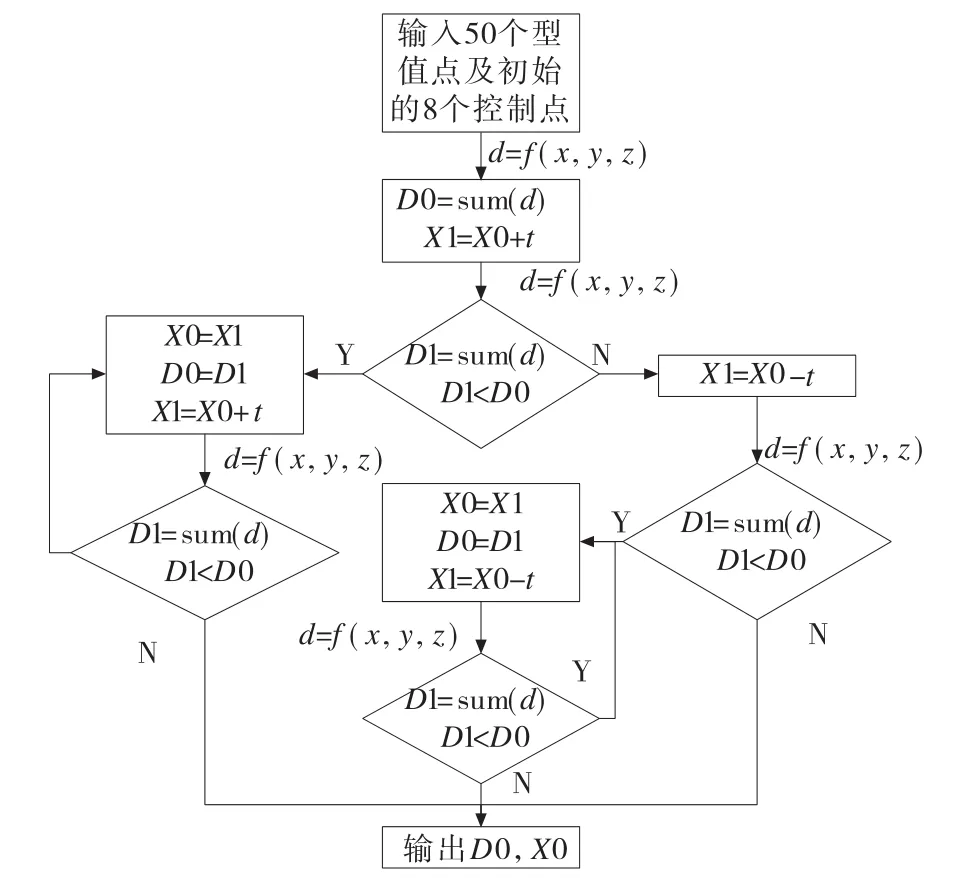
图5 X坐标调整流程图
表1是下基线调整前后8个控制点点坐标,第一组为初始时8个控制点坐标,其中:

第二组为步长t=0.5mm时调整后的8个控制点坐标,其中:

第三组为将第二组的8个点坐标按四舍五入法则全部圆整为整数,在步长t=1mm条件下调整后的8个控制点坐标,其中:

易知,初步调整后,总间隙减小了近25%,最大间隙也有所减小。圆整前后宏观上变化不大,细微之处需进一步比较分析。
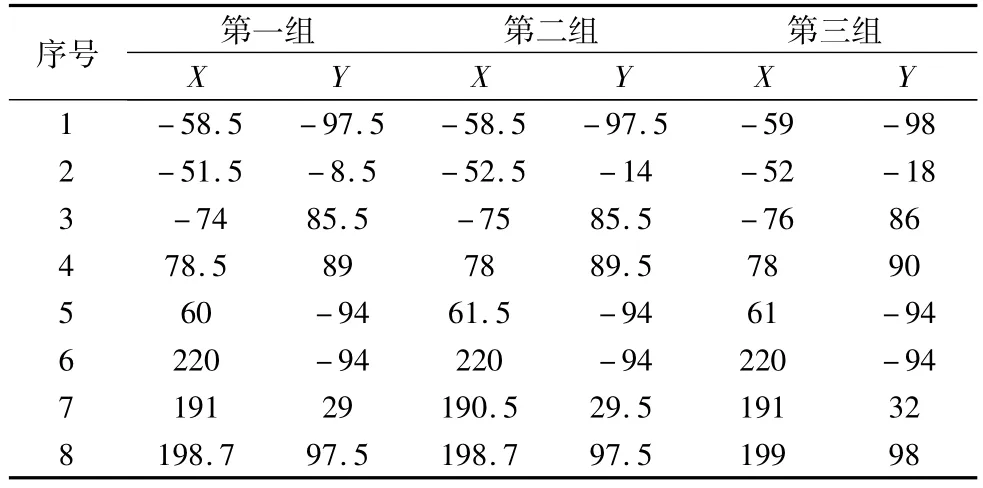
表1 三组控制点坐标
3 三种S件特性对比分析
从第2节的分析中我们知道,通过直接调整控制点逼近原S试件基线取得了较为满意的结果,然而仍无法证明通过逼近后生成的S曲线构造的新S试件能否满足原有的检测要求,因此需将新构造的S试件与原S试件的各项典型特性进行比较。为方便叙述,我们将原S试件编号为S0,步长t为0.5时,通过调整算法得到的第一组坐标生成的S试件为S1,将第一组坐标圆整后重新调整生成的S试件为S2。本节将从S试件的几何特性和加工特性两个方向对上述三种S试件进行对比分析。
3.1 几何特性对比分析
3.1.1 扭曲角对比分析
扭曲角是直纹面的典型特征之一,扭曲角的存在使刀具无法贴合加工表面,加工时易产生刀痕或过切,严重时直接导致零件报废,因此要求机床有较高的联动精度以反映实际的加工工况。图6是三种S试件的扭曲角分布图。由图6可知,S2的扭曲角分布从幅值和趋势分布上都较S1更加接近S0,其中最大扭曲角γ0=6.651°,γ1=8.391°,γ2=7.078°。另外S0的扭曲角变化近似左右对称,而S2的扭曲角分布左右不对称,变化更加多样,加工时刀轴矢量变化更加多样。

图6 三种S件扭曲角分布
3.1.2 开闭角对比分析
开闭角主要反映刀具的空间姿态,S试件典型几何特征之一。设待加工曲面的法向向量和底座平面的法向向量之间的夹角为α,当夹角大于90度,定义为开角,小于90度,定义为闭角。图7是三种S试件开闭角分布情况,由图7知,三种S试件的开闭角分布非常接近,并无太大区别,说明在开闭角特性上三种试件已无太大差别。

图7 开闭角分布
3.1.3 曲线曲面连续性对比分析
对于复杂曲面加工,曲率的非均匀变化将直接引起加工过程中铣削力的变化,引起刀具和零件的振动,破坏机床的稳定性。图8是依据曲率公式计算后得到的三种S试件下基线的曲率分布图。由图8知,在曲率分布上,圆整前后曲率并没有发生太大的变化,只是在峰值上有所微调,整体趋势与S0大致相同,局部峰值大于S0,达到了很好的逼近效果。

图8 下基线曲率分布
曲面连续性是S试件分析的一项重要特性。通过斑马线,可以检测S试件的G0-G2连续特性。图9分别是S0、S1和S2的斑马线检测结果。由图9可知,三种试件的G1、G2连续性分布基本一致,逼近效果非常好。

图9 三种S试件曲面连续性分析
3.2 加工特性对比分析
根据加工后置指令可以计算各轴的理想速度和加速度。假定进给速度Vf恒定,每段插补当量位移:

则每段插补时间△t=△s/Vf。对于五轴数控机床,其各个轴是联动的,因此其各轴增量(△x,△y,△z,△α,△γ)都应该在相应的△t内完成,故将各轴每段增量对时间△t微分便可得到各轴每段理想速度Vi,(i=1,2,…,5),再次对时间△t微分便可得到各轴每段理想加速度ai,(i=1,2,…,5)。取Vf=40mm/s,以转动轴C轴为例,图10是其理想速度,图11是其理想加速度。由图10和图11知,三种S试件的C轴的速度和加速度变化趋势基本保持一致,局部有微小变动,加速度在峰值上变化最大,新S试件在速度、加速度上很好地跟随了原S试件的速度、加速度变化。同时新S试件在速度和加速度上出现了更多的微小波动,对机床的加减速性能提出了更高的要求。

图10 C轴理想速度分布

图11 C轴理想加速度分布
4 结束语
S试件作为一种五轴机床精度检验试件,目前已在国内获得实际应用,并且正在加快其国际标准的步伐。本文针对ISO标准化的要求,对S试件进行了简化重构研究,通过对S试件构造原理的分析,进行了S试件上下基线的插值重构。通过从控制点入手,实现了以最少点位重构S试件,将得到的新S试件控制点进行了圆整优化,并且对新旧三种S试件各项特性参数的进行了分析对比,证明了新S试件的可行性,且圆整后的S试件更加接近原S试件,实现了对S试件的简化重构,对S试件的进一步研究和推广具有重要意义。
[1]鲁方霞,邓朝晖.数控机床的发展趋势及国内发展现状[J].工具技术,2006(3):44-48.
[2]NAS979:Uniform cutting test-NAS series.Metal Cutting E-quipment[R].NAS,USA,1969.
[3]TSUTSUMIM,YUMIZA D,UTSUMIK.Evaluation of synchronous motion in five-axis machining centers with a tilting rotary table[J].Journal of Advanced Mechanical Design,Systems and Manufacturing,2007,1:24-35.
[4]UTSUMI K,KOSUGI T,SAITO A,et al.Measurement method of geometric accuracy of five-axis controlled machining centers[J].Japan Society of Mechanical Engineering,2006,73(719):2293-2298.
[5]宋智勇,崔雅文.综合检测数控铣床精度的“S”形检测试件及其检测方法[P].中国:发明专利,CN101000285A,2007.1.16.
[6]霍彦波,丁杰雄,谢东,等.五轴数控机床转动轴与平动轴联动的轮廓误差仿真分析[J].组合机床与自动化加工技术,2012(3):21-25.
[7]赵波.“S”形检验试件数控侧铣振动分析及加工表面质量研究[D].C成都:电子科技大学,2013.
[8]杜丽,崔浪浪,赵波,等.基于S型检验试件的数控机床动态性能辨识新方法[J].制造技术与机床,2012(12):152-156.
[9]丁杰雄,谭阳,崔浪浪,等.一种五轴机床检验试件轮廓误差的处理与显示技术研究[J].组合机床与白动化加工技术,2012(10):39-43.
[10]Cox,M.Applications,The numerical evaluation of B-splines[J].Journal Inst Mathematics Applications,1972(10):134-149.
[11]朱心雄.自由曲线曲面造型技术[M].北京:科学出版社,2000.
(编辑 赵蓉)
Research on Reconstruction and optimization of The“S”Shaped Test Piece
DU Li,ZHENG Cong-zhi,BIAN Zhi-yuan,ZHAO Xu-dong,WANGWei
(School of Mechatronics Engineering,University of Electronic Science and Technology of China,Chengdu 611731,China)
As a new five-axis CNC machine precision test specimen,"S"shaped test piece has been promoted,but according to the requirement of ISO standards,deficiencies still existed.The paper studied the reconstruction of S shaped test piece by cubic B-spline interpolation,focused on re-adjusting the control points to approach and reconstruct the S shaped test piece,and made a comparative analysis on the typical characteristics of S shaped test piece,such as open-close angle,twist angle,curvature and so on,By UG software,the processing program was made,and the post command was got.Through the post command,the desired speed and acceleration of processing S shaped test piece were calculated and compared,the feasibility of the new S shaped test piece was proved,which helped us know the S shaped test piece comprehensively.
S shaped test piece;interpolation and approximation;reconstruction and optimization;open close angle;twist angle
TH161;TG506
A
1001-2265(2015)04-0005-05 DOI:10.13462/j.cnki.mmtamt.2015.04.002
2014-06-28;
2014-08-04
国家科技重大专项(2014ZX04014-031)
杜丽(1970—),女,四川成都人,电子科技大学教授,博士,研究方向为先进制造技术,精密机床精度检测;通讯作者:郑从志(1988—),男,湖南耒阳人,电子科技大学硕士研究生,研究方向为机床精度检测,(E-mail)fxz_7@foxmail.com。
