面向PCB圆形基准点的权重式椭圆拟合定位方法*

岑 誉，高 健，曾 友，简川霞

（广东工业大学机械装备制造与控制技术教育部重点实验室，广州 510006）

面向PCB圆形基准点的权重式椭圆拟合定位方法*

岑 誉，高 健，曾 友，简川霞

（广东工业大学机械装备制造与控制技术教育部重点实验室，广州 510006）

针对贴片机视觉系统对印刷电路板（PCB）圆形基准点快速精密定位的要求，提出基于形态学的基准点区域提取方法，对约化后的基准点进行像素级边缘提取，进而采用一维曲线拟合法提取出亚像素级边缘；在此基础上，提出一种圆形基准点边缘轮廓的权重式椭圆拟合定位算法，减少边缘轮廓点大离群值对拟合精度的影响，获到高精度的基准点中心位置。该算法通过设置椭圆约束条件，可避免零解和成比例解的出现，提高计算的速度和精度。仿真实验结果表明，所提的方法耗时25ms左右，基准点中心的位置误差小于0.03pixel，相比于其它定位方法，该方法在耗时和定位精度方面具有明显优势。在实验室搭建的视觉检测平台上开展进一步的实验验证，对实际采集到的PCB基准点图像可实现快速精确的基准点中心坐标提取，基准点拟合椭圆的形状误差均值为0.1pixel，能满足贴片机视觉系统快速精密的定位要求。

PCB；圆形基准点；亚像素；边缘提取；加权椭圆拟合

0 引言

在电子组装领域中，贴片机是典型的高速高精度专用电子设备，它对生产效率和产品质量具有至关重要的作用。印刷电路板（Printed Circuit Board，简称PCB）基准点能确定PCB的偏转情况和元件的贴装位置。贴片机视觉系统对PCB基准点的定位精度直接影响到电子元件的贴装精度和速度。在各种基准点中，圆形基准点以其制作简单、易于识别和定位精度高等优点而得到广泛的应用。因此，对PCB圆形基准点进行鲁棒、快速、精确定位的研究，对加快我国电子贴装技术的发展具有重要的意义。

对圆形基准点定位的方法主要有灰度重心法、Hough变换法和圆拟合法。灰度重心法算法简单，速度较快，在基准点灰度分布均匀，形状对称的情况下能获得较好精度，但由于基准点不可避免造成的污染，加上光照的不均匀，该算法将出现较大误差。Hough变换将图像空间点变换为参数空间中，抗噪能力强，受残缺边缘的影响小，但该算法需对参数空间离散化，并逐点投票和记录，运算时间长，精度不够高。圆拟合法先提取基准点边缘轮廓，再对其进行标准圆拟合，获得圆心坐标，该方法实现简单，计算速度快，但其抗噪能力差，对圆的质量要求较高［1-2］。上述方法均是基于图像像素级的，这使基准点的定位精度受到很大的限制。

考虑到镜头镜片安装不可能绝对平行，摄像机也不可能与PCB绝对垂直，加上摄像机成像的原因，采集到的PCB基准图像中，原为圆形的基准点将成为椭圆形，若仍采用标准圆拟合法定位基准点中心，则必将导致定位精度的降低。因此，本文提出一种加权的椭圆拟合算法，实现圆形基准点的精确定位。先利用形态学的开运算获得基准点区域，再利用高斯滤波对图像进行平滑，接着通过先粗定位后精定位的方法提取基准点的亚像素边缘轮廓，最后利用加权的最小二乘法拟合椭圆，获得基准点中心坐标。

1 图像预处理

圆形基准点为铜质材料，反光作用强，但由于基准点材料的固有属性，加上工业环境的污染，摄像机成像等原因，采集到的基准点图像常常灰度不均匀，并包含很多杂质和缺陷，这将对基准点的精确定位造成很大影响，如图1所示。因此，在进行定位前对图像进行预处理十分重要。

图1 圆形基准点

图2 基准点区域提取

1.1 基于形态学的PCB基准点区域提取

所谓形态学处理是指用具有一定形态的结构元素去度量和提取图像的形状以达到图像分析和识别的目的［3］。

由于PCB基准点十分靠近电路和元件贴装位置，采集到的基准点图像包含很多无用背景，这对基准点的快速定位造成很大的影响。为此，必须提取感兴趣区域，减少后续图像处理和特征提取的时间。传统的感兴趣区域提取都是通过手动设置或者图像分割进行的，但手动设置灵活性差，而图像分割后依然保留较多的背景。考虑到开运算有一个非常有用的特性：当使用圆形或矩形的结构元时，区域中比结构元小的部分将被消除，而比结构元大的物体又能尽可能保留其面积和形状，本文提出基于形态学的感兴趣区域提取方法，利用开运算抑制基准点图像背景的小物体，提取出基准点区域。首先，通过最大类方差法对图像进行阈值分割，获得二值图像，突出基准点位置；然后，采用比基准点空旷区外径略小的圆作为结构元，对二值图像进行开运算，消除不必要背景，获得基准点的二值化区域；最后，取开运算后的区域与原图像的交集，获得新的区域即为约化后的基准点区域图像，如图2所示。

1.2 PCB基准点图像的平滑处理

由于受到摄像机、光源、环境、传输等因素的影响，采集到的图像往往存在噪声。噪声会恶化图像质量，对圆形基准点边缘的提取造成严重影响，降低最终拟合和定位的精度。均值滤波处理速度快，但它的频率响应是各项异性的，不能完全消除噪声，同时会导致边缘过分模糊；中值滤波处理速度慢，且滤波窗口越大，速度越慢，不适合贴片机视觉系统图像处理的实时性要求；高斯滤波是各向同性的，既能满意地抑制噪声，又能减少对边缘的模糊，处理速度和效果都能很好满足贴片机视觉系统的要求。因此采用高斯滤波进行图像平滑处理，二维高斯滤波器为：

式中，σ为高斯函数分布系数，r，c分别为行列坐标，滤波平滑效果由σ大小控制。由公式可知，二维高斯滤波器是可分的，因此能被高效地计算出来。设滤波前后图像函数分别为f（r，c）和h（r，c），则滤波过程可以用卷积表示：

经过高斯滤波后，图像的噪声明显降低，同时高斯滤波器的可分特性为后面的边缘提取做了有效准备。

2 PCB基准点的像素级边缘提取

边缘是指图像中像素灰度有阶跃变化或屋顶状变化的那些像素的集合［4］。由于图像传感器的特性和光学的衍射效应等影响，边缘并不是理想的阶跃边缘，而变成斜坡边缘，表现为前景灰度平滑过渡到背景灰度。传统的边缘检测都是基于像素级别的，且对噪声敏感，由于边缘平滑过渡和光照变化的影响，阈值选择不同或者当照明改变时所提取的边缘信息也不同，这将对基准点边缘的精确定位造成严重影响。为此，提出使用最佳的亚像素边缘检测对基准点的边缘进行提取。在此之前，需要先对基准点边缘做粗定位，鲁棒、精确地获得其像素级边缘幅度和方向。

2.1 最佳边缘检测准则

为了对边缘检测算法做出合理、有效的评价，Canny提出了最佳边缘检测的三个准则［5］：

（1）信噪比准则。具有最大的输出信噪比，即对边缘点的错检率和漏检率都要低。

（2）定位精度准则。具有好的定位性能，检测出来的边缘应尽可能靠近真实边缘的中心，即边缘位置的方差要最小化。

（3）单边缘响应准则。对于每个真正的边缘只返回唯一的边缘，避免多重响应，即单边缘产生多边缘的概率要低，伪边缘响应得到最大的抑制。

2.2 非最大抑制和滞后阈值分割

符合上述准则的理想边缘滤波器能用高斯滤波器的一阶导数来近似，该滤波算子称为Canny算子。由于对高斯滤波器求导后再和图像函数进行卷积与先对图像进行高斯滤波再进行求导的结果一样，即可以先平滑滤波消除噪声，再锐化得到边缘细节。因此，就可以充分利用图像预处理中高斯滤波得到的结果，即有：

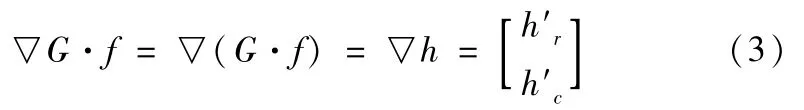
其中，边缘强度可用滤波后在待测像素点梯度大小来表示：

边缘的方向可以表示为：

判断待测点ei是否为边缘，可在梯度方向上判断该点的边缘幅度是否为其领域的最大值，即是否满足（ei＞ei-1）∧（ei＞ei+1）∧（ei≥t），其中t为边缘选择的阈值，这过程称为非最大抑制。然而，若选择高阈值，边缘会被分割成若干段；若选择低阈值，又会出现很多不相关的伪边缘。对此，应该采用一种特殊的边缘分割方法：滞后阈值分割［5］。滞后阈值采用双阈值，即低阈值T1和高阈值T2。边缘幅度比T2高的立即作为合格的边缘，比T1低的立即作为不合格的边缘。介于低阈值和高阈值的边缘点若能按某一路径与合格的边缘点相连时，才能作为边缘点被接受。通过滞后阈值分割，边缘点被连接起来。通过滞后阈值分割后，图像仍然包含很多非基准点边缘，考虑基准点的特征，利用周长和圆度特征对分割后的图像进行特征提取，最终获得基准点的像素级边缘，如图3所示。

3 PCB基准点的亚像素级边缘提取

在检测到像素级边缘，实现了粗定位后，要更精确地进行椭圆拟合，就必须对边缘轮廓进行亚像素精度提取。文献［6］对多种亚像素边缘检测算法作出了比较。考虑到经过像素级粗定位后，边缘点已经比较鲁棒、准确地提取出来，这样可将亚像素边缘检测的二维曲面拟合法转化为一维曲线拟合法。由于基于三次多项式的最小二乘曲线拟合法比较简单，易于实现，且对小块数字图像，已足够精确［4］。因此，采用三次多项式对边缘点及其梯度方向上邻域点的梯度值进行拟合，获得边缘点法线方向上的连续梯度函数，该函数的极大值点即为边缘点的亚像素坐标。

假设在边缘点梯度方向上建立坐标系GCS，像素级边缘点坐标为（xi，yi）（i=1，2，…，N），三次多项式形式为：

则最小二乘目标函数为：

要令目标函数I的值最小，根据多元函数极值的必要条件有：

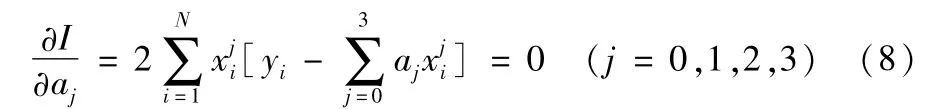
上式可写成关于参数a的正规方程组，令

则式（8）用矩阵形式表示如下：

可得出参数向量a的最小二乘解为：

由于亚像素边缘点的位置出现在函数二阶导数过零处，故令φ（x）＂=0即可求得其在GCS坐标系的坐标为该坐标加上像素级边缘点的坐标，即为亚像素点在图像坐标系的坐标。亚像素边缘提取结果如图4所示。

图3 像素级边缘

图4 亚像素级边缘

4 PCB基准点的权重式椭圆拟合

由于图像采集过程的影响，常将圆形基准点投影成椭圆形状，采用椭圆的方式拟合该基准点边缘轮廓，将得到更为准确的拟合结果，且由于圆是椭圆的特例，因此，椭圆拟合更有代表性。椭圆方程的隐式方程为：

式中，B=［a，b，c，d，e，f］T，CT=［x2，xy，y2，x，y，1］，且需满足b2-4ac＜0。通常，采用最小二乘法对边缘轮廓点进行椭圆拟合，其中包括代数距离误差法和几何距离误差法。代数距离误差法把边缘轮廓点坐标代入隐式方程得到这些点到理想椭圆的代数距离，通过对代数距离进行误差最小化来完成椭圆的拟合。几何距离误差法要先求出每个边缘轮廓点到理想椭圆的最短距离（正交距离），再使所有最短距离的平方和最小化来获得椭圆参数［7］。因为代数距离并没有明显的几何意义，而几何距离更贴近实际的椭圆拟合情况，所以几何距离误差法更准确、更稳定。但几何距离误差法涉及复杂的坐标变换和高阶方程的非线性求解，速度较慢，而代数距离误差法可通过线性方法求解，速度快，能满足实时性的要求。因此，采用代数距离误差法作为椭圆拟合的方法，几何距离误差法作为实验验证椭圆拟合效果和分析形状误差的方法。

传统的椭圆拟合常使用标准的最小二乘拟合法，并没考虑大的离群值的影响［8-9］。因此，与椭圆距离远的点占了很大的权重，这严重影响拟合精度。为减轻这些点的影响，引入权重函数ω（δi），先通过标准的最小二乘法计算出代数距离，再利用权重函数定义后续迭代中对应点的权重。为了使较远的离群值获得足够小的权值，选用Tukey权重函数，其定义为：

式中，τ为削波因子，δi为边缘点到椭圆的代数距离。为避免出现零解或成比例的解，以往常令a=1，结合椭圆约束条件b2-4ac＜0进行求解，导致求解过程限制多，不良数据计算占用时间较长，效率和精度较低。Fitzgibbon等［10-11］提出采用b2-4ac=-1的约束条件，既可以同时满足椭圆要求和避免零解或成比例解的出现，又能提高计算的速度和精度，写成矩阵形式即BTDB=1，其中

式中，S=（ΛG）T（ΛG）。Fitzgibbon等［10-11］证明了该矩阵方程只有唯一的正特征值，并且其对应的特征向量即为所求椭圆的拟合参数。椭圆拟合的结果如图5所示。根据所求参数，得到椭圆圆心坐标为

图5 权重式椭圆拟合结果

5 实验验证与分析

5.1 仿真实验

为了验证权重式椭圆拟合算法得有效性，利用计算机生成一张分辨率为640×512、圆心坐标为（320，256）的理想基准点图像，进行仿真实验。为验证算法的精度、速度和鲁棒性，特别添加了不同程度的干扰来模拟真实图像。本文的PCB基准点提取算法在Halcon软件中开发实现，其实验结果将与灰度重心法和传统的最小二乘圆拟合法作比较。实验描述如下：

实验1：利用Photoshop软件对图像进行羽化，令边缘模糊，如图6a。

实验2：为图像添加强度3%的椒盐噪声，降低图像质量，如图6b。

实验3：令基准点边缘出现凹凸缺陷，模拟边缘缺损和受污染情况，如图6c。

实验4：将基准点内部挖空，模拟真实图像光照不均和受污染情况，如图6d。

实验5：真实的基准点往往包含上述四种实验情况，将所有情况综合考虑，如图6e。

图6 不同实验条件下PCB基准点的位置提取

由图可见本文提出的方法能够鲁棒地定位基准点的圆心位置。每个实验分别重复10次，取其平均值得到表1的计算结果，以圆心的位置误差作为评价标准作图，如图7所示。

由表1和图7可知，本文算法的执行速度接近于算法简单的灰度重心法，但灰度重心法的定位精度在基准点边缘缺损、灰度不均等受污染情况下（如实验3、4、5）会受到严重影响，而本文算法几乎不受影响。传统的最小二乘圆拟合法将椭圆轮廓拟合成标准圆，且不考虑边缘轮廓离群值的影响（如实验3、5），既损失了定位精度，又增加了执行时间。由图7可见，本文算法在各种干扰情况下均能准确地定位到圆心位置，定位精度均优于其他两种方法。

图7 备种方法的位置误差

5.2 PCB基准点视觉定位系统实验

为验证本文方法的实用性，搭建了PCB基准点视觉定位系统，如图8所示。该实验平台摄像机的像素分辨率为122μm/pixel，基准点图像采集大小为640× 512。应用本文所提出的图像处理方法及基准点提取算法，得到的 PCB基准点定位坐标为（107.141，216.875），如图9所示。

图8 PCB基准点定位实验装置

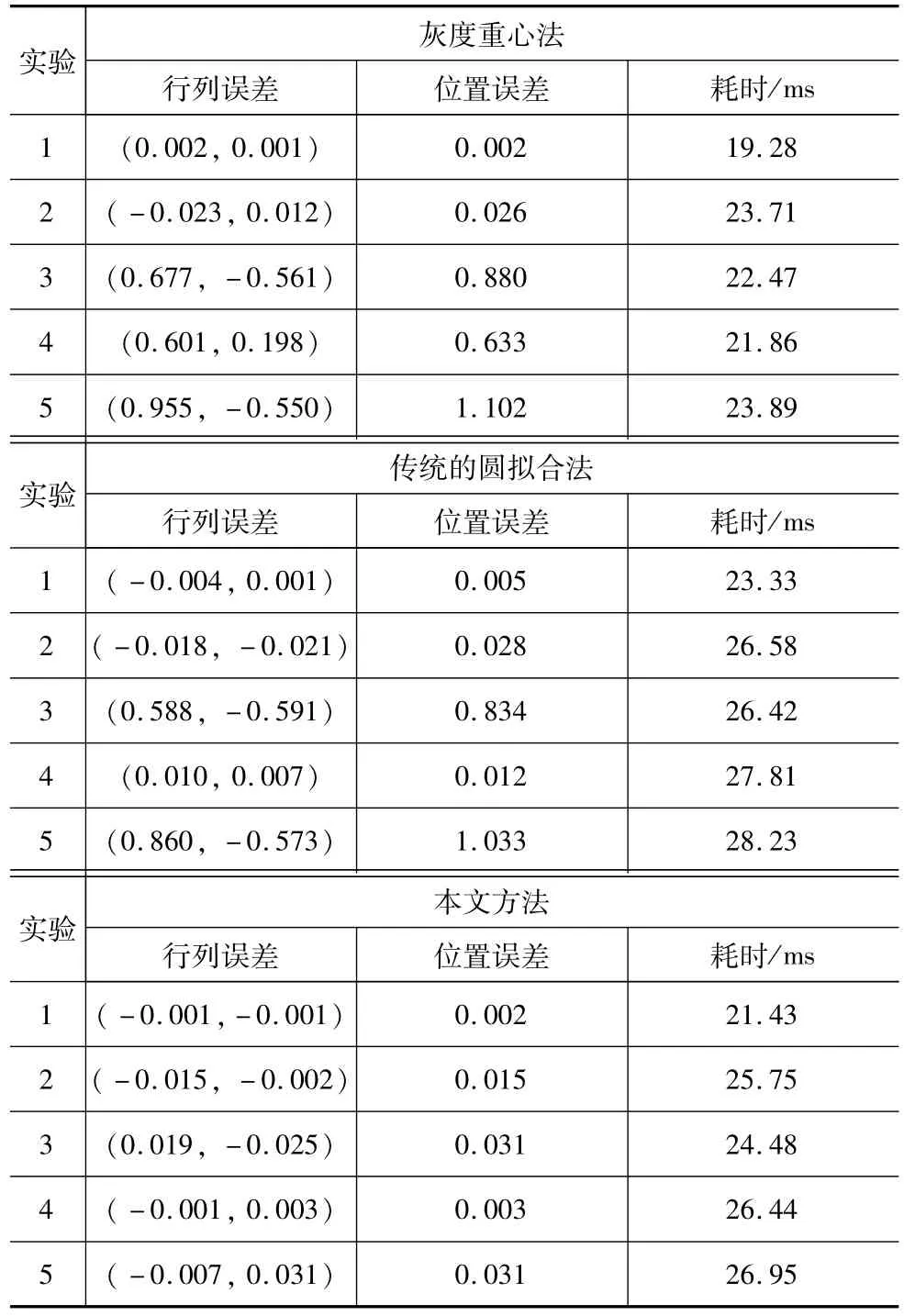
表1 基准点定位方法的结果比较（误差单位：pixel）

图9 PCB基准点定位结果

由于实验平台上进行的PCB视觉系统实验无绝对的标准位置可做参考，实验获得的基准点位置精度需用不同的方式来评价。因此，本文提出一种间接评价法，即使用基准点的边缘轮廓点到拟合椭圆的几何距离作为椭圆的形状误差来验证拟合效果。该方法定义边缘点在椭圆内部时，形状误差为负，在椭圆外部时，形状误差为正。经计算，本实验基准点图像拟合椭圆的形状误差绝对值最大值为0.247像素（实际距离30μm），最小值为0.001像素（实际距离0.122μm），均值为0.103像素（实际距离12.566μm）。图10显示了拟合椭圆形状误差的大小，其误差值均在±0.25像素以内，并以x轴作为回归轴。实验结果证明，本文提出的权重式椭圆拟合算法是可行的、有效的，能较好地满足PCB贴片机的高精度定位要求。

图10 拟合椭圆的形状误差

6 结论

为满足贴片机在PCB视觉检测和贴片过程中快速精密的定位要求，本文提出了面向PCB圆形基准点边缘轮廓的权重式椭圆拟合定位方法。首先，提出了基于形态学的基准点区域提取方法；接着根据最佳边缘检测准则，结合非最大抑制和滞后阈值分割对约化后的基准点图像进行像素级边缘提取，进而利用一维的曲线拟合法提取出亚像素精度的边缘轮廓；最后，提出对边缘轮廓进行加权的椭圆拟合，降低边缘离群值对拟合精度的影响，同时采用b2-4ac=-1的椭圆约束条件，提高拟合精度和减少拟合时间，最终获得PCB基准点的中心位置。

仿真实验结果表明，本文所提的定位方法耗时25ms左右，基准点中心的位置误差小于0.03像素，与其他方法对比，本文方法能够快速、精确地提取圆形基准点的中心坐标。在搭建的视觉定位［参考文献］

平台上进行真实图像实验，实验结果表明采用本文方法拟合的椭圆形状误差均值为0.1像素，满足贴片机视觉检测系统的定位要求。

［1］李瑛.圆形基准定位技术研究［D］.哈尔滨：哈尔滨工业大学，2012.

［2］王拯洲，许瑞华，胡炳樑.基于圆拟合的非完整圆激光光斑中心检测算法［J］.激光与红外，2013（6）：708-711.

［3］朱虹.数字图像技术与应用［M］.北京：机械工业出版社，2011.

［4］赵鹏.机器视觉理论及应用［M］.北京：电子工业出版社，2011.

［5］Canny J.A Computational Approach to Edge Detection［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence，1986，8（6）：679-698.

［6］张虎.亚像素技术与摄像机标定技术的研究［D］.南京：东南大学，2010.

［7］Sung JA，Rauh W.Least-squares orthogonal distances fitting of circle，sphere，ellipse，hyperbola，and parabola［J］. Pattern Recognition，2001，34：2283-2303.

［8］华瑞娟.多椭圆拟合的算法研究［D］.广州：暨南大学，2010.

［9］夏菁.椭圆拟合方法的比较研究［D］.广州：暨南大学，2007.

［10］Fitzgibbon A，Pilu M，Fisher R B.Direct least square fitting of ellipses［J］.IEEETransactions on Pattern Analysis& Machine Intelligence，1999，21（5）：476-480.

［11］Pilu M，Fitzgibbon A W，Fisher R B.Ellipse-specific direct least-square fitting［J］.International Conference on Image Processing，1996，3：599-602.

Weighted Ellipse Fitting Location Method for PCB Circular M ark

CEN Yu，GAO Jian，ZENG You，JIAN Chuan-xia
（Key Laboratory of Mechanical Equipment Manufacturing&Control Technology，Ministry of Education，Guangdong University of Technology，Guangzhou 510006，China）

In order to meet the chip mounter vision system requirement for the fast and precise location of circular mark on printed circuit board（PCB），a mark region extraction method based on the morphology was proposed.After that，the pixel edge was extracted from the simplified mark image and then the sub-pixel edge was extracted by one-dimensional curve fitting.On this basis，a location algorithm based on weighted ellipse fitting for circular mark edge contour was proposed to reduce the impact of large outliers of edge contour points and acquire high-precision mark centre position.The algorithm could avoid the zero and proportionable solutions and improve the computational speed and accuracy by setting elliptical constraint.The simulation experiment result indicates that with the proposed method，the elapsed time is about25ms，the position error of mark centre is less than 0.03pixel.The method has a significant advantage in elapsed time and precision over the other location methods.The further experiment testing on visual inspection platform indicates that them ark centre can be located fast and precisely from the real PCB mark image and the mean form errors of fitted ellipse are just0.1pixel，which meets the chip mounter visual system requirement for speediness and high precision.

PCB；circular mark；sub pixel；edge extraction；weighted ellipse fitting

TH161；TG506

A

1001-2265（2015）04-0019-05 DOI：10.13462/j.cnki.mmtamt.2015.04.005

2014-07-31

国家重点基础研究发展计划（973计划）项目（2011CB013104）；广东省高等学校科技创新重点项目（2012CXZD0020）；广东省战略性新兴产业专项资金（2012A080303004）

岑誉（1990—），广东封开人，男，广东工业大学硕士研究生，研究方向为机器视觉、图像处理和模式识别，（E-mail）lujincy@qq.com；高健（1964—），女，山东青岛人，广东工业大学教授，博导，博士，研究方向为在线检测和机器视觉技术。