基于拓扑优化与筋板布局的立柱轻量化设计*
2015-11-03刘成颖王立平
刘成颖,谭 锋,王立平
(1.清华大学a.机械工程系;b.精密超精密制造装备及控制北京市重点实验室,北京 100084;2.电子科技大学机械电子工程学院,成都 611731)
基于拓扑优化与筋板布局的立柱轻量化设计*
刘成颖1a,1b,谭 锋2,王立平1a,1b
(1.清华大学a.机械工程系;b.精密超精密制造装备及控制北京市重点实验室,北京 100084;2.电子科技大学机械电子工程学院,成都 611731)
为了实现机床立柱结构的轻量化设计,对立柱进行拓扑优化研究,根据拓扑优化的材料分布结果设计了立柱的基本外形。根据立柱的外形特点,对比了5种不同类型筋板形式的单元结构,发现W形式的筋板结构材料消耗较少同时综合力学性能较优。选择W形式的筋板对立柱的外形结构进行布局及尺寸优化,得到了最终的立柱结构形式。对新的立柱结构进行有限元分析,结果表明,新设计立柱结构的质量减轻了8.3%,并且其静、动力学性能得到了不同程度的改善,实现了立柱结构的轻量化设计。
拓扑优化;筋板;立柱结构;轻量化设计
0 引言
随着机床控制系统集成化程度、精度越来越高,机床零部件的机械结构已向着高度集成、低功少材、高可靠性的方向发展,机床结构件的轻量化设计已成为机床研究领域的一个热点。立柱作为机床中关键的受力构件,重量较大,并且其强度、刚度的好坏将直接影响到机床的精度和寿命[1-2]。如何在保证立柱静、动力学性能的前提下实现结构的减重是目前立柱结构轻量化研究的重点方向。
结构的轻量化设计可归结为一个优化问题,通常以结构件的质量为目标,结构静态或动态性能为约束条件,寻求质量的最小化。有限元法能够大大缩短结构优化设计的周期并省去一些不必要的常规性实验,在机床结构件的优化应用中已十分广泛[3-5]。拓扑优化技术作为一种新颖的结构优化设计方法,在理论上往往能够大幅提高结构的某一性能。但由于拓扑优化结果通常难以直接应用于工程中,使得这种方法在机床结构件优化的实际应用中难以推广[6-7]。机床结构件设置筋板与加强肋是提高其承载刚度并减少质量的有效措施,并且大多筋板形式制造工艺性较好,因此机床零部件结构广泛采用不同种类的筋板形式[8-9]。尺寸优化作为一种有效地结构优化手段,在机床结构件的优化设计应用中已日益广泛[10-11]。
本文以某卧式加工中心的立柱为轻量化研究对象,对其结构进行重新设计。采用拓扑优化技术得到了立柱结构的基本外形,并在此基础上进行筋板的选型、布局及尺寸优化。分析结果表明,新设计的立柱结构质量得到了减轻,并且其静、动力学性能也得到了改善。
1 立柱的有限元分析
1.1 机床结构介绍
本文所研究的立柱来源于某卧式加工中心,如图1所示,该机床带有托盘交换机构,可实现工作台的交替加工。滑鞍及主轴箱等零部件沿立柱滑动导轨(X方向)的运动行程为1000mm,主轴箱沿滑鞍导轨(Y方向)的运动行程为900mm,工作台沿床身导轨(Z方向)的运动行程为900mm。整机质量为14179kg,立柱质量为4019.8kg。

图1 某卧式加工中心整机机械结构图
该机床立柱如图2所示,其内部结构可看作由纵横交错的“井”字形筋板组成,在筋板之间开有矩形的出砂孔。立柱整体为对称的结构形式,在顶部、前段及两侧留有凸台与其它零部件进行连接。

图2 立柱内部结构图
1.2 立柱的静、动力学分析
立柱主要的受力来源为机床加工时产生的切削力、立柱前端零部件的重力及其自身的重力作用。计算滑鞍及主轴箱等零部件在立柱导轨两端及中间位置处立柱的静力变形值,结果如表1所示。

表1 三个位置处立柱的静力变形值
对立柱进行模态分析,由于结构的低阶固有频率对其性能影响较大,所以这里只分析立柱的前三阶固有频率。立柱的振型如图3所示,前三阶振型均表现为结构的整体振动,且都为单一的摆动或扭转振型,没有局部振型出现,这说明结构整体形式较为合理。
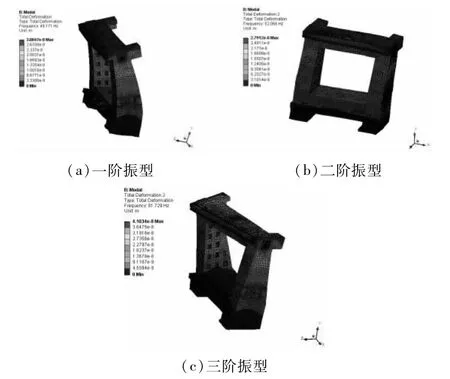
图3 立柱前三阶振型
2 立柱拓扑优化及外形设计
2.1 变密度法拓扑优化
结构的拓扑优化可看作是材料在设计空间中的分布问题。变密度法以结构每个单元的材料密度为设计变量,使其在0~1之间连续变化(0表示没有材料,1表示有材料),通过对中间的材料密度单元进行惩罚,使中间密度单元趋于0或1,最终得到结构的拓扑优化结果。
立柱的拓扑优化模型如图4所示,将立柱与其它零部件没有装配关系的区域作为优化区域(为了方便力的施加,需将三个位置处的滑块均表示出来)。以三个位置处立柱的加权柔度能最小为目标函数,同时对优化后的立柱结构前三阶固有频率与体积分数进行约束。

图4 立柱拓扑优化模型
利用HyperWorks软件中的OptiStruct模块对立柱的拓扑优化进行计算,得到图5的收敛曲线。从图中可看出,目标函数迭代到27次时收敛,此时一阶固有频率在55Hz左右,大于立柱原始结构的49.17Hz。图6是迭代到27次时去除密度小于0.3的材料分布结果。
首辅不仅仅是排名居首的阁臣,他还拥有至关重要的票拟权。然而,首辅在阁臣中不一定权力最大。例如,“时李时为首辅,政多自言出。”[2](卷196,夏言传)“(翟)銮 以 资 地 居 其 上,权 远 出(严)嵩下。”[2](卷193,翟銮传)“阶虽为首辅,而拱自以帝旧臣,数与之抗,朴复助之,阶渐不能堪。”[2](卷213,高拱传)“及高拱再入直,凌春芳出其上,春芳不能与争,谨自饬而已。”[2](卷193,李春芳传)

图5 目标函数及一阶频率收敛曲线

图6 去除材料密度为0.3以下的拓扑优化结果
2.2 立柱外形的设计
从图6可看出,立柱拓扑优化后的材料分布极不规则,这难以直接应用,但从外观上看,其外形结构可以基本确定下来,将立柱的外形设计为图7所示的结构形式。根据材料分布情况,在不改变立柱装配关系的情况下,顶端设计为一斜边形式,底部中间为直边,两端为圆弧形状,在中上部与底部开有减重孔。为了方便制造,将立柱的内侧面去除,并在此基础上添加筋板结构进行布局。
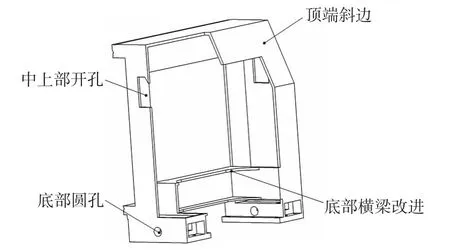
图7 立柱外形的设计
3 筋板的选型、布局及优化
3.1 筋板形式的选择
根据新设计立柱的外形结构特点(一面开口,三面封闭),在相同外形及筋板厚度的前提下,对比图8这5类常见筋板形式的单元结构综合力学性能。

图8 5类筋板形式
筋板结构的有限元模型如图9所示,分别分析5种结构在受压、弯、摆、扭这四种工况下的变形情况。

图9 筋板微结构有限元模型
考虑材料的影响,首先定义两个参数:

式(1)表示结构单位体积的刚度值,Kv值越大,表示结构材料消耗越少同时刚度越大;式(2)表示结构单位体积的固有频率值,ωv值越高,表示结构材料消耗越少同时固有频率越高,结构的动态性能也越好。

表2 Kv值计算结果

表3 ωv值计算结果
3.2 W形式筋板的布局与优化
W形筋板的布局主要集中在立柱的顶端、底部及两侧。立柱内部顶端、底部及两侧其截面均为矩形,根据截面的尺寸,将筋板布置为图10所示的形式。顶端的拓扑结果删除材料较多,这里将布置4块W形筋板,筋板左右及上下采用对称形式。立柱侧面根据截面的长、宽尺寸,设置5块W筋板,各筋板上下对称。底部拓扑优化结果保留的材料较多,这里共设置8块筋板,筋板左右及上下也将保持对称性。
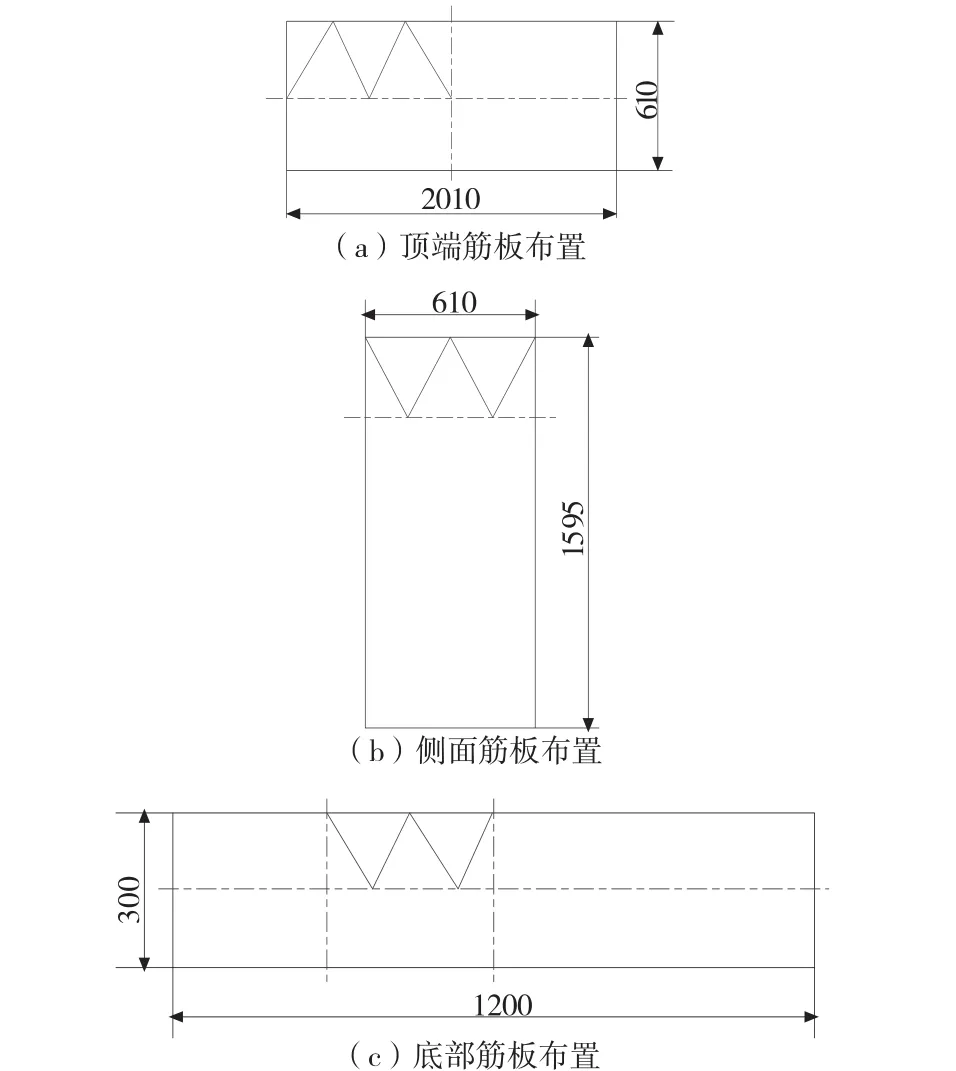
图10 立柱结构内部W形筋板布置示意图
由于立柱顶端、底部及两侧的筋板都采用左右或上下对称的形式,所以优化时只需对单个W形筋板优化即可。W形筋板可看做两个V字形筋板的组合,通过控制筋板之间的角度可实现立柱结构的优化。如图11所示,为了防止相邻筋板之间角度过小而难以制造,控制相邻筋板之间的角度均大于20°,每个W形筋板只需两个角度参数便确定其位置。角度参数与立柱一阶固有频率的关系曲线如图12所示,表4是最终的角度优化结果。根据角度值得到最终的立柱结构,如图13所示。


图11 W形筋板角度参数示意图

图12 W形筋板角度优化

表4 筋板角度优化结果

图13 新设计的立柱结构
4 立柱新结构的分析
对新设计的立柱结构进行静力学分析与模态分析,与原始立柱结构的数据对比结果如表5所示。从表中可看出,新设计的立柱结构质量降低了333kg,并且在三个位置处立柱的静力变形值均得到了减小,这可以保证立柱的刚度不会降低。同时,立柱的前三阶固有频率均得到了升高,较好的保证了立柱的动态性能。

表5 新立柱与原始立柱对比结果
综上所述,新设计的立柱较好地保证了结构的静、动力学性能,同时质量下降了8.3%,实现了结构的轻量化设计。
5 结论
(1)拓扑优化的结构难以直接应用,但根据拓扑优化结果的材料分布情况可设计出结构较优的基本外形。
(2)W形筋板结构具有较好的静、动力学性能,可应用于其它同类型机床结构件的轻量化设计当中。
(3)结合拓扑优化与筋板形式布局的机床结构件设计方法能够实现零件的轻量化,并改善结构的静、动力学性能。
[1]童忠钴,张杰.加工中心立柱床身结合面动态特性研究及参数识别[J].振动与冲击1999,2(3):13-19.
[2]Talaslidis D G,Manolis G D.Risk analysis of industrial structure under extreme transient loads[J].Soil Dynamics and Earthquake Engineering,2004,24(4):435-448.
[3]辛志杰,徐燕申,满佳,等.基于有限元分析的数控铣齿机立柱动静态设计[J].中北大学学报,2006,27(6):484-486.
[4]杨勇,张为民,李鹏忠.基于动态灵敏度分析的数控机床床身结构优化设计[J].机械设计,2011,28(9):49-52.
[5]章婷.基于有限元法的锻压机床身结构优化设计[J].锻压技术,2010,35(6):74-78.
[6]饶柳生,侯亮,潘勇军.基于拓扑优化的机床立柱筋板改进[J].机械设计与研究,2010,26(1):87-92.
[7]VHT800立式车铣加工中心立柱结构静动态优化及轻量化设计[J].组合机床及自动化加工技术,2011(3):12-15.
[8]孔杰.钢轨焊缝磨床床身动态特性分析及优化[J].湖南文理学院学报,2014,26(1):46-49.
[9]伍建国,陈新,毛海军,等.内圆磨床床身设计参数的灵敏度分析及动态设计[J].南京航空航天大学学报,2002,34(6):545-546.
[10]郭垒,张辉,叶佩青,等.基于灵敏度分析的机床轻量化设计[J].清华大学学报,2011,51(6):846-850.
[11]邢跷辉,王洪川,王贵飞,等.基于灵敏度分析的数控机床床身尺寸优化设计[J].组合机床及自动化加工技术,2013(11):6-7.
(编辑 赵蓉)
Lightweight Design of Column Structure Based on Topology Optimization and Reinforcing Rib Layout
LIU Cheng-ying1a,1b,TAN Feng2,WANG Li-ping1a,1b
(1a.Department of Mechanical Engineering,b.Beijing Key Lab of Precision/Ultra-precision Manufacturing E-quipments and Control,Tsinghua University,Beijing 100084,China;2.The School of Mechatronics Engineering,University of Electronic and Technology of China,Chengdu 611731,China)
In order to achieve the lightweight design of machine tool column,topology optimization of its structure is researched.From material distribution results of topology optimization,the basic shape of column structure is designed.According to the characteristics of the column basic shape,5 unit structures with different types of reinforcing ribs are compared.The structure with“W”reinforcing rib has well mechanical performance and consumes less materials.The“W”reinforcing rib is distributed and optimized on the basic shape of column structure,and the column is finally designed.Finite element analysis results demonstrate that the mass of the new designed column structure is reduced by 8.3%.Its static/dynamic performance has been improved with different degrees,and the lightweight design of column structure is achieved.
topology optimization;reinforcing rib;column structure;lightweight design
TH113;TG506
A
1001-2265(2015)04-0001-04 DOI:10.13462/j.cnki.mmtamt.2015.04.001
2014-08-01
“十二五”国家科技支撑计划项目(2012BAF01B02);国家科技重大专项(2013ZX04001-021)
刘成颖(1960—),女,辽宁大连人,清华大学副教授,研究方向为超精密加工工艺与装备、精密驱动与控制、CAD/CAM/CAPP,(E-mail)liucy@tsinghua.edu.cn;通讯作者:谭锋(1989—),男,贵州人,电子科技大学硕士研究生,研究方向为机床结构件优化与数字化设计,(E -mail)csutanfeng@163.com。
