介观尺度不均匀对反射系数的影响

李依佳，陈学华，许迪，甘子塬

（1.成都理工大学地球物理学院，四川成都610059；2.成都理工大学沉积地质研究院，四川成都610059）

介观尺度不均匀对反射系数的影响

李依佳1，陈学华1，许迪1，甘子塬2

（1.成都理工大学地球物理学院，四川成都610059；2.成都理工大学沉积地质研究院，四川成都610059）

介观尺度介于地震波长尺度及孔隙颗粒尺度间，地震波传过介观尺度不均匀介质时层间的应力差会引起流体流动，摩擦力使动能向热能转化产生衰减。White层流模型［1］是介观尺度的不饱和模型，该模型中两种饱和介质薄层周期交替。计算了地震频带上纵波穿过饱气层、饱水层周期出现模型的相速度Vp（ω）和品质因子Q（ω）；建立无衰减对比模型以计算对反射系数的影响。结果显示纵波入射不饱和层时，反射系数随频率变化明显，尤其是在低频处的衰减峰值附近。

介观尺度；衰减；反射系数

地震波在传播路径中产生能量损失的衰减机制大概有吸收、散射及绕射等。吸收相关的能量损失与传播介质温度的增加及弛豫现象有关。散射及绕射导致波的传播方向改变。在本文研究中，不考虑几何扩散、多重散射等造成的明显衰减，仅仅关注内在衰减过程-地震波能量由于孔隙流体的存在转化为热能。理解部分饱和孔隙岩石弹性波传播的物理性质对油气储层的勘探很重要。解开内在的影响可以成为定量解释测井及地震数据的有效方式，比如声波测井及延时地震研究中的真振幅合成地震记录。地下岩石物理性质控制的内在衰减可以提供地层学、岩石学、目标区域流体含量等有价值的信息。

Biot于1962年提出了宏观衰减机制。Dvorkin于1995年提出了微观尺度上的流体流动机制即局域流或喷流衰减机制。Pride（2004）由理论实验探讨了岩性变化、流体饱和度变化和微观尺度各向异性对衰减的影响，得出微观尺度衰减不足以解释地震频带衰减，而岩性、流体饱和度变化导致介观不均匀造成的衰减很容易解释，证实介观不均匀引起的孔隙流体流动是地震频带范围内衰减的主因。

1　周期层状模型及其解析解

孔隙介质不均匀的主要分为岩石骨架不均匀，所含非饱和流体分布不均匀，本文主要探讨后者。White于1975年提出了层流模型，在一维层流模型中，部分饱和储层可以等效为两种介质薄层（L1及L2）周期交替的表征体元（REV）（见图1）。

图1　周期层状介质及表征体元Fig.1 Alternating layered media and representative elementary volume

该模型随频率变化的相速度及衰减由REV的等效体积模量E计算：

由White模型解析解［2］，式中E和平均密度由式（3）～（7）公式计算。下标1、2代表饱水层、饱气层，式（4）～式（7）省略下标。

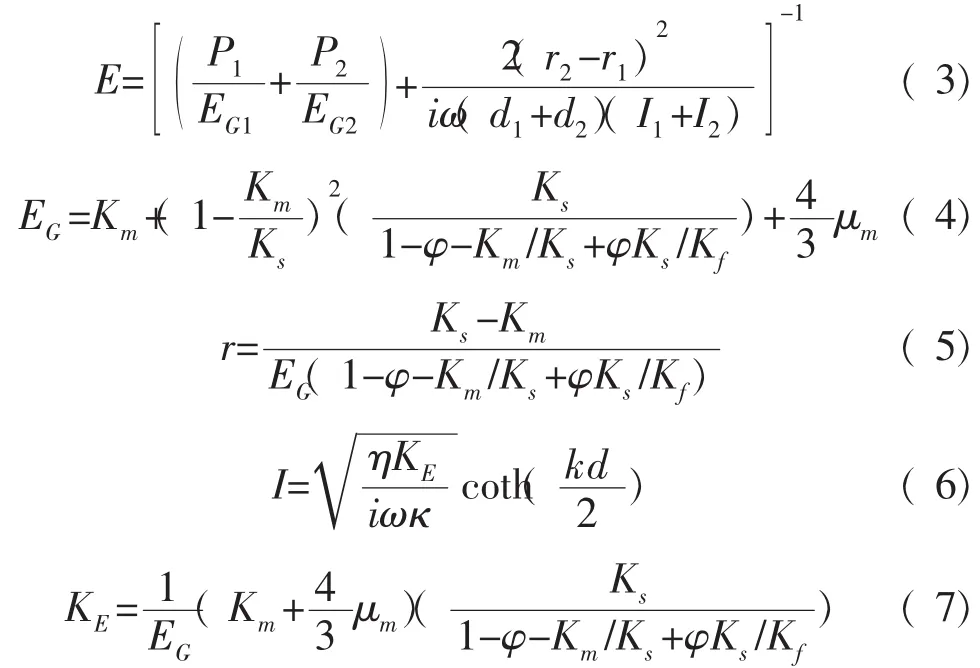
式中：脚标s、m、f分别表示岩石体、岩石骨架及流体，K及μ代表对应的体积模量与剪切模量；EG为Gassmann模量，KE为有效模量。d1与d2在本文中分别为REV中L1、L2的厚度。φ为孔隙度，κ为渗透率，η为黏度，ω为角频率。

划分弛豫与非弛豫阶段的过渡频率［3］见式（8），该频率处相速度变化最大且达到衰减峰值。

其中脚标1代表水层。由式（8）可见，随着流体黏度增加、渗透率降低，介观衰减机制的过渡频率趋于低频，这个趋势是与Biot弛豫机制相反的。

设L1、L2厚度分别为0.4 m、0.1 m，孔隙度分别为0.1及0.4，渗透率分别为150 mD及2 000 mD，其余岩石参数相同（见表1），L1、L2各含水、气参数（见表2）。代入式（1）～式（7）中计算孔隙度频变衰减及相速度。

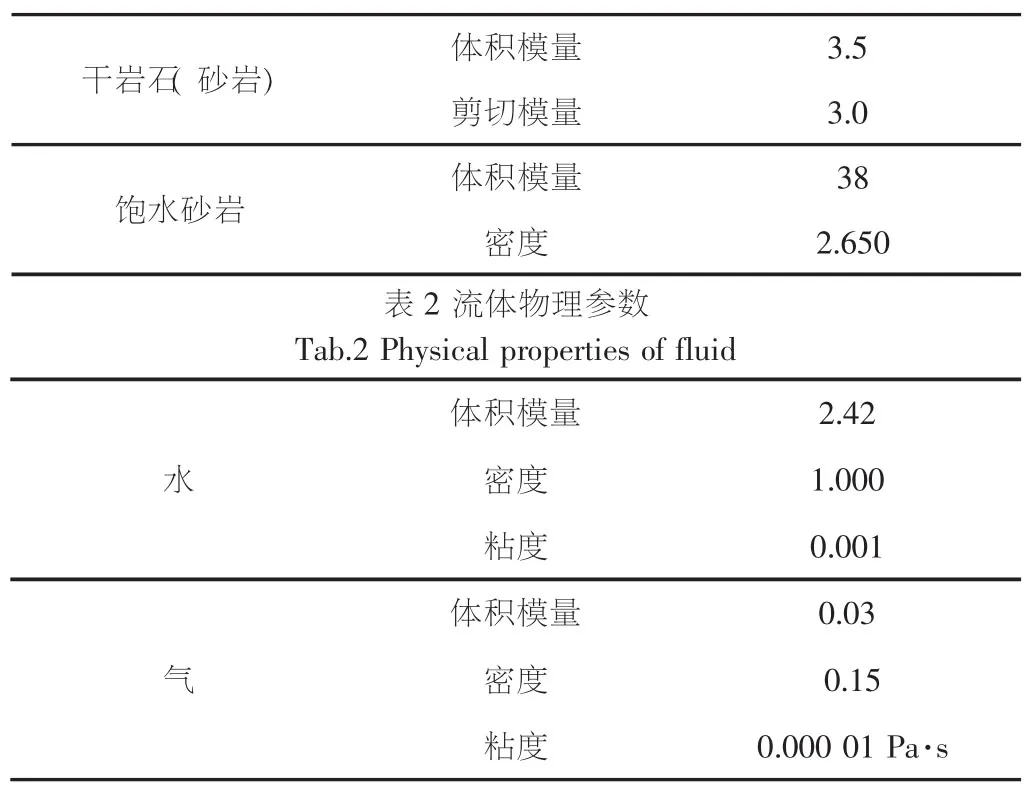
表1　砂岩物理参数Tab.1 Physical properties of sandstone

图2　频变气水交替层状模型的衰减系数曲线及相速度曲线Fig.2 Frequency-dependent attenuation coefficient（a）and phase velocity（b）

由图2可见，地震频段衰减系数1/Q随着频率增大到峰值后开始衰减，在低频正比于而高频正比于［4］，相速度变化最大处对应衰减系数曲线峰值频率。

2　衰减对反射系数的影响

纵波由弹性介质垂直入射目标介质的反射系数［5］为：

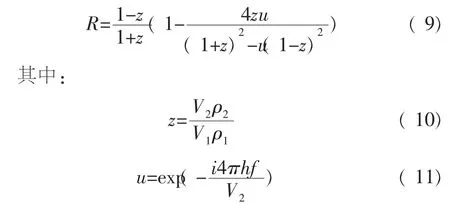
上式中的z为阻抗比，f为频率，h为层2的厚度。脚标1代表弹性背景层，脚标2代表目标层，波从层1垂直入射层2。层1速度V1若目标层使用White层流模型，则层2的速度V2为复速度（见式（12），式中i为虚数）；若目标层为弹性层，则V2使用前一节中的相速度。由式（9）可以得到由一系列薄层组合成的地层的总反射系数。随着波长的增大或层厚的减小会产生调谐效应，调谐频率ft见式（13），Vp2为周期层相速度。

设La层为层流模型组成的衰减层，Lb层为对比弹性层（相速度等于f/fq=1时La的相速度），Lc为背景弹性介质（相速度等于f/fq=0.75时La的相速度），Lb及Lc的密度都等于La的体平均密度。La嵌入Lc，作为对比项时Lb替代La嵌入Lc。

当频率f=0.78ft时，三种介质的阻抗对比（见图3（a）），Lb、Lc阻抗为定值，Lc阻抗大于Lb，La阻抗曲线与上节中速度曲线趋势相似，在0.75≤f/fq≤1时La的阻抗大于Lb，但是La的上下层波阻抗差小于Lb，预测该段Lb反射系数大于La；反射系数绝对值（见图2（b）），La恒大于Lb。图3（a）与（b）所得预测结论矛盾，可以解释该现象的原因是0.75≤f/fq≤1频段介质存在高衰减。

图3　La、Lb、Lc阻抗图（a）与反射系数绝对值图（b）Fig.3 Impedance of La、Lb and Lc（a），and absolute value of reflection coefficient（b）

3　结论

流体不饱和会引起高衰减及速度频散，可以得到依赖频率的复阻抗。纵波入射单层厚度小于波长的气-水不饱和层状介质时，产生的频变衰减对反射系数有很大影响，在过渡频率趋于低频附近表现尤其明显。加深对依赖频率的反射系数的理解有助于解释地震数据及研究从地震数据中识别流体属性的新方法。

［1］White，J.E.，N.G.Mikhaylova，and F.M.Lyakhovitskiy，1975，Low-frequency seismic waves in fluid saturated layered rocks∶Izvestiya，Academy of Sciences，USSR.Physics of the Solid Earth，11，654-659.

［2］Carcione，J.E.M.and S.Picotti，P-wave seismic attenuation by slow-wave diffusion∶Effects of inhomogeneous rock properties［J］.Geophysics，2006，71（3）：1-8.

［3］Dutta，N.C.，and A.J.Seriff，1979，On White's model of attenuation in rocks with partial saturation∶Geophysics，44，1806-1812.

［4］Muller，T.M.and B.Gurevich，Wave-induced fluid flow in random porous media∶Attenuation and dispersion of elastic waves［J］.The Journal of the Acoustical Society of America，2005，117：2732.

［5］Brekhovskikh，L.M.，1980，Waves in layered media∶Academic Press，Inc.

Influence of mesoscopic heterogeneity on reflection coefficient

LI Yijia1，CHEN Xuehua1，XU Di1，GAN Ziyuan2
（1.Geophysical Institute，Chengdu University of Technology，Chengdu Sichuan 610059，China；2.Institute of Sedimentary Geology，Chengdu University of Technology，Chengdu Sichuan 610059，China）

Mesoscopic scale is larger than grain and smaller than wavelength.The pressure difference between different fluids induced fluid flow when seismic wave penetrate the mesoscopic inhomogeneous media.The cause of attenuation is the friction which transfer kinetic energy to heat.White's layered fluid model is a kind of mesoscopic-scale partially saturated model with two periodically alternating saturated layers.This paper computes the phase velocity Vp（ω）and quality factor Q（ω）of water-gas saturation layered model.A comparison is modeled to research the attenuation effect on reflection coefficient.The result show that the reflection coefficient of unsaturated layer changes significantly with frequency，especially near peak frequency of attenuation.

mesoscopic-scale；attenuation；reflection coefficient

10.3969/j.issn.1673-5285.2015.05.008

TE311

A

1673-5285（2015）05-0036-04

2015－03-27

国家自然科学基金项目，项目编号：41374134、四川省杰出青年科学基金，项目编号：2013JQ0011和成都理工大学优秀创新团队培育计划，项目编号：KYTD201410，联合资助。

李依佳，女（1992-），成都理工大学在读硕士研究生，研究方向为油气与矿产地球物理，邮箱：lyj2337721@gmail. com。