曲轴磨床切点跟踪运动三次样条逼近研究*

党志广，黄 艳，王鹏博，田 野

（1.中国科学院大学，北京 100049；2.中国科学院沈阳计算技术研究所，沈阳 110168；3.沈阳高精数控技术有限公司高精数控研究室，沈阳 110168）

曲轴磨床切点跟踪运动三次样条逼近研究*

党志广1，2，黄 艳2，3，王鹏博1，2，田 野3

（1.中国科学院大学，北京 100049；2.中国科学院沈阳计算技术研究所，沈阳 110168；3.沈阳高精数控技术有限公司高精数控研究室，沈阳 110168）

根据曲轴磨床切点跟踪运动的特点，文章阐述了建立切点跟踪数学模型的整个过程，并且提出用三次样条曲线对曲轴磨床切点跟踪运动过程中的轨迹点进行逼近的方法，演绎了曲轴磨床切点跟踪运动的三次样条曲线方程的推导过程。三次样条曲线函数具有一阶导数和二阶导数连续的特点，所以轨迹逼近拟合效果好，加工曲面整体光滑，符合曲轴零件型线轮廓要求。通过对比仿真实验结果证明，三次样条逼近算法能使磨削曲线整体平滑，并且逼近误差小。

曲轴磨床；切点跟踪；逼近误差

0 引言

曲轴作为船舶、机车和发电等设备内燃机上的关键零件，其加工质量与内燃机的耐磨损性、耐疲劳性、振动、噪声等性能密切相关，所以曲轴的性能将直接影响内燃机的整体性能。随着船舶、机车等制造业的快速发展、内燃机产品的更新换代，对大型曲轴的产量和质量都提出了更高的要求。切点跟踪磨削法作为一种全新的集中式工序的曲轴磨削方法，克服了传统曲轴类零件磨削方式的缺点，实现一次装夹就能依次完成对曲轴主轴颈和各连杆颈的磨削，排除了因工件两次装夹而产生的定位误差，更容易保证加工精度，大大减少了辅助时间，降低了设备、厂房的投资。开展对该方法的研究工作，能为今后开发设计高精磨床设备提供可靠的理论根据，这对于促进机械制造业的发展和制造加工水平的提高，具有十分重要的理论意义和较高的实用价值。

工件的精度和加工的效率受轨迹插补控制的精度和速度的制约，所以本文提出用三次样条曲线对曲轴磨床切点跟踪运动过程中的轨迹点进行逼近的方法，这种方法和传统的等误差直线逼近方法相比提高了逼近精度和曲线的光滑性，更契合工件加工过程中要求的光顺性原则。研究内容包括以下几部分：首先根据切点跟踪磨削特点，建立磨削数学模型；第二部分主要内容在数学模型的基础上提出三次样条曲线，并且给出了曲线的具体求解过程；最后一部分通过Matlab进行仿真实现切点跟踪磨削的三次样条曲线，并通过实验对比证明了三次样条曲线磨削的精度更高，工件加工精度更高。

1 切点跟踪中磨削点运动方程

在切点跟踪磨削运动中，曲轴连杆颈轮廓是由砂轮跟随曲轴的回转运动，在磨削过程中始终与连杆颈保持相切而形成的。曲轴连杆颈切点跟踪磨削运动模型如图1所示。

图1 曲轴切点跟踪磨削运动示意图

由上图可知，曲轴连杆颈绕主轴颈中心O旋转，砂轮沿X轴做往复跟踪运动，在运动过程中始终与曲轴连杆颈保持相切以实现曲轴连杆颈的切点跟踪磨削，磨削点坐标的轨迹方程为：

上式中R为曲轴连杆颈偏心距，Rw为曲轴连杆颈半径，Rs为砂轮半径，（Xi，Yi）为磨削点相对曲轴回转中心O的坐标，Os为砂轮中心，Ow为连杆颈中心，α为OwO与OsO的夹角，β为OwOs与OsO的夹角。

由图1中的几何关系可以推导出曲轴连杆颈切点跟踪磨削过程中砂轮中心与曲轴转角之间的运动方程，如下式（4）所示。

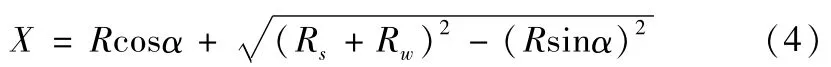
当主轴颈匀速转动时，可根据任一时刻的α值求得砂轮中心的位置坐标。当曲轴偏心距R=65mm、连杆颈直径Dw=79mm、砂轮半径Rs=299.12mm时，曲轴连杆颈切点跟踪磨削过程中砂轮中心的运动轨迹如图2所示。图中的曲线是加工过程中曲轴连杆颈和砂轮相切时砂轮中心的运动曲线，这也为第三部分三次样条曲线模拟仿真绘制的曲线提供了对比依据。

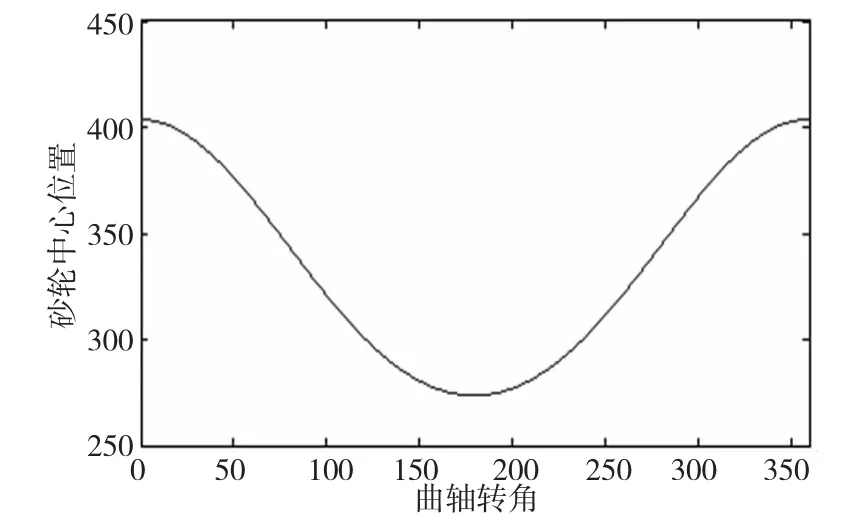
图2 砂轮中心随曲轴转动的运动轨迹

2 三次样条曲线逼近算法

2.1 三次样条曲线定义及解法

三次样条曲线的数学定义：在平面区间上有n+1个点（αi，Xi），其中i=0，1，2，3…n。假定a=α0＜α1＜α2… ＜αn=b，若函数X（α）满足条件：

2.2 曲轴切点跟踪运动的三次样条曲线逼近

基于以上分析，了解到三次样条函数曲线，具有一阶导数和二阶导数连续的特点，使得曲轴磨削运动轨迹的三次样条逼近的曲线整体光滑，所以提出曲轴磨削运动采用三次样条逼近。

根据曲轴切点跟踪磨削运动模型，可得曲轴转角α和砂轮架跟踪位移X的一系列离散点 （α0，X0），（α1，X1）…（αi，Xi）…（αn，Xn）。由2.1分析了解到只要求得μ，η的边界条件就可以得出三次样条曲线，通过分析曲轴切点跟踪运动可以得出 X（α0）'= X（αn）'=0，可以得出μ，η的边界条件式（12）。然后通过公式（7）、（8）、（9）、（10）可以得出三次样条曲线。

3 三次样条曲线仿真实验

根据三次样条曲线函数求解过程进行模拟仿真实验。选取偏心距R=65mm，连杆颈的直径Dw=79mm的曲轴为仿真对象，相关的仿真参数：砂轮半径Rs= 299.12mm，工件平均转速30r/min。

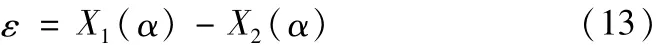
切点跟踪磨削运动轨迹采用三次样条函数进行曲线逼近，在等角度插值条件下根据公式（4）获取曲轴切点跟踪磨削运动轨迹曲线上的72组原始数据点，对其进行三次样条曲线逼近仿真实验。公式（13）给出了误差计算方法，X1（α）是三次样条曲线的公式（6）求出的值，X2（α）是切点跟踪模型曲线公式（4）所求出的值，工件磨削过程中逼近误差绝对值如图3所示。从图中可以看出起始点的误差比较大，而远离起始点的部分切点跟踪的逼近误差比较小。这是由于采用三次样条逼近切点跟踪磨削运动轨迹时，需要知道边界条件（起始点的一阶和二阶导数），而通常情况下边界点的一阶和二阶导数是通过临近点近似计算出来的。由于曲轴切点跟踪磨削运动轨迹的周期性特点，加工过程中可以通过增加一个周期来避免这样的误差。

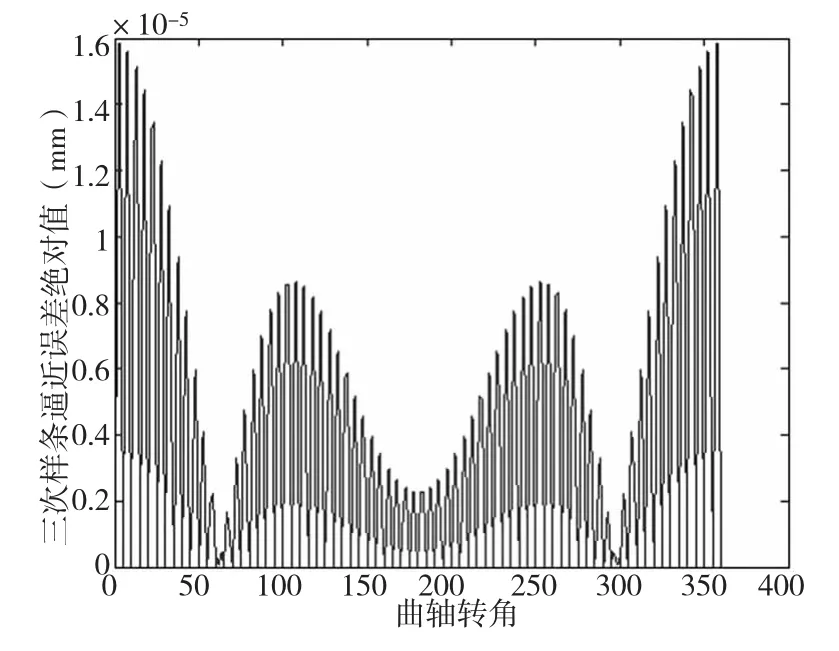
图3 三次样条曲线逼近误差绝对值

表1是等误差直线逼近在不同期望精度的逼近段数，误差逼近段数是公式（13）中误差ε大于给定的期望精度时，重新计算一段新的曲线，实验中完成曲线磨削一周需要的最小段数就是误差逼近段数，表1给出了不同精度下两种方案的逼近段数。从表1中可以看出，在相同数量级10-5误差情况下，三次样条曲线逼近只需要分407个逼近段数，而等误差直线逼近则需要643段。由此可以得出：在相同的误差要求下，三次样条曲线与传统的等误差直线逼近相比逼近段数要的多。因此三次样条曲线算法在程序中需要保存的离散点的数据量就会少很多，这在很大程度上减轻了数控程序的负担。

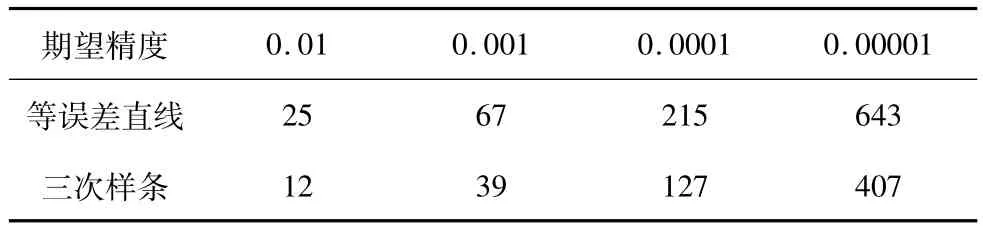
表1 等误差直线和三次样条逼近段数对比

图4和图5分别是等误差直线逼近和三次样条曲线逼近算法在曲轴磨削一周形成的曲线。从图中可以很清晰的发现三次样条曲线与原曲线图2基本一致，曲线比较平滑，而等误差直线逼近曲线整体很不平滑且有很多折点。以上两点说明了三次样条曲线在切点跟踪磨削过程的优势，这对于设计大型高精度数控机床具有很好的理论指导意义。

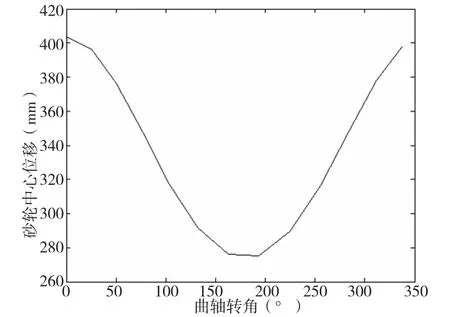
图4 等误差直线拟合曲线

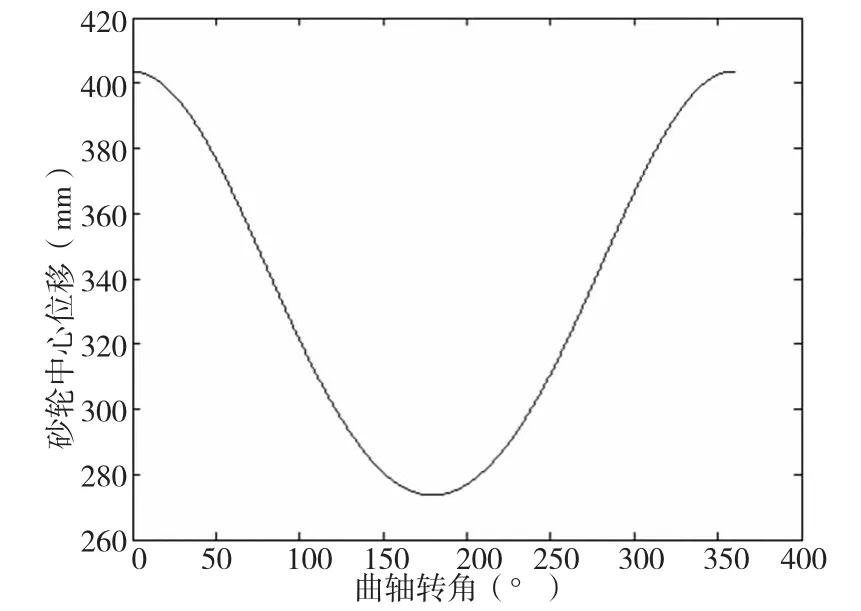
图5 三次样条拟合曲线

4 结束语

本文提出用三次样条曲线对曲轴磨床切点跟踪运动过程中的轨迹点进行逼近的方法。通过仿真实验发现，三次样条曲线逼近明显优于等误差直线逼近，为曲轴切点跟踪提供了一种高效的控制方法。

［1］龚时华.凸轮轴高速磨削加工控制系统关键技术［D］.武汉：华中科技大学，2008.

［2］张智斌.曲轴磨床切点跟踪运动分段多项式逼近研究［J］.精密制造与自动化，2013（3）：19-25.

［3］汪学栋，房小艳.切点跟踪曲轴磨床磨削力的计算公式分析［J］.精密制造与自动化，2012（3）：17-19.

［4］张晓波.三次样条曲线在道路线形设计中的应用［J］.铁道勘测与设计，2007（1）：15-17.

［5］TFujiwara，STsukamoto，MMiyagawa.Analysis of the Grinding Mechanism with Wheel Head Oscillating Type CNC Crankshaft Pin Grinding［J］.Key Engineering Materials，2005，（291-292）：163-168.

［6］吴钢华.曲轴非圆磨削轨迹控制关键技术研究［D］.上海：上海大学，2006.

［7］沈南燕.曲轴非圆磨削中的误差分析及补偿方法研究［D］.上海：上海大学，2007.

［8］李勇.影响数控凸轮轴磨削加工精度若干因素的研究［D］.武汉：华中科技大学，2004.

［9］周杰，刘学平，段广洪，等.曲轴切点跟踪磨削法控制误差分析研究［J］.机械设计与制造，2012（12）：7-9.

［10］许小勇，钟太勇.三次样条插值函数的构造与Matlab实现［J］.自动测量与控制，2006（11）：76-78.

［11］陈露.基于特征性质的三次B样条拟合算法［D］.大连：大连理工大学，2009.

（编辑 赵蓉）

The Research on the Crankshaft Tangential Point Tracing Grinding Based on Cubic Spline

DANG Zhi-guang1，2，HUANG Yan2，3，WANG Peng-bo1，2，TIAN Ye3
（1.University of Chinese Academy of Sciences，Beijing 100049，China；2.Shenyang Institute of Computing Technology，Chinese Academy of Sciences，Shenyang 110168，China）

According to the characteristics of the crankshaft grinder tangential point tracking movement，this paper explained the process of making the mathematical model，and proposed the method based on the cubic spline curve to approach the track points which are generated to track the movement of the crankshaft grinder cut-off point.At the same time，the process of deriving the cubic spline curve that track the movement of the crankshaft grinder cut point is illustrated in the paper.Cubic spline function has the continuous features of the first and second derivative，so the fitting effect is good and the cutting surface is smooth，which conforms the profile requirements of the crankshaft parts.The results in the simulation show that the approximation algorithm of the cubic spline enables the curve smooth overall，and the approximation error is small.

crankshaft grinder；tangential point tracing；approaching error

TH16；TG506

A

1001-2265（2015）10-0005-03 DOI：10.13462/j.cnki.mmtamt.2015.10.002

2014-11-28；

2015-01-21

"高档数控机床与基础制造装备"国家科技重大专项—基于二次开发平台的专用数控系统开发与应用（2013ZX04007-011）

党志广（1988—），女，河南课河人，中国科学院大学硕士研究生，研究方向为数控技术，（E-mail）dzg0123@126.com。