物联网感知层多Sink节点关联算法研究*

王华东，王大羽

（周口师范学院计算机科学与技术学院，河南周口 466001）

物联网感知层多Sink节点关联算法研究*

王华东，王大羽

（周口师范学院计算机科学与技术学院，河南周口 466001）

针对大规模无线传感器网络采用单一的Sink节点容易造成网络“能量空洞”效应，而多Sink节点数量和位置的合理部署能有效延长无线传感器网络寿命、控制网络成本，同时多Sink节点数量和位置是一个NP--难问题，因此提出新颖的萤火虫算法对多Sink节点布局模型问题进行求解计算，并对算法的计算精度、效率进行了分析。通过理论分析和仿真验证表明，结果表明文中提出基于萤火虫算法的多Sink节点布局模型与随机分布，基于遗传算法、蚁群算法的多Sink节点部署算法相比，能够有效降低无线传感器网络的能量消耗，减少端到端网络延时，降低网络部署成本，提高网络服务效率，延长网络的生存期。

物联网；感知层；多Sink节点

0 引言

随着传感器技术、计算机技术、网络技术、无线通信技术的迅猛发展，许多专家学者投入其中，无线传感器网络技术随之得到了快速地进步［1］。对于规模较大的无线传感器网络，数据传递给Sink节点需要经历多跳通信，每个感知节点都具有采集信息，同时承担路由转发的功能，要传递大量的信息到源节点，而感知节点能量的消耗往往与通信的距离是成正相关关系［2］。在无线传感器网络中合理分配Sink节点个数和部署位置，可以缩短传感器节点与Sink之间的传输距离，从而有效地减少通信中的能量损耗［3］。

许多专家学者对多Sink无线传感器网络路由协议进行了相关研究，相比于单一Sink路由协议，多Sink无线传感器网络路由协议具有更多的优点。刘强等［4］提出随机分布WSN中Sink节点部署研究，通过对节点合理部署提高网络效率，延长网络寿命；熊永平等［5］提出基于VSR的多Sink机会移动传感器网络的数据收集算法，提高了数据收集效率，提高了网络效率；袁甜甜等［6］针对路径最小剩余能量、路径最小平均链路质量和节点到Sink的跳数等因素，提出基于模糊综合评判的多Sink最优路由算法，该算法能延长网络生存期，提高数据包交付率。以上这些算法主要针对传感器网络规模不是很大，考虑更多的是节点自身剩余能量，而没有解决多Sink节点之间的协同与合作，或者算法的复杂度较大，开销也较大。因此考虑到感知节点的剩余能量、多跳跳数、传输距离等问题，本文从群智能启发式算法出发，提出基于萤火虫算法的多Sink节点部署问题，，有效的均衡了感知节点的能量消耗，延长了网络的使用寿命。

1 多Sink节点放置位置数学模型

Sink节点的布局情况与无线传感器的网络服务性能紧密相连，即无线传感器网络中的Sink节点与感知节点之间存在服务与被服务的关系［7］。无线通信网络链路的可靠性、服务效率与服务点、被服务点之间的距离紧密相连，因此通过缩短Sink节点与传感器节点之间距离，可以提高网络服务效率［8］。

在无线传感器网络上选取放置Sink节点个数及部署位置时，需要考虑以下几个问题：第一，评估放置Sink节点的能力，承担数据汇聚的能力；第二，对于每个普通传感器节点都必须有一个Sink为其提供相应服务；第三，每个普通传感器节点到其对应的Sink节点之间的延迟不能太大。Sink节点放置问题的优化目标就是如何优化放置的位置，使普通传感器节点到Sink节点之间的时间的最大延迟达到最小以及感知节点发送数据能耗最小，并满足Sink节点汇聚能力。我们把该问题称为（Multiple Sink Node Placement Problem，MSNPP）问题［9］。

给定一个图论形式的带权无向图无线传感器网络G=（V，E），其中V是所有传感器网络中感知节点集合；E是网络中边的集合（假如网络中两个感知节点信号连通，就可以连成一条边），边权表示节点之间通信连接权值，可定义为网络时延、信号强度大小等。定义w：V x V，e（0，），w（i，j）=w（j，i）。其中MSNPP数学模型定义为：普通感知节点集合D⊆V，F⊆V为无线传感器网络放置Sink集合，整数ui表示为传感网Sink节点i的汇聚能力，其中引入0-1变量，定义如下：

公式中path（i，j）表示普通感知节点j到其对应的Sink节点i所经过的最短路径，约束条件为：式（2）表示集合D中每个感知节点一定要分派给唯一的Sink节点。式（3）表示每个Sink节点到汇聚的感知采集节点不能超过自己的负载能力。式（4）考虑到网络成本问题，网络中Sink节点个数不能超过L个。式（5）表示普通感知节点分派到Sink节点一定是存在式（6）表示数学变量的取值范围。

本文通过萤火虫算法（Firefly algorithm，FA）对多Sink节点放置位置数学问题进行求解，寻找重点节点传输到多Sink节点的最短路径，下面第二小节简单阐述萤火虫算法。

2 萤火虫优化算法

自然界中，萤火虫可以通过感知一定范围内异性萤火虫的发光频率和强度来判断异性的吸引力，同时可以通过发光吸引猎物进而捕食猎物。由于萤火虫的发光强度会随着传播距离的变化而变化，英国剑桥大学X.S.Yang博士对萤火虫的发光行为进行抽象，于2007年提出了萤火虫算法，该算法是一种新的元启发式群智能算法。在求解函数优化问题时，萤火虫算法比PSO和GA更有效，并解决了很多工程问题［10］。

在萤火虫算法中，首先定义相关参数：萤火虫个体i，当前位置xi（k）和该位置对应的荧光素值li（k），同时对应一个目标函数值f（xi（k））。萤火虫在寻找食物过程中，首先会向周围的萤火虫传递相关信息，以目标函数值f（xi（k））为决策范围，之后决策范围会根据式（9）进行更新。

根据上述分析，GSO算法由四个阶段萤火虫种群初始化、荧光素更新、当前位置更新和萤火虫决策域更新组成。

3 GSO算法在多Sink节点部署应用

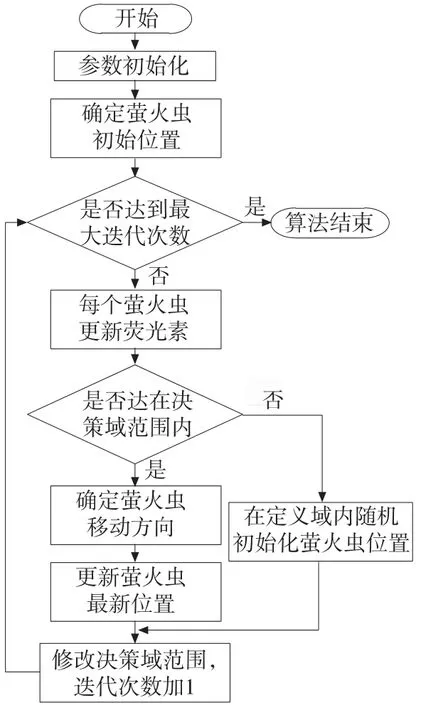
图1 基本人工萤火虫群优化算法流程图

具体的基于人工蜂群算法的多Sink节点部署MSNPP问题关联问题求解步骤如下：

（1）初始化种群。在某区域内随机抛洒传感器节点，并将每个传感器节点看成一个萤火虫，从而形成萤火虫群。在算法初始赋与随机播撒传感器节点中每个节点相同荧光素浓度。

（3）荧光素更新操作。对每个个体i按式（12）计算在第k代、位置xi（k）的适应度值，根据式（11）利用目标函数值来计算萤火虫i的荧光素值。

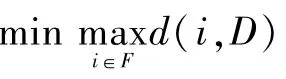
4 算法性能分析

为了验证本文提出基于萤火虫算法的多Sink节点的放置算法有效性及优越性，利用MATLAB仿真软件对随机撒播、遗传算法的多 Sink节点的放置算法［11］、蚁群算法的多Sink节点的放置算法［12］和本文算法进行仿真测试对比，仿真电脑配置为内存4G的奔腾处理器，仿真环境采用的是Matlab编程，版本为R2012b。在网络范围为200m x 200m的方形范围内随机部署100个感知终端节点和从1到10个变化的Sink节点，部署的节点遵循空间点泊松分别，实验室仿真环境参数如表1所示。

表1 实验仿真参数

仿真主要分为两部分：①从本文提出的算法本身出发，从Sink节点数量变化对最小平均距离关系、总跳数与Sink节点数之间的关系、路由空洞数与Sink节点数之间的关系、Sin节点数量与算法计算时间的关系等四个方面进行仿真试验。②对4种算法从网络寿命和端到端时延等两个方面对算法性能进行对比分析。

（1）Sink数量变化对最小平均距离的影响

在这里我们定义无线传感器网络最小距离L为每个感知节点发送信息到Sink节点之间的平均距离，用数学公式表述为：

其中S为网络最小总的加权距离，T为所有感知节点请求数之和。Sink节点的数量与最小平均距离的关系图如图2所示。

图2 Sink节点的数量与最小平均距离（m）的关系

一般而言，随着汇聚节点Sink数量的增多，感知节点的最小平均距离随之下降，网络的通信能力随之增强，可以通过增加Sink节点的数量来增强无线传感器网络的通信能力，但Sink节点不是越多越好，Sink节点越多，意味着网络的能耗在增加，网络寿命在下降。从图2可以看出，开始时最小平均距离为6.5左右，在Sink节点数量为4时下降到只有2.8左右，下降幅度超过了56.8%，说明增加Sink节点数量有效地减小了最小平均距离，增加了网络的通信能力。但当Sink节点增加到一定数量后，最小平均距离变化不大，逐步趋近平稳，当Sink节点增加到7时，对最小平均距离影响就很小了。

（2）总跳数与Sink节点数之间的关系

在200m x 200m的仿真区域中随机播撒50，100和150个普通的终端节点，同时设定网络的平均连通度分别对应5，15和18左右。为了验证总跳数与Sink节点数之间的影响关系，进行50次求取跳数的平均值。在仿真过程中，Sink节点与普通节点进行通信都使用MSDDGR协议，在进行数据传输时，网络中所有感知节点与任意一个Sink节点建立连接网络计算感知节点到Sink节点间的跳数。当Sink节点与周围节点建立路由连接时，网络进行一次轮询次数，记录网络中所有节点间总跳数与Sink节点数之间的关系，如图3所示。从图3可以看出，总的节点个数少时，总的跳数也相对较少，网络节点总数大时，总的跳数也相应地最多。同时本文使用的MSDDGR通信协议中感知节点的总跳数随Sink节点的增多而减少。当Sink节点个数增加到6之后，网络中总的跳数变化不大，曲线趋近平缓。

图3 总跳数与Sink数量对应关系

（3）路由空洞数与Sink节点数对应关系

同样地，对路由空洞个数的统计我们使用基于MSDDGR协议，在进行数据传输时，网络中所有感知节点与任意Sink建立连接，统计出现路由空洞情况，根据统计结果，绘制路由空洞数与Sink数量关系如图4所示。从图4可以看出，基于MSDDGR通信协议能有效提高网络通信能力，降低数据传输跳数，减少网络路由空洞数量，多个Sink的分散放置，使感知节点采集的数据只需发送给距离自己最近的Sink节点就可以，减少了网络的跳数，缩短了网络通信传输路程，降低了网络总跳数，路由空洞数随之减少。

图4 路由空洞数与sink节点数对应关系

（4）Sink节点数量与算法计算时间的关系

在大规模的无线传感器网络中，放置多个Sink节点可以减少数据传输距离和网络通信跳数，但会对网络部署计算耗时产生影响，Sink节点数量增加的同时也增加了网络部署计算数量量的加大，数据通信延时也会增大。Sink节点数量与本文提出的萤火虫多Sink放置算法计算时间的关系如图5所示。从图5的曲线走势可以看出，本文提出的基于萤火虫算法的Sink节点放置算法与部署所需的耗时呈线性增长关系，放置的Sink节点越多，部署所需计算时间相应也越长。通过启发式萤火虫算法的技术，布置合理的Sink节点数量和位置，能够适用于大规模的无线传感器网络多Sink节点放置问题。

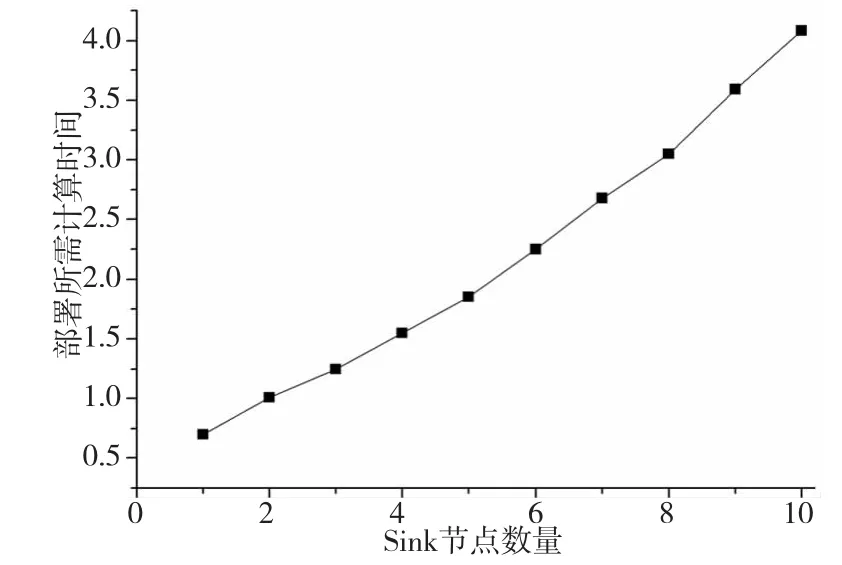
图5 Sink节点的数量与部署计算时间（s）的关系

（5）网络寿命

图6给出了随机分布、遗传算法的多Sink节点的放置算法、蚁群算法的多Sink节点的放置算法和本文提出的算法四种部署算法对网络寿命进行50次仿真，计算平均值后的网络寿命对比。从图6中可以看出，随着Sink节点放置数量的增加，网络的寿命都在随着增长，当Sink节点个数加到6个以后时，网络的寿命变化不大，网络寿命的曲线也趋近平缓，对网络寿命的影响不大。同时随机部署放置策略的无线传感网络寿命最短，远小于其它三种采用启发式算法的网络寿命时间，其中本文提出的算法比随机部署放置策略提高网络寿命25.3%，比基于遗传算法的放置策略的网络寿命提高12.1%，比蚁群算法的放置策略的网络寿命提高4.1%。

图6 不同部署算法下的网络寿命

（6）端到端网络时延

图7给出了四种算法的端到端网络时延对比，从图7来看，随着放置Sink节点个数的增加，端到端网络时延都在减小，但随机部署放置策略的端到端网络时延较大，遗传算法次之，蚁群算法较小，本文提出的萤火虫算法端到端网络时延最小。另外对这四种算法计算它们之间的均方值，本文提出算法比随机部署放置策略的端到端网络时延短0.05s，比遗传算法的放置策略的端到端网络时延短0.035s，比蚁群算法的放置策略的端到端网络时延短0.02s。从以上仿真结果可以看出，本文提出的启发式萤火虫算法，合理布置的Sink节点数量和位置，能够减少网络跳数、路由空洞数、端到端网络时延，延长网络寿命，能够适用于大规模的无线传感器网络多Sink节点放置问题。

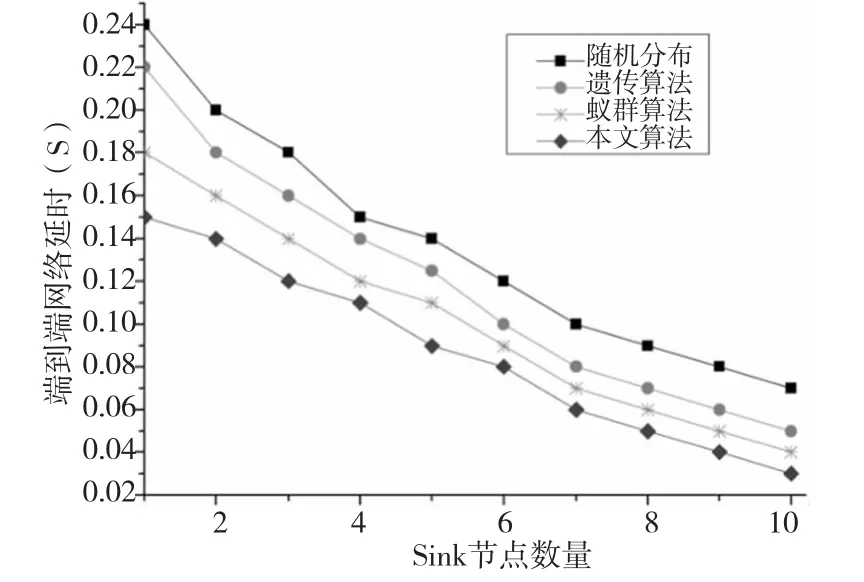
图7 不同算法下的端到端网络时延

5 结论

在大规模无线传感器网络监测环境中，采用单一的Sink节点容易使周围感知节点转发数据频繁而工作量巨大，导致自身能力迅速耗尽时网络失效，造成网络“空洞效应”。而多Sink节点数量和位置的合理部署能有效延长无线传感器网络寿命、控制网络成本，提出新颖的萤火虫算法对多Sink节点布局模型问题进行求解。通过理论分析和大量实验验证算法的有效性，实验表明该方法简单有效而具有实用性。本文提出的算法使多Sink节点进行最优部署，降低无线传感器网络的能量消耗，减少端到端网络延时，降低网络部署成本，提高网络服务效率，延长网络的生存期。

［1］Ming Ma，Yuanyuan Yang，Miao Zhao.Tour Planning for Mobile Data-Gathering Mechanisms in Wireless Sensor Networks［J］.IEEE Transactions on Vehicular Technology，2013，62（4）：1472-1483.

［2］Joohwan Kim，Xiaojun Lin，Shroff N B，et al.Minimizing Delay and Maximizing Lifetime for Wireless Sensor Networks With Anycast［J］.IEEE/ACM Transactions on Networking，2010，18（2）：515-528.

［3］梁小晓，韦崇岗，乐英高，等.基于小波神经网络的WSN目标识别设计［J］.计算机测量与控制，2013，21（9）：2550-2553.

［4］梁小晓，韦崇岗.基于人工蜂群算法的物联网数据融合技术研究［J］.组合机床与自动化加工技术，2013（5）：5-8.

［5］熊永平，孙利民，马建，等.VSR：多sink机会移动传感器网络的数据收集［J］.计算机研究与发展，2010，47（8）：1450-1458.

［6］袁甜甜，徐敬东，张建忠.基于模糊综合评判的多sink最优路由算法［J］.计算机工程，2012，38（7）：73-76.

［7］任小洪，乐英高，徐卫东.无线传感ZigBee技术在物联网中的应用［J］.电子技术应用，2011，37（6）：81-83.

［8］韩凯州，马福昌.无线传感器网络中多Sink节点位置部署研究［J］.传感器与微系统，2014，33（3）：37-39.

［9］潘耘，李嫣，李晋凯.无线传感器网络中的多Sink节点的放置问题［J］.计算机研究与发展，2010，47（2）：92-95.

［10］刘长平，叶春明.一种新颖的仿生群智能优化算法：萤火虫算法［J］.计算机应用研究，2011，28（9）：3295-3297.

［11］徐久强，柏大治，罗玎玎.遗传算法在WSNs多Sink节点布局中的应用［J］.东北大学学报（自然科学版），2008，29（6）：815-818.

［12］陈志雄，潘耘，李嫣.用改进蚁群算法求解无线传感器网络多sink节点关联问题［J］.计算机应用与软件，2012，29（2）：246-249.

（编辑 赵蓉）

Research on Multi-Sink Node Association Algorithm of Internet of Things Perception Layer

WANG Hua-dong，WANG Da-yu
（School of Computer Science and Technology，Zhoukou Normal University，Zhoukou Henan 466001，China）

In large-scale wireless sensor net works monitoring environment，using a single Sink node in the network is likely to cause"energy hole"effect，while Sink node number and location of proper deployment can cost effectively extend the lifetime of wireless sensor networks，control network costs，at the same time multi-Sink node number and location is an NP-hard problem.Therefore propose the firefly algorithm to solve the problems of the multiple Sink node layout model calculation，and analyses the calculation accuracy and efficiency of algorithm.Theoretical analysis and simulation results show that the proposed in this paper based on the firefly algorithm Sink node layout model with random distribution，based on genetic algorithm，ant colony algorithm Sink node deployment algorithm，can effectively reduce the energy consumption of wireless sensor networks，reducing end-to-end network delay，reduce network deployment costs，improve network efficiency and prolong the lifetime of the network.

internet of things；perception layer；multi-sink node

TH166；TG506

A

1001-2265（2015）10-0023-05 DOI：10.13462/j.cnki.mmtamt.2015.10.007

2014-12-15；

2015-01-13

国家自然科学基金（61103143）；河南省基础与前沿技术研究项目（142300410339，132300410479）

王华东（1977—），男，河南沈丘人，周口师范学院副教授，硕士，研究方向为计算机网络与通信，无线传感器网络，（E-mail）zhoukou985211@163.com。