基于惯性导航+通信信号测角信息融合的车辆行进间高精度定位方法

高军军 龙杰 刘琰 余跃 黄四牛

在实战环境下,快速获得车辆的高精度定位信息,对于提高其整体作战性能十分重要.车辆上一般配备有多种导航系统,主要包括卫星导航和惯性导航系统,可以获得车辆的位置信息[1].

然而,在复杂电子对抗环境下卫星导航链路很脆弱,容易受到外部干扰和欺骗,或者在山区等特殊地理环境下,阻挡易造成导航卫星不可见[1−2].在卫星导航系统不可用的降级条件下,车载惯性导航系统若长时间得不到精确信息进行修正,则其输出的位置将包含较大的时间积累误差,以至不能满足实际需求.

针对上述问题,本文利用可与车辆进行双向短距离通信的路边单元进行辅助,提出了一种基于车载惯性导航+通信信号测角信息融合的车辆行进间高精度定位方法.车辆接收路边单元发送的定位辅助信息,并对路边单元发射的通信信号的角度特征量进行测量,并利用相对几何关系,解析得到车辆精确位置.定位场景如图1所示.

图1 车辆定位场景示意图

1 系统功能与组成

1.1 车辆组成

车辆应具备与路边单元进行双向短距离通信的功能,并通过控制帧请求路边单元发送定位辅助信息.同时,车辆应能够对路边单元发射的通信信号的到达角度进行测量.

车辆组成如图2所示,主要包括惯性导航系统、信息处理与控制单元、通信基带信号处理单元、干涉测角单元、发射射频通道、接收射频通道、发射天线和接收天线.

1.2 路边单元组成

路边单元应能够在野外环境下长时间、低功耗地自主待机工作,并支持被车辆唤醒.同时,可作为数据存储和中继节点,使车辆通过路边单元与其他节点进行信息交互.

路边单元用于辅助车辆进行定位,其组成如图3所示,主要包括内置天线、唤醒模块、发射射频通道、接收射频通道、信号处理单元、数据存储单元、电源模块和外部接口单元.

2 定位原理

车辆通过发射无线电信号唤醒路边单元开始工作.在图1中,当车辆行驶到A1点时,车载干涉测角单元估计得到路边单元发射的无线电信号的到达角度θ1;当发射车行驶到A2点时,同理测量得到无线电信号的到达角度θ2.

同时,车载的信息处理与控制单元基于惯性导航信息计算得到两次测角点之间的直线距离S.

在得到两次测角点的角度信息θ1和θ2、车辆行驶直线距离S基础上.利用图1中所示的几何关系,可得到车辆在A2点时与路边单元之间的距离值计算公式如下

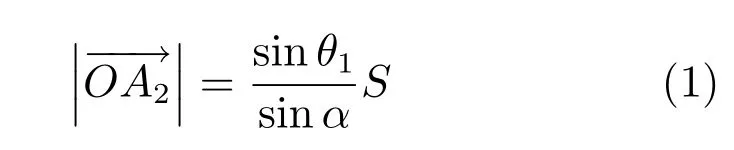
其中α=θ2−θ1,为从路边单元观测到的两次测角点的张角.

由于路边单元的埋设位置已经预先精确标定,因此,车载的通信基带信号处理单元可对路边单元发送的定位辅助进行解析,从而得到路边单元的坐标等信息.上面已经求解得到了车辆与路边单元之间的距离,依据车载系统提供的角度信息,进行相应的坐标转换、投影,即可得到车辆在A2点的精确坐标.坐标转换和投影在本文不赘述,关键是获取车辆与路边单元之间的精确距离值.

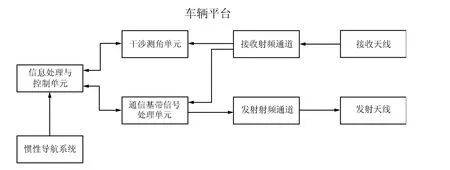
图2 车辆组成示意图

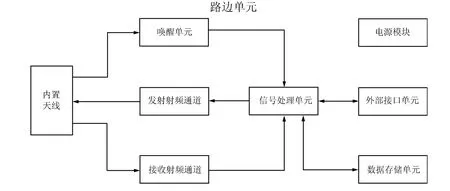
图3 路边单元组成示意图

3 干涉测角原理

本文采用相位干涉测角方法,根据路边单元发射的通信信号,提取车载接收天线单元之间的信号相位差,从而获得目标信号的到达角度.

基于相位干涉的测角计算公式为[3−4]

其中λ为信号波长,d为车载测角天线的基线长度,∆φ为不同车载天线接收信号之间的相位差.

干涉测向精度公式可近似表达为[3]

其中为σθ测量角度的标准差,σ∆φ为相位差测量的标准差,其与信噪比有关.

测角精度与基线长度、信噪比的关系如图4所示.为了提高测角精度,应该在保证无模糊的条件下,尽量增加基线长度,并通过链路预算保证足够高的信噪比.

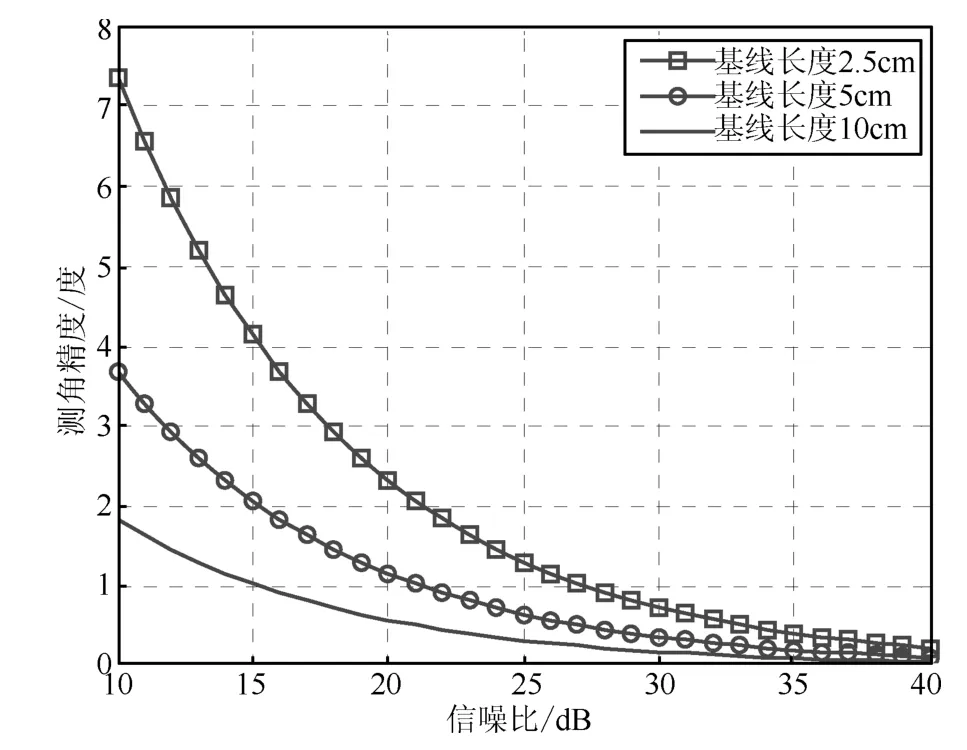
图4 干涉测角精度与基线长度、信噪比的关系

4 误差分析

4.1 定位误差影响因素

根据上一小节中定位原理分析,可知车辆定位误差主要受以下因素影响:

1)路边单元的位置标定误差;

2)两次测角点之间的直线距离测量误差;

3)车载干涉测角单元的角度测量误差.

路边单元的位置是固定的,因此,其位置参数的标定可采用多次标定取平均值的方法,减小随机误差的影响,一般其标定精度较高,其误差对车辆定位精度的影响在此忽略不计.

两次测角点之间的直线距离通过惯性导航系统在两个时刻给出的位置值相减得到,因此,惯导系统的误差特性决定了该距离的测量误差.惯导在长时间未修正的情况下,由于误差积累,其输出的位置绝对值的误差比较大.但在本文解决的问题中,两次测角点之间的时间间隔一般较小,以车速为72km/h,距离20m为例,时间间隔为1s.在短时间间隔内,惯导的误差特性基本不变且积累误差很小,通过两次位置值相减,即可消除掉第一次测角点之前积累的误差量,从而得到比较精确的相对距离测量值.因此,在以下的分析中,不考虑两次测角点间距离测量误差.

以下主要分析测角非理想性对定位精度的影响.假设车载干涉测角单元对来波角度的最大估计误差为∆θe,max,则考虑最坏情况时,车辆与路边单元之间的距离计算公式为

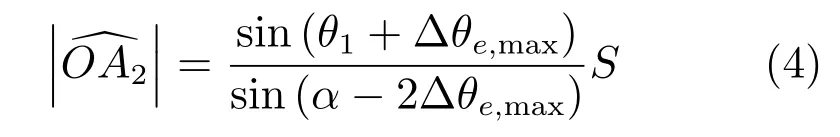
下面分析存在测角误差情况下,测角点之间距离、初次测角点的选择,对定位精度的影响.

4.2 两次测角点之间距离对定位精度影响

在车辆行驶路线与路边单元之间垂直距离给定的情况下,若两次测角点距离越小,则张角α越小,此时测角误差对定位精度的影响则越大.假设两次测角点对称分布于路边单元两侧,在不同的最大测角误差值情况下,定位精度随着两次测角点之间距离S的变化如图5所示.

图5 定位误差随两次测角点距离变化曲线

图5的结果表明,在最大测角误差值确定的条件下,应尽量使两次测角点之间距离增加,从而减小测角误差对定位精度的影响,具体取值应根据定位误差要求等参数确定.

4.3 初始测角点对定位精度影响

除了两次测角点之间距离,初始测角点的选择也会造成测角误差对定位精度的不同影响.在相同测角点距离的情况下,若初始测角点角度值θ1越小,即车辆离路边单元越远,则张角α的值也会越小,使得测角误差对定位精度影响增加.

假设两次测角点之间距离取定值,在不同的最大测角误差情况下,定位精度随着初始测角点角度值的变化如图6所示.仿真结果表明,初始测角点角度值应选取在范围内(50◦,70◦),使得张角α最大化,减小测角误差对定位精度的影响.

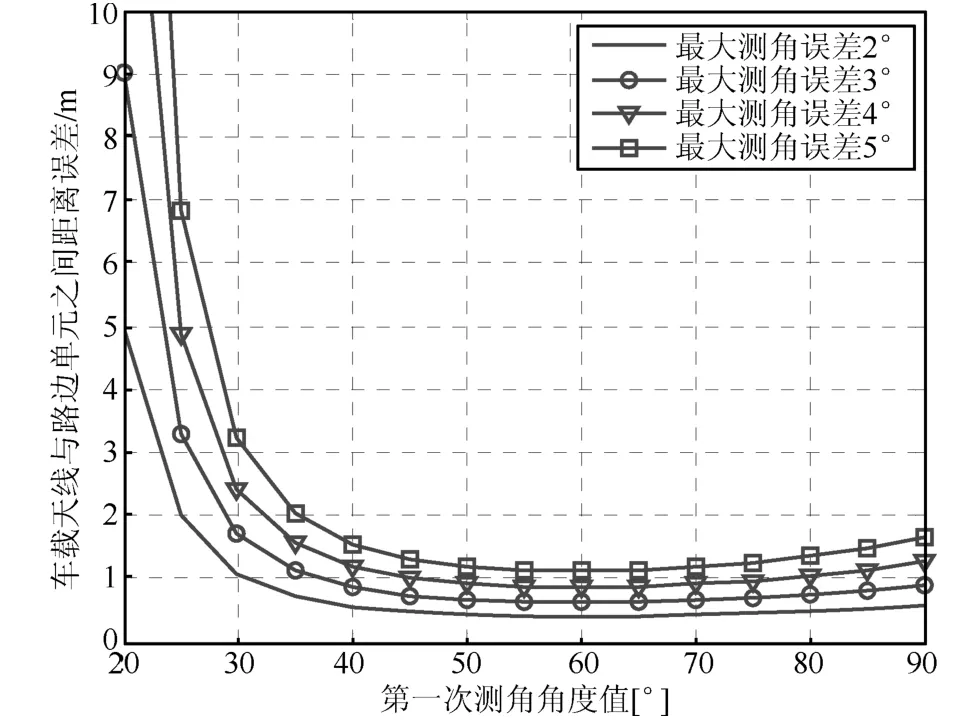
图6 定位误差随初始测角点角度值的变化曲线

4.4 减小定位误差的措施

综合上述分析,通过减小测角误差,以及合理的测角点之间距离参数选择等,可以有效减小各种因素对定位精度的影响.可采取以下有效措施减小定位误差:

1)增加车载天线高度,减小地面发射多径信号对车载干涉测角单元测角精度的影响;

2)依据通信距离等参数,进行合理的链路预算,保证车载接收天线端接收信号的信噪比,提高测角精度;

3)在实际情况允许的条件下,在测角不同阶段可合理规划选择不同长度的干涉测角基线,提高测角精度;

4)增加两次测角点之间的距离,减小测角误差对定位精度的影响;

5)合理选择初次测角点位置,增加两次测角点之间张角,减小测角误差对定位精度的影响.

5 结论

在卫星导航不可用的降级环境下,若车载惯性导航系统一定时间内得不到精确修正,其输出的车辆位置值的误差将较大.为了解决上述问题,本文提出了一种在路边单元辅助下,基于惯性导航+通信信号测角信息融合的车辆行进间高精度定位方法,并对其定位原理和误差影响因素进行了详细分析,最后给出了减小定位误差的有效措施.仿真结果表明,通过合理的参数选择,车辆定位精度可达到米级,解决了降级环境下车辆行进间高精度定位问题.