基于攻击面度量的动态目标防御效能评估方法

杨林 张义荣 杨峰 马琳茹 李京鹏

攻击面是攻击者进入信息系统并可能造成破坏的一系列途径,即攻击时使用的操作系统、软件、数据和网络等资源.攻击面越大,系统越不安全;系统的安全漏洞很难彻底根除,在漏洞必然存在的情况下,降低安全风险的有效办法是缩小系统攻击面.动态目标防御的主要思想是向攻击者呈现不断变化的攻击面,增加攻击者探测和利用攻击面的难度,以达到减小系统攻击面的效果.概而言之,安全防护体系不断完善的过程,就是促使攻击面不断缩小的过程[1].

通过动态变化实现安全的想法主要基于自动生成能改变系统某些特性的系统变量或目标程序.动态目标防御作为一种可能“改变游戏规则”的潜在方法,正受到业界广泛关注.按照动态使用系统资源不同,动态目标防御技术主要有网络配置随机化、指令集随机化、软件多态化等[2−4].Shaer.E.Al[5]等提出了一种称为“变形网络”(MUTE)的动态目标防御架构,能够随机动态地改变网络配置(如IP地址、路由)等,以抵御网络扫描、拒绝服务、僵尸网络等攻击行为.Kc.G.S[6]等研究了基于硬件的低开销指令集随机化方法,并利用Bochs X86仿真器评估了该方法在解释型语言(如Perl、SQL等)中的适用性.Shacham.H[7]等研究了进程地址空间布局随机化(ALSR)问题,表明32位系统缺乏足够的熵导致ALSR不是十分有效.Jacob.M[8]等对程序编译器进行修改,通过添加指令产生不返回的代码,能够阻止部分代码重用攻击.Yiu.H[9]等通过配置具有不同软件堆栈的虚拟服务器集群生成持续变化、不可预知的Web服务架构,来挫败SQL注入、跨站脚本等Web攻击.

上述工作重点关注动态目标防御的具体实现技术,缺乏对系统变化攻击面的形式化分析和度量方法,难以评估动态目标防御的综合效能.本文提出了一种基于马尔可夫(Markov)链的攻击面建模度量方法,探索通过攻击探测概率指标对变化攻击面进行定量度量,并对攻防博弈中动态目标防御方法的有效性和实施策略进行分析验证.

1 模型描述

控制、监测和动态等3类安全防护手段可作用于攻击面W,假设系统的每个输入点都可能成为一个攻击点,这些攻击点汇集成攻击面,因此W可以看作系统所有输入点的数量.

1)控制手段:一种直接减少攻击面状态空间的方法,采用控制后攻击面变化为Wc=W−PC,其中C为控制措施.

2)监测手段:一种间接减小攻击面状态空间的方法,通过监测攻击可为控制提供辅助支持.采用监测后攻击面变化为Wm=Wc−PM,其中M为监测措施.

3)动态手段:攻击面在各个状态间以某种概率进行状态迁移.在各个状态间迁移的概率构成一个转移概率矩阵,由于某时刻之后的状态只与该时刻的状态有关,而与之前的状态无关.这种数学模型符合时间离散、状态离散的Markov过程条件[10],即Markov链.

不管初始状态如何,系统经过有限步迁移后最终会达到平衡.因此,系统攻击面最终落在某个状态的概率是可以确定的,可计算攻击面的数学期望值,即动态变化期望达到的防御效果,如图1所示.

图1 攻击面状态迁移示意图

定义1.假设系统状态S为离散集合A={A0,A1,···,An},状态Ai的攻击点数量为Ki,状态间迁移概率为Pti,攻击面探测概率Pdi.那么,系统状态转移矩阵是一个(n+1)阶方阵,可定义为:

1.1 变化攻击面度量方法

根据攻击者和防御者对状态攻击面的掌握程度,可以将模型分为以下4种情况:

Case 1.防御者不清楚状态攻击面具体情况,系统攻击点的迁移是随机的,攻击者具有足够的能力在时间间隔(∆t)内去掌握每个时刻的攻击路径,即Pdi=1.

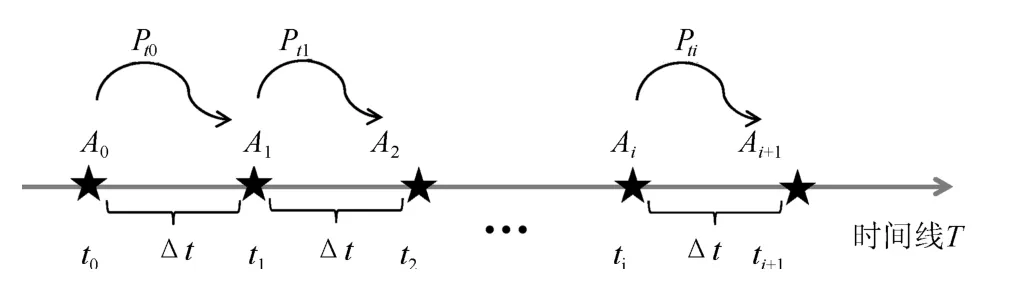
图2 攻击面Markov链状态迁移1

Case 2.防御者清楚状态攻击面具体情况,防御者有意引导系统向攻击面减小的方向迁移,即∀i,ki≤k0.同时,攻击者具有足够的能力在时间间隔(∆t)内去掌握每个时刻的攻击路径.此种情况与Case 1类似,仅相当于状态空间有所缩减.

Case 3.防御者不清楚状态攻击面具体情况,系统攻击点的迁移是随机的,而攻击者可能没有足够的能力在时间间隔(∆t)内去掌握每个时刻的攻击路径.假设每种状态的攻击面探测概率为Pd,Pd∈[0,1],此种情况与Case 1类似,相当于在状态空间集合{AiPdi}中求解Markov链平稳方程.如果当∀i,Pdi=1,此时退化为Case 1.

图3 攻击面Markov链状态迁移2

Case 4.防御者清楚状态攻击面具体情况,而攻击者可能没有足够的能力在时间间隔(∆t)内去掌握每个时刻的攻击路径,此种情况对防御者最为有利.假设每种状态的攻击面探测概率为Pd,Pd∈[0,1],此种情况与Case 2类似,相当于在状态空间集合{AiPdi}中求解Markov链平稳方程.当∀i,Pdi=1,此时退化为Case 2.

若系统状态迁移概率矩阵为Pt,那么根据方程

可以求出Markov链的平稳分布X∗.

如果攻击面探测概率向量为Pd,则系统状态的期望为

站在防御者角度,希望采用合适的动态手段和系统状态迁移策略,使得

其中k0为静态系统攻击面初始值,即使得系统攻击面往缩小的趋势发展.

1.2 攻击探测概率度量方法

攻击探测概率Pd是影响动态系统攻击面的重要指标,对攻击面的数学期望影响甚大,可从状态迁移速率、随机化程度和状态空间大小等维度进行量化.

定义2.假设动态系统S的状态迁移时间间隔∆t∈[0,T0],随机化程度为R∈[0,1],状态空间大小为状态数N∈[0,N0],探测防护能力为探测报文拦截率L∈[0,1],则动态系统S的攻击探测速率Pd为

其中,T0定义为探测到所有攻击面所需最大时间,N0定义为防御者可变换的最大状态空间数.

2 算例分析

假设某云中心初始状态的攻击面可在5个状态间迁移,攻击面S的状态空间为A={A0,A1,A2,A3,A4}.假设该状态的转移规则是:如果在迁移前,它在A1,A2,A3这几个状态上,那么就分别以1/3的概率向前或向后迁移一个状态,或者停留在原处;如果迁移前,它在A0这点上,那么就以概率1迁移到A1这一点;如果在移动前,它在A4这点上,那么就以概率1转移到A3这一点,因此系统转移概率矩阵为:

平稳状态向量X=(x1,x2,x3,x4,x5)由X=X∗P计算得出:

上述方程解得

经过有限步状态转移后,系统状态的期望为:

2.1 变化攻击面结果分析

Case 1.防御者不清楚状态攻击面具体情况,系统攻击点的迁移是随机的,攻击者具有足够的能力在时间间隔内掌握每个时刻的攻击路径.

假设初始状态攻击面k0=4,k1=7,k2=3,k3=2,k4=5,那么攻击面的期望A∗=4.09.

Case 2.防御者清楚状态攻击面具体情况,引导系统向攻击面减小的方向迁移,攻击者具有足够的能力在时间间隔内掌握每个时刻的攻击路径.

假设初始状态攻击面k0=4,k1=3,k2=2,k3=4,k4=1,那么攻击面数学期望A∗=2.90.

以科学理论为名称，如试用版(上海)高中地理新教材第一册的“宇宙大爆炸”，第二册的“中心地理论”等专栏，虽然只是介绍科学理论的主要内容及形成过程，但从中能反映伽莫夫、魏格纳、勒皮雄、克里斯泰勒等科学家为创立这些新的科学理论所付出的艰辛努力和勇于探索的精神。

Case 3.防御者不清楚状态攻击面具体情况,系统攻击点的迁移是随机的,攻击者可能没有足够的能力在时间间隔内掌握每个时刻的攻击路径.

与Case 1类似,假设初始状态攻击面k0=4,k1=7,k2=9,k3=2,k4=5,攻击面探测概率Pd0=0.3,Pd1=0.5,Pd2=0.4,Pd3=0.2,Pd4=0.6,那么攻击面的数学期望A∗=2.43.

Case 4.防御者清楚状态攻击面具体情况,有意引导系统向攻击面减小的方向迁移,攻击者可能没有足够的能力在时间间隔内掌握每个时刻的攻击路径.

与Case 2类似,假设初始状态攻击面k0=4,k1=3,k2=2,k3=4,k4=1,攻击面探测概率Pd0=0.3,Pd1=0.5,Pd2=0.4,Pd3=0.2,Pd4=0.6,那么攻击面的数学期望A∗=1.009

站在防御者角度,希望采用合适的防护手段和系统状态迁移策略,使得

为简化起见,假设每次攻击探测概率Pdi为相同常量,则

此即为系统状态调整策略是否有效的拐点,如图4所示.

图4 系统动态调整拐点

可见,当0.698时,动态系统攻击面的数学期望值大于静态系统的攻击面值,此时进行动态变化调整并无效果.

2.2 攻击探测概率简化分析

攻击探测概率与多种因素相关,如攻击者技能水平、对系统掌握程度、计算资源多寡、分析时间长短等.为简化起见,假设在给定计算资源、不考虑随机化程度、状态空间等情况下,探测概率仅与允许攻击者分析系统的时间呈线性关系,且系统状态进行周期变化,则式(5)变为:

其中,∆t为状态发生变化的时间间隔,T0为攻击者研究出当前时刻系统所有攻击点需要的时间周期.

假定在攻击资源一定的情况下,某攻击组织可在12h内分析系统当前状态的所有攻击点.在上述算例Case 3下,可由公式

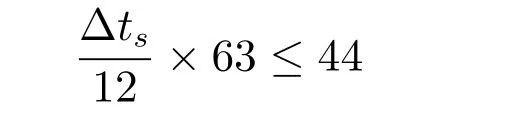
由此可见,动态防御技术未必一定能减小系统攻击面,其实际效能与攻击者、防御者对状态攻击面的掌握程度密切相关.例如,在防御者不清楚状态攻击面具体情况下,动态系统攻击面甚至可能比静态系统攻击面更大.而攻击探测概率则是影响动态系统攻击面的重要指标,攻击活动被防御者及时探测的概率越低,动态系统攻击面越小.

3 结论

本文基于马尔可夫链理论对信息系统动态防御效能进行了模型构建和实例分析,并验证了相关模型的有效性和合理性.研究结论表明为取得动态防御效果,动态防御技术必须满足以下条件:1)快速而不可预测的状态迁移,即状态动态迁移必须快速以保证攻击者没有足够的时间和空间去侦察、探测目标;2)足够多的状态空间,以减少不同状态间攻击面的重复度,增加攻击者对系统掌握的难度;3)透明的状态迁移,即在系统状态迁移过程中被保护目标必须是“透明”的,以保证整个会话和服务不会因状态迁移而中断.

目前的工作仅是对攻击面建模进行了一些初步探索.为了更精确刻画变化攻击面度量模型,仍有大量研究有待开展,相关工作包括模型可扩展性、攻击者建模、动态迁移策略最优化等.在模型可扩展性方面,可进一步考虑攻击面与系统安全漏洞的关系,系统动态变化时安全漏洞的性质和数量变化可能导致攻击面发生突变,目前对系统漏洞的形式化描述仍是难题;在攻击者建模方面,由于攻击类型和方法的复杂性(如旁路攻击、隐蔽通道等)使得攻击建模十分困难[11],已有的攻击图、攻击树等模型缺乏定量描述能力,可尝试进一步根据攻击者类型(个人/组织/国家)、空间资源(单点/协同)、时间资源(分/小时/天)等精细分析;在动态迁移策略最优化方面,寻找最优的动态迁移策略是项技术挑战,系统的动态变化应该快速和不可预测,并对外部攻击具有感知能力,但这种动态变化要求在网络基础设施、协议或终端软件方面具有灵活可伸缩性和可部署性,实践上存在困难,博弈论[12]的引入可能是解决问题的一种方法,可进一步深入研究.