湿法脱硫吸收塔出口直插式氧量探头滤网的温度场模拟

曾想

（广东大唐国际潮州发电有限责任公司，广东潮州 521000）

湿法脱硫吸收塔出口直插式氧量探头滤网的温度场模拟

曾想

（广东大唐国际潮州发电有限责任公司，广东潮州 521000）

随着全球工业制造格局的变化，造就了我国经济快速发展。因此使我国能源消耗急剧增加。本文章针对湿法脱硫吸收塔出口氧量探头滤网堵塞问题。通过参照实际烟气参数与氧量探头运行时的相关参数，运用成熟的理论模型进行数值模拟；并且分析数值模拟的结果得出氧量探头在相应的烟气温度区间内滤网长度的对应值。为解决滤网堵塞问题提供数值依据。

湿法脱硫 直插式氧量探头 温度场

1　研究背景

随着经济的快速发展全国总装机容量不断上涨。伴随着工业的高速发展与技术的相对落后，电力行业中的燃煤机组仍然是发电企业中的主流。与此同时，伴随着我国工业实力的发展，作为代价自然环境也遭到了严重的破坏。随着政策的调整与各个行业的努力，火电厂作为重大污染源SO2的源头，分分在烟气排放前加装了脱硫装置。湿法脱硫作为脱硫效率最高的装置也成为了各个火电厂的首选。

本文利用模拟计算的方式，对以氧量探头为代表的脱硫装置出口直插式探头滤网套管金属壁进行温度场的模拟。由于氧量探头内部包含有加热丝（保障锆电池正常运行），因此利用加热丝的余热来加热滤网则是一种不过的选择。文章中用45℃到55℃作为环境参考温度，选择固定的金属导热参数与流体参数，已加热丝至滤网的距离作为变量，采用经典的温度场计算方式进行计算。得到诸多具有参考价值的模拟结果。

2　数学建模

文中氧量探头的模型是基于直插式氧量探头。该种氧量探头测量是通过高温（750℃-840℃）下氧化锆在氧浓度存在差值的情况下产生电势差，通过测量电势差来显示氧量。在特定的安装位置，入脱硫吸收塔出口。由于烟气温度的降低，使得氧量探头前端滤网温度降至露点以下，以至滤网处烟气中水分凝结堵塞滤网。但与此同时由于氧量探头中存在加热丝，使得氧量探头的滤网能通过金属套管获得加热丝的余热提高自身温度蒸发水分。

本文利用上述矛盾通过数值计算的方式找出平衡的区间，为企业氧量探头选型提供理论依据。

图1　氧量探头简化释义图

如图1所示氧量探头管壁厚度为0.005m，滤网固定在滤网套管上，套管长度为L1、套管外壁直径为0.056m、套管内壁直径为0.046m。图1中L2表示加热丝至滤网的距离。若L1＞L2时加热丝在滤网套管内部，在这种情况下加热丝的热量通过套管壁直接传导至滤网。若L1＜L2时热量传导至滤网的过程中，由于螺纹接口的存在使得部分热量在其中耗散。本文在以上所述的两种情况下都进行了数值模拟。

在数值模拟计算中采用的参数：

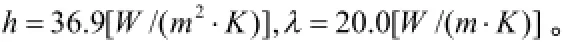
h为流体参数，λ为管壁材料（设为306不锈钢）传热系数。

3　数学模型

在探头中的大量原件为中轴线对称，因此在数学模型建立时，采用圆柱坐标系（cylindrical coordinates）建立稳态温度场其中t表示温度；R表示延探头套管切向位移；Z表示延探头套管长度方向位移；θ表示角度（由于探头的对称性，在计算时令

因加热丝为圆柱形长度非0，当选择对应向外导热切面ZΔ足够小时。可以认为在该切面任意径向可以表示为：

在本文中采用在圆柱坐标系下的拉布拉斯方程作为控制方程，由于我们在计算时忽略烟道烟气流场对氧量探头导热套内温度场的影响。因此在传热套管中相同R与Z的圆上t为固定值（即控制方程可以表示为：

我们模拟的是将探头放置在空气或烟气等流体中，因此探头外表面符合牛顿冷却定律，即选择传热学中的第三类边界条件。即：其中w表示换热表面的外法线。

4　模拟结果

在初始条件的模拟中，由于在加热丝与金属管壁之间存在着多种传热方式（热辐射、热交换等）。我们通过现场实际测量，运用传热原理反推出金属管内壁稳态温度为205.8℃。在烟道中烟气温度大多出于45℃-55℃之间，因此进行数值模拟时环境温度ft取值在45℃-55℃之间。

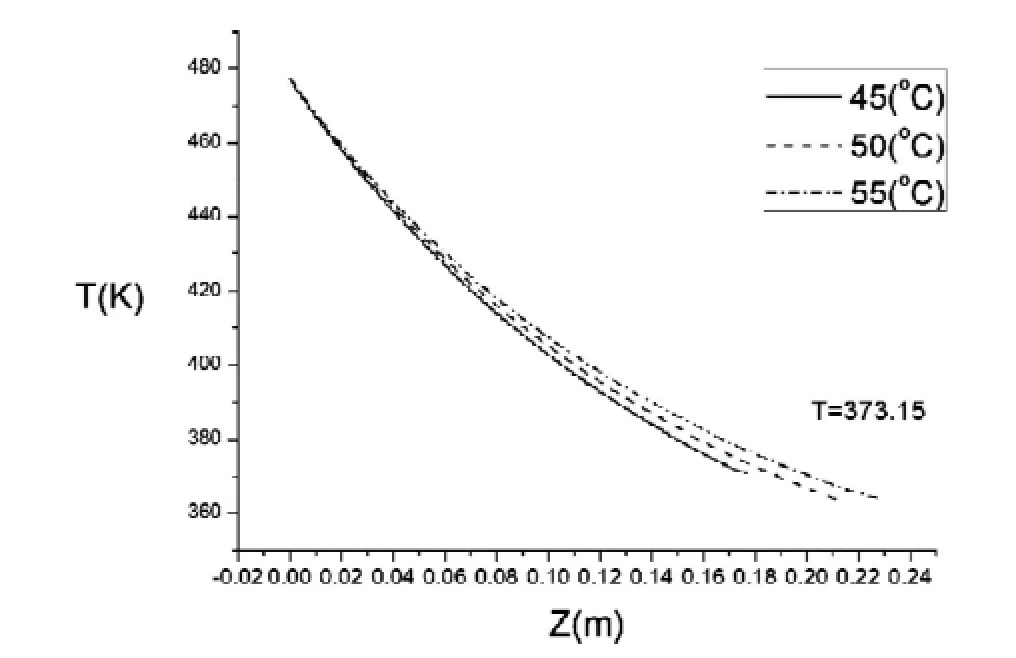
图2　为环境温度tf分别在45、50、55℃的情况下温度在套管外壁分布的曲线

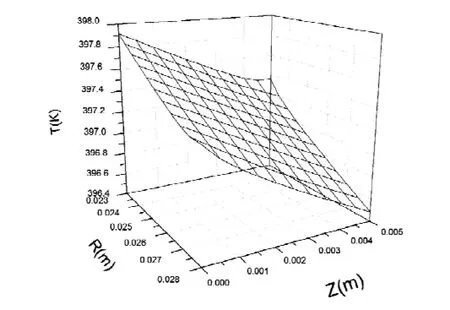
图3　.A

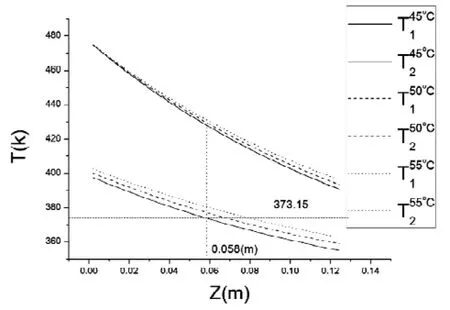
图3　.B

图3　.C

4.1加热丝（热源）在滤网套管内（L1＞L2）

当L1＞L2时，计算中Z=L2。在图2中我们可以清楚的看出以下两点：其一，随着环境温度的提高在同样的初始条件下，管壁温度降至373.15K（100℃）的距离越长；其二，管壁温度随传导距离的变化并非线性关系，由于单位长度的管壁随表面温度的下降，耗散在流体中的热量减少，当传导距离足够长时温度降趋于环境温度。

在工程实践中，热源到滤网的距离小于套管螺纹到滤网（热源与滤网通过金属管壁直接连接）。热量能以最有效的方式传导至滤网，以保持滤网的相对高温进而保证其干燥。

4.2加热丝（热源）在滤网套管外（L1＜L2）

当L1＜L2时，即导热过程中还需要考虑经过螺纹时热量的损失，计算中Z=L2-L1。计算在不同材质之间仅考虑一种传热方式（牛顿冷却公式）。下文中我们做了以下两种方式的计算。第一种边界情况，假设螺纹接触面压缩到一个平面，即（Z=Z0）平面。在此情况下温度场模拟的4个边界条件中仅一边为螺纹接触平面，其余3边为环境温度。第二种边界情况：在螺纹接触面延长，在第一种情况下将R=0. 023边界条件设螺纹接触面。即4个边界条件中有2条边为螺纹接触面。

图3.A：第二种边界情况下，当环境温度Tf=45℃时螺纹后管壁在Z-R平面温度场分布。图3.B：第二种边界情况下，环境温度分别为45℃、50℃、55℃，当螺纹到热源在管壁距离为Z时，螺纹前的温度为T1螺纹后的温度为T2。C：当环境温度为50℃时，dTk1为第一种边界情况下的温降；dTk2为第二种边界情况下的温降。从图3.B中通

过辅助线373，15（100℃）可以看出，在此种情况下当螺纹至加热丝的距离小于0.058m时，T2的温度大于100℃。通过图3.C可以明显看出：对比两种情况下的温度降曲线不难发现在两种不同边界情况下，温降的曲线也不同。在第二种边界情况下，温降明显小于第一种情况。这是由于接触面的增加使传热量得到提升。由此我们可以得知在实际工程应用中增加接口处两段套管之间的接触面能有效的减少热量在传导时的损失，从而提高滤网套管前段温度。

5　结语

本文通过数值计算的方式得到氧量探头滤网套管在45-55℃的环境温度下的稳态温度场以及温度曲线。这种稳态主要是热能恒定供给（固定初始条件）与金属表面耗散热量（牛顿冷却公式边界条件）的平衡。我们描绘滤网套管外壁温度与其到热源距离的曲线，通过曲线与100℃直线交叉点的位置来判断滤网套管长度的极限值。

工程应用中氧量探头滤网套管有两种形制，在文中使用一、二两种边界条件表示出来，即L1＞L2与L1＜L2时。在两种情况下的最大差被在于热能在沿滤网套管管壁传导过程中是有否有通过螺纹节时的能聊耗散。在第一种情况中（L1＞L2）由于没有螺纹节的能量耗散，热能能够充分传导至滤网前段，因此在这一滤网套管的形制下滤网与加热丝的极限距离较长可在18-20cm左右；在第二种情况中（L1＜L2）由于螺纹节的存在，使得热量在传导过程中有额外的耗散，因此在这一滤网套管的形制下滤网与加热丝的极限距离较短在5-6cm左右。这里需要提醒的是，螺纹与滤网的距离尽可能的小。

本文在数值计算过程中采用，氧量探头滤网套管的金属传热参数以及烟气流动参数为固定值，但由于烟气温度及流速值在一定范围内文本的模拟结果具有一定的代表性。在实际应用中由于环境压力并非标准大气压露点温度会有所变化，但该计算仍然具有参考价值。通过实践中的观察，其结果与模拟结果相符。