准幻方矩阵的几个性质

刘 玉

（韩山师范学院 数学与统计学院，广东 潮州 521041）

幻方矩阵已有很多研究和应用[1-4]，文献[5]和[6]给出了准幻方矩阵的定义并讨论了这类矩阵的若干性质，得出了一些很好的结论，本文在此基础上研究了准幻方矩阵的几个性质，得出了一些新的结果.

1 预备知识

本文用AT表示n 阶矩阵A 的转置矩阵；用I 表示单位矩阵；用e 表示所有元素都是1 的列向量，即e=(1 ，1，…,1)T；用J 表示n 阶全1矩阵，即所有的元素都是1的n 阶矩阵；用Rn×n表示实数域上n阶矩阵的全体；如无特别说明，本文所讨论的矩阵A均指n 阶实矩阵；一个n 阶矩阵P 若它的每一行和每一列有且仅有一个非零元素1而其余各元素全为0，则称矩阵P 为n 阶置换矩阵，可以看出若设为n 阶置换矩阵的全体，则共有n!个不同的置换矩阵.

定义1[7]设A ∈Rn×n，P为n 阶置换矩阵，若其中A11为r×r子矩阵，A22为(n-r)×(n-r)子矩阵，则称矩阵A是可约矩阵.

定义2[1]设A=(aij)∈Rn×n，如果

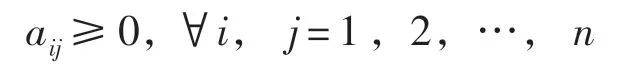
即A 的所有元素是非负的，则称A 为非负矩阵，记作A ≥0.

定义3[5]设A ∈Rn×n，如果满足Ae=ATe=ae（其中a ∈R），则A 称为准幻方矩阵.

由A 与a的关系可记为a=ρ(A).特别的ρ(A)=0当时则A 称为双心矩阵，若A ≥0且ρ(A)=1则A 称为双随机矩阵.

定义4[7]设A,B ∈Rn×n，P 为n 阶置换矩阵，若PAPT=B，则称矩阵A 置换相似于矩阵B.

引理[3]1 （Birkhoff 定理）设A 是n 阶双随机矩阵，则A 可表为n 阶置换矩阵全体的凸线性组合.即

引理[3]2 设A为任意n阶准幻方矩阵，设m为A中最小的元素，则A-mJ为非负准幻方矩阵.

引理3 设A ∈Rn×n，若A 是非负的准幻方矩阵，则A 可表示为n 阶置换矩阵的凸线性组合.即

证明 设A ∈Rn×n，且A 是非负的准幻方矩阵，

若ρ()A =0，易知A=0，此时ai=0，结论成立；

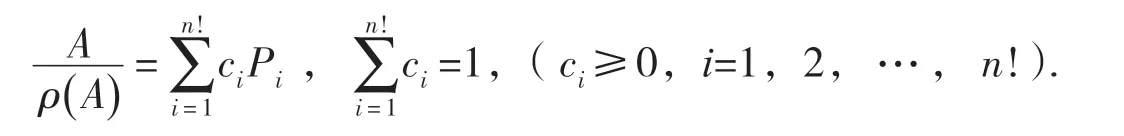
故

设ρ(A) ci=ai（ci≥0，i=1，2，…，n!），可见ai∈R （i=1，2，…，n!）

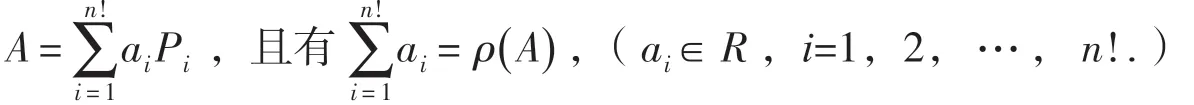
引理5[8]设A ∈Rn×n，若A 是双随机矩阵，则存在n 阶置换矩阵P，使得PAPT=A1⊕A2⊕…⊕Ap，其中Ai为ni阶双随机矩阵(i=1,2,…p,n1+n2+…+np=n).即，双随机矩阵置换相似于双随机矩阵的直和.

2 准幻方矩阵的性质

定理1 设A ∈Rn×n，若A 是准幻方矩阵同时又是反对称矩阵，则A 为双心矩阵

证明 设A ∈Rn×n，若A 是反对称矩阵，则A=-AT，故Ae=-ATe，又因A 是准幻方矩阵，则Ae=ATe=ρ(A)e，从而得到ρ(A) e=-ρ(A) e，故ρ(A) =0，即A 为双心矩阵.

定理2 设A ∈Rn×n，若A 是双随机矩阵同时又是正交矩阵，则A 为置换矩阵.

证明 设A ∈Rn×n，若A 是双随机矩阵，则0 ≤aij≤1，j=1，2，…，n；又因A 为正交矩阵则又当存在aij满足0＜aij＜1 时，有此时与A 是正交矩阵矛盾.故只有aij=0或aij=1.又推出A 的每一行有且仅有一个元素为1，其余各元素全为0.

同理可推出A 的每一列有且仅有一个元素为1，其余各元素全为0.

综上可知A 为置换矩阵.

定理3 设A ∈Rn×n，若A 是准幻方矩阵且ρ(A)≠0，若A 有且仅有n个非零元素，则A=ρ(A)P（P为n 阶置换矩阵）.

证明 由若A 是准幻方矩阵且ρ(A)≠0，可知A的每一行及每一列至少有1个非零元素，否则与ρ(A)≠0矛盾.

由A 有且仅有n个非零元素，可知A 的每一行及每一列至多只有1个非零元素，否则与这个条件矛盾.

综上可知A 的每一行及每一列有且仅有一个非零元素，又为A 准幻方矩阵，故A 中的非零元素都为ρ(A) ，即有A=ρ(A) P，其中P为n 阶置换矩阵.

定理4 设A ∈Rn×n，若A 是准幻方矩阵，则A 可表示为n 阶置换矩阵的线性组合.即

证明 设A ∈Rn×n，若A 是准幻方矩阵，设m为A中最小的元素，由引理2知A-m J为非负准幻方矩阵，由引理3证明可知

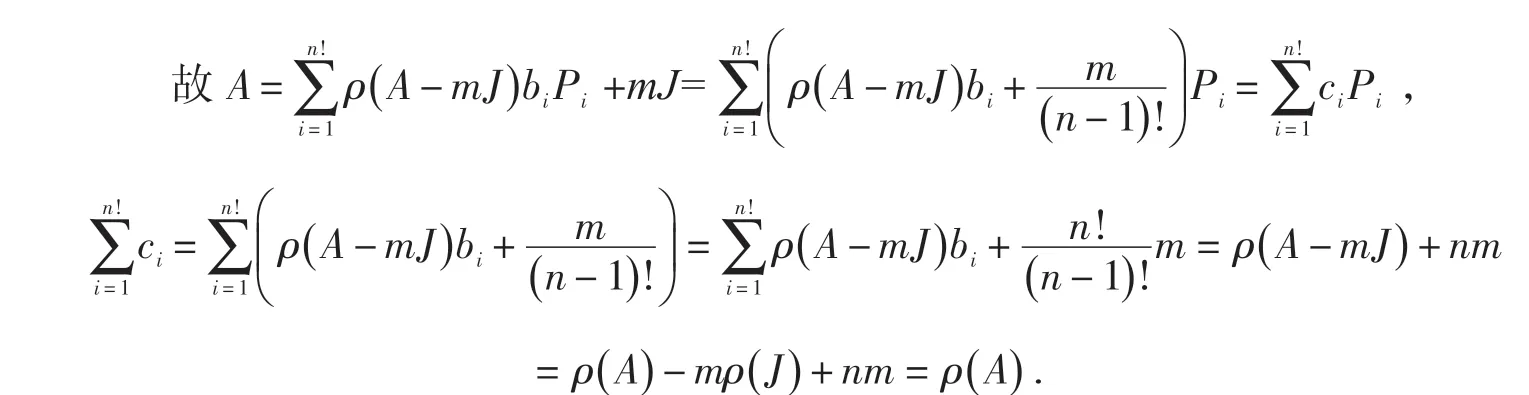
定理5 设A ∈Rn×n，若A 是可约的非负准幻方矩阵，且准幻方和值为ρ(A)，则存在n 阶置换矩阵P，使得PAPT=A1⊕A2⊕…⊕Ap， 其 中 Ai为 ni阶 非 负 准 换 方 矩 阵 且 ρ(Ai)=ρ(A) (i=1,2,…p,n1+n2+…+np=n).即，n 阶可约的非负准幻方矩阵A 置换相似于准幻方和值都为ρ(A) 的非负准幻方矩阵Ai(i=1,2,…p）的直和，其中n1+n2+…+np=n.

证明 设A 为可约的非负准幻方矩阵，当ρ(A) =0时，A=0，显然定理成立；当ρ(A) ≠0时，则为可约的双随机矩阵，由引理5可知则存在n 阶置换矩阵P，使得其中 Bi为ni阶 双 随 机 矩 阵(i=1,2,…p, n1+n2+…+np=n) ， 等 式 两 边 同 时 乘 以 ρ()A 得PAPT=ρ(A)B1⊕ρ(A)B2⊕…⊕ρ(A)Bp（n1+n2+…+np=n).

令Ai=ρ(A)Bi(i=1,2,…p ），则 有PAPT=A1⊕A2⊕…⊕Ap，且 ρ(Ai)=ρ(A) (i=1,2,…p ）， Ai(i=1,2,…p）都是非负准幻方矩阵.

即，n 阶可约的非负准幻方矩阵A 置换相似于准幻方和值都为的非负准幻方矩阵ρ()A 的直和，

其中Ai(i=1,2,…p）.得证.

[1]陈景良，陈向晖.特殊矩阵[M].北京：清华大学出版社，2003.

[2]戴华.矩阵论[M].北京：科学出版社，2001.

[3]BIRKHOFF G.Tres observaciones sobre el algebra lineal[J].Univ.Nac.Tucuman Rev.Sor.A，1946，5：147-150.

[4]汪潘义.奇数阶幻方矩阵的一个对称性质及其证明[J].零陵学院学报，2010（1）：78-79.

[5]刘玉，郑晓周.准幻方矩阵及其性质[J].邵阳学院学报，2012，9（3）：14-17.

[6]刘玉，郑晓周.准幻方矩阵及其判定[J].南通大学学报，2012，11（4）：86-89.

[7]徐金生.关于不可约矩阵定义的等价性及其应用[J].山西大学学报，1983（2）：14-22.

[8]XU Changqing,LI Jiongsheng.A Note On Completely Positive Matrices[J].Sy stem.Sci.Math，2000（13），21-25.