基于微分算子的局部特征尺度分解方法及其应用

吴占涛　程军圣　李宝庆　郑近德

1. 湖南大学汽车车身先进设计制造国家重点实验室，长沙，4100822.安徽工业大学，马鞍山，243032

基于微分算子的局部特征尺度分解方法及其应用

吴占涛1程军圣1李宝庆1郑近德2

1. 湖南大学汽车车身先进设计制造国家重点实验室，长沙，4100822.安徽工业大学，马鞍山，243032

针对局部特征尺度分解(LCD)方法在目标信号所含频率分量较接近时分解能力降低，易出现模态混淆现象，从而导致内禀尺度分量失去原有物理意义的问题，提出了基于微分算子的局部特征尺度分解(DOLCD)。DOLCD在对目标信号进行分解前，先将目标信号进行一阶微分，则在频率比一定的情况下，可提升分解能力及抑制模态混淆能力。研究了DOLCD方法的原理，通过仿真信号模型将DOLCD与LCD的分解能力进行对比分析，结果表明，DOLCD方法在提高分解能力，抑制模态混淆等方面具有一定的优越性，并将DOLCD方法应用于转子不对中故障的诊断，结果表明该方法有效。

局部特征尺度分解；微分算子；故障诊断；内禀尺度分量；转子

0　引言

经验模态分解(empirical mode decomposition,EMD)是一种自适应的非平稳信号处理方法[1-2]，EMD方法自提出后在很多领域得到了广泛的应用[3]。然而，EMD方法存在包络过冲和欠包络、迭代计算量大、端点效应以及模态混淆等问题[4]。作为对EMD方法的改进，程军圣等[5]提出了另一种自适应时频分析方法——局部特征尺度分解(local characteristic-scale decomposition, LCD)。LCD能够自适应地将一个复杂信号分解为若干个瞬时频率具有物理意义的内禀尺度分量(intrinsic scale component，ISC)之和，从而得到目标信号完整的时频分布。与EMD相比，LCD在减小拟合误差、提高计算速度和抑制模态混淆等方面有一定优势，已被应用于信号分析和机械故障诊断等领域，取得了较好的效果[6-7]。LCD方法理论基础尚不完善，实际应用中难免出现模态混淆现象，即同一尺度或频率的信号被分解到多个不同的ISC分量当中，或者一个ISC分量当中出现了尺度或频率差异较大的信号，降低了LCD方法的分解能力，导致分解得到的ISC分量失去原有的物理意义。

为解决LCD的模态混淆问题，郑近德等[8]基于向目标信号中成对地添加符号相反的白噪声信号，对加噪信号依据频率高低逐层进行集成平均分解的思路，提出了部分集成局部特征分解(partly ensemble local characteristic-scale decomposition，PELCD)方法。PELCD对LCD分解中的模态混淆有很好的抑制作用，但由于PELCD不能自适应地选择添加白噪声的幅值和数目，若参数选择不合适，可能会产生伪分量。本文从另一种思路，解决LCD模态混淆问题。

改变目标信号中低频分量与高频分量的幅值比，可提升LCD方法的分解能力，进而有效抑制模态混淆的产生。借鉴刘海波等[9]在对EMD改进时提出的利用微分算子增强EMD分解能力的思路，在对目标信号进行LCD分解前，先将目标信号进行一阶微分，则在频率比一定的情况下，可降低低频分量信号与高频分量信号的幅值比，提升LCD方法的分解能力及抑制模态混淆能力。基于此，笔者提出了基于微分算子的局部特征尺度分解(differential operator based local characteristic-scale decomposition, DOLCD)。

本文研究了DOLCD方法的原理，通过仿真信号将DOLCD与LCD的分解能力进行对比分析，结果表明，DOLCD方法分解能力范围要明显大于LCD方法的分解能力范围，增强了抑制模态混淆能力。采用DOLCD方法对具有不对中故障的转子振动位移信号进行了分析，结果表明DOLCD能够有效地将高频不对中成分与转频成分等进行分离，从而实现转子故障诊断。

1　DOLCD方法

杨宇等[10]对LCD方法的分解能力从理论层面上进行了深入研究。研究结果表明LCD方法的分解能力主要由各分量信号的频率比、幅值比决定，在频率比一定的情况下，降低低频分量信号与高频分量信号幅值比，可提高LCD方法的分解能力，抑制模态混淆；而各分量信号的初始相位以及单个分量迭代次数对LCD方法的分解能力影响均不大。为提高LCD方法的分解能力，抑制模态混淆，本文提出了基于微分算子的局部特征尺度分解方法。对目标信号x(t)(t>0)，DOLCD方法的主要分解步骤如下：

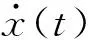
(3)对y1(t)进行积分，得到z1(t)。

(4)对z1(t)进行LCD分解，得到目标信号x(t)的第一个有效ISC分量I1(t)与剩余信号r1(t)。

(5)将分量I1(t)与目标信号x(t)分离，得到剩余信号s1(t)，即

s1(t)=x(t)-I1(t)

(1)

再将s1(t)视为目标信号，重复上述步骤(1)～(5)，直到sn(t)为单调或常函数，依次得到ISC分量I1(t)，I2(t)，…，In(t)和趋势项r1(t)，r2(t)，…，rn(t)。令

R(t)=r1(t)+r2(t)+…+rn(t)

(2)

(6)原目标信号x(t)被分解为n个ISC分量和一个趋势项R(t)之和，即

(3)

由于信号的初始相位对LCD的分解能力影响不大，为了讨论方便、不失一般性，设输入目标信号x(t)由两种模态构成，即

x(t)=x1(t)+x2(t)=A1sin(2πf1t)+A2sin(2πf2t)

(4)

其中，f1>f2。低频分量信号x2(t)与高频分量信号x1(t)的频率比F为

F=f2/f1

(5)

低频分量信号x2(t)与高频分量信号x1(t)的幅值比a为

a=A2/A1

(6)

对式(4)两边进行一阶微分得

2πf2A2cos(2πf2t)

(7)

b=(f2/f1)(A2/A1)

(8)

由于f1>f2，则b

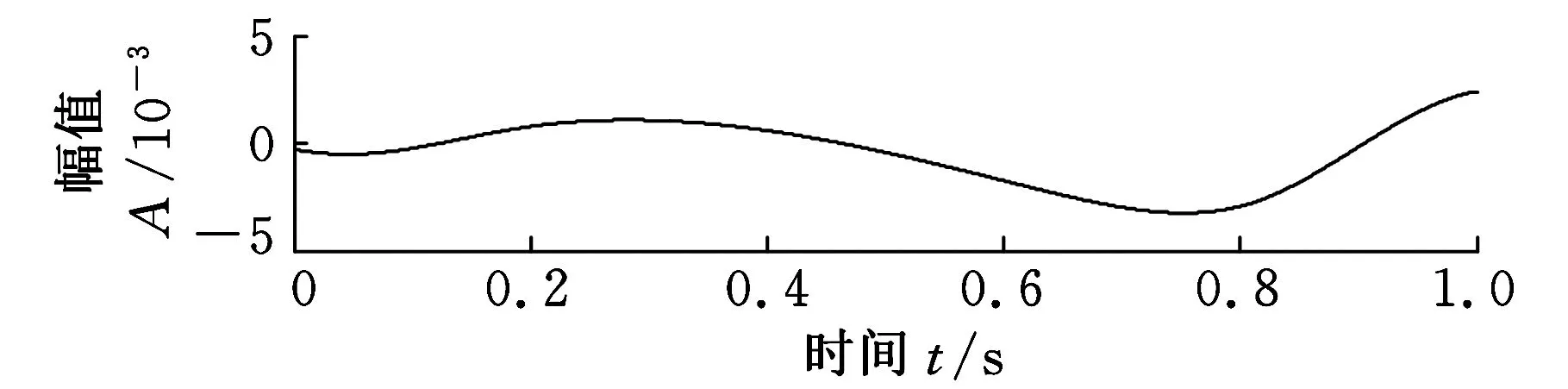
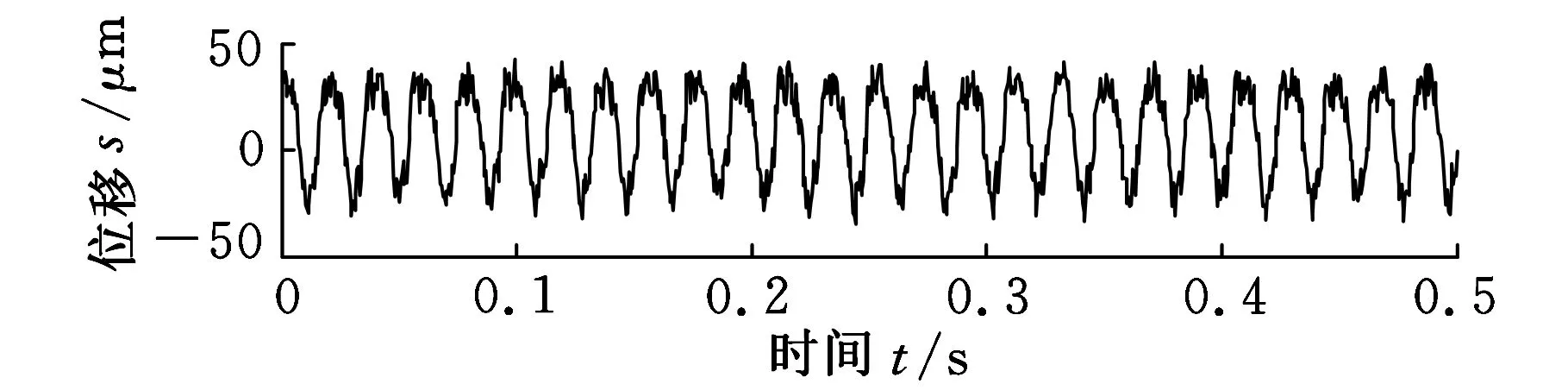
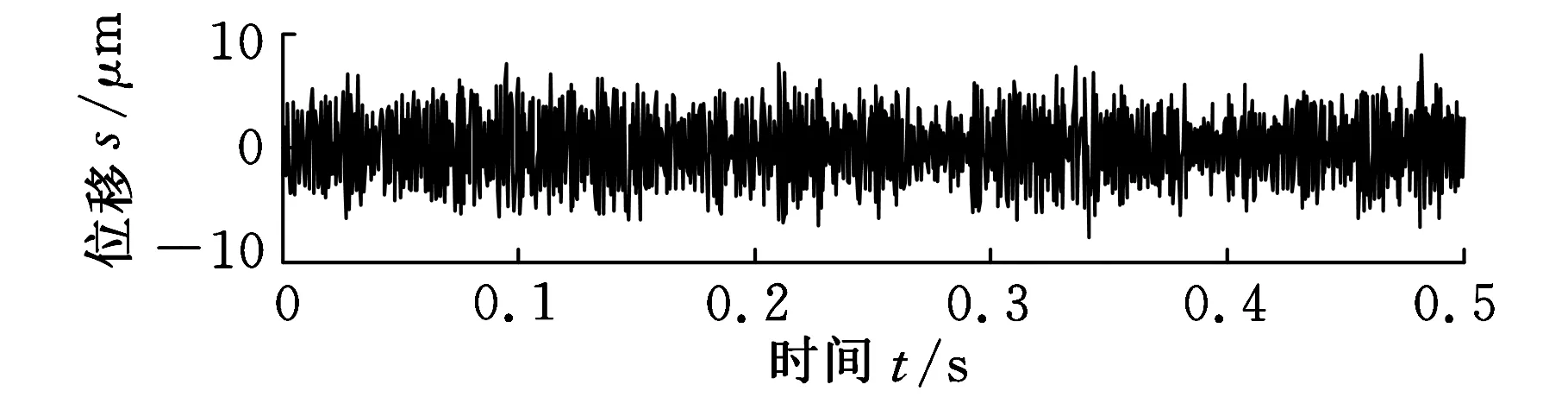
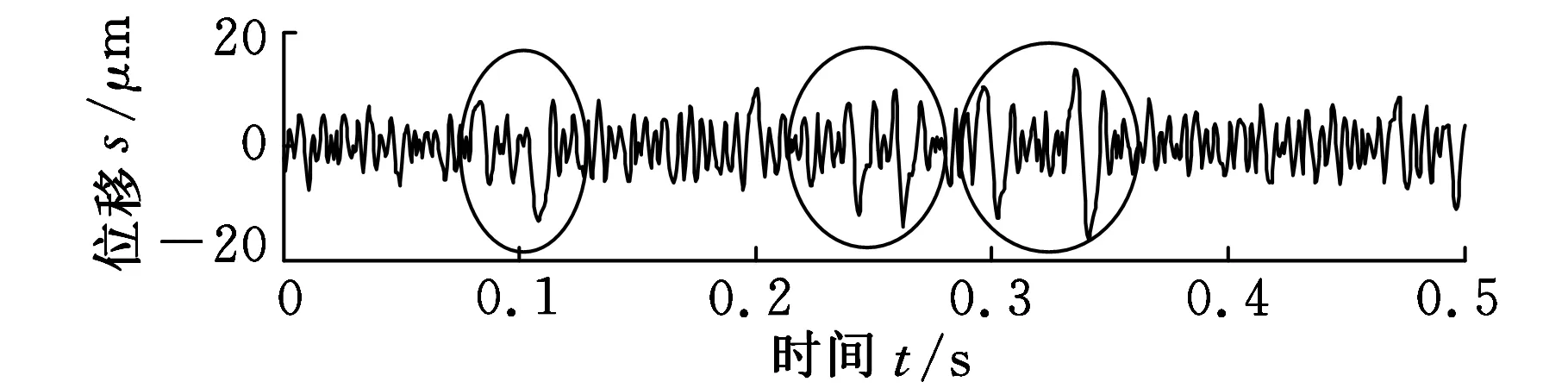
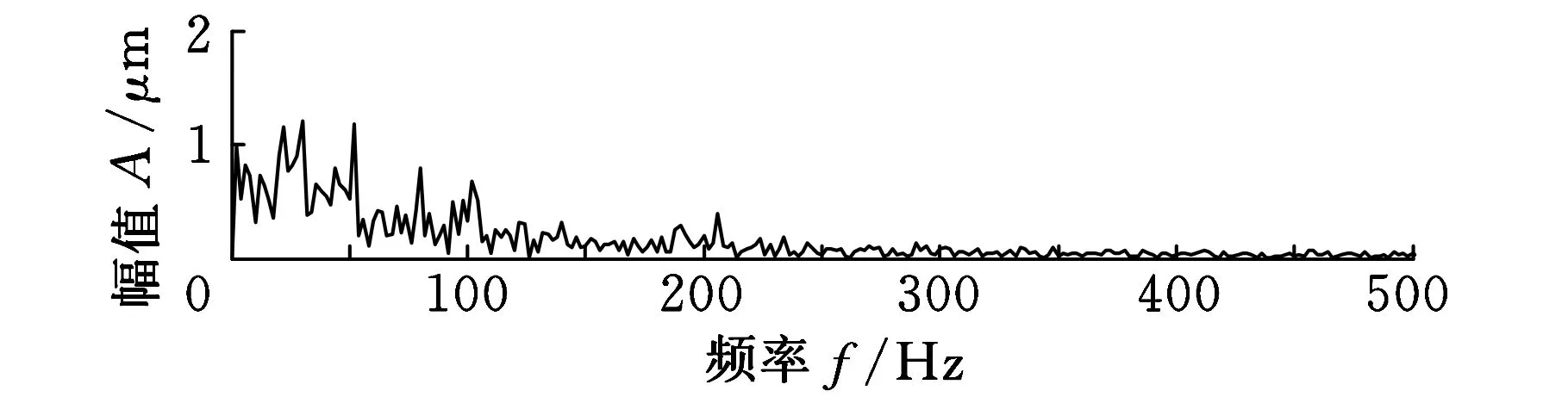
2　DOLCD分解能力

2.1分解能力评估模型与评价指标

为了评价DOLCD方法的分解能力，需确定一个分解能力的评价指标。参考文献[10]定义式(9)为分解能力评价指标(evaluationindexofdecompositioncapacity)，记为E：

(9)

式中，xi(t)为单分量信号的真实值；Ii(t)为分解得到的单分量信号；T为信号长度。

为了保证分解得到的分量全部准确，分解能力评价指标由下式确定：

E=max[Ei]

(10)

由于式(10)可能出现E>1的情况，为了便于研究，对E>1的情况，则令E=1，即E∈[0,1]。E值越大说明分解得到的Ii(t)越偏离真实分量xi(t)，分解能力越弱；E值越小说明分解得到的分量Ii(t)越接近于真实分量xi(t)，分解能力越强。文献[10-11]研究表明，当E≤0.05时，可认为混合信号被准确分解。

2.2分解能力对比

为了不失一般性，仍采用式(4)所示的信号模型为分析对象，并设A1=4，f1=80，频率比F∈[0.1,1]，幅值比a∈[0.1,∞]，信号采样频率fs=8192Hz。则在不同的幅值比a、频率比F条件下得到DOLCD方法的分解能力评价指标E值如图1所示。

图1　幅值比a和频率比F对E值的影响

由图1可以看出，当a大致满足a<1.1时，E值曲面形成一个坡面，该坡面在0.1≤F<0.7的部分较为平坦，此时E≤0.05；随着F增大，坡面逐渐变陡，在F接近1的部分坡面又变得相对平坦，但E值接近1。当a>1.1，F≤0.37时，E值曲面也较平坦，此时E≤0.05。当a>1.1，F>0.37时，随着F增大，会出现非常陡峭的曲面。

当E≤0.05时，表示DOLCD方法具有较好的分解效果，此时可认为两个分量信号能够被有效分离。当0.05

图2　DOLCD方法分解能力

由图2可以看出，E=1和E=0.05两条等高线将整个a-F平面划分为3个区域：Ⅰ区为E=1区域，表示DOLCD方法完全不能将两个单分量分离；Ⅱ区为0.05

采用LCD方法对式(4)所示的信号模型进行分解，运行参数与图2相同，其分解能力区域分布图如图3所示。参照图2，绘制E值分别为0.05和1的两条等高线，将a-F平面划分为3个区域。与图2对比可以发现，图3中的区域Ⅲ明显小于图2中的区域Ⅲ。表明在相同的采样频率fs、最大频率fmax和相同最大迭代次数等运行条件下，DOLCD方法分解能力范围要明显大于LCD方法的分解能力范围，增强了抑制模态混淆的能力。

图3　LCD方法分解能力

2.3分解能力的影响因素

需要说明的是，图3所示的LCD分解能力图与文献[10]有所差异，这主要是因为信号模型的采样频率fs，以及fs与最大频率fmax的关系对LCD分解效果的影响。图2和图3中，采样信号模型的采样频率fs=8192Hz，高频分量信号最大频率fmax=80Hz。仍采用式(4)所示的信号模型，分别更改信号模型的采样频率fs和最大频率fmax，分析DOLCD方法和LCD方法的分解能力。当fs=4096Hz，高频分量信号最大频率fmax=80Hz时，以及当fs=8192Hz，高频分量信号最大频率fmax=200 Hz时，DOLCD方法和LCD方法的分解能力分别如图4a、图4c和图4b、图4d所示。

对图4分析可得，尽管图4a和图4c的区域Ⅲ与图2中的区域Ⅲ，以及图4b和图4d的区域Ⅲ和图3中的区域Ⅲ均有所不同，但图4a和图4c的区域Ⅲ均明显大于图4b和图4d的区域Ⅲ。这也说明了DOLCD方法的分解能力要强于LCD方法。

3　仿真分析与应用实例

3.1仿真分析

为了说明DOLCD方法的优越性、不失一般性，仍采用式(4)所示的信号模型为分析对象，其中A1=2，A2=18，f1=16，f2=4，即x(t)=2sin(32πt)+18sin(8πt)，t∈[0,1]，其时域波形如图5所示。

(a)fs=4096 Hz、fmax=80 Hz时，DOLCD方法的分解能力

(b)fs=4096 Hz、fmax=80 Hz时，LCD方法的分解能力

(c)fs=8192 Hz、fmax=200 Hz时，DOLCD方法的分解能力

(d)fs=8192 Hz、fmax=200 Hz时，LCD方法的分解能力图4　两组不同运行参数对应的两种方法的分解能力

(a)仿真信号x1(t)

(b)仿真信号x2(t)

(c)仿真信号x(t)图5　仿真信号x(t)及其各成分的时域波形

信号x(t)是一个大幅值的低频信号与小幅值的频率略高信号的叠加信号，其幅值比a=A2/A1=9，频率比F=f2/f1=0.25。根据对图3的分析，信号x(t)处于图3的区域Ⅰ，LCD无法将信号x(t)的两分量有效分离。对图6所示信号x(t)的LCD分解结果分析可得，LCD分解得到第一个分量I1(t)与目标信号x(t)的幅值、频率均区别不大；第二个分量I2(t)的幅值很小，从其时域图上无法看出有物理意义的频率成分。对其第一个分量I1(t)的幅值谱(图7)进行分析，可明显看出分量I1(t)包含了目标信号x(t)的两种频率成分。可见采用LCD对信号x(t)进行分解时，第一个ISC分量I1(t)中包含有频率差异较大的不同信号成分，出现了严重的模态混淆，LCD未能实现对仿真信号x(t)的有效分解，这与前面的分析是一致的。

(a)第一个ISC分量I1(t)

(b)第二个ISC分量I2(t)

(c)剩余项R2(t)图6　仿真信号x(t)的LCD分解结果

图7　LCD分解信号x(t)得到的分量I1(t)的幅值谱

对图2进行分析，信号x(t)处于图2中区域Ⅲ，采用DOLCD可有效实现信号x(t)的两分量分离，信号x(t)的DOLCD的分解结果如图8所示。

(a)第一个ISC分量I1(t)

(b)第二个ISC分量I2(t)

为了进一步比较两种方法的分解效果，论文还对两种方法得到的两分量与对应真实分量的相关系数[11]进行了对比，相关系数指标值越大，表示分解的准确性越高。DOLCD得到的两分量的相关系数指标值为0.9999和1，LCD得到的两分量的相关系数指标值为0.1104和0.1713。这说明与LCD方法相比，DOLCD方法在分解精确度方面表现出一定的优越性。

3.2应用实例

为了进一步说明DOLCD方法的有效性与实用性，论文将其应用于不对中故障[12]的转子振动位移实验信号分析。实验装置如图9所示，转子转速为3000 r/min，转频fr=50 Hz，实验采样频率fs=2048 Hz，采样时长为0.5 s。实验数据的时域波形如图10所示。其幅值谱如图11所示。采用刚性联轴器连接的转子不对中时，强制连接所产生的力矩，使转子发生弯曲变形；转轴内阻以及转轴表面与旋转体内表面之间的摩擦而产生的相对滑动，使转子产生自激旋转周期性振动，其振动频率为转子转频fr的2倍，常伴频率为转频fr的1倍频，转子振动位移信号会产生一个以转频为幅值调制频率的高频分量[13]。由图10可以看出，高频的分量信号被淹没在强大的背景信号中。从图11中主要看到的是与转频fr相关的基频分量，看不出不对中故障信息。为提取高频不对中故障信息，分别采用DOLCD和LCD对实验数据进行分解，分解结果如图12和图13所示，限于篇幅只画出前三个分量。

图9　转子实验装置示意图

图10　实验数据的时域波形

图11　实验数据的幅值谱

(a)第一个ISC分量I1(t)

(b)第二个ISC分量I2(t)

(c)第三个ISC分量I3(t)图12　实验数据的DOLCD分解结果

(a)第一个ISC分量I1(t)

(b)第二个ISC分量I2(t)

(c)第三个ISC分量I3(t)图13　实验数据的LCD分解结果

由图12可以看出，DOLCD方法对实验数据分解得到的第一个分量I1(t)是高频背景噪声信号，第二个分量I2(t)具有明显的调制特征，包含了主要故障信息，分量I3(t)是与转频有关的背景信号。从图13中可以看出，LCD方法对实验数据分解得到的第一个分量I1(t)也是高频背景噪声信号，第二个分量I2(t)也能看出调制特征，第三个分量I3(t)是与转频有关的背景信号；但分量I2(t)和I3(t)均出现了严重的波形失真和模态混淆(如图中实线所圈部分)。采用希尔伯特变换(Hilbert transform, HT)分别估计两种方法得到的第二个分量的包络谱，结果分别如图14和图15所示。

图14　DOLCD的分量I2(t)的包络谱

图15　LCD的分量I2(t)的包络谱

由图14所示的DOLCD分量I2(t)的包络谱图可以看到明显的转频fr的2倍频和转频fr的1倍频，这与转子发生不对中故障时的频率特征相吻合[14]。图15所示的LCD分量I2(t)的包络谱图中未出现明显的转频fr的2倍频，无法有效识别实验数据所包含的故障类型。

对上述实验数据分析说明，相对LCD方法，DOLCD能更为有效地将高频不对中信号从强大的背景信号中提取出来，实现不对中故障信号、背景信号和噪声信号的分离，从而实现转子故障诊断，同时也有效抑制了模态混淆。

4　结论

(1)采用仿真信号模型将DOLCD与LCD分解能力进行对比分析，发现DOLCD方法分解能力范围要明显大于LCD方法的分解能力范围，分解结果准确性更高，也有效地抑制了模态混淆。

(2)将DOLCD方法应用于转子不对中故障信号的分析，分解得到了高频调制特征分量和低频分量，有效地实现了转子不对中故障的诊断。

论文提出的DOLCD方法不需要事先选择基函数，是一种自适应的信号分析方法，可有效地应用于机械设备故障诊断。本文仅是简单的从信号模型两组不同的采样频率和最大频率对两种方法分解能力的影响进行了对比分析。笔者后续将进一步对信号模型不同的运行参数对LCD分解能力的影响进行系统性的研究。

[1]Huang N E, Shen Z, Long S R,et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.

[2]Huang N E, Wu Z.A Review on Hilbert Huang Transform: Method and Its Applications to Geophysical Studies[J]. Reviews of Geophysics, 2008, 47(2): 1-23.

[3]Lei Yaguo, Lin Jing, He Zhengjia, et al. A Review on Empirical Mode Decomposition in Fault Diagnosis of Rotating Machinery[J]. Mechanical Systems and Signal Processing, 2013, 35(1): 108-126.

[4]时培明, 蒋金水, 刘彬, 等. 基于边界特征尺度匹配延拓的EMD改进方法及应用[J]. 中国机械工程, 2014，25(12): 1616-1623.

Shi Peiming, Jiang Jinshui, Liu Bin, et al. Improved Method of EMD and Its Applications Based on Boundary Characteristic Scale Matching Extension Method[J]. China Mechanical Engineering, 2014，25(12): 1616-1623.

[5]程军圣, 郑近德, 杨宇. 一种新的非平稳信号处理方法——局部特征尺度分解法[J]. 振动工程学报, 2012, 25(2): 215-220.

Cheng Junsheng, Zheng Jinde, Yang Yu. A Nonstationary Signal Analysis Approach——the Local Characteristic-scale Decomposition Method[J]. Journal of Vibration Engineering, 2012, 25(2): 215-220.

[6]Zheng Jinde, Cheng Junsheng, Yang Yu. Generalized Empirical Mode Decomposition and Its Applications to Rolling Element Bearing Fault Diagnosis[J]. Mechanical Systems and Signal Processing, 2013, 40(1): 136-153.

[7]郑超, 郭奇, 郭丽杰, 等. 基于局部特征尺度分解的旋转机械故障欠定盲源分离方法研究[J]. 燕山大学学报, 2014, 38(2): 168-174.

Zheng Chao, Guo Qi, Guo Lijie, et al. Underdetermined Blind Source Separation Method of Rotating Machinery Faults Based on Local Characteristic-scale Decomposition[J]. Journal of Yanshan University, 2014, 38(2):168-174.

[8]郑近德, 程军圣, 杨宇. 部分集成局部特征尺度分解：一种新的基于噪声辅助数据分析方法[J]. 电子学报, 2013, 41(5): 1130-1135.

Zheng Jinde, Cheng Junsheng, Yang Yu. Partly Ensemble Local Characteristic-scale Decomposition: A New Noise Assisted Data Analysis Method[J]. Acta Electronica Sinica, 2013, 41(5): 1130-1135.

[9]刘海波, 玄志武. 利用微分算子增强EMD算法频带分解能力[J]. 振动与冲击, 2013, 32(18): 133-135.

Liu Haibo, Xuan Zhiwu. Improving Frequency-band Separating Ability of EMD with a Differential Operator[J]. Journal of Vibration and Shock, 2013, 32(18): 133-135.

[10]杨宇, 曾鸣, 程军圣. 局部特征尺度分解方法及其分解能力研究[J]. 振动工程学报, 2012, 25(5): 602-609.

Yang Yu, Zeng Ming, Cheng Junsheng. Research on Local Characteristic-scale Decomposition and Its Capacities[J]. Journal of Vibration Engineering, 2012, 25(5):602-609.

[11]Rilling G, Flandrin P. One or Two Frequencies? The Empirical Mode Decomposition Answers[J]. IEEE Transactions on Signal Processing, 2008, 56(1): 85-95.

[12]孙斌, 刘立远, 雷伟. 基于正交局部保持映射的转子故障诊断方法[J]. 中国机械工程, 2014, 25(16): 2219-2224.

Sun Bin, Liu Liyuan, Lei Wei. Rotor Fault Diagnosis Method on Orthogonal Locality Preserving Projection[J]. China Mechanical Engineering, 2014, 25(16): 2219-2224.

[13]盛兆顺, 尹琦岭. 设备状态监测与故障诊断技术及应用[M]. 北京: 化学化工出版社, 2003.

[14]刘杨, 太兴宇, 姚红良, 等. 双盘转子轴承系统不对中-碰摩耦合故障分析[J]. 振动、测试与诊断, 2013, 33(5): 819-823.

Liu Yang, TaiXingyu, Yao Hongliang, et al. Study on Misalignment-rubbing Coupling Fault of Dual-disk Rotor-bearing System Including the Impact of Motor Coupling[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(5): 819-823.

(编辑王旻玥)

Local Characteristic-scale Decomposition Method Based on Differential Operator and Its Applications

Wu Zhantao1Cheng Junsheng1Li Baoqing1Zheng Jinde2

1.State key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University,Changsha,410082 2.Anhui University of Technology,Ma’anshan,Anhui,243002

A novel non-stationary signal method differential operator based LCD(DOLCD) was proposed for improving the LCD method, of which, when the target signal contained components with frequencies close to each other, the decomposition ability was decreased, mode mixing phenomenon would easily occur and the physical meaning of intrinsic scale components decomposed were lost. A differential operator was used to differentiate the target signal in time domain, then the differentiated target signal was decomposed with DOLCD, then in the certain frequency ratio, the decomposition ability was enhanced, and the mode mixing was inhibited. The paper firstly studied the theory of DOLCD, then simulation experiments were used to compare the decomposition ability of DOLCD with LCD. The results indicate that DOLCD is more efficient in improving the decomposition ability, and inhibiting the mode mixing than LCD. Finally, the proposed method was applied to diagnose the rotor with misalignment faults successfully which indicated the effectiveness of DOLCD.

local characteristic-scale decomposition(LCD); differential operator; fault diagnosis; intrinsic scale component(ISC); rotor

2015-03-15

国家自然科学基金资助项目(51375152)；湖南省科技计划资助项目(2014WK3005)

TH165.3；TH911.7DOI：10.3969/j.issn.1004-132X.2015.17.003

吴占涛，男，1982年生。湖南大学机械与运载工程学院博士研究生。主要研究方向为动态信号处理及机械设备故障诊断。程军圣(通信作者)，男，1968年生。湖南大学机械与运载工程学院教授、博士、博士研究生导师。李宝庆，男，1984年生。湖南大学机械与运载工程学院博士研究生。郑近德，男，1986年生。安徽工业大学机械工程学院讲师、博士。