基于DEMD和对称差分能量算子解调的滚动轴承故障诊断

孟　宗　季　艳

河北省测试计量技术及仪器重点实验室(燕山大学)，秦皇岛，066004

基于DEMD和对称差分能量算子解调的滚动轴承故障诊断

孟宗季艳

河北省测试计量技术及仪器重点实验室(燕山大学)，秦皇岛，066004

针对机械故障振动信号多为调制信号的特点，为了更好地提取多分量调幅调频信号的幅值和频率信息，提出了基于微分的经验模式分解(DEMD)与对称差分能量算子相结合的解调方法。利用DEMD算法将原始振动信号进行分解，得到若干个单分量信号；对每一个单分量信号进行三点对称差分能量算子解调，得到各单分量信号的瞬时幅值和瞬时频率，并计算出包络谱。将该方法应用于仿真信号和滚动轴承故障信号的诊断，实验结果表明，该方法能有效地提取机械故障信号的故障特征，实现旋转机械故障诊断。

微分经验模式分解；对称差分能量算子；滚动轴承；故障诊断

0　引言

滚动轴承是旋转机械设备的重要组成零部件之一，其运行状态的好坏直接关系到旋转设备的运行状态，因此对滚动轴承工作状况进行实时监测和故障诊断的研究越来越受到人们的重视[1]。故障特征提取是故障诊断过程的一个重要环节，同时也是目前制约故障诊断技术发展的主要瓶颈，直接关系到故障诊断的准确率和故障早期预报的可靠性。传统的故障特征提取方法通常是从时域或频域中反映信号的特性，无法同时兼顾信号在时域和频域的局部化特征和全貌。经验模式分解(empirical mode decomposition, EMD)方法[2]可将复杂的多分量信号自适应分解为一系列位于不同频带的本征模态函数(intrinsic mode function, IMF)之和，每一个IMF分量都是具有单一频率成分的波形信号，但EMD算法的频率分辨率有限，对于频率相近的信号，EMD算法很难分离出，会产生模态混叠现象。针对这一问题，文献[3]提出了一种基于微分的经验模式分解(differential-based empirical mode decomposition，DEMD)方法，该方法是对EMD分解算法的改进，在信号进行EMD分解前，对原信号进行微分运算，使信号的能量尽可能地按频率从高到低递减，进而能够有效分辨出不同频率成分，有效抑制模态混叠现象。当轴承发生故障时，故障信号通常以调制的形式出现，因此解调方法就成为了机械故障诊断中一种最为常用的方法[4]，常用的Hilbert变换的包络解调方法存在着误差较大等问题[5]，而Teager提出的能量算子法[6-8]具有更高的解调精度，但是，能量算子只适用于单分量的调幅调频信号，而大多数机械故障振动都是多分量的信号，所以一般都是先把信号分解成若干个单分量调幅调频信号，然后进行能量算子解调[9-11]。

本文将DEMD和对称差分能量算子解调算法相结合用于振动信号特征的提取，即首先对信号进行DEMD分解，得到若干个本征模态函数分量，然后对每一个分量进行三点对称差分能量算子解调，计算信号的瞬时幅值和瞬时频率，最后利用谱分析得出特征提取结果。

1　微分经验模态分解

DEMD算法在进行EMD处理前先对原始信号进行微分运算，然后再对各阶IMF分量进行积分还原信号。通过对原始信号进行微分，改变了信号中不同频率成分所占比重，增强EMD的频率分解能力，有利于将信号中相近的频率或微弱的高频成分提取出来，进一步改善EMD的模态混叠现象[12]。DEMD算法的步骤如下。

(1)对原信号x0(t)进行一次微分后再进行EMD分解，得到m个IMF分量，利用Hilbert变换解调方法判断分解后的IMF分量是否存在模态混叠现象。

(2)如果存在模态混叠现象，则对一次微分后的信号继续微分，然后进行EMD处理，直到微分n次后得到的xn(t)再进行EMD分解后，得到的m个IMF分量cni(t)(i=1,2,…,m)没有模态混叠现象为止，rn0(t)为分解过程中残余分量。

(3)对各阶IMF分量进行一次积分得

∫cni(t)dt=b(n-1)i(t)+b(n-1)i0

再对各b(n-1)i(t)进行一次EMD分解得

b(n-1)i(t)=c(n-1)i(t)+r(n-1)i(t)

(4)c(n-1)i(t)为原信号x0(t)微分n-1次后的IMF分量，残余分量为

(1)

(5)重复步骤(3)～步骤(4)，直到n次积分后获得原始信号的各阶IMF分量和残余分量：

(2)

信号经过微分处理能够使高频成分在信号中的振幅比重增加，进而使高频成分能量增加。故障信号往往存在高频部分，尤其是故障初期，故障信号的比重很小，很可能淹没于其他信号当中，不利于故障诊断。DEMD分解可以诊断出相对于主信号占比重很小的故障信号的存在，比传统的经验模态分解具有更好的故障识别能力。

2　对称差分能量算子解调方法研究

调频调幅信号

x(t)=a(t)cos(φ(t))=a(t)cos(ω(t)+θ)

(3)

对应的离散信号为

x(n)=a(n)cos(φ(n))=a(n)cos(ω(n)+θ)

(4)

对于信号x(t)，能量算子ψ定义为

ψ(x(t))=(x′(t))2-x(t)x″(t)

(5)

式(5)中的能量算子针对连续时间信号定义，对于离散时间信号x(n)，应用差分代替微分，则能量算子变为

ψ(x(n))=x2(n)-x(n-1)x(n+1)

(6)

一般来说，调制信号比载波信号变化要慢得多，即ψ(a(n))≈0，φ″(n)≈0。对离散信号x(n)进行非线性算子运算，得

ψ(x(n))=a2(n)sin2(ω(n))

(7)

对x(n)的向后差分信号y(n)=x(n)-x(n-1)进行能量算子计算求得ψ(y(n))后，得到信号的幅值a(n)和频率ω(n)的估计值：

(8)

(9)

传统能量算子解调方法在信号波形光滑度和频率值准确度方面还不尽如人意[13-15]，与Hilbert调制方法一样，瞬时幅值和瞬时频率在端点及突变点产生较大的波动，为此提出了对称差分能量算子解调方法。

对能量算子解调方法改进如下：

首先定义x(n)的差分序列为

(10)

为了提高解调结果的准确度，该差分序列就是在原离散信号基础之上进行了平滑处理。则y(n)的差分序列为

(11)

将式(10)和式(11)代入式(5)进行能量算子运算，得到改进的算子:

(12)

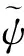
(13)

(14)

称该改进方法为对称差分能量算子解调法。

3　仿真分析

无论是能量算子解调还是对称差分能量算子解调，都只适用于单分量的调幅调频信号，而大多数的旋转机械故障振动信号都是多分量的调幅和调频信号，基于此，先采用DEMD方法把一个复杂的信号分解成若干个IMF分量之和，每一个IMF分量都可以是幅度或频率调制的单分量信号，再对每一个IMF分量进行对称差分能量算子解调，得到原始复杂信号的幅值和频率信息。

仿真信号为

y(t)=(1+0.5cos(15πt))cos(180πt+

2cos(6πt))+0.8sin(πt)sin(30πt)

(15)

仿真信号的波形图见图1，对仿真信号进行DEMD分解，得到图2所示分解结果，对IMF1、IMF2分量分别采用能量算子解调方法提取幅值和频率信息，得到的瞬时幅值和瞬时频率如图3所示。图4所示为采用对称差分能量算子解调法得到的各分量瞬时幅值和瞬时频率。

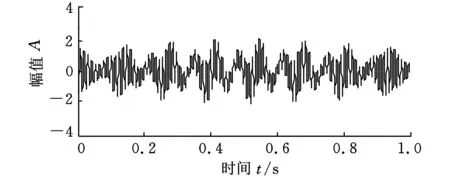
图1　仿真信号波形图

图2　DEMD分解结果

(a)IMF1分量的瞬时幅值

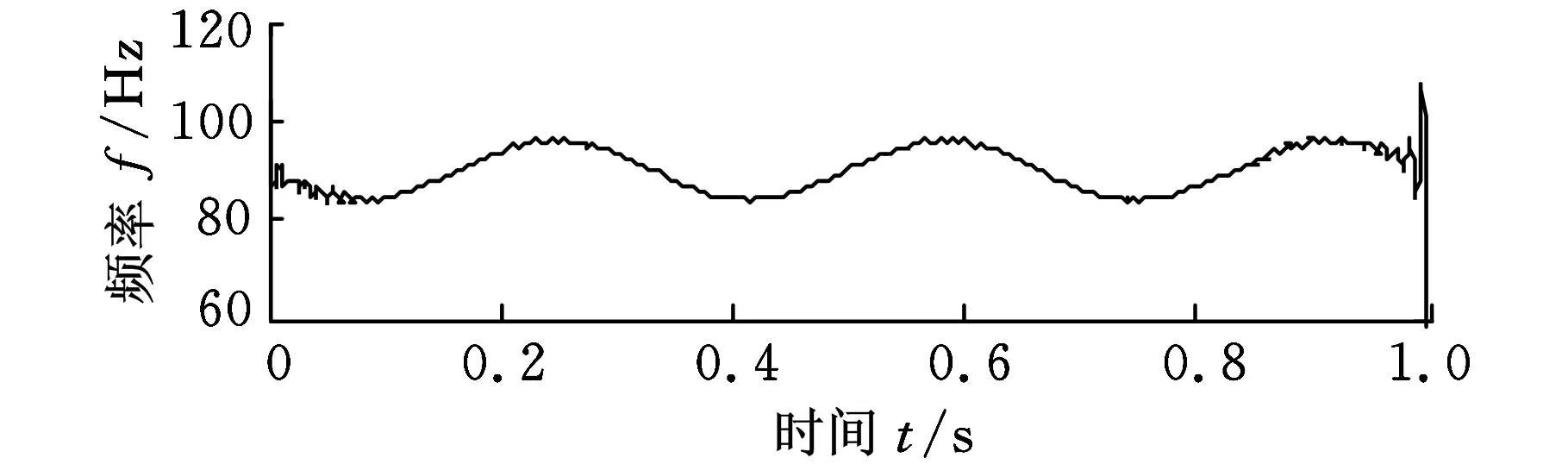
(b)IMF1分量的瞬时频率

(c)IMF2分量的瞬时幅值

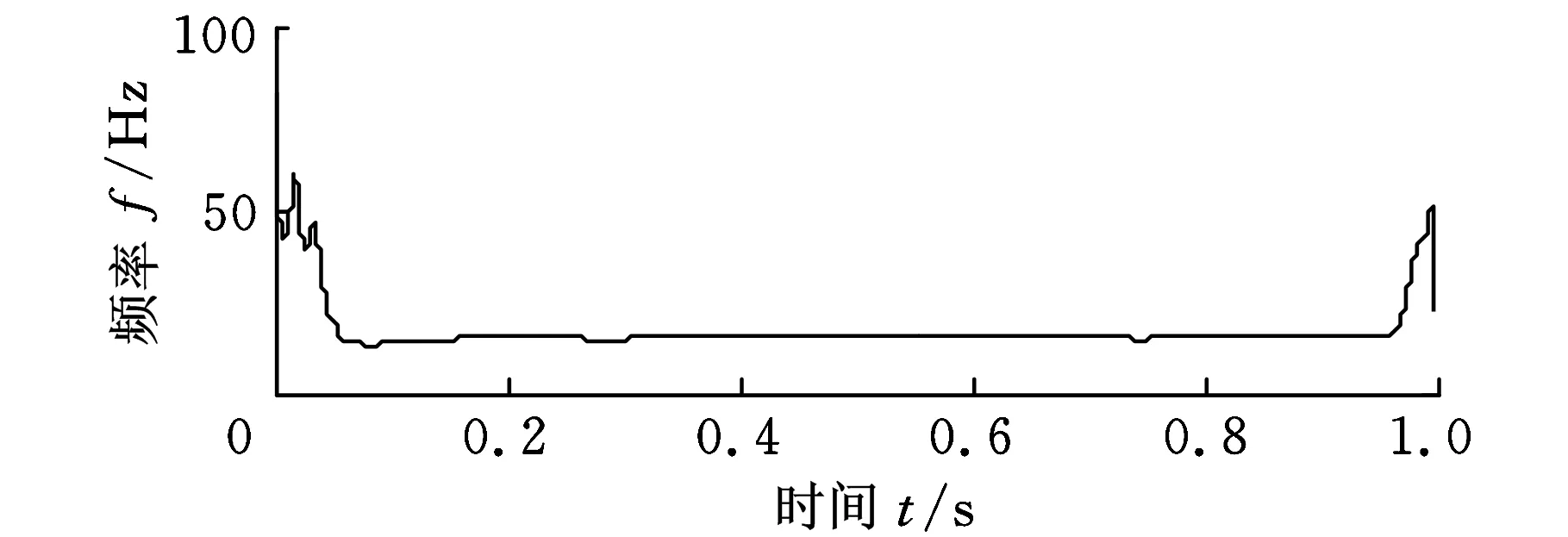
(d)IMF2分量的瞬时频率图3　能量算子解调后的瞬时幅值和瞬时频率

(a)IMF1分量的瞬时幅值

(b)IMF1分量的瞬时频率

(c)IMF2分量的瞬时幅值

(d)IMF2分量的瞬时频率图4　对称差分能量算子解调的瞬时幅值和瞬时频率

(a)IMF1分量包络谱

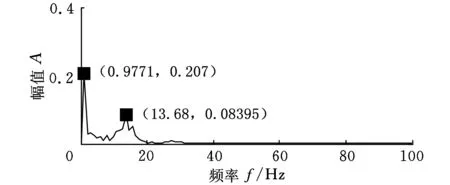
(b)IMF2分量包络谱图5　采用能量算子解调得到的包络谱

对比图3、图4可以看出，采用能量算子解调方法得到的瞬时幅值和瞬时频率曲线在两端仍出现波动，而且曲线并不十分光滑，说明在解调过程中产生了误差；经过对称差分能量算子解调得到的瞬时幅值和瞬时频率曲线波动减小，而且曲线波形更加平滑。对得到的信号进行频谱分析，得到包络谱如图5、图6所示，由图5可以看出，在7.816 Hz、0.9771 Hz和13.68 Hz处出现了峰值，这和设定的调幅频率7.5 Hz、 调幅频率0.5 Hz的二倍频和基频15 Hz值接近，但是没有提取出调幅调频分量的基频成分(90 Hz)，由图6a可以看出，采用对称差分能量算子解调后不仅出现了7.816 Hz的频率峰值，还出现了89.89 Hz的频率峰值，这与调幅频率7.5 Hz和基频90 Hz接近，误差分别为4.21%和0.12%，图6b中，采用对称差分能量算子解调得到IMF2分量的包络谱在0.9771 Hz和14.66 Hz出现了峰值，分别与调幅分量的调幅频率0.5 Hz的二倍频和基频15 Hz值接近，误差为2.29%和2.26%，误差小于能量算子解调得到频率误差。可见，基于DEMD和对称差分能量算子解调算法能够更加准确地提取出振动信号的特征频率。

(a)IMF1分量包络谱

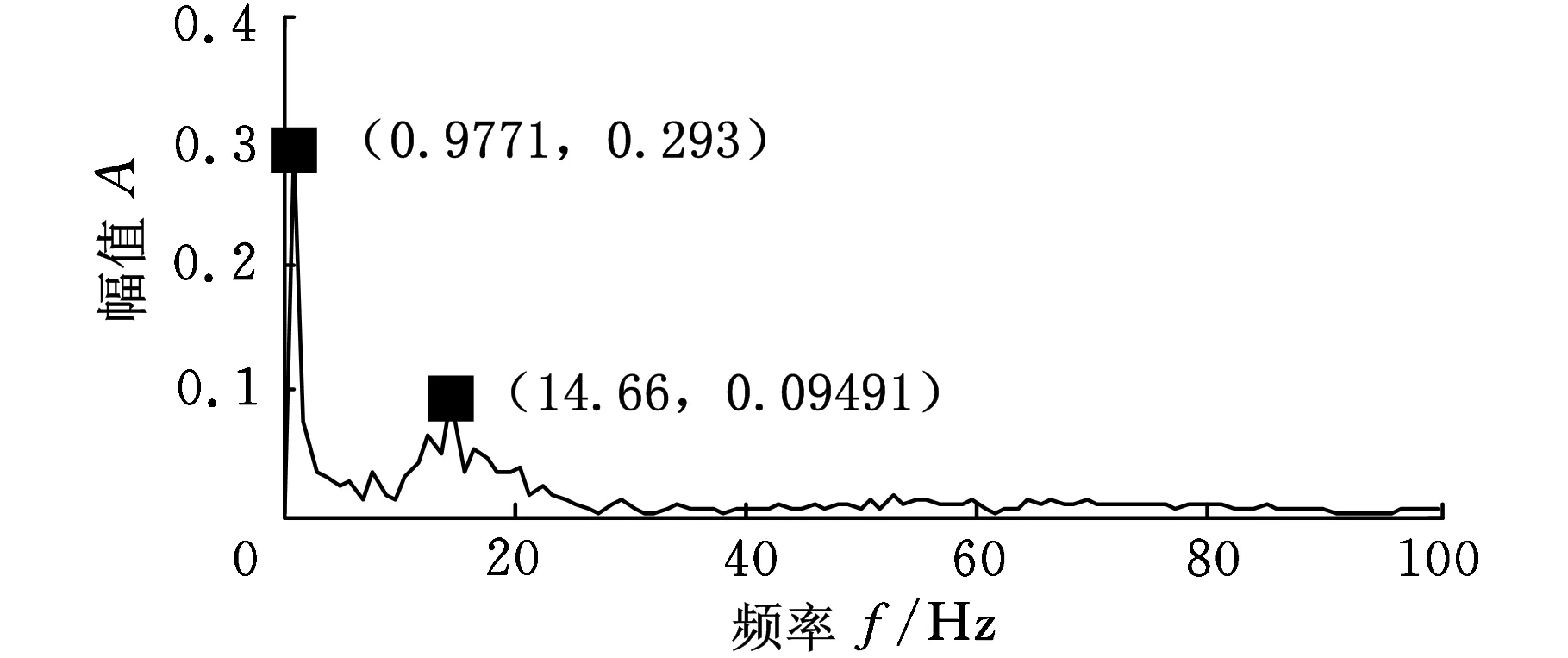
(b)IMF2分量包络谱图6　采用对称差分能量算子解调得到的包络谱

4　试验研究

本文对美国凯斯西储大学的滚动轴承振动数据进行试验研究及分析，以进一步验证提出的基于DEMD和对称差分能量算子解调方法的有效性。在试验装置中，1.5 kW的三相感应电机通过自校准联轴器与1个功率计和1个扭矩传感器相连，最后驱动风机进行运转，电机的负载由风机来调节。将电机轴的轴承作为待测轴承，待测的滚动轴承型号为SKF6205，使用电火花加工技术在轴承上布置了直径为0.1778 mm的单点故障。试验中电机的转速n为1750 r/min，则转轴基频为29.16 Hz，将振动加速度传感器垂直固定在感应电机输出轴支撑轴承上方的机壳上进行数据采集，采样频率为12 kHz，经过计算，滚动球轴承的内圈故障特征频率为157.94 Hz。采集轴承内圈故障状态下的振动信号，信号时域波形如图7所示，其包络谱如图8所示，图中只在54.69 Hz处存在明显谱线，这和计算得到的转轴基频的二倍频(58.32 Hz)接近，内圈故障频率和其二倍频均被淹没在其他频率信号中，不能被清晰地提取出来，故需对故障信号进行近一步处理。对原信号进行小波软阈值去噪处理，分解层数取5，阈值规则选择rigrsure规则。对消噪后的信号进行DEMD分解，图9中列出了分解后的前5个IMF分量。

图7　轴承内圈故障振动信号时域波形

图8　轴承内圈故障信号包络谱图

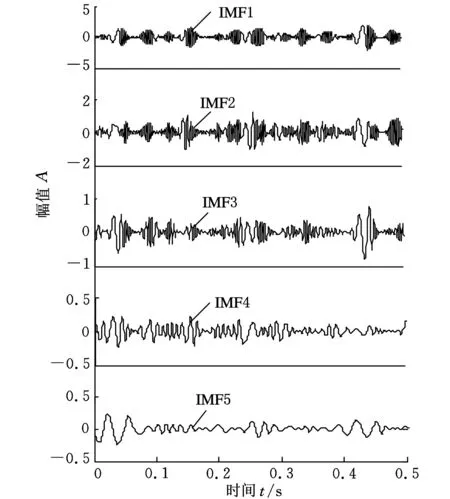
图9　轴承内圈故障信号DEMD分解图

从图9可以看出，由于随着DEMD分解的逐阶进行，各IMF分量的幅值越来越小，作为研究数据的价值越来越小，所以取幅值相对较大的IMF1和IMF2分量作为研究对象，采用能量算子解调法提取前两个IMF分量的瞬时幅值和瞬时频率，进一步进行频谱分析，其包络谱如图10所示。

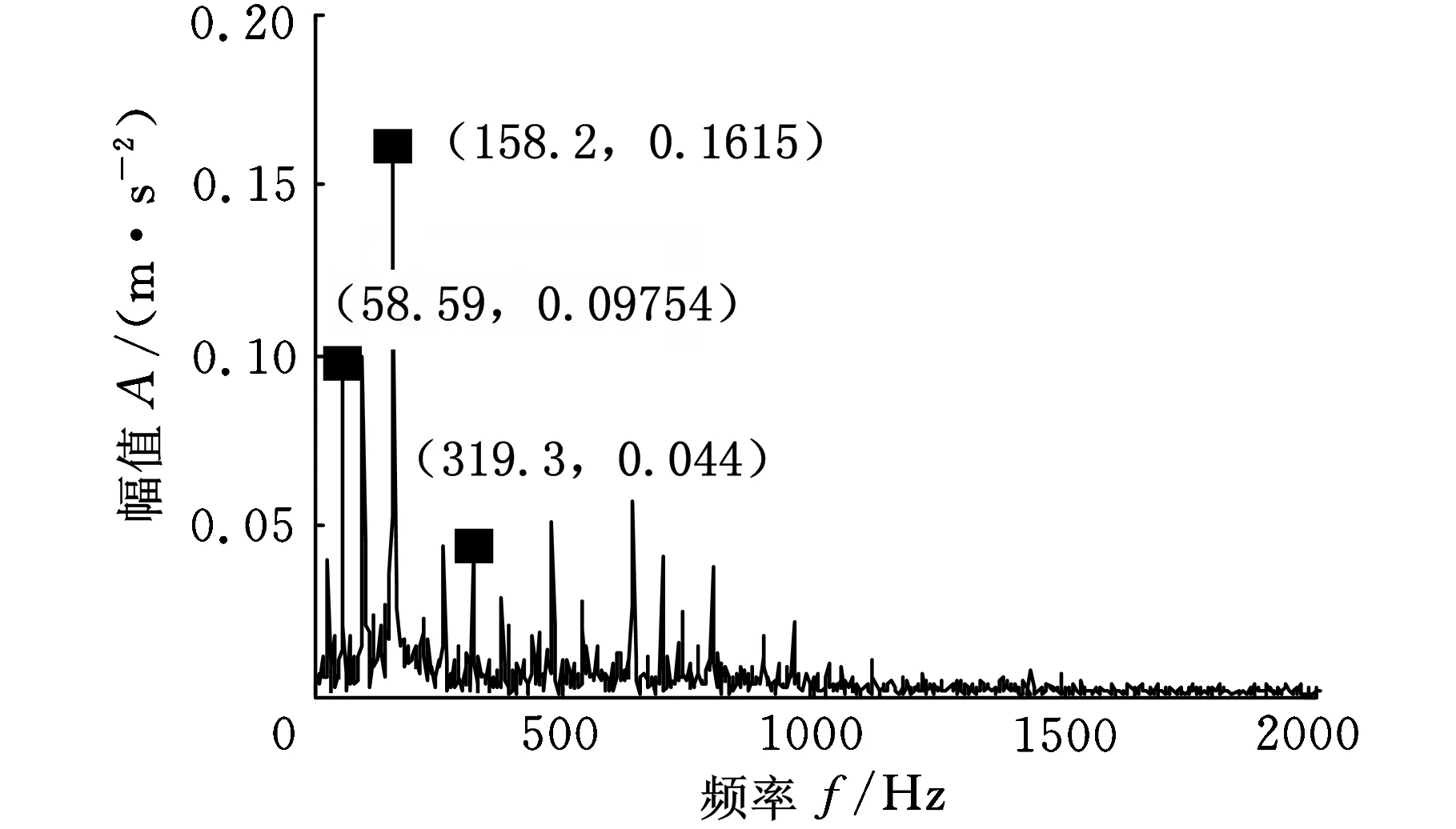
(a)IMF1分量的包络谱

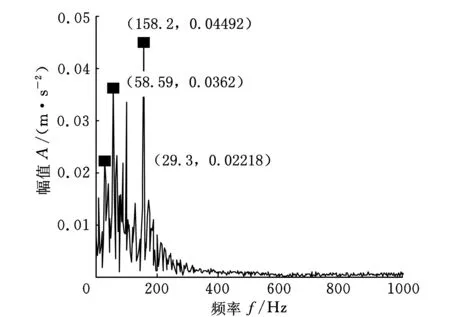
(b)IMF2分量的包络谱图10　采用能量算子解调得到的包络谱

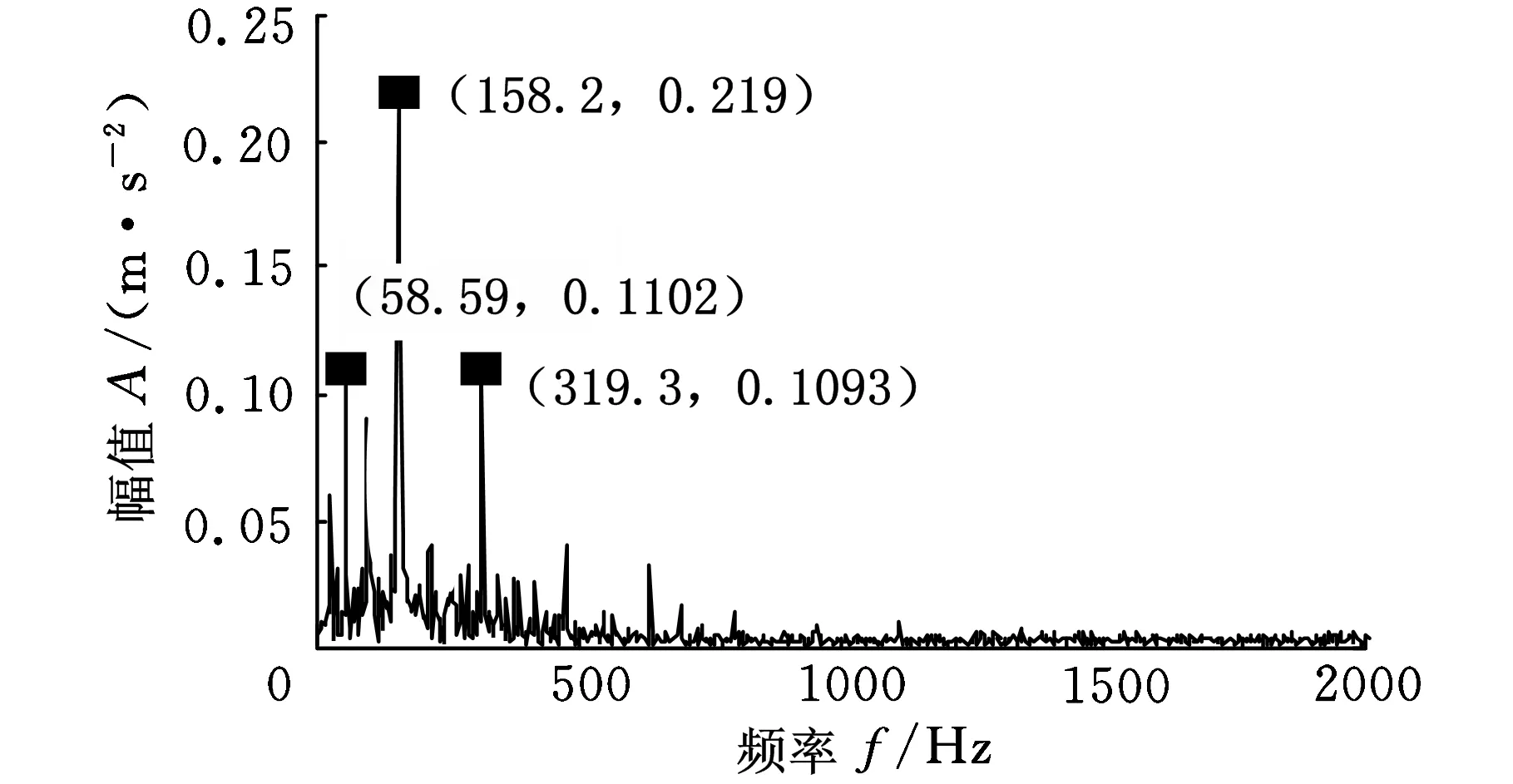
(a)IMF1分量的包络谱

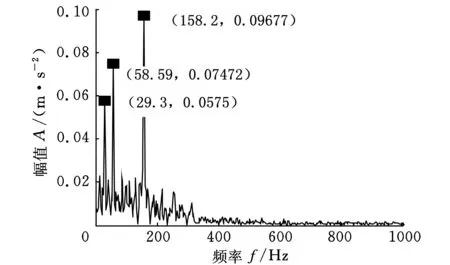
(b)IMF2分量的包络谱图11　采用对称差分能量算子解调得到的包络谱

从图10包络谱中可以看出，在29.3 Hz、58.59 Hz、158.2 Hz和319.3 Hz处出现了峰值，这和计算得到的转轴基频(29.16 Hz)、转轴基频的二倍频(58.32 Hz)、内圈故障的频率(157.94 Hz)及其二倍频(315.88 Hz)的值接近，都在误差允许范围内，但同时也可以看出，图10中存在着虚假干扰频率，并且这些频率的幅值比较大。对分解后前两个IMF分量进行对称差分能量算子解调，进而得到图11所示的包络谱，与图10相比，不仅在计算所得到的转轴基频的二倍频(58.32 Hz)、内圈故障的频率(157.94 Hz)及其二倍频(315.88 Hz)附近出现了峰值，而且峰值频率得到突出，几乎没有虚假干扰频率，其中只有几个幅值相当小的干扰频率，完全不影响故障诊断结果，故障特征更加明显直观。结合图8原始故障信号的包络谱可以看出，采用能量算子解调和对称差分能量算子解调提取出来的特征频率更加接近真实的故障频率，且采用对称差分能量算子解调得到包络幅值在特征频率29.3 Hz、58.59 Hz、158.2 Hz和319.3 Hz处比能量算子解调大，幅值比重增大，更有利于机械故障特征的提取，从而可以明确地判断轴承内圈产生了故障。

可见，将DEMD与对称差分能量算子解调相结合可以较好地完成对于轴承振动信号的处理和故障特征提取，效果优于基于DEMD的能量算子解调方法。

5　结论

(1)针对滚动轴承振动信号的非平稳特性和其周期性冲击特点，提出了基于DEMD和对称差分能量算子解调的滚动轴承故障诊断方法。

(2)该方法采用DEMD方法对故障轴承振动信号进行分解，从而将复杂的多分量信号分解成多个IMF分量，再对包含主要故障信息的IMF分量进行对称差分能量算子解调来提取信号的瞬时幅值和瞬时频率，进一步进行频谱分析，提取出特征频率，并与基于DEMD能量算子解调方法进行比较。对称差分能量算子解调具有解调精度高等特点，其性能要优于常用的Hilbert变换解调和能量算子解调方法。

(3)数值仿真和试验诊断实例的结果表明，基于DEMD和对称差分能量算子解调方法，能够更加准确地提取出振动信号的特征频率，实现轴承故障有效诊断。

[1]何正嘉, 陈进, 王太勇, 等. 机械故障诊断理论及应用[M].北京:高等教育出版社,2010.

[2]Huang N E，Shen Z，Long S R. A New View of Nonlinear Water Waves: the Hilbert Spectrum[J].Annual Review of Fluid Mechanics，1999，31：417-457.

[3]何旭.经验模式分解的研究及其在故障诊断中的应用[D]. 上海：上海交通大学, 2004.

[4]张文义，于德介，陈向民. 基于信号共振稀疏分解与能量算子解调的轴承故障诊断方法[J].中国电机工程学报， 2013，33(20)：111-118.

Zhang Wenyi, Yu Dejie, Chen Xiangmin. Fault Diagnosis of Rolling Bearings Based on Resonance-based Sparse Signal Decomposition and Energy Operator Demodulating[J]. Proceedings of the CSEE, 2013,33(20):111-118.

[5]任达千，杨世锡，吴昭同，等. 信号瞬时频率直接计算法与Hilbert变换Teager能量法比较[J].机械工程学报，2013，49(9)：42-48.

Ren Daqian, Yang Shixi, Wu Zhaotong, et al. Comparison of Instantaneous Frequency Directed Computing Method and Hilbert Transform and Teager Energy Method[J]. Journal of Mechanical Engineering, 2013, 49(9):42-48.

[6]Maragos P，Kaiser J F，Quatieri T F. Energy Separation in Signal Modulations with Application to Speech Analysis[J]. IEEE Transactions on Signal Processing，1993，41(10)：3024-3051.

[7]武和雷，朱善安，林瑞仲，等.基于能量算子解调法的滚动轴承故障诊断[J].农业机械学报，2003，38(1)：119-120.

Wu Helei, Zhu Shanan, Lin Ruizhong, et al. Fault Diagnosis of Rolling Bearing Based on the Energy Operator Demodulation Approach[J]. Transactions of the Chinese Society of Agricultural Machinery, 2003,38(1):119-120.

[8]胥永刚，陆明，谢志聪. 基于固有时间尺度分解的能量算子解调法及故障诊断应用[J].海军工程大学学报，2013，25(1)：27-31.

Xu Yonggang, Lu Ming, Xie Zhicong. Teager Energy Operator Demodulation Method Based on ITD and Its Applications in Fault Diagnosis[J].Journal of Naval University of Engineering, 2013,25(1):27-31.

[9]樊新海，何嘉武，王战军，等.基于 Teager能量算子的解调方法[J].装甲兵工程学院报，2009，23(4)：61-63.

Fan Xinhai, He Jiawu, Wang Zhanjun, et al. Demodulation Approach Based on Teager Energy Operator[J].Journal of Academy of Armored Force Engineering, 2009,23(4):61-63.

[10]鞠萍华，秦树人，赵金. 基于LMD的能量算子解调及其在故障特征信号提取中的应用[J]. 振动与冲击，2011，30(2)：1-4.

Ju Pinghua, Qin Shuren, Zhao Jin.Energy Operator Demodulating Approach Based on LMD and Its Application in Extracting Characteristics of a Fault Signal[J]. Journal of Vibration and Shock, 2011,30(2):1-4.

[11]李蓉，于德介，陈向民. 基于形态分量分析与能量算子解调的齿轮箱复合故障诊断方法[J].中国机械工程，2013，24(13)：1789-1795.

Li Rong, Yu Dejie, Chen Xiangmin. A Compound Fault Diagnosis Method for Gearbox Based on Morphological Component Analysis and Energy Operator Demodulating[J].China Mechanical Engineering, 2013,24(13):1789-1795.

[12]景蓓蓓，李鸿光. 基于微分的经验模式方法在转子裂纹和碰摩故障诊断中的应用[J]. 噪声与振动控制，2009，5(1)：66-69.

Jing Beibei, Li Hongguang. Fault Diagnoses of Cracked Rotor and Rub-impact Rotor Based on DEMD Method[J].Noise and Vibration Control, 2009,5(1):66-69.

[13]王冰，李洪儒，许葆华. 基于LMD和平滑Teager能量算子解调的电机滚动轴承故障特征提取[J].机械传动，2012，36(9)：89-92.

Wang Bing, Li Hongru, Xu Baohua.Fault Feature Extraction of Motor Rolling Bearing Based on LMD and Smoothed Teager Energy Operator Demodulating[J].Journal of Mechanical Transmission, 2012,36(9):89-92.

[14]高云鹏，李峰，陈婧，等. 改进能量算子Nuttall窗频谱校正的闪变测量方法[J]. 仪器仪表学报，2014，35(4)：745-753.

Gao Yunpeng, Li Feng, Chen Jing, et al. Voltage Flicker Measurement Method Using Improved Teager-Kaiser Energy Operator Based on Nuttall Window Spectral Correction[J]. Chinese Journal of Scientific Instrument, 2014, 35(4):745-753.

[15]黄椒治，林慧斌，丁康. 基于广义解调平滑能量分离算法的瞬时频率估计[J]. 振动工程学报，2014，27(2)：281-288.

Huang Jiaozhi, Lin Huibin, Ding Kang. Instantaneous Frequency Estimation Based on Generalized Demodulation Smoothed Energy Separation Algorithm[J].Journal of Vibration Engineering, 2014,27(2):281-288.

(编辑袁兴玲)

Fault Diagnosis of Rolling Bearings Based on DEMD and Symmetric Difference Energy Operator Demodulation

Meng ZongJi Yan

Key Laboratory of Measurement Technology and Instrumentation of Hebei Province,Yanshan University,Qinhuangdao,Hebei，066004

Aimed at the modulated characteristics of the mechanical fault vibration signals, in order to extract amplitude and frequency informations of multi-component amplitude modulation and frequency modulation signals, a method was put forward based on the DEMD combining with symmetric difference energy operator demodulation. First of all, the original vibration signals were decomposed by DEMD algorithm, getting a number of single component signal, and then symmetric difference of three energy operator demodulation was used for every single component signal, getting instantaneous amplitude and instantaneous frequency of each single component signal, and the spectral envelope was calculated, finally the method was applied to the simulation signals and the rolling bearing fault signals. The experimental results show that the method can accurately extract the fault features of mechanical fault signals and realize rotating machinery fault diagnosis effectively.

differential-based empirical mode decomposition(DEMD); symmetric difference energy operator; rolling bearing; fault diagnosis

2014-07-24

国家自然科学基金资助项目(51105323)；河北省自然科学基金资助项目(E2015203356)；河北省高等学校科学研究计划资助重点项目(ZD2015049)

TN911.6;TH133.3DOI：10.3969/j.issn.1004-132X.2015.12.017

孟宗，男，1977年生。燕山大学河北省测试计量技术及仪器重点实验室教授、博士。主要研究方向为机械设备监测与故障诊断、动力学建模、信号检测与处理等。季艳，女，1987年生。燕山大学河北省测试计量技术及仪器重点实验室硕士研究生。