无理论刃形误差直齿插齿刀设计

李　佳　李晓群　王　鹏　邹　钰

天津大学机构理论与装备设计教育部重点实验室,天津,300072

无理论刃形误差直齿插齿刀设计

李佳李晓群王鹏邹钰

天津大学机构理论与装备设计教育部重点实验室,天津,300072

为了提高插齿加工精度，提出一种无理论刃形误差插齿刀具设计方法。基于曲面共轭原理，根据待加工齿面和插齿加工运动特点,建立齿面共轭面的数学模型。前刀面选择球面形式，应用割线法求得共轭面和前刀面的交线，进而建立切削刃的数学模型。从刀具重新刃磨后仍能满足无理论刃形误差要求的角度出发，求取多条切削刃，利用所求得切削刃曲线构造后刀面，建立后刀面数学模型。插齿加工实验表明，采用无理论刃形误差直齿插齿刀加工工件，刀具重磨前后加工精度有较好的一致性,从而证明了该设计方法的正确性和可行性。

插齿加工；插齿刀设计；刃形误差； 渐开线

0　引言

插齿加工是常用的渐开线齿轮粗加工技术之一。众所周知,影响插齿加工精度的主要因素是机床精度、刀具精度和夹具精度。目前，数控插齿机床和夹具的设计制造精度已经能够满足齿轮半精加工的需求。如果能够提高插齿刀具设计制造精度，使之与插床和夹具精度相匹配，就有望使插齿加工精度进一步得到提高，这对于齿轮制造行业的发展具有重要意义。

在直齿插齿刀设计方面,基于渐开线齿轮变位原理的插齿刀设计方法在设计原理上存在齿形误差。为了实现工艺目标，常采用齿廓修形的技术方法进行处理。文献[1]基于直齿插齿刀切削刃投影与理论渐开线在分度圆处相切的原理,推导出了齿形角的修正公式,但是在渐开线两端仍有较大的偏差。王化培[2]提出一种插齿刀齿形角的修正方法，使切削刃投影圆处于齿顶圆和基圆之间与理论渐开线相切，计算实例验证了其修正效果。但该方法的不足之处在于插齿刀渐开螺旋面分度圆压力角不为20°。文献[3]提出一种基于齿廓倾斜偏差误差补偿的优化迭代算法来进一步减小插齿刀齿廓偏差。相比之下，该方法对小模数齿轮更为有效。其他相关研究[4-8]也是通过齿形修正或优化的方法来减小直齿插齿刀的齿形误差。这些方法在一定程度上提高了刀具齿形精度，但不可能从根本上消除理论设计误差。

除了无法避免理论齿形误差这一弊端之外，直齿插齿刀还存在重磨前后精度一致性差的弊端。随着重磨次数的增加,插齿刀齿形误差呈现由大变小再变大的变化趋势,显然，这会影响插齿刀可重磨次数和寿命。文献[9]基于MATLAB遗传算法工具箱,以刀具寿命为目标函数,对插齿刀参数进行优化,使刀具的可重磨厚度与传统优化方法相比增加了48.98%,但是该研究也未能根本解决重磨前后齿形误差不一致的问题。

针对目前直齿插齿刀存在齿形误差以及重磨之后精度一致性差的问题，本文提出一种基于曲面共轭原理[10-11]的无理论刃形误差直齿插齿刀设计方法。

1　刀具设计原理

直齿插齿刀结构如图1所示，其每个刀齿由前刀面、侧刃、侧后刀面、顶刃和顶后刀面五部分组成。实际加工中，侧刃决定着齿形加工精度，而后刀面又决定着侧刃形状和精度，因此本文重点研究侧刃及侧后刀面设计原理和方法。

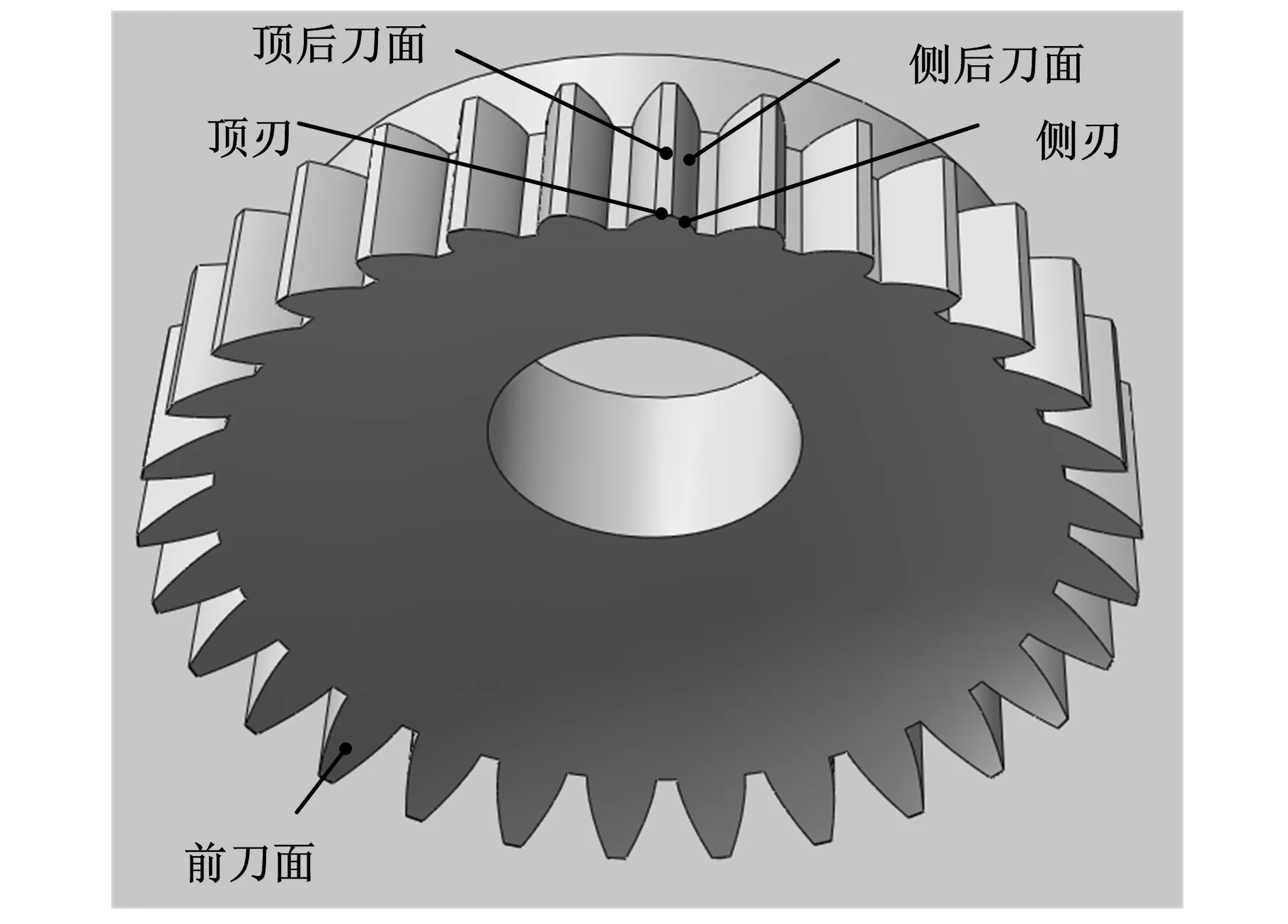
图1　直齿插齿刀结构

现行直齿插齿刀设计是以两个齿轮啮合为基础的,为了叙述方便,将这两个齿轮分别称为工件轮和刀具轮。在刀具轮未形成前角、后角之前,刀刃是标准渐开线,不会出现理论误差。但是为了构造后角，侧后刀面设计成渐开螺旋面;为了构造前角,前刀面设计成圆锥面。这样刀刃就成为一条空间曲线,而非标准渐开线。文献[12]在研究直齿剐齿刀设计理论中,提出了一种无理论刃形误差的设计方法,通过前刀面直接与刀具轮齿面求交形成切削刃。这种切削刃由于处在刀具轮上,因此刃形设计不存在理论误差。然而通过刀具轮设计插齿刀具有很大的局限性,首先是后刀面构造灵活性较差，不利于刀具参数优化;其次是设计方法通用性较差，不适用于其他非渐开线齿形插齿刀设计。注意到工件轮齿面与刀具轮齿面相互啮合的实质是曲面共轭运动，因此本文直接从曲面共轭原理出发,抛开刀具轮的限制,提出无理论刃形误差直齿插齿刀设计方法。

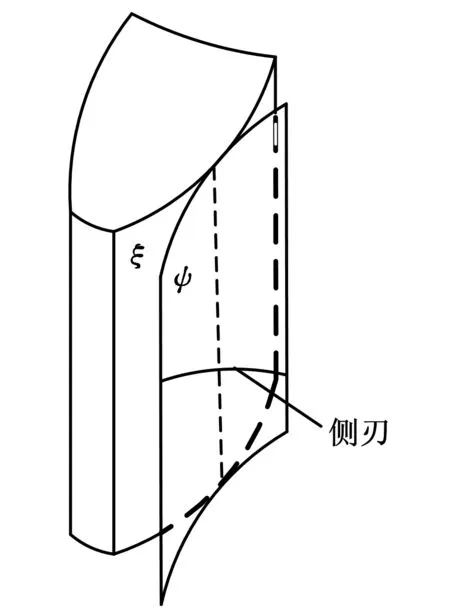
图2　设计原理

如图2所示,根据工件参数建立待加工齿面ξ的数学模型,按照插齿加工运动模型求得ξ的共轭面ψ,构造适当的前刀面,与共轭面求交得到切削刃。这样得到的切削刃一定处于待加工齿面的共轭面上,因此不存在刃形误差。刀具重磨之后，会产生新的前刀面,其形状也要发生相应变化,同时也会有新的共轭面与之相对应，两者再次求交获得新的切削刃。按照上述方法可以获得多条切削刃,利用这些切削刃曲线构造后刀面，可保证每次重磨之后切削刃仍处在共轭面上，刃形精度有很好的一致性。

2　共轭面求取

根据曲面共轭原理,已知曲面与其共轭面是机构中两构件上用以实现给定运动规律连续相切的一对曲面。因此，为了求取待加工齿面的共轭面,建立工件齿面的数学模型，以及每一时刻共轭接触点的相对运动速度模型，进而求取共轭面。

2.1工件齿面

如图3所示,在工件坐标系S1(z1轴与工件轴线重合,O1x1y1平面与工件上端面重合,x1轴与工件某一齿的对称线重合)中,齿形渐开线的极坐标方程为

(1)

图3　工件坐标系与工件齿面

可得齿面的数学模型：

(2)

φK=s/r-2(θK-θ)

(3)

式中,rb为基圆半径;rK为渐开线齿廓上某点K对应的圆半径;θK为K点处的展角；αK为K点处的压力角;h为齿面上某点M到上端面的距离;φK为K点对应中心角的一半;s、r分别为分度圆齿厚和半径;θ为分度圆处的展角。

进而可得齿面上某一点处的法矢N1:

(4)

2.2相对运动速度

插齿加工过程中的运动主要包括插齿刀上下往复运动和分齿展成运动。为了计算共轭接触点的相对运动速度,基于插齿加工运动特点,在图3所示工件坐标系基础上,建立如图4所示的坐标系。Sp、S0是固定坐标系,分别对应工件坐标系S1和刀具坐标系S2的初始位置。xp轴与x0轴重合;zp轴与z0轴平行,且两者之间的距离为工件与刀具的中心距a。在某一时刻,S1、S2分别绕zp轴和z0轴旋转φ1和φ2角度。同时,刀具坐标系S2沿z0轴负方向直线运动l长度。

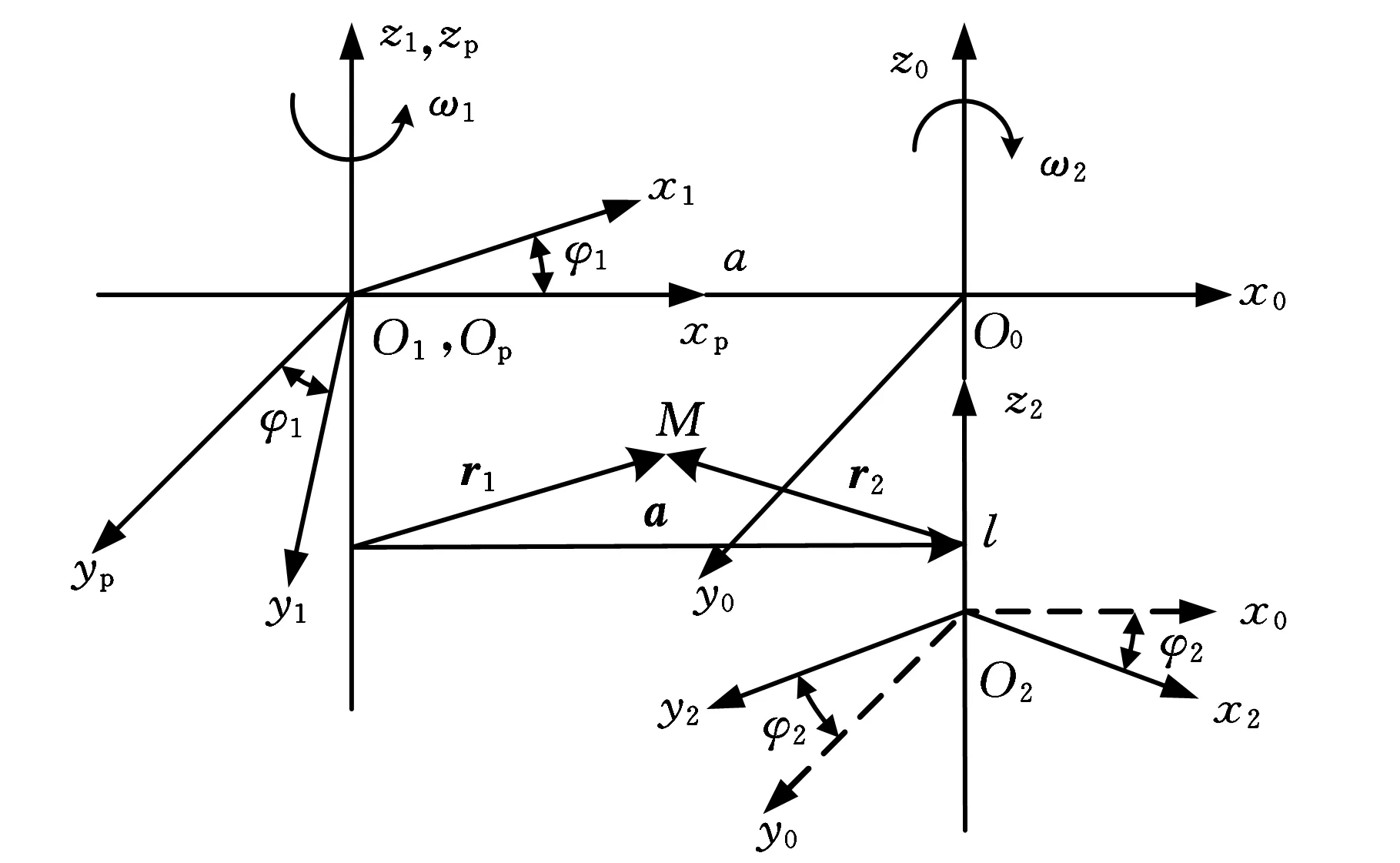
图4　设计计算坐标系

加工中,转角φ1和φ2满足：

(5)

式中，ω1、ω2分别为工件和刀具绕自身轴线旋转的角速度。

在坐标系S0中计算相对运动速度,设接触点M在S0中的坐标为(x,y,z),刀具上接触点相对于工件上接触点的运动速度为

v21=ω2×r2-ω1×r1+v2

(6)

式中,ω1、ω2分别为工件和刀具角速度矢量;v2为刀具直线运动速度矢量；r1、r2分别为工件和刀具旋转运动向径。

设S0坐标系x0轴、y0轴、z0轴的单位矢量分别为i、j、k;Sp坐标系xp轴、yp轴、zp轴的单位矢量分别为ip、jp、kp,则有:

r2=xi+yj

(7)

r1-r2=a=ai

(8)

ω1=ω1kp

(9)

ω2=-ω2k

(10)

v2=-vk

(11)

式中,v为插齿刀上下往复直线运动的速度大小。

根据S0、Sp坐标系的相对位置关系有：

kp=k

(12)

将式(5)、式(7)～式(12)代入式(6),可得相对运动速度矢量为

v21=vxi+vyj+vzk

(13)

vx=ω2y+ω1y

vy=-ω2x-ω1(a+x)

vz=-v

2.3共轭面求取

如果两个面共轭,它们在接触点处的相对运动速度应该位于该处的公切面内,即满足：

N·v21=0

(14)

在同一坐标系下考察这一关系,式(13)已得到S0坐标系下相对运动速度v21,式(4)已得到在工件坐标系S1中表示的齿面的法矢,因此需要将齿面的法矢从S1坐标系变换到S0坐标系。由图4可得S1坐标系到S0坐标系的矢量变换矩阵:

(15)

进而可求得S0坐标系中工件齿面的法矢为

(16)

同时,M点在S0中的坐标可由S1中坐标变换得到：

(17)

式中，M01为S1到S0的坐标变换矩阵。

联立式(2)、式(4)、式(13)～式(17)可以解得对应于齿面每一点的φ1值。将接触点坐标由S1坐标系变换到S2坐标系:

(18)

式中,M21为S1到S2的坐标变换矩阵。

按照以上方法,可以求得共轭面上任一点的坐标,即求得了整个共轭面,简化表示为

(19)

3　前刀面设计

现有插齿刀的前刀面一般为圆锥面。文献[13]比较了圆锥面和球面,指出当顶刃处具有相同的前角时,采用球面形式的前刀面刀具强度高,工艺性也较好,因此球面更适合作为刀具前刀面。参考该研究成果,本文亦采用球面形式的前刀面。

如图5所示,设未重磨前初始前刀面的球面半径为R0,齿顶圆半径为ra0。重磨之后,前刀面球心位置和球面半径发生变化;设重磨前后前刀面沿z2轴方向的距离为Δb,此时齿顶圆半径为ra,球面半径为R,球心到前端面的距离为R1。根据图5所示几何关系,可得：

ra=ra0-Δbtanγz

(20)

图5　刀具与刀具坐标系

进而得：

(21)

(22)

式中,αz、γz分别为插齿刀顶刃前角和顶刃后角。

设球面上一点在O2x2y2平面的投影到坐标原点的连线与x2轴的夹角为φ;该点到球心的连线与z2轴的夹角为θ,可得前刀面参数表达式：

(23)

4　侧刃求取

按照前述刀具设计原理,侧刃为齿面的共轭面与前刀面的交线,因此侧刃上的点满足:

(24)

由于共轭面对各个参数的偏导数不便于求解,本文采用割线法[14]求解非线性方程组式(24)。

该方程组总共含有4个未知参数,方程数小于未知数个数,因此需要假定一个参数已知。因为参数h的范围是工件的齿宽,便于确定,因此可以将h在此范围内均匀离散后代入式(24),然后求其他三个未知参数。

割线法的迭代格式为

x(t+1)=x(t)-(J(x(t),h(t)))-1F(x(t))

x=(rK,θ,φ)T

F(x(t))=(f1,f2,f3)

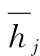
(25)

i,j=1,2,3

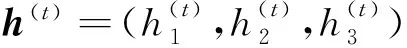
(26)

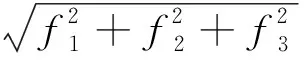
计算出参数初始值后,按如下过程迭代:

(1)给定计算误差控制量ζ和迭代步长系数hj,并令x(0)=(rK0,θ0,φ0)T,t=0。

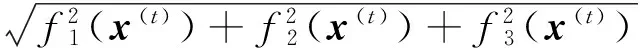
(27)

由以上迭代方法,可以求出侧刃上任一点坐标。

5　侧后刀面设计

侧后刀面的形成过程如图6所示,首先按照上述方法计算齿面的共轭面c1,继而与前刀面q1求交获得曲线r1(即切削刃)。为了构造刀具后角,减小刀具齿顶圆半径,同时减小工件与刀具之间的中心距a,再次计算获得齿面的共轭面c2,此时对应的前刀面为q2,两者再次求交获得曲线r2。按照上述方法，依次求得曲线r3,r4，…，由这些曲线构造侧后刀面。

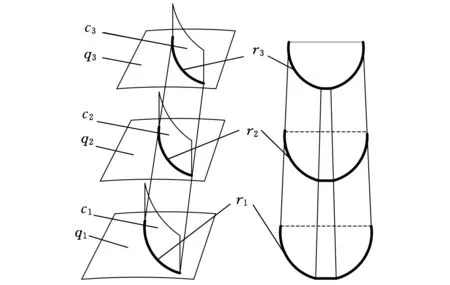
图6　侧后刀面设计

设重磨前后中心距的变化量为Δa,由图5可得：

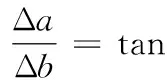
(28)

由上述侧后刀面的形成过程可知,侧后刀面是若干切削刃的集合。理论上由Δa和式(27)可以求得侧后刀面上所有点。考虑到工程实践的可行性,由侧后刀面上的若干个点作为型值点,采用三次B样条曲面对侧后刀面进行拟合。在进行刀具设计时，根据精度要求，确定型值点的个数。在刀具的可重磨范围内,侧后刀面由M条均匀分布的切削刃构成；由式(27)在每条切削刃上计算出N个点的坐标,则得到侧后刀面上M×N个型值点。由这些型值点，可以构造侧后刀面的数学模型：

(29)

其中,N1,3(u)、Nj,3(w)为三次B样条基函数;Pi,j为由型值点得到的控制点。

按照上述方法,可以完成无理论刃形误差插齿刀前刀面、侧刃和侧后刀面的设计,其顶刃和顶后刀面设计方法与现有方法类似,本文不作赘述。

6　加工实例

为了验证无理论刃形误差插齿刀设计理论的正确性,笔者进行了加工精度一致性实验。

所要加工的直齿圆柱齿轮参数如表1所示,按照2.1节内容建立工件齿面的数学模型，求得工件齿面的法矢。依据表2所示的刀具参数和加工参数(中心距的初始值a0定为93.126 mm),按照前述计算过程可求得插齿刀的初始切削刃上点的坐标。取每次重磨中心距的变化量Δa=0.1 mm,此时中心距a=a0+Δa,进而由第2节计算过程求取共轭面。由式(28)可计算Δb,进而由第3节的计算过程求得前刀面。按照第4节的计算过程求得重磨之后侧刃上点的坐标。中心距再次变化，重复以上过程，求得下一次重磨之后侧刃上点的坐标。本实验设计的后刀面由初始切削刃以及4次重磨之后形成的4条侧刃构成。每条侧刃上求取8个点，总共获得40个型值点坐标，由这些型值点构造三次B样条曲面作为刀具后刀面。

表1　工件参数

表2　刀具参数和加工参数

通过计算获得的侧后刀面上部分型值点的坐标如表3所示。

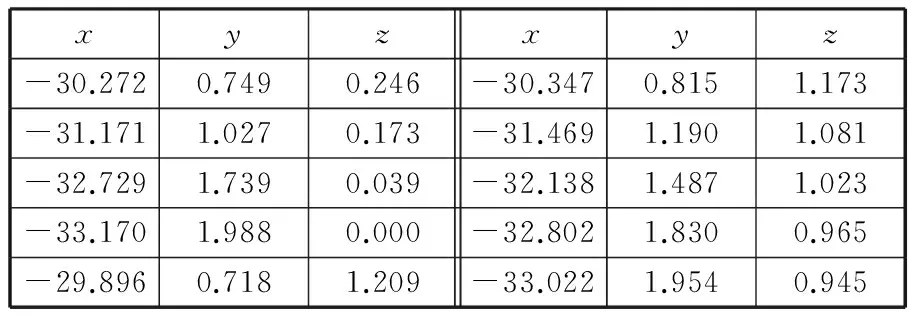
表3　侧后刀面上部分点的坐标　mm

图7　插齿刀制造图8　工件加工

图9　重磨之后的插齿刀图10　齿轮测量仪

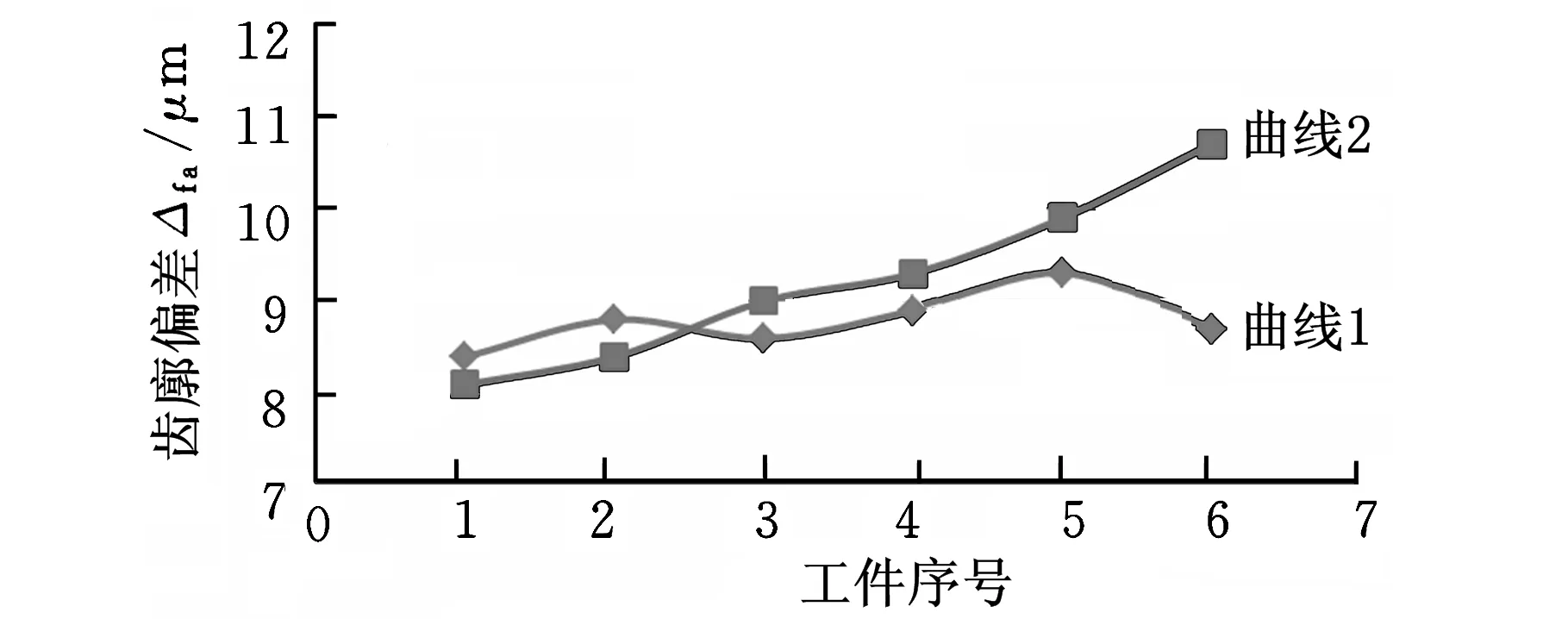
图11　实验工件的齿廓偏差

插齿刀终加工在图7所示的五轴工具磨床上完成；试件插齿加工在YKS5120插齿机床上完成,如图8所示。为了验证重磨前后插齿刀加工精度的一致性，本文进行了分组插齿加工实验。实验分为三组，分别采用重磨之前、重磨一次、重磨两次的插齿刀，每组各加工两个工件，重磨之后的刀具如图9所示。在L100齿轮测量仪上检测齿轮齿形加工精度,如图10所示。其中，齿面的齿廓偏差Δfa变化范围在1.6 μm以内(如图11中曲线1所示),表现出很好的精度一致性。在相同的条件下用传统插齿刀进行重磨加工精度一致性实验。实验同样重磨两次共三组,每组加工两个工件，每次刃磨量与新型插齿刀重磨实验的刃磨量相同。在齿轮测量仪上检测齿轮齿形精度，获得齿廓偏差的变化情况如图11曲线2所示，可以看到前两个工件精度较好，随着刀具的不断重磨，刀具齿形误差不断增大，齿轮加工精度不断降低，齿廓偏差的最大变化量为2.6 μm。通过加工精度一致性的对比实验，证明了新型插齿刀有较大的优越性。

7　结论

(1)针对传统插齿刀存在齿形误差的问题,基于曲面共轭原理,提出了一种无理论刃形误差的插齿刀设计方法。以渐开线齿轮直齿插齿刀为例,给出了刀具设计过程。

(2)所提出的侧后刀面的构造方法可保证刀具重刃磨前后刀刃均不存在理论误差,从而保证加工精度的一致性，明显提高了插齿加工零件的质量。

(3)重磨前后加工精度一致性实验表明，无理论刃形误差插齿刀设计方法是正确可行的。在重磨之后加工精度一致性方面本文方法明显优于传统插齿刀。

(4)在相同的加工条件下,采用无理论刃形误差插齿刀加工零件，精度应该明显得到提高。受现有工具磨床和插齿机床精度限制，本文未能进行插齿精度的对比实验,这个结论有待进一步的工作加以证实。

(5)本文给出的设计方法可推广应用于非渐开线插齿刀设计。

[1]袁哲俊，刘华明，唐宜胜.齿轮刀具设计[M].北京:新时代出版社,1983.

[2]王化培.直齿外啮合渐开线插齿刀齿形误差及修正新法[J].四川兵工学报,1998,19(4):21-23.

Wang Huapei.The Tooth Profile Error and New Revised Method of Straight Tooth Outside Meshing Involute Shaping Cutter[J].Journal of Sichuan Ordnance,1998,19(4):21-23.

[3]凌四营, 宋润州, 王庆男, 等. 插齿刀齿形角修正算法与精度探讨[J]. 机械设计与制造,2011(1):164-166. Ling Siying, Sun Runzhou, Wang Qingnan,et al. The Tooth Profile Angle Correction Algorithm and Precision Study of Gear Shaping Cutter[J]. Machinery Design & Manufacture, 2011(1):164-166.

[4]Huang Chin-Lung,Fong Zhang-Hua,Chen Shi-Duang. Profile Correction of a Helical Gear Shaping Cutter Using the Lengthwise-reciprocating Grinding Method[J].Mechanism and Machine Theory,2009,44(2):401-411.

[5]Li Biwen,Xiao Jinfeng,Zhang Chunliang.Prediction and Control for Profile Angle Error of Slotting Cutter of Herringbone Gear in Turbine Redactor[J].Advanced Materials Research,2011,139/141:1864-1868.

[6]Radzevich S P.Diagonal Shaving of an Involute Pinion:Optimization of the Geometric and Kinematic Parameters for the Pinion Finishing Operation[J].International Journal of Advanced Manufacturing Technology,2007,32(11/12):1170-1187.

[7]李佩芝.负前角硬质合金插齿刀的齿形误差与齿形角修正[J].工具技术,1999(3):21-22.

Li Peizhi.The Tooth Profile Error and Tooth Profile Angle Correction of Negative Rake Angle Carbide Gear Shaping Cutter[J].Tool Engineering,1999(3):21-22.

[8]马霄,王伟.提高直齿插齿刀构形精度的刃磨工艺方案研究[J].工具技术,2008,42(12):47-50.

Ma Xiao,Wang Wei.The Grinding Process Research of Improving the Spur Gear Shaper Cutter Configuration Precision[J].Tool Engineering,2008,42(12):47-50.

[9]唐德威,刘丹,邓宗全,等.基于Matlab遗传算法工具箱的内插齿刀优化设计[J].机械制造,2012,50(11):22-25.

Tang Dewei,Liu Dan,Deng Zongquan,et al.The Optimization Design of Inner Gear Shaper Cutter Based on Matlab Genetic Algorithm Toolbox[J].Machinery Manufacturing,2012,50(11):22-25.

[10]高业田,李华敏,徐晓俊.双自由度共轭曲面啮合理论 [J].哈尔滨工业大学学报,1989(4):66-76.

Gao Yetian,Li Huamin,Xu Xiaojun.The Meshing Theory of Double Freedom Degree Conjugate Curved Surface[J].Journal of HarbinInstitute of Technology University,1989(4):66-76.

[11]董黎君.共轭旋转曲面的理论分析及计算机绘制[J].太原工业大学学报,1997,28(2):13-16.

Dong Lijun.Theoretical Analysis and Computer Drawing of Conjugate Revolution Curved Surface[J].Journal of Taiyuan University of Technology,1997,28(2):13-16.

[12]Chen Xinchun,Li Jia,Lou Benchao.A Study on the Design of Error-free Spur Slice Cutter[J].International Journal of Advanced Manufacturing Technology,2013,68(1/4):727-738.

[13]陈新春,李佳,贺友平.直齿剐齿刀结构设计与计算[J].天津大学学报,2012,45(5):411-416.

Chen Xinchun,Li Jia,He Youping.Structure Design and Calculation of Spur Slice Cutter[J].Journal of Tianjin University,2012,45(5):411-416.

[14]邹健,宋述刚,陈忠.一个用割线法求解非线性方程组的异步并行算法[J].太原师范学院学报(自然科学版),2006,5(2):9-10.

Zou Jian,Song Shugang,Chen Zhong.An Asynchronous Parallel Algorithm Using the Secant Method to Solve Nonlinear Equations[J].Journal of Taiyuan Teachers College(Natural Science Edition),2006,5(2):9-10.

(编辑卢湘帆)

Design of Straight Teeth Gear Shaping Cutter without Theoretical Cutting Edge Profile Errors

Li JiaLi XiaoqunWang PengZou Yu

Key Laboratory of Mechanism and Equipment Design of Ministry of Education,Tianjin University,Tianjin,300072

Aiming at improving the gear shaping machining precision,a design method of a gear shaping cutter without theoretical cutting edge profile errors was proposed. Based on the conjugation theory of curved surface,a mathematical model of the conjugate surface of the tooth surface was built according to the tooth surface to be machined and the movement characteristics of gear shaping. The sphere surface was chosen as rake face, and the intersecting line of the conjugate surface and the rake face was get by secant method, and the mathematical model of the cutting edge was built. Many similar cutting edges were get from the point that the requirements of without theoretical cutting edge profile errors could be met after grinding.The flank face was formed by these cutting edges, and its mathematical model was built.The gear shaping experiments show that the machining precision has good consistency using the cutter before and after grinding , and the correctness and feasibility of this design method is confirmed.

gear shaping;shaping cutter design;cutting edge profile error;involute

2014-08-13

国家自然科学基金资助项目(51175376)

TH132.417DOI：10.3969/j.issn.1004-132X.2015.12.001

李佳,男,1955年生。天津大学机械工程学院教授。主要研究方向为数控装备、先进加工工艺。李晓群，男，1988年生。天津大学机械工程学院硕士研究生。王鹏,男,1990年生。天津大学机械工程学院博士研究生。邹钰，男，1990年生。天津大学机械工程学院硕士研究生。