多输出3D打印冗余并联机器人的设计与分析
2015-10-29常定勇方跃法
常定勇 方跃法
北京交通大学,北京,100044
多输出3D打印冗余并联机器人的设计与分析
常定勇方跃法
北京交通大学,北京,100044
设计了一种新型多输出3D打印机器人,该机器人机构以Delta并联机构为主构型,以Stewart并联机构为辅助构型,在末端执行器上布置多个打印头,实现多输出。根据建立的运动学模型,分析了该机器人机构的运动学反解,得到速度雅可比矩阵,解得各驱动关节的速度和加速度。给定动平台的运动轨迹,仿真分析了机构的运动协调性,并对机构的灵巧性与静刚度进行了分析。
3D打印机器人;并联机构;雅可比矩阵;灵巧性;静刚度
0 引言
打印材料和设备的不断创新和发展使得3D打印技术在电子产品、汽车、航空、医疗、地理信息及艺术设计等领域得到越来越广泛的应用[1-3]。由于3D打印高端RP系统价格昂贵, 运行成本高,对环境要求比较高,且需要专人操作和维护,而基于喷射技术的三维打印(3DP)成形技术设备和材料便宜,运行成本低,操作简单,成形过程无污染,打印速度快,且适合办公室环境,可制作精细复杂零件,故基于喷射技术的3D打印技术成为RP行业近几年的研究热点。1993年麻省理工学院(MIT)获3D实体印刷技术专利,为3D打印技术迅速发展提供了平台[1,4]。2005年Z Corp.公司成功研制了基于喷墨技术的高清彩色打印机Spectrum Z510[5],该公司的Z系列打印机是采用MIT发明的基于喷射黏结剂粉末工艺的3DP设备,其构型均为串联机构,相关研究人员对该3D打印机的打印精度进行了分析[6]。RepRap项目已经发布了4个版本的3D立体打印机,分别为:2007年3月发布的Darwin、2009年10月发布的Mendel、2010年发布的Prusa Mendel和Huxley,这些3D打印机是基于笛卡儿坐标的串联结构打印机[7]。美国Fab@home实验室于2009年研制出第一台具有两个打印头的串联结构开源双色3D打印机Model 2,这种打印机价格便宜、体积小,适合家庭桌面办公[8-9]。最近几年,国内外出现了采用聚乳酸(Polylacitc Acid)材料打印实体模型的并联机构3D打印机,如3D打印Delta机器人[10]等,能够满足一般性产品的打印要求。
现有的大部分3D打印机只有一个打印头一个输出,一台打印机只能生产制造一个产品,不能同时打印多个产品,打印批量产品耗费时间长、生产成本高。本文设计一种新型基于喷射技术的3DP成形技术多输出3D打印并联机器人,其结构以Delta并联机构为主构型,为了确保打印机末端执行器的刚度和运动的精度,通过3组对称分布的平行双联滚珠丝杠副将每根刚性连接杆与定平台连接,构成Stewart并联机构,为动平台提供支撑力,并且通过控制动平台运动时产生的振动提高打印机末端执行器的运动平稳性。
1 机构的结构描述
设计的多输出3D打印并联机器人样机模型如图1所示。由定平台1、动平台11、3条由滚珠丝杆副7和杆端关节轴承从动杆4组成的运动支链、驱动电机和联轴器8构成Delta并联机构(主体机构);由3根刚性连杆10、6条由3组双联滚珠丝杆副3和球副5以及连杆组成的运动支链、驱动电机2构成Stewart并联机构(辅助机构);设置有4个打印头6、4个工作台9。结合以上各部分,整体构成一个闭环系统。
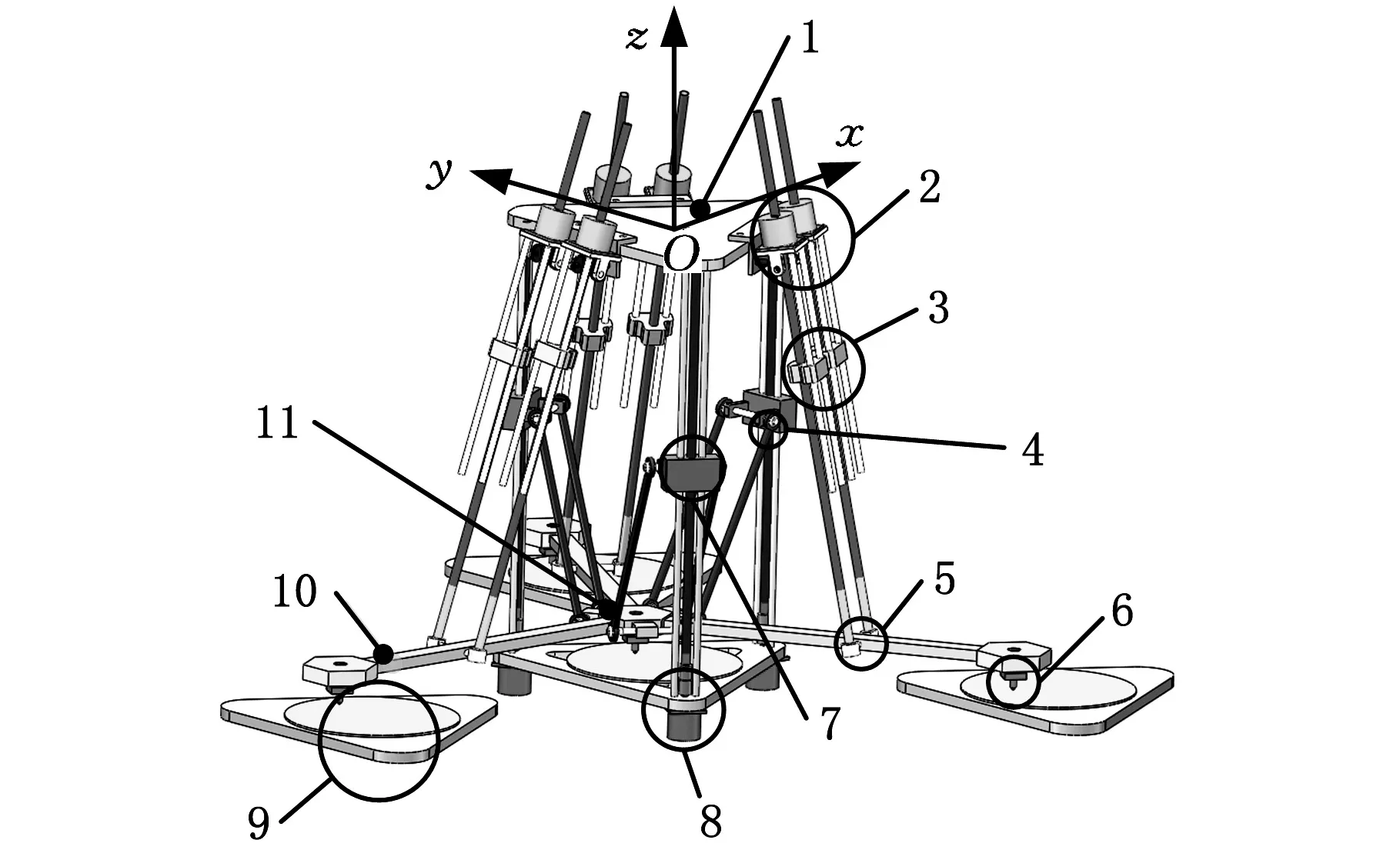
1.定平台 2.驱动电机 3.双联滚珠丝杆副 4.从动杆5.球副 6.打印头 7.滚珠丝杆副 8.联轴器9.工作台 10.刚性连杆 11.动平台图1 多输出3D打印并联机器人样机模型
为了简化机构模型,提取图1中机构的一条支链进行具体表达,见图2。ΔA1A2A3与ΔB1B2B3为等边三角形,固定坐标系Oxyz与动态坐标系O1x1y1z1的原点分别为定平台和动平台的几何中心,x轴(x1轴)与OA1(O1B1)共线,y轴(y1轴)平行于边A2A3(B2B3), z轴(z1轴)垂直向上,定平台与动平台的外接圆半径分别为R和r,即|OA1|=|OA2|=|OA3|=R,|O1B1|=|O1B2|=|O1B3|=r,并且R>r。O1Q3过点N3,|O1Q3|=d>R。设计时每组对应的平行双联滚珠丝杆副采用同步驱动,在运动过程中,两根驱动丝杆始终保持平行,限制辅助机构3个转动自由度,该机器人机构只有3个纯移动自由度。
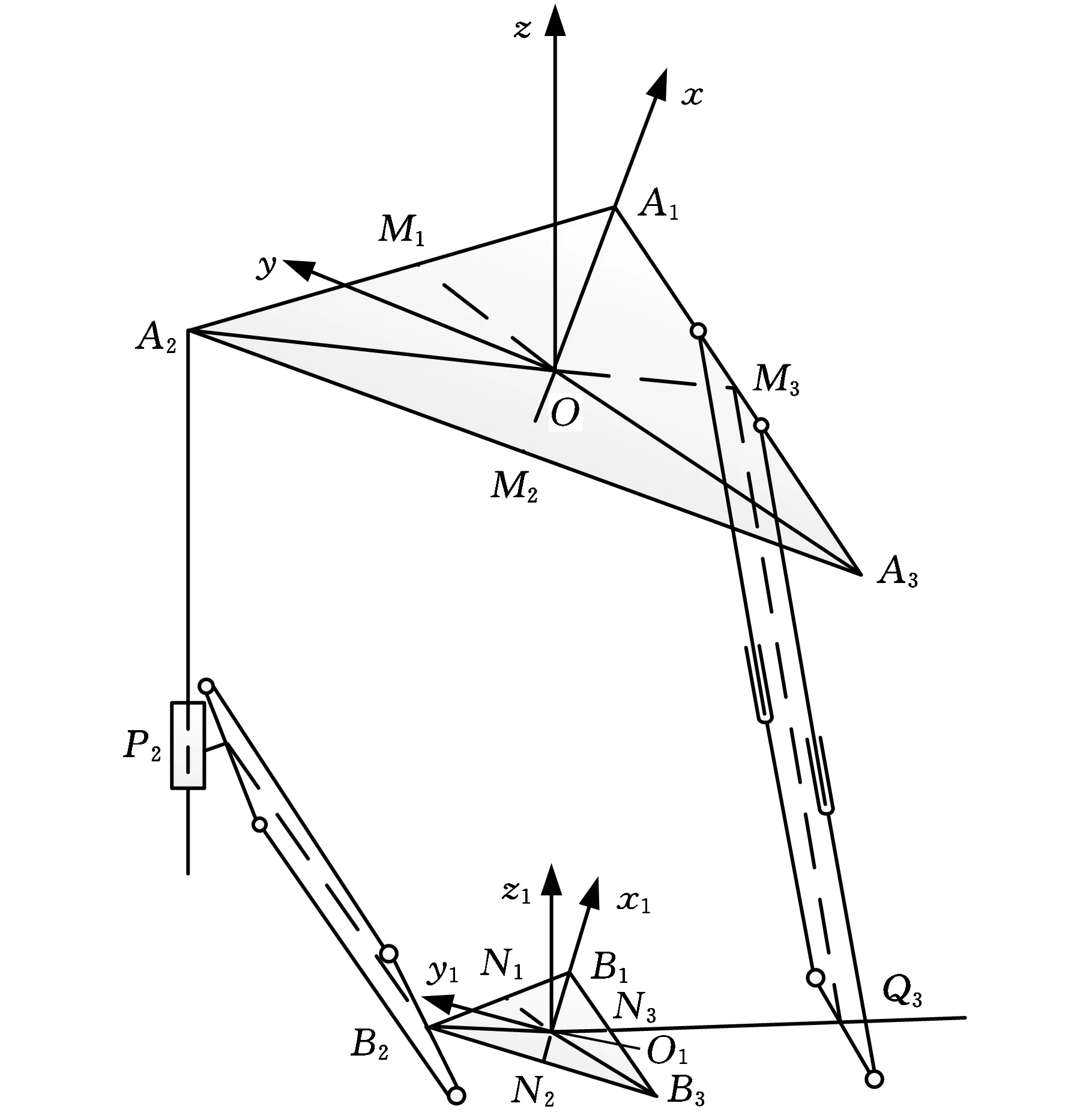
图2 定动平台及运动支链的几何位置关系
2 运动学分析
2.1位置反解分析
由向量OAn、AnPn、PnBn、BnO1、O1O构成主体机构的运动支链闭环,n=1,2,3。
在固定坐标系Oxyz中,An的位置坐标为
θn=2(n-1)π/3n=1,2,3
同样,在固定坐标系Oxyz中,Bn的位置坐标为
根据空间几何关系,令|AnPn|=Lbn,那么,点Pn在固定坐标系Oxyz中的位置矢量可以表示为
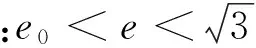
在固定坐标系Oxyz中,Mn的位置坐标为
γn=(2n-1)π/3n=1,2,3
同样,在固定坐标系Oxyz中,Qn的位置坐标为

(x+rcosθn-Rcosθn)2+
(1)
(x+dcosγn-Rcosγn)2+
(2)
为了满足动平台的运动设计要求,辅助机构每组对称分布的平行双联滚珠丝杠副对应的驱动关节径向输入速度应是一致的,将θn=2(n-1)π/3,γn=(2n-1)π/3代入式(1)和式(2)可得包含6个未知数的6个约束方程:
(3)
(4)
分析机构的运动学反解,可以确定驱动关节的位移范围,得到机构动平台运动范围即可达工作空间。工作空间的最高点和最低点应满足如下条件:
此时,动平台的几何中心在固定坐标系的z轴上。
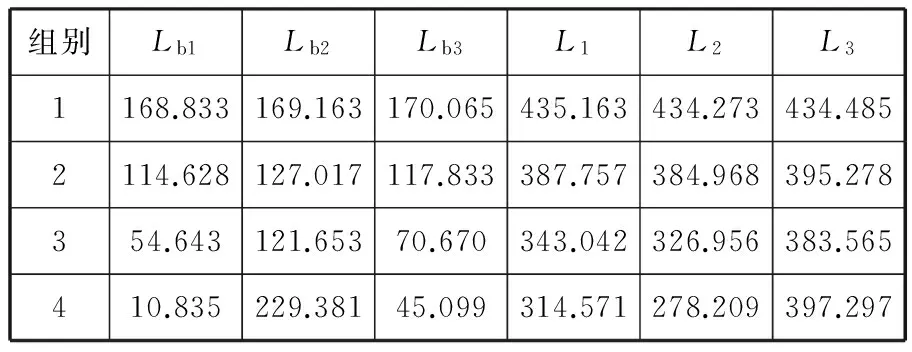
给定结构设计参数如表1所示。

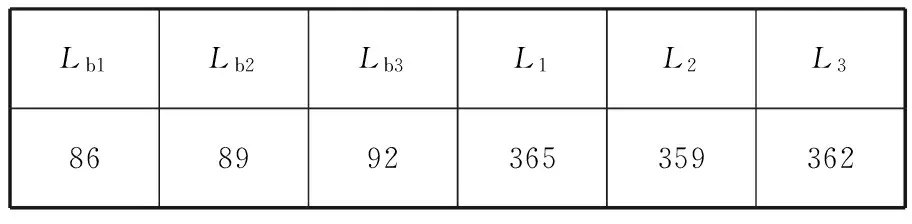
表1 多输出3D打印机器人机构设计参数 mm
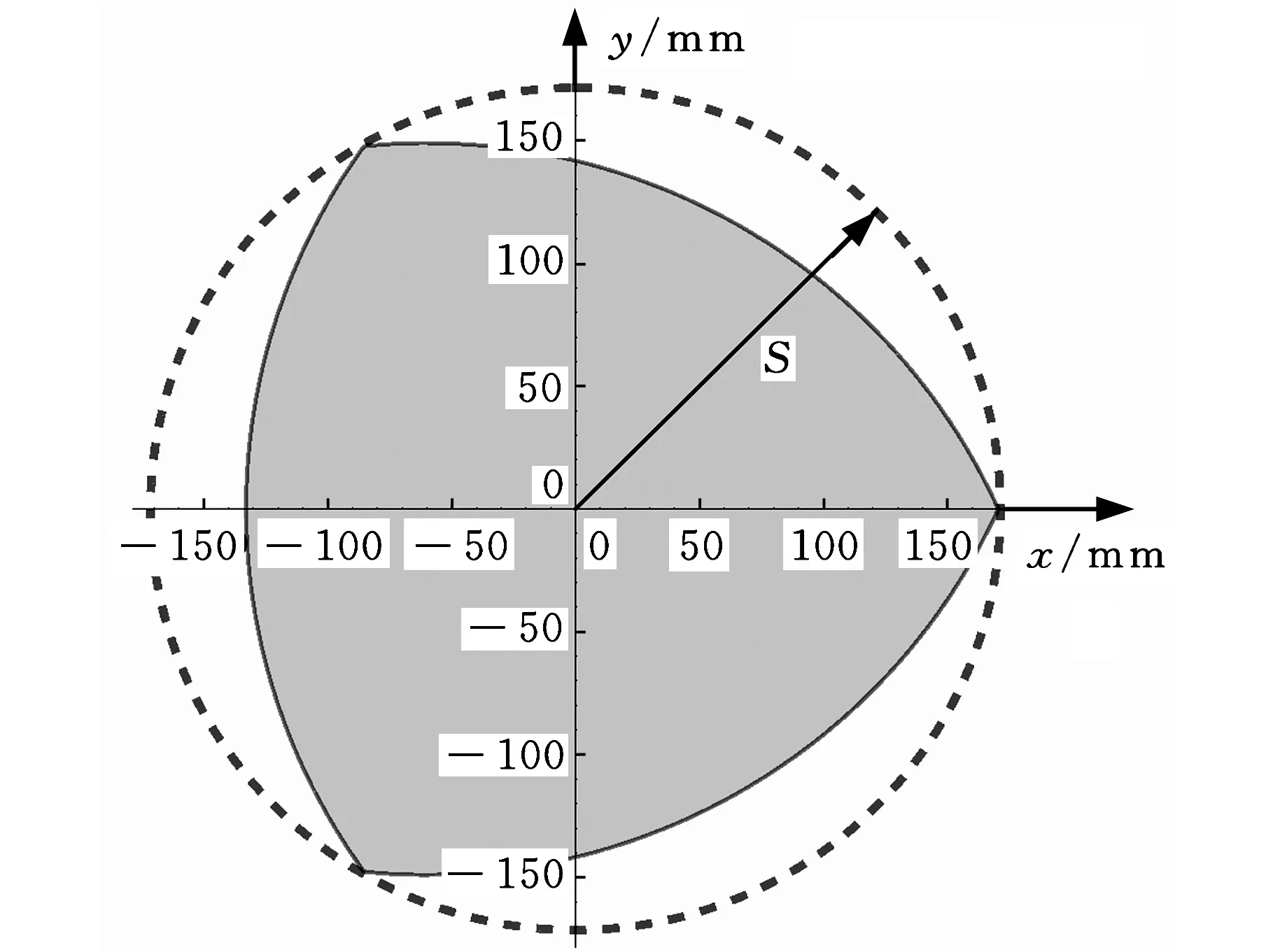
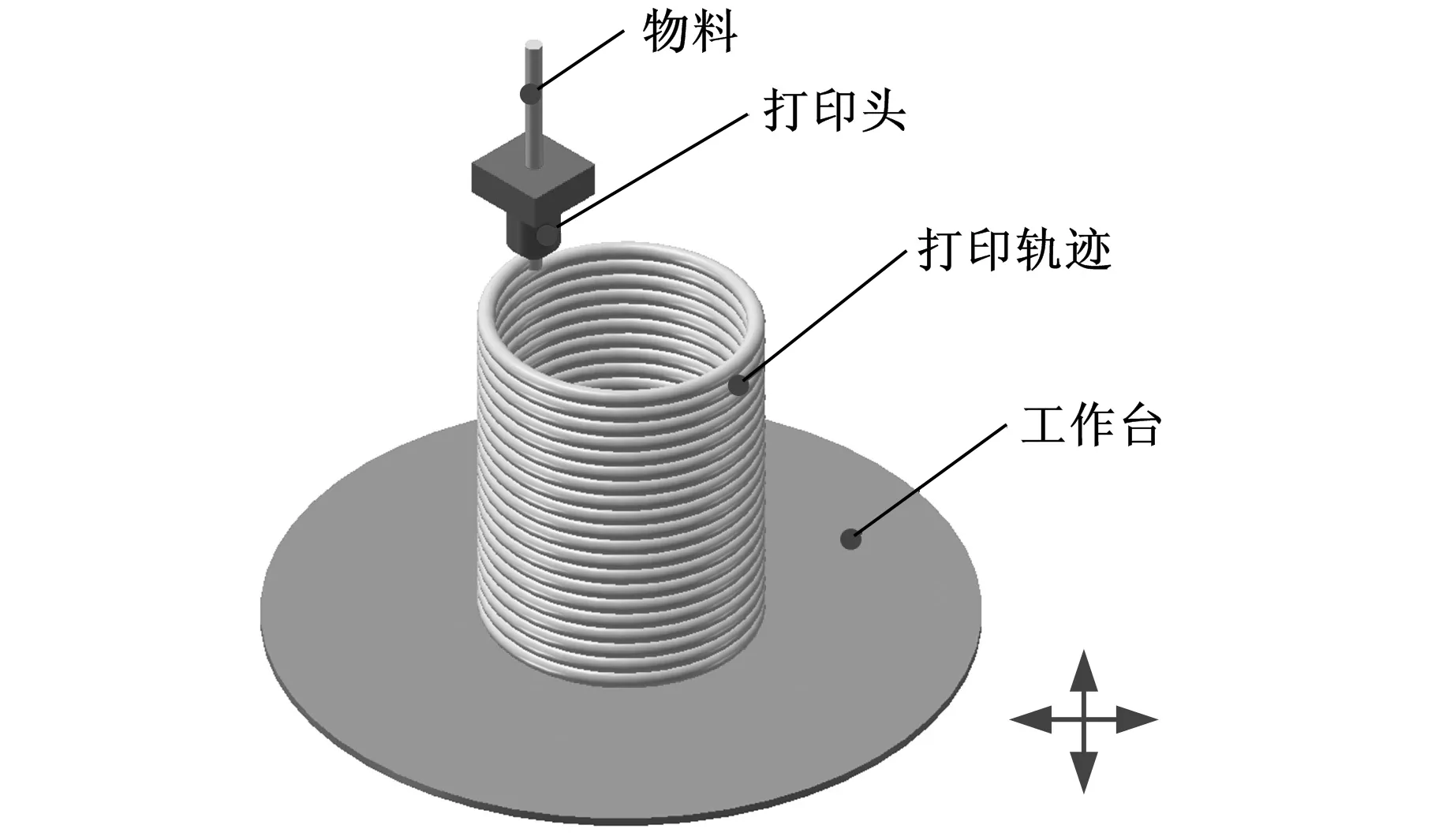
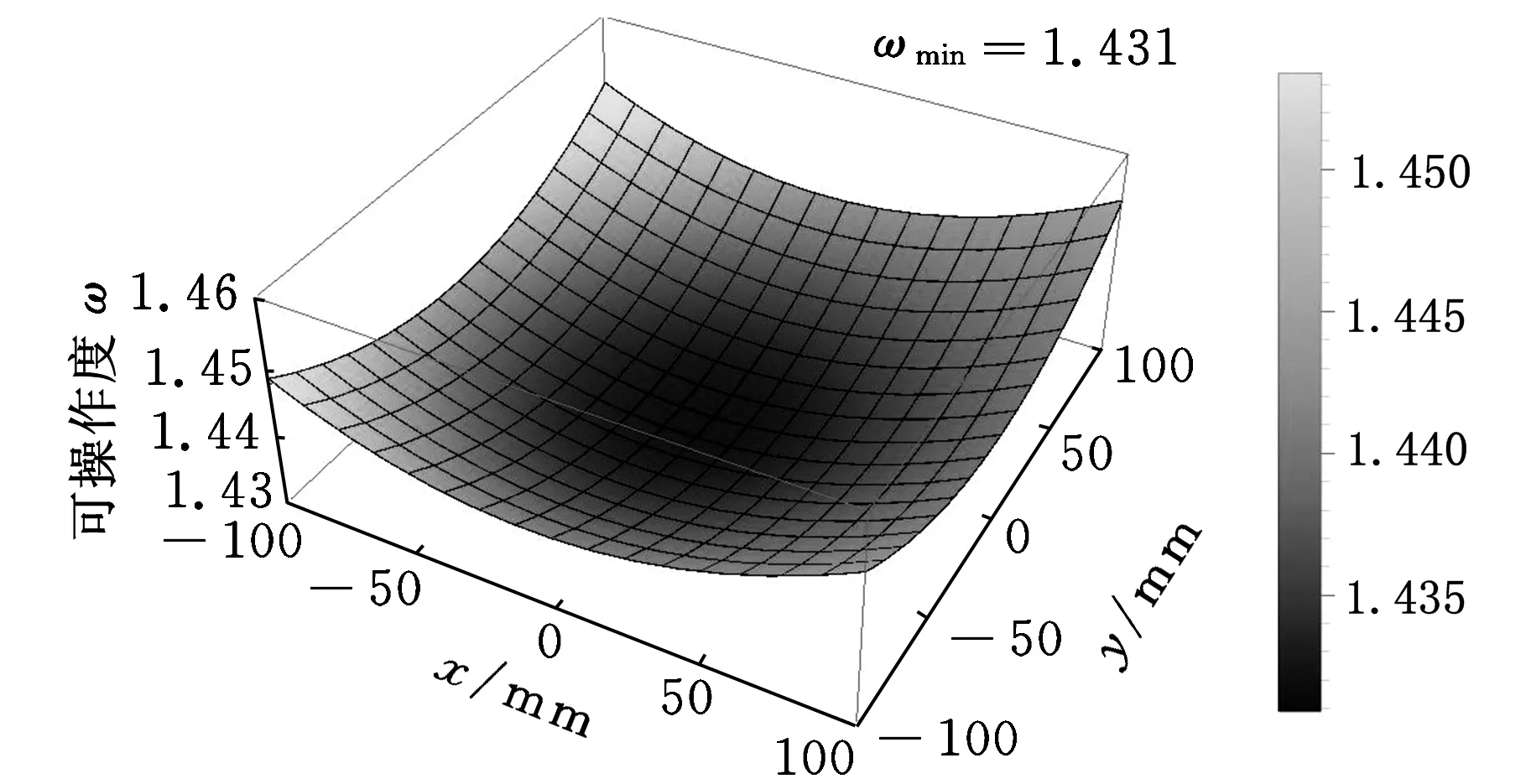
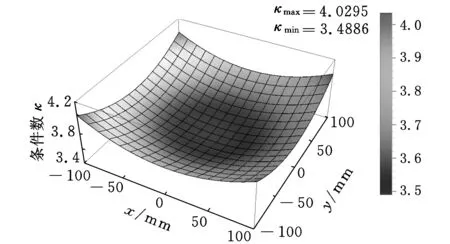
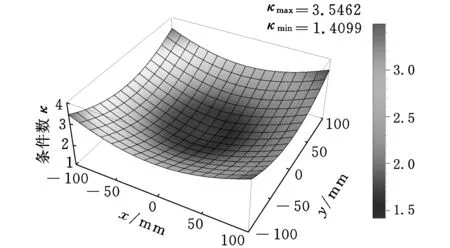
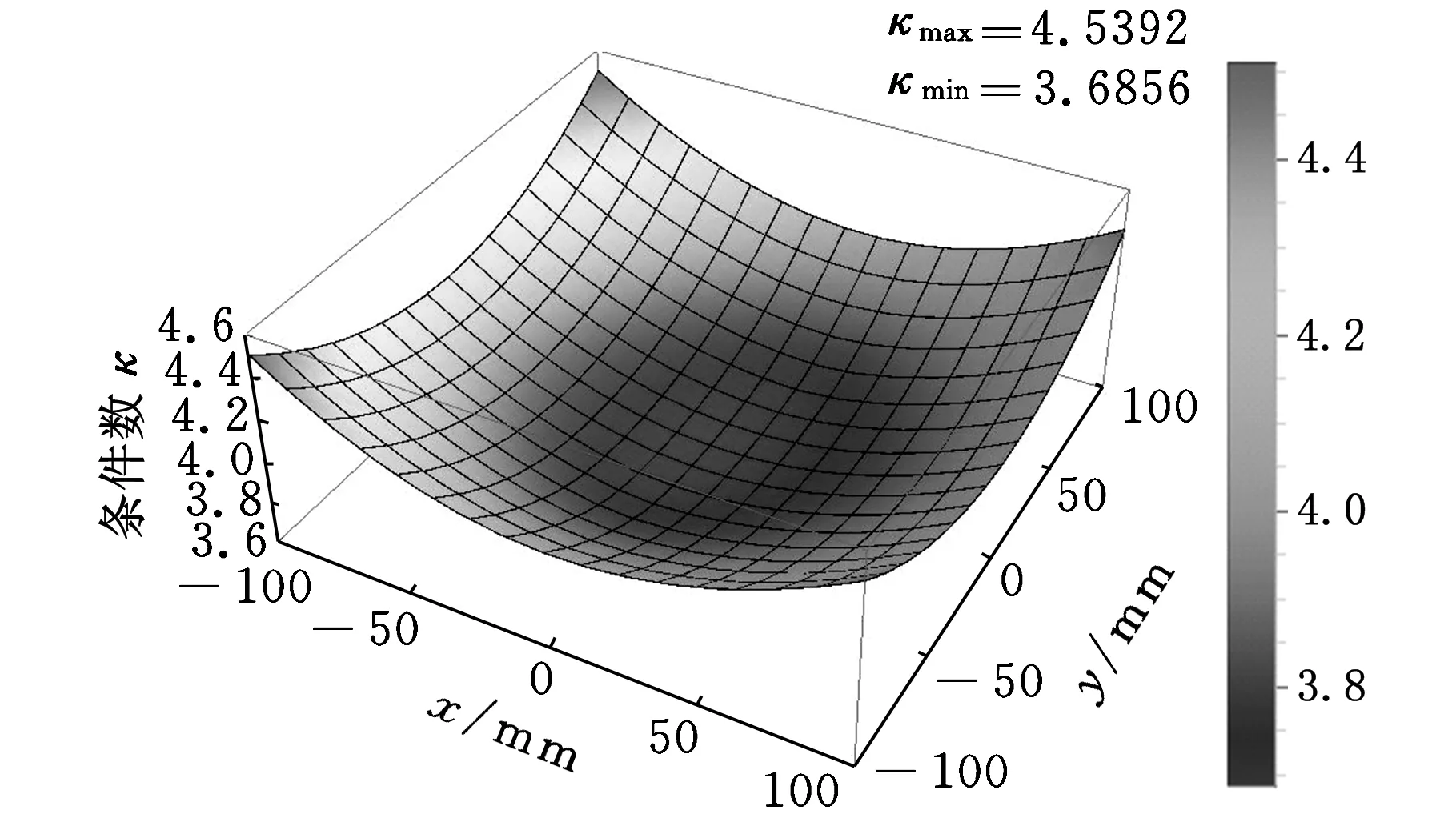
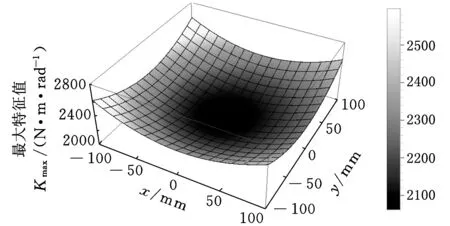
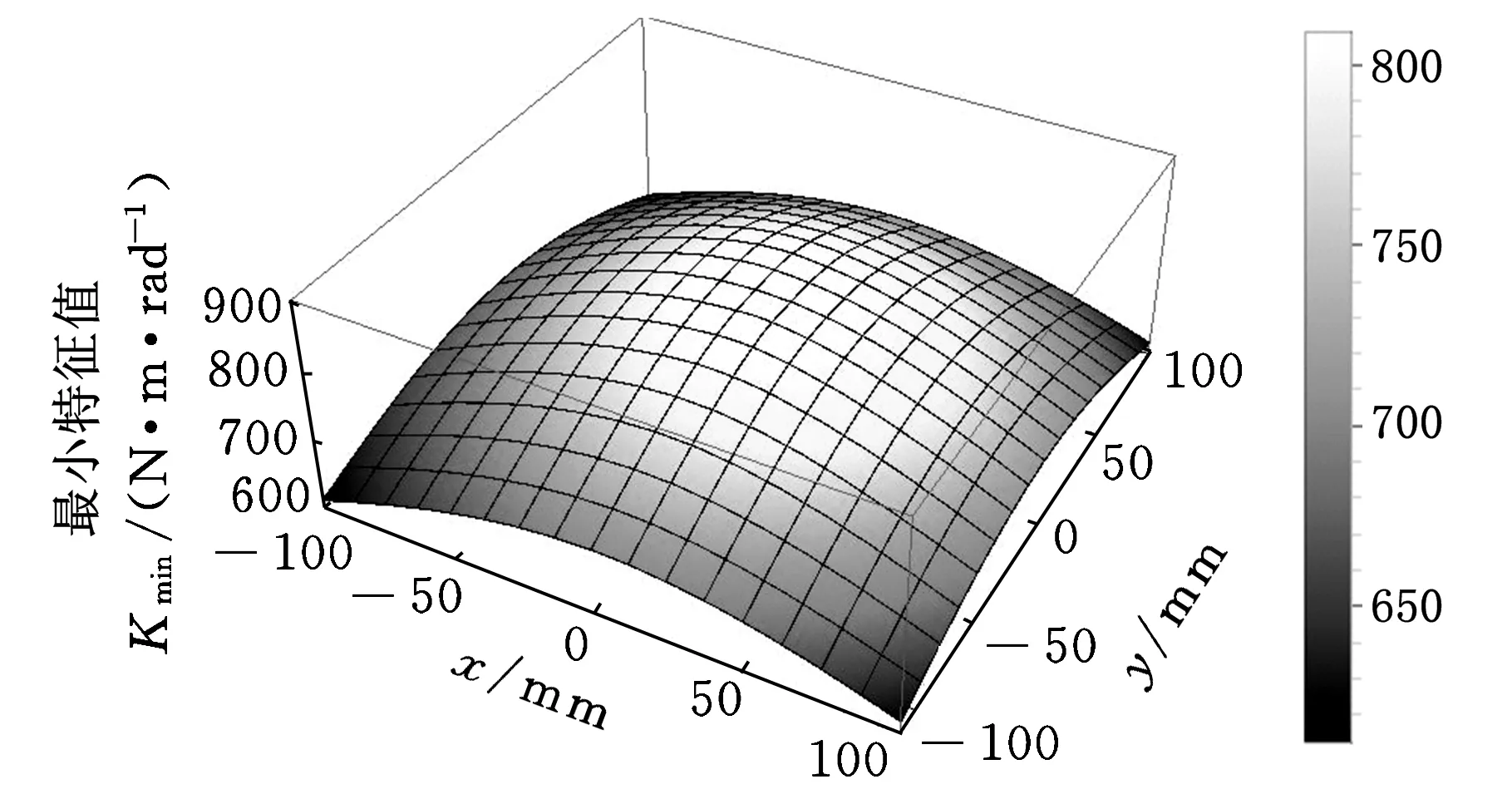
结合表1所给的设计参数及所建立的约束方程式(3)和式(4),求得该机构的可达工作空间边界曲面如图3所示。工作空间的最大截面与该截面上外接圆的关系如图4所示,外接圆半径为S。为避免刚性连杆与主体机构滚珠丝杆副的直线导轨发生干涉,刚性连杆的最大水平宽度为h(0 图3 打印机器人工作空间边界曲面 图4 工作空间最大截面与其外接圆的位置关系 给定机构动平台几何中心O1在可达工作空间内的位置坐标,如表2所示。结合式(3)和式(4)求得机构对应输入关节位置的数值解,如表3所示。 表2 动平台几何中心在固定坐标系下的位置坐标 mm 表3 机构输入关节位置的数值解 mm 根据机构给定的输入范围,求得的4组位置数值解符合设计要求。为了使两种组成机构的运动支链驱动机构动平台同步运动,需要分析输入关节速度和加速度的对应关系。 2.2雅可比矩阵分析 雅可比矩阵能够将动平台的运动速度与支链各个关节的瞬时运动速度和加速度相关联,这里主要分析驱动关节的运动速度和加速度。将式(1)对x,y,z,θn,Lbn分别求关于时间的偏导数,写成矩阵形式为 (5) 式中,J1为主体机构的雅可比矩阵。 将式(2)对x,y,z,γn,Ln分别求关于时间的偏导数,写成矩阵形式为 (6) 式中,J2为辅助机构的雅可比矩阵。 由式(5)和式(6)得到多输出3D打印机器人机构的速度雅可比矩阵为 (7) 那么有 (8) 当给定机构参数以及动平台速度时,由式(8)即可求得各支链驱动关节的瞬时输入速度。同样,其余各个关节的瞬时速度也可以根据此方法求得。 将式(5)和式(6)两边分别求关于时间的偏导数,即可得到加速度模型: (9) 由式(9)可知,各个支链的输入加速度的变化与其处于该位置时的输入速度和加速度都相关。 2.3运动仿真分析 为了满足打印机末端执行器在工作空间内的运动要求,设定打印机喷头直径为0.4 mm,给定一个打印头运动轨迹,如图5所示,为顺时针上升螺纹线,直径为60 mm,螺距为0.4 mm,圈数为20。根据设计要求,多输出3D打印机器人的4个打印头运动轨迹是一样的,如图6所示。打印头做速度为30 mm/s的匀速运动。 图5 设定的打印头运动轨迹示意图 图6 打印头运动轨迹 (a)主体机构驱动关节线位移 (b)主体机构驱动关节线速度 (c)主体机构驱动关节线加速度 图7主体机构输入关节线位移、速度和加速度随时间变化曲线 分析结果表明,在给定动平台的运动和轨迹时,主体机构和辅助机构的驱动关节位置、速度和加速度随时间的变化曲线是分别对应呈一定相位变化的。这样的变化是由各运动支链在动定平台上的相对位置决定的。将加速度变化曲线(图7c、图8c)与式(9)对比发现,机构不同支链相应驱动关节的加速度变化是一致的。若要实现机构驱动关节协调控制打印机的输出,必须精确控制打印机器人输入电机的运动。 (a)辅助机构驱动关节线位移 (b)辅助机构驱动关节线速度 (c)辅助机构驱动关节线加速度 图8辅助机构输入关节线位移、速度和加速度随时间的变化曲线 3.1奇异和灵巧性分析 机器人的可操作度定义为雅可比矩阵及其转置的乘积的行列式的开方[11],即 (10) 当ω=0时,机构处于奇异位置;当ω≠0时,机构处于非奇异位置。用机器人的可操作度来衡量机构的整体灵巧性。结合表1所给参数,给定输入关节变量数值,如表4所示。求得机构的可操作度ω值在工作空间截面z=-400 mm,z=-200 mm处的分布,如图9所示。可以看出ω最小值不为0,该机构不存在奇异位置,具有良好的可操作性能。 表4 3D打印机器人机构输入关节参数 mm (a)z=-400 mm (b)z=-200 mm图9 ω值在工作空间截面上的分布 (11) 将式(11)减去式(8)得到: (12) (13) 其中,‖J‖‖J-1‖即为雅可比矩阵的条件数,记为κ(J),且1<κ(J)<∞,κ(J)越大,机构输入速度变化对输出的影响越大;当κ(J)=1时,机构的运动传递性能最好。 目前常用谱范数计算矩阵的条件数定义为 (1) 本实验中光照强度的大小是通过控制____________来实现的;光合作用速率是通过____________反映出来的;产生的气泡中的气体主要是____________。 κ(J)=‖J‖‖J-1‖ (14) (15) 式中,x为任意列向量,其元素个数与J的列数相同。 对式(15)两边取平方可得 (16) ‖J‖2即为矩阵JTJ的最大特征值。如果J为非奇异矩阵,那么JTJ为正定矩阵,特征值都为正数。 (17) 在工作空间z=-400 mm,z=-200 mm截面上,机构条件数随着x、y变化,多输出3D打印机器人机构条件数分布如图10所示,主体机构的雅可比条件数分布如图11所示,辅助机构的雅可比条件数分布如图12所示。 (a)z=-400 mm (b)z=-200 mm图10 多输出3D打印机器人机构的雅可比矩阵条件数分布 (a)z=-400 mm (b)z=-200 mm图11 主体机构的雅可比矩阵条件数分布 (a)z=-400 mm (b)z=-200 mm图12 辅助机构的雅可比矩阵条件数分布 从图10~图12中可以看出,在接近截面的原点处κ值最小,机构的灵巧性最好,在工作空间截面边界处κ值最大,机构的灵巧性降低。多输出3D打印机器人机构雅可比矩阵J的条件数要小于主体机构的雅可比矩阵J1的条件数,稍大于辅助机构雅可比矩阵J2的条件数,具有良好的灵巧性。 3.2静刚度分析 对于并联机器人,其静刚度是指动平台处的输出刚度,刚度性能指标能评估机构运动关节的输入输出性能[12-13]。一般通过建立驱动传动系统的输入刚度与动平台的输出刚度之间的映射关系求解并联机器人的静刚度问题,在此过程中,假设各杆件是没有柔性的。 令τ=(τ1,τ2,…,τi)T为各个支链中主动副处的驱动力旋量,Δqi为相应关节的变形,χ=diag(k1,k2,…,ki),ki为等效弹簧常数,写成矩阵形式为 τ=χΔq 机器人机构的速度雅可比矩阵可以表示为 (18) 将式(18)用微分形式可表示为 Δq=JΔX (19) 式中,ΔX为动平台的微小变形。 并且定义动平台的等效力旋量F为 F=KΔX (20) 可以推导出: K=JTχ J (21) 可以看出机器人的刚度矩阵K也是对称矩阵,其结果与机构的驱动刚度和雅可比矩阵有关。因此,机器人机构的静刚度与机器人的位形参数和坐标系选择有关。 利用表1中的设计参数及表4中给定的机构输入参数,选取工作空间截面z=-300 mm,取等效弹簧系数k=1000,分析此时机构的静刚度矩阵的特征值随x、y的变化。多输出3D打印机器人机构、主体机构和辅助机构刚度矩阵最大特征值和最小特征值分布如图13、图14所示。 (a)机器人机构 (b)主体机构 (c)辅助机构图13 刚度矩阵最大特征值分布 (a)机器人机构 (b)主体机构 (c)辅助机构图14 刚度矩阵最小特征值分布 在实际情况中,为了使末端执行器在该工作空间截面上具有更高的精度,最小静刚度要大于某个特定值,一般选用最小特征值表示此位置机构的整体静刚度。从图13、图14中分析可知:①在此工作空间截面上,多输出3D打印机器人机构的刚度矩阵的最大特征值远大于主体机构和辅助机构的刚度矩阵最大特征值,说明此处3D打印机器人机构的动平台最大静刚度性能较好;②多输出3D打印机器人机构的刚度矩阵的最小特征值大于主体机构和辅助机构的刚度矩阵最小特征值,且远大于0,说明机器人机构相对于主体机构和辅助机构整体静刚度有所增大,能够提供更好的运动稳定性。 (1)通过建立的运动学反解约束方程,求得3D打印机器人机构的速度雅可比矩阵,将动平台的运动速度与支链各个关节的瞬时运动速度和加速度相关联。 (2)给定3D打印并联机器人执行器末端的运动速度和轨迹,通过仿真分析可反求得各个输入关节的运动速度,为实现机器人控制提供依据。 (3)结合雅可比矩阵分析可操作度和灵巧性,机构不存在奇异位置,具有良好的灵巧性。 (4)分析刚度矩阵,得到的结果满足设计要求,辅助机构在为刚性连杆提供拉力的同时,还能够提高设计机构动平台的稳定性及刚度。 [1]LipsonH,KurmanM.Fabricated:theNewWorldof3DPrinting[M].Indiana:JohnWiley&Sons, 2013.[2]WohlersT.AdditiveManufacturingand3DPrintingStateoftheIndustry[J].WohlersAssociates,FortCollins,CO, 2013(6):269-375. [3]DimitrovD,SchreveK,deBeerN.AdvancesinThreeDimensionalPrinting-stateoftheArtandFuturePerspectives[J].JournalforNewGenerationSciences, 2006, 4(1): 21-49. [4]KruthJP,LeuMC,NakagawaT.ProgressinAdditiveManufacturingandRapidPrototyping[J].CIRPAnnals-ManufacturingTechnology, 1998, 47(2): 525-540. [5]RandallNewton. 3DSystemsShipsProjectSD3000forIn-office3DPrinting[J].EngineeringAutomationReport, 2008, 17(9):294-300. [6]LemuHG,KurtovicS. 3DPrintingforRapidManufacturing:StudyofDimensionalandGeometricalAccuracy[M].Berlin,Heidelberg:Springer, 2012. [7]RepRapWiki.FuturePlans[EB/OL]. [2010-05-02].http://reprap.org/wiki/FuturePlans. [8]Wikipedia.Fab@Home[EB/OL].[2014-01-26].http://en.wikipedia.org/wiki/Fab@Home. [9]LiptonJI,CohenD,HeinzM,etal.Fab@homeModel2:TowardsUbiquitousPersonalFabricationDevices[C]//SolidFreeformFabricationSymposium.Austin,2009: 70-81. [10]MikeSzczys. 3DPrintingwithaDeltaRobotthatSeemstoSimplifytheConcept[EB/OL].[2012-07-13].http://hackaday.com/2012/07/13/3d-printing-with-a-delta-robot-that-seems-to-simplify-the-concept. [11]TsaiLW.RobotAnalysis:theMechanicsofSerialandParallelManipulators[M].NewYork:JohnWiley&Sons, 1999. [12]JoshiS,TsaiLW.AComparisonStudyoftwo3-DOFParallelManipulators:OnewithThreeandtheOtherwithFourSupportingLegs[J].RoboticsandAutomation,IEEETransactionson,2003, 19(2): 200-209. [13]SadjadianH,TaghiradHD.Kinematic,SingularityandStiffnessAnalysisoftheHydraulicShoulder:a3-DOFRedundantParallelManipulator[J].AdvancedRobotics, 2006, 20(7): 763-781. (编辑袁兴玲) Design and Analysis of a Multiple Output 3D Printing Redundant Parallel Manipulator Chang DingyongFang Yuefa Beijing Jiaotong University,Beijing,100044 A multiple output 3D printing robot was designed. The main configuration of this robot was Delta parallel manipulator, the Stewart parallel manipulator was served as an auxiliary configuration. In order to achieve multiple output ability, more extruders on the end effector of the robot were arranged. Based on the established kinematics model, the inverse kinematics of the proposed redundant parallel manipulator was analyzed and the velocity Jacobian matrix was obtained. Then, the velocity and acceleration of each actuated joint were solved.The motion coordination of the mechanism with a prescribed motion trajectory was analyzed, which was based on the simulation model. In addition, dexterity and static stiffness of the mechanism were analyzed. 3D printing robot; parallel manipulator; the Jacobian matrix; dexterity;static stiffness 2015-01-28 国家自然科学基金资助项目(51175029);北京市自然科学基金资助项目(3132019) TH112< class="emphasis_italic">DOI :10.3969/j.issn.1004-132X.2015.12.005 常定勇,男,1988年生。北京交通大学机械与电子控制工程学院硕士研究生。主要研究方向为并联机构运动学、动力学及控制。方跃法,男,1958年生。北京交通大学机械与电子控制工程学院教授、博士研究生导师。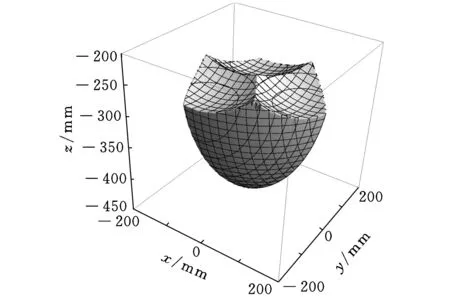

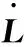
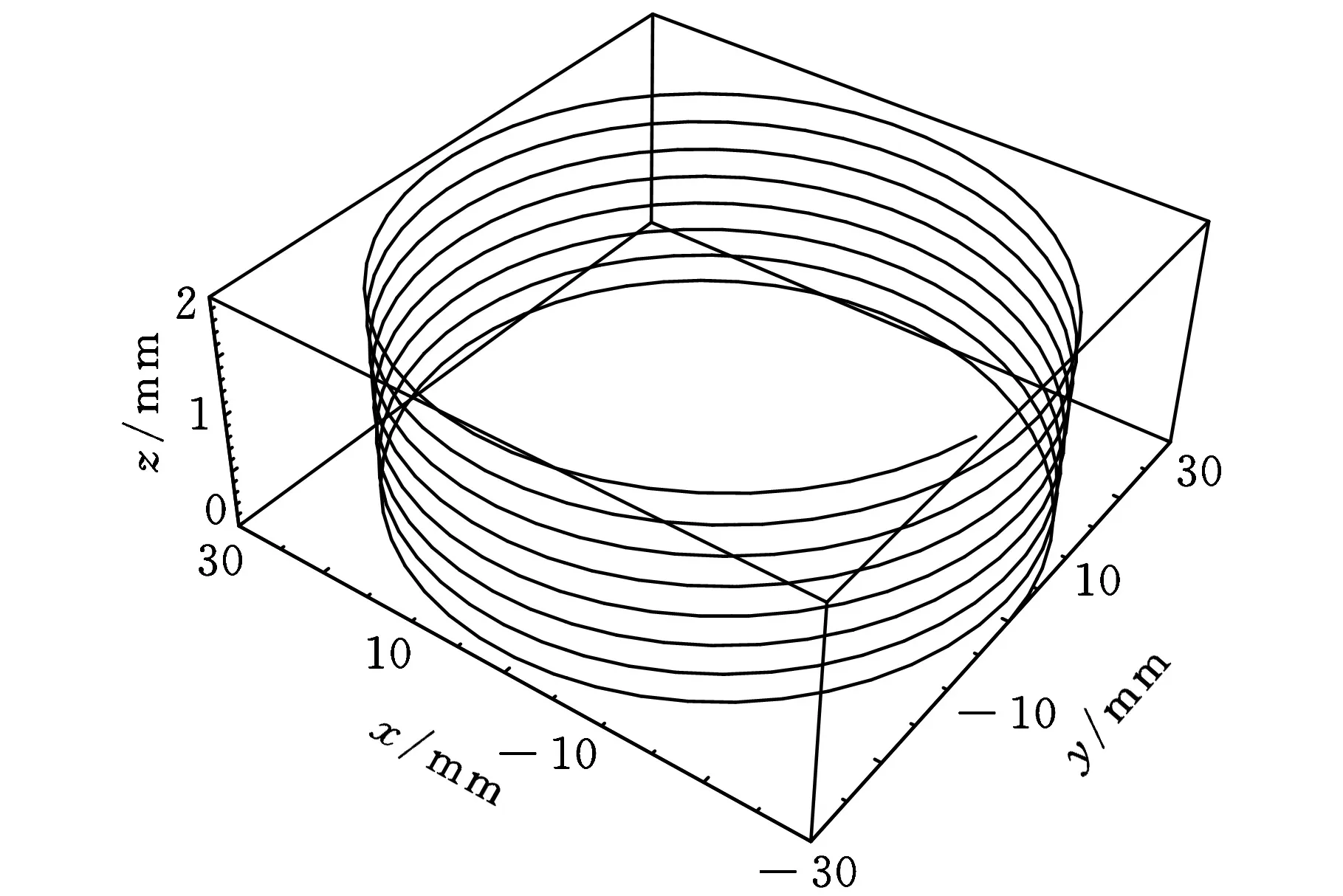

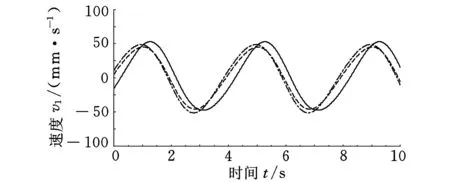
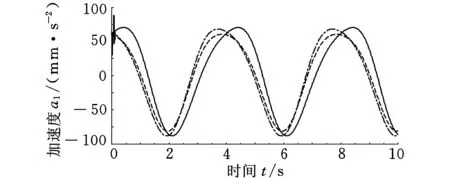

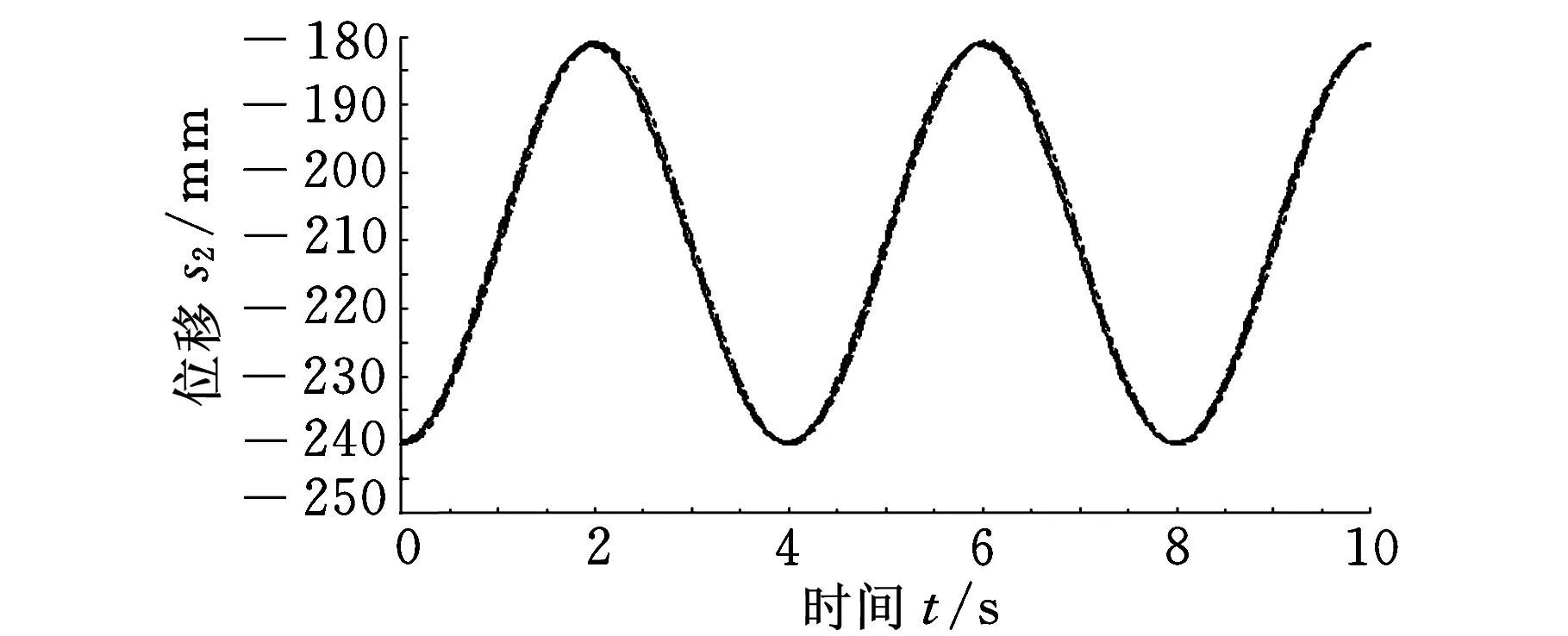
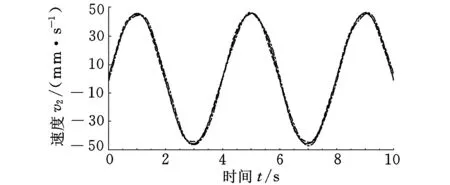
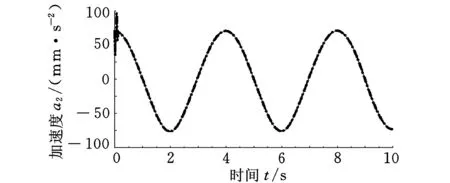

3 运动性能分析

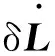
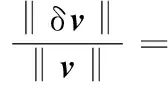
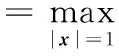
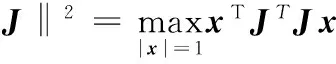







4 结论
