一种过约束并联机构受力的数值仿真分析方法

赵永生　刘文兰　许允斗　姚建涛　金林茹，3

1.燕山大学河北省并联机器人与机电系统实验室,秦皇岛,0660042.燕山大学先进锻压成型技术与科学教育部重点实验室,秦皇岛,0660043.北京机电院机床有限公司,北京，100027

一种过约束并联机构受力的数值仿真分析方法

赵永生1,2刘文兰1许允斗1,2姚建涛1,2金林茹1，3

1.燕山大学河北省并联机器人与机电系统实验室,秦皇岛,0660042.燕山大学先进锻压成型技术与科学教育部重点实验室,秦皇岛,0660043.北京机电院机床有限公司,北京，100027

鉴于目前对过约束并联机构进行受力仿真分析的研究非常少，提出了一种对该类机构受力的数值仿真分析方法。将机构的动平台、定平台及所有运动副视作刚体，将易产生空间复合弹性变形的分支杆视为柔性体，用虚拟关节代替外形复杂的运动副模型，结合三维建模软件、ANSYS软件及ADAMS软件建立与理论模型完全一致的刚柔混合模型；仅改变驱动量使机构运动到指定位形，便能实现对机构在任意位形下的受力分析，避免了对机构的不同位形重建模型。采用该方法对三种类型的过约束并联机构进行了受力分析，分析结果验证了该方法的正确性，同时也表明该方法具有一定的通用性，且无需复杂的理论计算，便能获得过约束并联机构在任意位形下的驱动力和各关节约束反力大小，为此类机构的受力分析提供了便捷途径。

过约束并联机构;数值仿真;受力分析;刚柔混合模型

0　引言

对于一个并联机构，当其分支含有公共约束或机构中存在冗余约束时我们将其称为过约束并联机构，这类过约束也称为被动过约束[1],本文提到的过约束机构指被动过约束并联机构。

当过约束并联机构中需要求解的未知力个数超过了可列出的独立平衡方程数时,该类机构的受力分析就非常困难，属于静不定问题。国内外关于过约束并联机构受力分析的文献相对比较少,董军等[2]对具有虚约束的平行四边形机构进行了受力分析,Huang等[3]基于反螺旋理论分别对含有过约束线矢力的4-R(CRR)(R和C分别表示转动副和圆柱副)对称四自由度并联机构进行了动力学分析，赵燕等[4]对含过约束力偶的4-UPU(U和P分别表示虎克铰和移动副)对称四自由度并联机构进行了动力学分析，文献[5-6]对每个支撑分支只提供单维轴向约束力的过约束并联机构进行了静力学分析。但是，这些关于过约束并联机构受力方面的研究文献大多是理论分析，其计算过程往往较为复杂，不易于快速掌握，限制了其应用。

虽然目前应用仿真软件对并联机构进行受力分析仿真验证或其他方面的研究已经不少,但对象大多是非过约束并联机构[7-9],对此只需建立刚体模型。然而，对于过约束并联机构，在其刚体模型上添加运动副造成过约束后,ADAMS软件在仿真过程中会自动添加多余自由度将公共约束或冗余约束解除[10],使其转化为非过约束机构。因此,非过约束并联机构的受力仿真研究方法已不适用于过约束并联机构。求解过约束并联机构的关节约束反力和驱动力需要结合变形协调方程，故应建立这类机构的刚柔混合模型对其进行受力仿真研究。目前已有的关于建立刚柔混合模型的研究仅针对一些非过约束机构[11-12],或者是并非以过约束机构的受力分析为研究内容的机构学研究[13],鲜有建立过约束并联机构刚柔混合模型并开展受力仿真分析的文献报道。

ANSYS软件虽然能建立机构的刚柔混合模型,但其静力分析模块中无法直接驱动刚柔混合模型，只能在确定位形下分析机构的受力情况，若分析该机构在其他位形的受力，则需要重建模型,使分析过程变得繁琐。ADAMS仿真软件不仅可以通过添加驱动使机构运动到任意指定位形，而且可直接测量关节约束反力在任意坐标轴上的分量[14],对过约束并联机构的受力分析非常方便。因此，本文将联合三维建模软件、有限元分析软件ANSYS和多体动力学仿真软件ADAMS,提出一种建立过约束并联机构刚柔混合模型的方法，并对三种不同类型的过约束并联机构进行受力数值仿真，求解机构各关节约束反力和驱动力大小。

1　一种过约束并联机构受力的理论分析方法简介

为了便于验证本文提出的数值仿真方法的正确性，在此先引用一种过约束并联机构受力分析的理论方法[1]。

该理论方法的步骤如下：

(1)基于反螺旋理论分析各支撑分支提供给动平台的约束力螺旋系。

(2)依据力递推法，求解支撑分支在其约束力螺旋系作用下所有运动副的约束反力；利用材料力学基础知识，从支撑分支末端到基座依次求解各分支杆在运动副约束反力作用下引起的分支末端变形。

(3)将各分支杆引起的分支末端变形叠加即可得到分支末端的总弹性变形，分支约束力螺旋系幅值大小与该总弹性变形在分支各约束力螺旋轴线方向的投影大小之间的映射矩阵即为该支撑分支的约束力螺旋系刚度矩阵。

(4)结合各分支末端变形与动平台微位移之间的变形协调关系以及动平台的受力平衡方程即可求得机构的整体刚度矩阵。

(5)利用机构整体刚度矩阵和各分支约束力螺旋系刚度矩阵可求得各分支提供给动平台的约束力螺旋系幅值(包括驱动力)大小。

2　过约束并联机构受力分析的数值仿真方法

该数值仿真方法的一般步骤为：利用三维建模软件建立过约束并联机构的简易刚体模型;利用ANSYS软件建立所有分支杆的柔性体；利用ADAMS软件建立机构的刚柔混合模型并添加驱动及外力;进行静力学仿真并测量各关节约束反力；改变驱动值分析其他位形下机构的受力情况。其流程如图1所示。

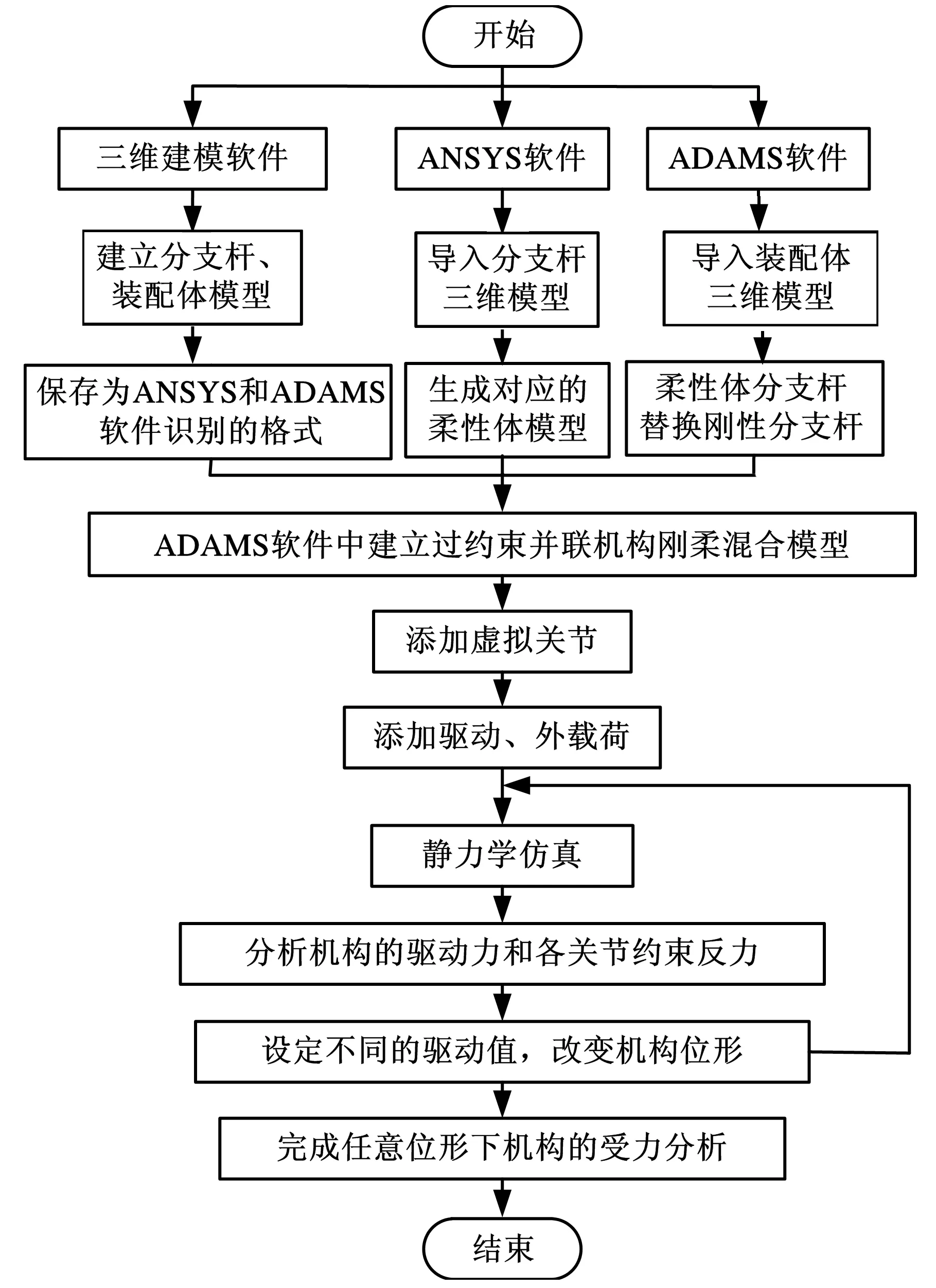
图1　数值仿真方法的流程

2.1建立三维模型

利用三维建模软件建立过约束并联机构的动平台、定平台以及所有分支杆模型，由于在整个受力分析过程中主要考虑的是分支杆的变形，所有运动副被视作刚体,又因在ADAMS仿真软件中用虚拟运动副代替真实运动副连接两构件并不影响机构运动和力的传递，即使不存在真实的运动副模型，亦能通过测量虚拟运动副得到所有关节力大小，因而本文在三维建模时不再建立外形复杂的运动副模型。零部件建模完成后按照D-H法规定的机构各运动副轴线位置、方向等条件进行装配，保证装配体具有机构正确的自由度。对于装配中出现的如图2所示的干涉现象无需处理,这种干涉在ADAMS软件中不影响过约束机构的静力分析结果。以3-RRC(R表示驱动加在此转动副处)三平移过约束并联机构[15]为例,其三维简易刚体模型如图3所示。最后将机构的装配体和所有分支杆保存为ANSYS软件和ADAMS软件能识别的格式。

图2　三维模型中的干涉现象图3　3-RRC过约束机构的三维简易模型

需要指出的是,后续仿真分析结果说明本文提出的方法在三维建模时对运动副的简化处理可行,它使得该方法建模过程简单快速，最终所建模型与一般理论分析模型一致，易于和理论方法之间互相验证。

2.2建立支撑分支中各杆件的柔性体

图4　分支杆端面的刚化处理

按照ANSYS软件中生成有限元模型的步骤将需要柔性化的各分支杆进行网格划分,并进行模态计算，最终输出ADAMS软件能识别的模态中性文件。在此需要说明两点:①本文提出的数值仿真方法分析的是过约束并联机构在受到六维外力作用时，机构的驱动力和各关节约束反力大小，故建立柔性体分支杆时，给杆件赋予非常小的密度值，即忽略杆件的重力；②该方法中将过约束并联机构的动平台和定平台以及所有运动副均视作刚体，在柔性杆与柔性杆之间、柔性杆与动定平台之间添加运动副的地方需对柔性杆进行刚化处理,图4所示为对3-RRC机构的各分支杆两端需加转动副(圆柱副)的地方进行刚化处理的结果。

2.3建立刚柔混合模型

首先,将三维建模软件保存的机构装配体导入ADAMS软件并添加虚拟运动副，此时完成的过约束并联机构模型为全刚性的,图5所示为3-RRC过约束并联机构的刚体模型。其次,用ANSYS软件中生成的柔性杆替换刚体模型中对应的分支杆，并重新在柔性杆与柔性杆、柔性杆与动定平台之间添加虚拟关节。最后，对过约束并联机构的刚柔混合模型添加驱动与外载荷。图6所示为添加了虚拟关节、驱动及外载荷的3-RRC过约束并联机构的刚柔混合模型。

图5　3-RRC过约束并联机构的刚体模型

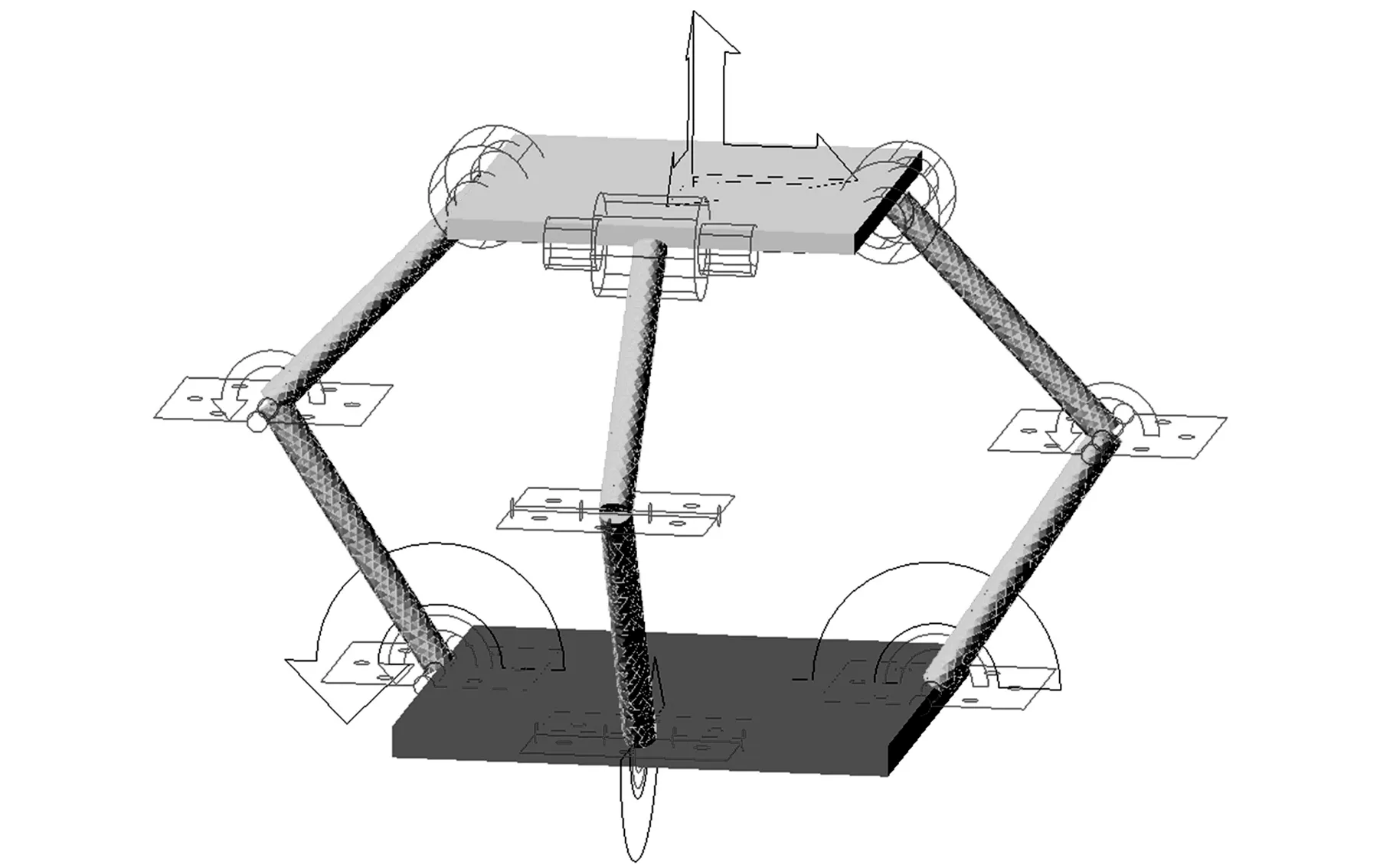
图6　3-RRC过约束并联机构的刚柔混合模型

2.4过约束并联机构关节约束反力/力矩和驱动力的测量

图7　被测关节处建立marker坐标系oxyz

ADAMS软件中marker点起到局部坐标系的作用,为方便测量机构某方向的关节约束反力大小,先在该关节处添加一个marker坐标系oxyz，如图7所示。

静力学仿真结束后，通过图8所示的测量方法即可得到各关节约束反力(包括驱动力)在任意参考坐标系下的分量大小或总幅值大小。需要强调的是：分支驱动力与其他关节约束反力解耦时，沿驱动力方向的测量结果即为驱动力大小,反之,对测量结果进一步计算才能得知驱动力大小。例如3-RRC机构各分支提供给动平台2个约束力偶作用,分支中驱动力线矢沿靠近动平台的分支杆轴线方向,它与2个约束力偶解耦,故沿图7所示marker坐标系z轴方向的测量结果即为该分支驱动力线矢的大小。

图8　测量某方向的约束力

2.5任意位形下机构的约束力分析

图9　3-RRC机构水平移动后其刚柔混合模型

在ADAMS软件中只需改变驱动副的输入量，驱动过约束并联机构的刚柔混合模型运动到其他位形，便可实现对过约束并联机构在任意位形下的静力分析。ANSYS软件的静力分析模块只能在已完成的装配位形下对刚柔混合模型进行受力分析，若要分析机构在其他位形下的受力情况还需重新调整原始装配体，该软件的静力分析模块中不能直接驱动刚柔混合模型运动，故本文提出的过约束并联机构受力的数值仿真方法采用在ADAMS软件中建立其刚柔混合模型的方法。例如,改变3-RRC过约束机构的驱动输入值，使动平台发生水平移动后其刚柔混合模型如图9所示，进而可分析此位形下3-RRC机构的驱动力和约束力大小。

3　基于数值仿真法的过约束并联机构受力分析实例

为说明采用该方法对过约束并联机构受力进行分析的通用性，选取三种不同类型的过约束并联机构进行数值仿真分析并应用前面引用的理论方法进行验证。这三种机构的不同体现在过约束情况不同，它们分别是各分支对动平台仅提供约束力偶的空间3-RRC机构、仅提供约束力的空间7-SS结构以及既提供约束力又提供约束力偶的平面五杆四边形机构。

3.13-RRC过约束并联机构的受力分析

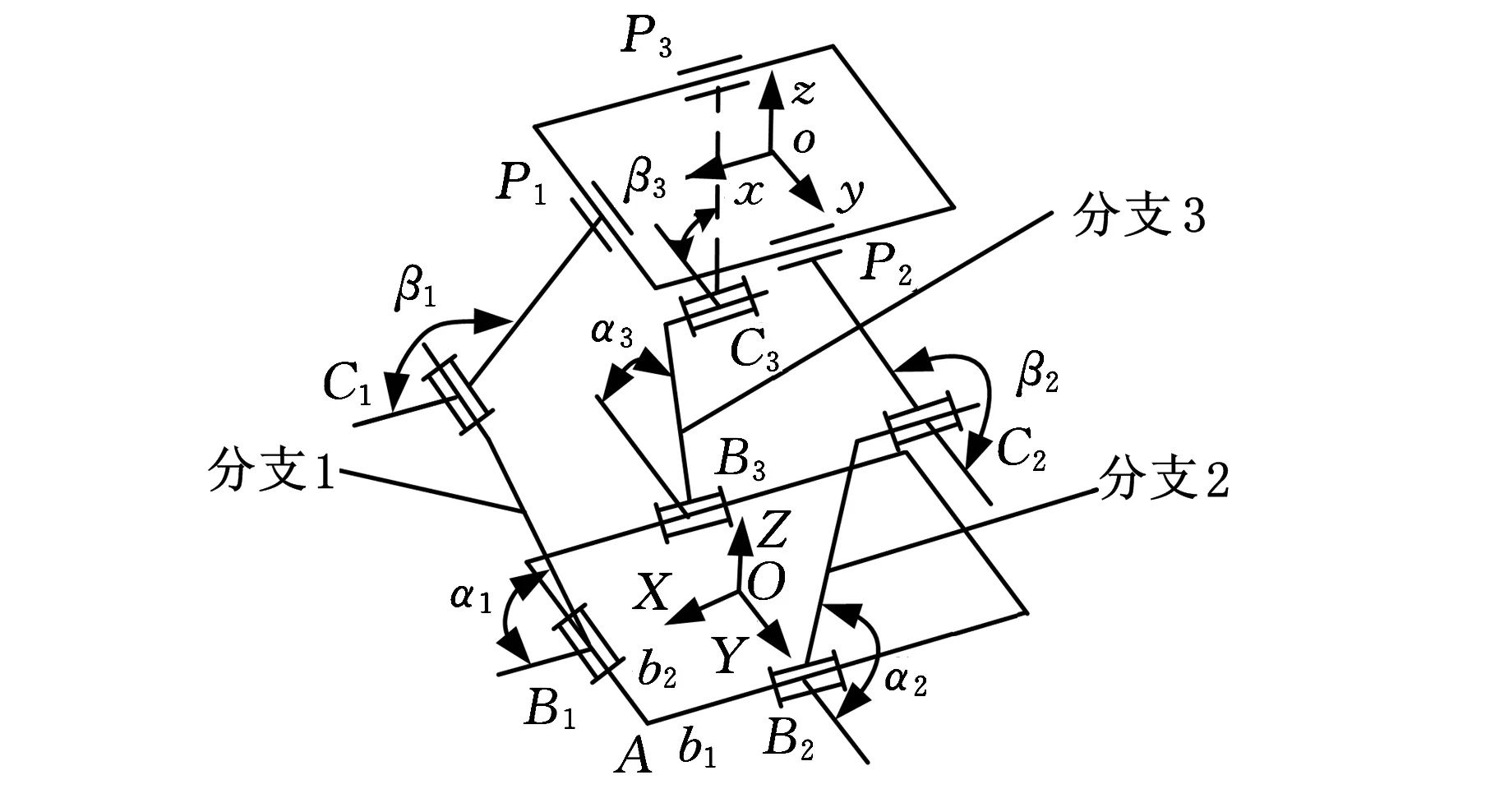
图10　3-RRC过约束并联机构简图

空间3-RRC三平移并联机构如图10所示,该机构由三个相同的分支各通过一个C副和两个R副连接动、定平台组成，与定平台相连的转动副R为驱动副。每个分支的三个运动副轴线相互平行，且都平行于定平台B1B2B3,分支二和分支三的运动副轴线之间也相互平行。根据螺旋理论基本知识可判断出该机构每个分支提供给动平台2个垂直于分支运动副轴线的约束力偶，这6个约束力偶线性相关，其最大线性无关数为3，故该机构有3个冗余约束，属于过约束并联机构。根据文献[16]中驱动力螺旋的定义可知，每个分支还提供给动平台一个过分支中第二个转动副中心且沿靠近动平台的分支杆轴线方向的驱动力线矢，从物理意义上讲，该驱动力线矢就是由分支驱动副施加给动平台的1个约束力线矢，其大小与驱动副的驱动力矩大小之间满足一不定的关系[17]。因此，该机构的每个圆柱副共受到2个约束力偶和1个驱动力线矢作用。接下来用本文提出的数值仿真方法分析该机构的6个约束力偶和3个驱动力线矢的大小。

给定该机构的一组结构尺寸:6根圆柱杆横截面直径均为0.016 m，杆长均为0.15 m,图10中b1=0.15 m,b2=0.02 m,其中，b1、b2分别表示转动副中心B1、B2到定平台顶点A的距离。建立该机构的刚柔混合模型，如图5所示。建立图10所示的定坐标系OXYZ和动坐标系oxyz,取各分支转角α1=α2=α3=57°为该机构的初始位形。动坐标系下施加6维外力F=(10 N,15 N,-20 N,9 N·m,-10 N·m,15 N·m)T，静力学仿真结束后，定坐标系下测量可得到各分支提供的2个约束力偶大小,在图7所示marker坐标系z轴方向测量即可得到驱动力线矢大小。

为了验证仿真结果的正确性，用本文第1节中引用的理论分析方法[1]对3-RRC过约束并联机构进行受力计算,并将得到的理论值与仿真值进行误差分析。各分支提供给动平台的约束力偶和驱动力线矢幅值的仿真值、理论值及误差分析结果如表1所示，其中误差为仿真值与理论值的差值与理论值的比值。

表1　3-RRC机构初始位形下各力的仿真值与理论值

注:表中数据仅表示各力大小,不包括方向。

从表1可以看出,本文提出的数值仿真方法对3-RRC过约束并联机构的受力分析结果与理论分析结果之间误差小于1%,充分验证了该方法的正确性。

本文提出的过约束并联机构受力的数值仿真分析方法不仅能获得机构处于某一位形时各力的大小，而且可以很方便地分析机构在运动过程中各驱动力和约束力的变化情况及具体大小。以3-RRC三平移过约束并联机构为例，在ADAMS仿真软件中调整该机构刚柔混合模型的三个驱动输入量,使动平台按照轨迹y(m)=0.01t沿定坐标系Y轴运动2 s(在这2 s的运动过程中该机构未出现奇异位形),运动结束时刻机构所处位形如图9所示，根据本文提出的数值仿真方法即可获得在上述2 s的运动过程中3-RRC机构各分支驱动力线矢和约束力偶幅值的变化情况及大小，其仿真结果如图11所示。

(a)分支1各力仿真值

(b)分支2各力仿真值

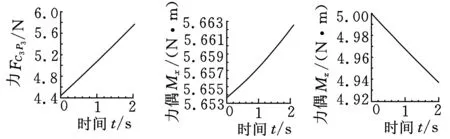
(c)分支3各力仿真值图11　3-RRC机构沿Y向运动过程中各力仿真值

为了验证上述运动过程中得到的各力仿真曲线的正确性，可以针对3-RRC机构在整个运动过程中所处的一系列位形按照本文引用的理论方法[1]进行计算，得到理论曲线后与仿真曲线进行误差比较。这里我们给出t=2 s时刻机构各分支的驱动力线矢和约束力偶幅值的仿真值与理论值及误差分析结果,如表2所示。

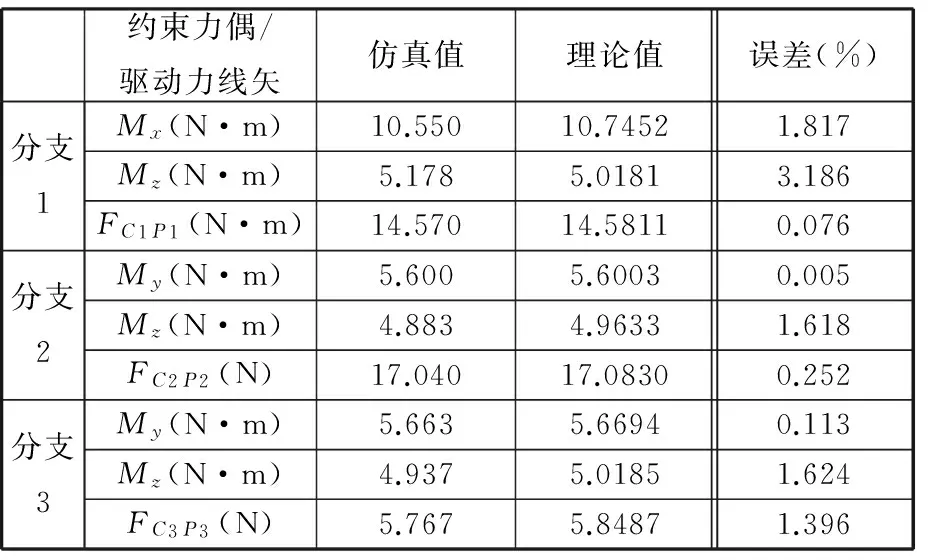
表2　3-RRC机构在图9位形时各力的仿真值与理论值

从表2可以看出,该位形下受力分析的仿真结果与理论计算结果之间误差也很小。

同理，可分析该机构处于任意位形时的受力情况。3.27-SS过约束并联结构的受力分析

预紧式6-1/3-3-1型Stewart结构力传感器结构简图见图12，该机构由下平台、上平台和7个分支DiUi(i=1,2,…,7)组成,各分支均通过S副与上下平台连接,每个分支施加给上平台1个沿分支轴线方向的约束力，上平台共受到7个约束力作用，这7个约束力线性相关，其最大线性无关数为6，限制了上平台所有的自由度，该并联结构有1个冗余约束，属于过约束并联结构。

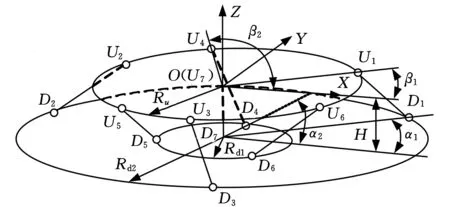
图12　7-SS过约束并联结构示意图

建立7-SS过约束6维力传感器并联结构的刚柔混合模型如图13所示，7个圆柱分支杆具有相同的横截面尺寸，除中间分支外其余6个分支杆长均为l。如图12所示，在上平台中心建立坐标系OXYZ,Ru为上平台球铰点的分布半径,Rd1、Rd2分别为下平台内圈和外圈球铰点的分布半径,H为上下平台间的距离,α1、β1分别表示下、上平台第一个球铰点和坐标原点连线在XY平面内的投影与坐标系X轴的夹角,α2、β2分别表示下、上平台第4个球铰点和坐标原点连线在XY平面内的投影与坐标系X轴的夹角。

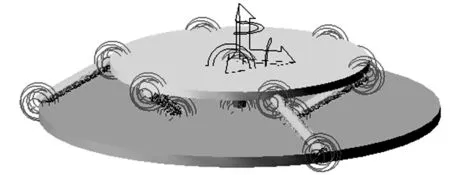
图13　7-SS过约束并联结构的刚柔混合模型

根据文献[18]给定该机构的一组结构参数如表3所示。在坐标系OXYZ下给动平台施加6维外力F=(150 N,200 N,240 N,120 N·m,100 N·m,160 N·m)T,同样地，先按照上文介绍的理论方法[1]得到各分支提供给上平台的约束力的理论值,进而验证仿真结果的正确性。沿各分支轴线方向的约束力FDiUi(i=1,2,…,7)的仿真值与理论值如表4所示。

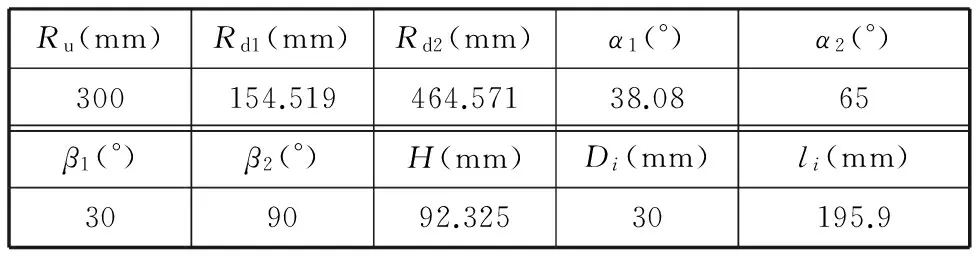
表3　7-SS过约束并联结构的结构参数

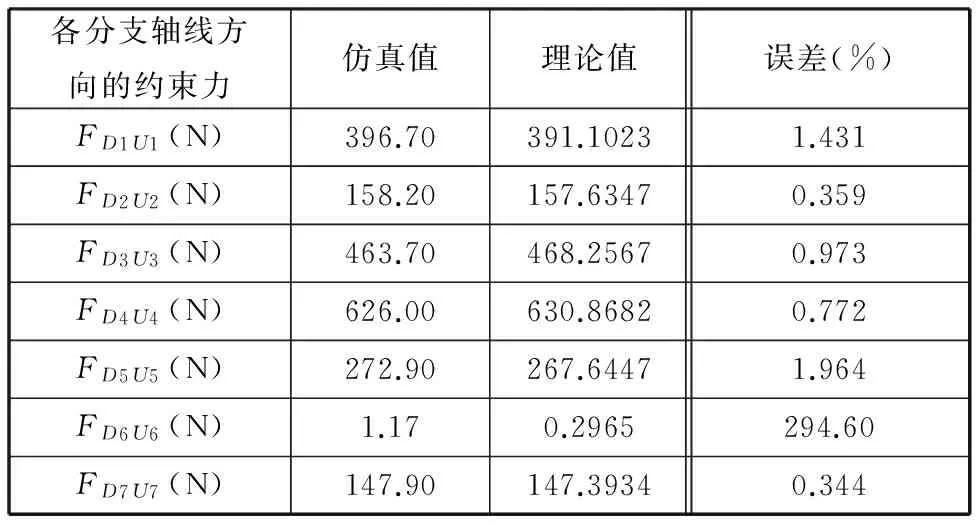
表4　7-SS过约束结构各分支约束力的仿真值与理论值

从表4可以看出,在六维外力F作用下，分支6提供给上平台的约束力与其他分支约束力相比非常小，其仿真值与理论值误差较大,其余分支误差均小于2%。

3.3平面五杆平行四边形机构的受力分析

如图14所示的具有虚约束的平面五杆平行四边形机构也可看作是具有三个分支的并联机构，分支AB、FC、ED均通过转动副连接动平台BD杆和定平台AE杆。在A点建立图13所示的坐标系OXYZ,每个分支提供给BD杆1个过A点垂直于机构平面的约束力、1个X轴方向的约束力偶和1个Y方向的约束力偶。此外，每个分支还提供给BD杆1个沿分支轴线方向的约束力，这3个分支轴线方向的约束力线性相关,最大线性无关数为2，则该机构除具有3个公共约束外还具有1个冗余约束，故平面五杆平行四边形机构也属于过约束并联机构。若驱动加在转动副A处，则分支AB还提供了1个驱动力线矢作用。驱动转矩的大小通过驱动力线矢大小与其之间的关系计算可得。图14中α表示分支AB与定坐标系X轴之间的夹角。

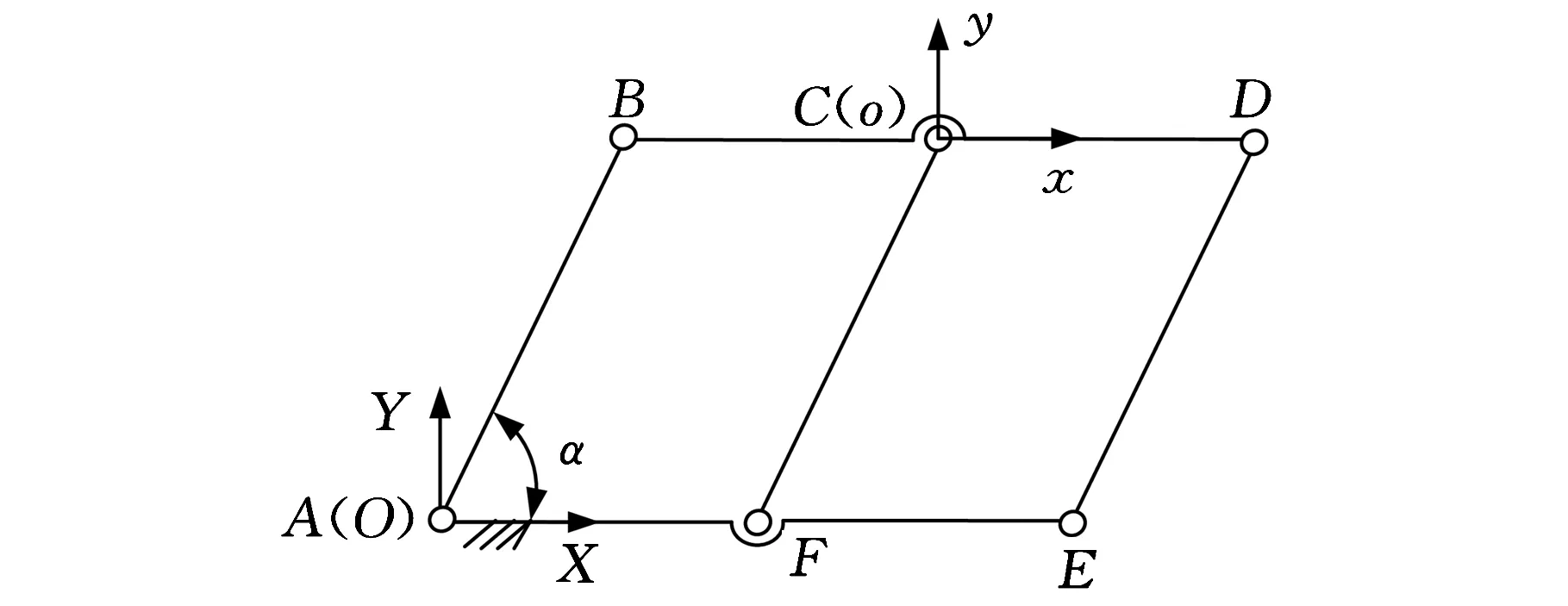
图14　平面五杆平行四边形机构简图

令五根杆具有相同的横截面直径D=0.016 m,三根分支杆长均为l=0.2 m,动定平台等长,长度k=0.36 m,建立该机构的刚柔混合模型如图15所示。

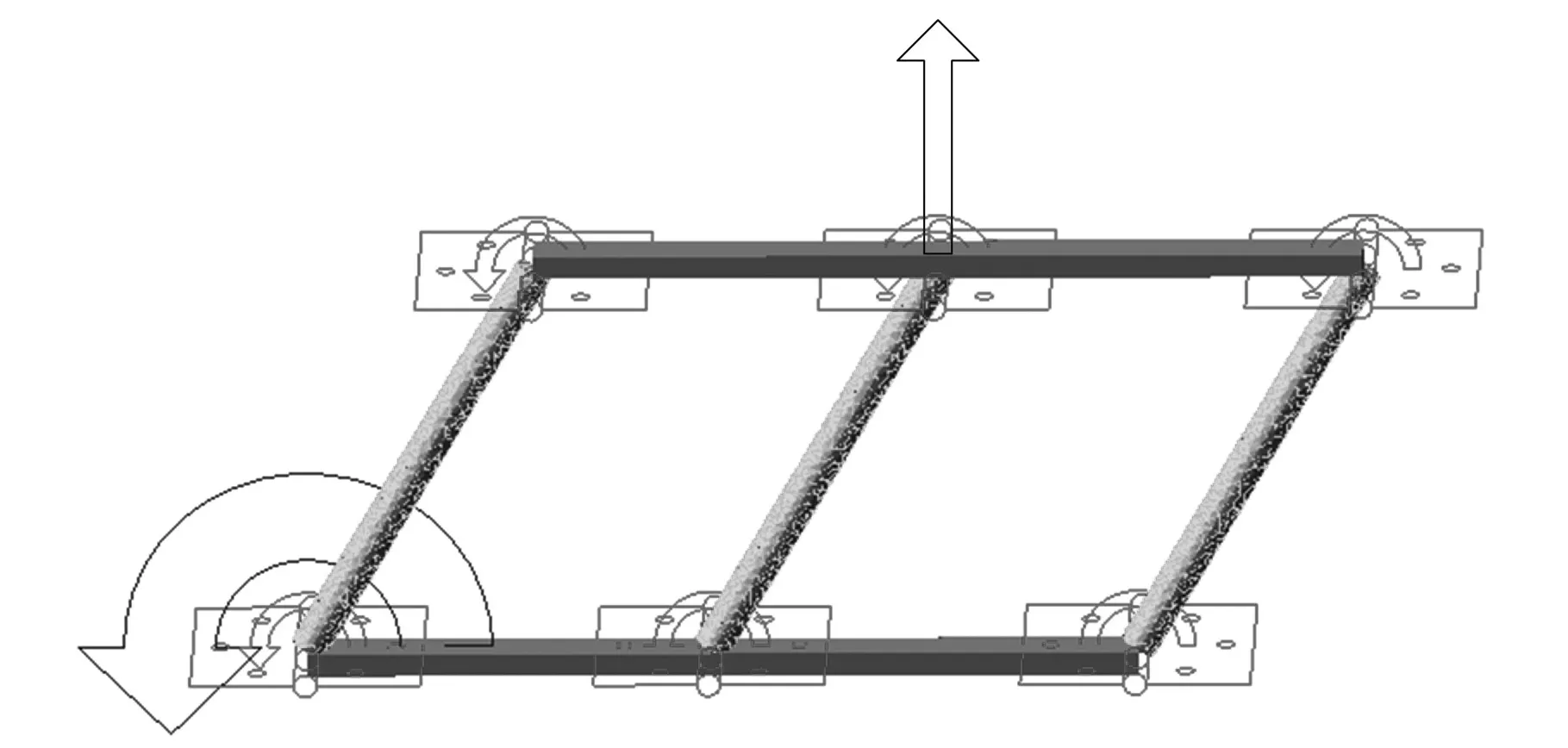
图15　平面五杆平行四边形机构的刚柔混合模型

如图14所示,在BD杆质心建立动坐标系oxyz,动平台受到六维外力时,显然Fx、Fy、Mz方向的外力由该机构3个分支杆轴线方向的约束力和1个驱动力平衡,Fz、Mx、My方向的外力由该机构的3个公共约束平衡，故可分两种情况施加外力对该机构进行受力仿真分析：施加六维外力F=(0 N,0 N,12 N,10 N·m，8 N·m,0 N·m)T并对其进行静力学仿真，分支公共约束的仿真值与理论值如表5所示；施加六维外力F=(10 N，8 N，0 N，0 N·m，0 N·m，5N·m)T并对其进行静力学仿真,分支AB提供的驱动力线矢大小和沿各分支杆轴线方向的约束力的仿真值与理论值如表6所示。

表5　平面五杆平行四边形机构分支

表6　平面五杆平行四边形机构分支杆长方向约束力和

表5和表6的分析结果也表明了本文提出的过约束并联机构受力分析的数值仿真方法的正确性。上述分析结果对应的是该平面机构处于α=60°时的位形受力情况，同理，改变转动副A处的驱动值使机构运动到其他位形，可求解任意位形下该机构的驱动力和各关节约束反力大小。

4　结论

(1)提出了一种过约束并联机构受力的数值仿真分析方法，该方法结合三维建模软件、ANSYS软件和ADAMS软件建立了过约束并联机构的刚柔混合模型，采用虚拟关节代替形状复杂的运动副模型，最终所建模型与理论分析模型完全一致。而且，该方法能够直接驱动模型使机构运动到任意位形对其进行受力分析，不需重建其模型，大大提高了工作效率。

(2)提出的仿真方法建模过程简单，不需要繁琐的理论计算即可快速得到过约束并联机构在任意位形下的驱动力和各关节约束反力大小，为过约束并联机构的受力分析提供了一种便捷途径。

(3)本文提出的方法不仅适用于上述三种类型的过约束并联机构，对其他类型的过约束并联机构也适用，通用性较强。由于该方法未考虑机构各杆件的重力和运动副的变形，后续研究将考虑这些因素。

[1]赵永生,许允斗,姚建涛,等.一种过约束并联机构受力分析的方法[J].中国机械工程,2014,25(6):711-717.

Zhao Yongsheng,Xu Yundou,Yao Jiantao.A Method for Force Analysis of the Overconstrained Parallel Mechanism[J].China Mechanical Engineering,2014,25(6):711-717.

[2]董军,黄清世.具有虚约束的平行四边形机构的受力分析[J].江汉石油学院学报,1991,13(3):64-71.

Dong Jun,Huang Qingshi.Force Analysis of Parallelogram Linkages with Formal Constraints[J].Journal of Jianghan Petroteum Institute,1991,13(3):64-71.

[3]Huang Zhen,Zhao Yan,Liu Jingfang.Kinetostatic Analysis of 4-R(CRR) Parallel Manipulator with Overconstraints Via Reciprocal-screw Theory[J].Advanced Mechanical Engineering,2010:404960.

[4]赵燕,黄真.含过约束力偶的少自由度并联机构的受力分析[J].机械工程学报,2010,46(5):15-21.

Zhao Yan,Huang Zhen.Force Analysis of Lower-mobility Parallel Mechanisms with Over-constrained Couples[J].Journal of Mechanical Engineering,2010,46(5):15-21.

[5]Kerr D R,Griffis M,Sanger D J,et al.Redundant Grasps,Redundant Manipulators,and Their Dual Relationship[J].Journal of Robotics System,1992,9(7):973-1000.

[6]Rocco V,Vincenzo P C.Static and Stiffness Analyses of a Class of Over-constrained Parallel Manipulators with Legs of Type US and UPS[C]//2007 IEEE International Conference on Robotics and Automation.Roma,Italy:IEEE,2007:561-567.

[7]刘胜,李晚龙,杜延春,等.潜器Stewart平台动力学仿真[J].哈尔滨工业大学学报,2009,41(9):249-251.

Liu Sheng,Li Wanlong,Du Yanchun,et al.Dynamic Simulation of Submarine Stewart Platform[J].Journal of Harbin Institute of Technology,2009,41(9):249-251.

[8]王瑞,钟诗胜,王知行.5轴新型数控铣床仿真建模的实现[J].计算机集成制造系统,2005,11(8):1076-1080.

Wang Rui,Zhong Shisheng,Wang Zhixing.Research on 5-DOF NC Milling Machine Simulation Modeling[J].Computer Integrated Manufacturing Systems,2005,11(8):1076-1080.

[9]郝秀清,胡福生, 陈建涛.基于牛顿—欧拉法的3PTT并联机构动力学分析及仿真[J].中国机械工程,2006,17(增刊2):32-36.

Hao Xiuqing,Hu Fusheng,Chen Jiantao.Dynamic Analysis and Simulation to 3PTT Parallel Mechanism Based on New-euler Method[J].China Mechanical Engineering,2006,17(S2):32-36.

[10]徐晓辉,段志善.ADAMS中过约束问题的分析[J].中国科技信息,2008(22):93-95.

Xu Xiaohui,Duan Zhishan.The Analysis of Overconstrained Problem in ADAMS[J].China Science and Technology Information,2008(16):93-95.

[11]陈落根,罗振军,李玉航,等.基于SAMCEF的四自由度并联机器人动力学建模与仿真[J].机械设计与研究,2013,29(6):12-15.

Chen Luogen,Luo Zhenjun,Li Yuhang,et al.The Dynamics Modeling and Simulation for a 4-DOF Parallel Robot Based on SAMCEF Software[J].Machine Design and Research,2013,29(6):12-15.

[12]朱春霞,朱立达, 刘永贤,等.基于虚拟样机技术的并联机床多柔体系统运动学仿真分析[J].机床与液压,2008,36(4):11-13.

Zhu Chunxia,Zhu Lida,Liu Yongxian,et al.Kinematical Simulation of Flexible Multibody System for Parallel Machine Tool Based on Virtual Prototyping[J].Machine Tool & Hydraulics,2008.36(4):11-13.

[13]张建,陈文家,赵兰磊.基于ADAMS的一种风洞试验平台刚柔混合多体建模研究[J].制造业信息化,2011(12):59-62.

Zhang Jian,Chen Wenjia,Zhao Lanlei.Modeling of a New Wind Tunnel Test Bed with Rigid and Flexible Body Based on Virtual Prototyping Technology[J].Manufacturing Informatization,2011(12):59-62.

[14]李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2012.

[15]刘善增,余跃庆,刘庆波,等.3-RRC并联机器人动力学分析[J].机械工程学报,2009,45(5):220-224.

Liu Shanzeng,Yu Yueqing,Liu Qingbo,et al.Dynamic Analysis of 3-RRC Parallel Manipulator[J].Journal of Mechanical Engineering,2009,45(5):220-224.

[16]Joshi S A,Tsai L W.Jacobian Analysis of Limited-DOF Parallel Manipulators[J].ASME Journal Mechanical Design,2002,124(2):254-258.

[17]Xu Yundou,Yao Jiantao,Zhao Yongsheng.Inverse Dynamics and Internal Forces of the Redundantly Actuated Parallel Manipulators[J].Mechanism and Machine Theory,2012,51:172-184.

(编辑王艳丽)

A Numerical Simulation Method for Force Analysis of an Overconstrained PM

Zhao Yongsheng1,2Liu Wenlan1Xu Yundou1,2Yao Jiantao1，2Jin Linru1,3

1.Parallel Robot and Mechatronic System Laboratory of Hebei Province,Yanshan University,Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science of Ministry of National Education,Yanshan University,Qinhuangdao,Hebei,066004 3.BMEIMT Co., Ltd., Beijing,100027

A numerical simulation method for force analysis of the overconstrained PM was proposed,in view of the fact that very few literatures had focused on the force simulation analysis of this type of mechanism at present.The rigid-flexible mixed model of the overconstrained PM was established combining the 3D modeling software,the ADAMS software and ANSYS software,which was idendical with the theoretical one completely.The base,moving platform and kinematic joints were built as rigid bodies,while the links easy to produce spatial composite elastic deformations were built as flexible bodies,and the virtual joints were adopted to replace the actual joints with complex shape during modeling.Only the driving values were needed to be changed to obtain the actuated forces/torques and the reactions of the kinematic joints when the overconstrained PM was in arbitrary configuration,thus avoiding rebuilding the simulation model.Force analyses of three type of overconstrained PMs were carried out using the proposed method.The results show the correctness and universality of the method, meanwhile show that the method provides a simple and effective way for force analysis of the overconstrained PMs instead of complex calculations.

overconstrained parallel mechanism(PM);numerical simulation;force analysis;rigid-flexible mixed model

2014-06-16

国家自然科学基金资助项目(51275439)；国家重点基础研究发展计划(973计划)资助项目(2013CB733000);河北省自然科学基金资助项目(E2014203255)

TH112;TP24 DOI：10.3969/j.issn.1004-132X.2015.12.003

赵永生,男,1962年生。燕山大学副校长,机械工程学院教授、博士研究生导师。主要研究方向为并联机器人理论及其应用、传感器技术。出版专著1部，发表论文120余篇。刘文兰,女,1990年生。燕山大学机械工程学院博士研究生。许允斗(通信作者),男,1985年生。燕山大学机械工程学院讲师。姚建涛，男，1980年生。燕山大学机械工程学院副教授、硕士研究生导师。金林茹，女，1988年生。燕山大学机械工程学院硕士研究生,北京机电院机床有限公司助理工程师。