基于连续蚁群算法的3-RPS并联机构正解
2015-10-29谢志江宋代平
谢志江 梁 欢 宋代平
重庆大学机械传动国家重点实验室,重庆,400030
基于连续蚁群算法的3-RPS并联机构正解
谢志江梁欢宋代平
重庆大学机械传动国家重点实验室,重庆,400030
为了避免传统数值方法求解并联机构正解问题的弊端,提出了一种将并联机构正解问题转化为目标函数优化问题的求解方法。并联机构正解的核心问题是求解一组多元耦合非线性方程组,以此为依据建立了并联机构正解的目标函数优化模型,并提出了一种简单的连续蚁群算法来求解该优化模型。以求解3-RPS并联机构正解为例进行了仿真分析。结果表明,该算法具有良好的全局寻优功能,能够避免初始值和局部极小值对计算结果的影响,不用计算雅可比矩阵及其逆阵,且计算精度满足并联机构正解的要求。
并联机构;运动学正解;蚁群算法;多目标优化
0 引言
并联机构坐标测量机以其测量误差小、测头位置灵活、成本较低等优点,成为坐标测量机领域研究的新热点[1]。该测量机测量模型的原理从本质上来说是并联机构位置正解,因此一种高效、精确的并联机构正解算法对提高并联机构坐标测量机测量精度是非常重要的。
并联机构位置正解的核心问题一般归结为求解一组多元耦合的非线性方程组。传统算法分解析法和数值法[2]两种。解析法主要是通过消元法得到单独参数多项式,然后再求解。这种方法不需要设置初始值,并且能够求得全部解,避免位置奇异问题。程世利等[3]提出了一种6-SPS并联机构运动学正解的解析方法。但是,该方法推导过程复杂,不具有通用性,一种解析方法仅求解一种模型。数值法主要是通过Newton法或Newton-Raphson法迭代求解[4-5],该方法需要设置初始值并且每次迭代都需要计算雅可比矩阵及其逆阵,因此该类方法计算速度较慢且计算精度受初始值的影响较大。韩方元等[6]提出了一种3-RPS并联机构正解的快速数值算法,该算法迭代过程中不需要计算雅可比矩阵及其逆阵,但对机构的结构具有一定的依赖性,通用性较差。
本文先将非线性方程组转化成多目标优化问题,再根据权和法将多目标优化转化成单目标优化,最后采用连续蚁群算法进行求解。
1 并联机构逆解分析
图1为三坐标测量机3-RPS并联机构的机构简图,该机构由底部定平台、顶部动平台以及三条支链构成,各支链在平台上均匀分布且从下向上依次为转动副(R)、移动副(P)、球副(S)。通过驱动移动副,改变三条支链的长度来实现动平台的运动,该并联机构具有三个自由度,即绕x轴、y轴的转动以及沿z轴的移动。

图1 3-RPS并联机构简图
如图1所示,在底部定平台几何中心建立定坐标系Oxyz,x轴过A1点,y轴与A3A2平行,z轴方向垂直定平台向上。在顶部动平台几何中心建立动坐标系O1x1y1z1,x1轴过B1点,y1轴与B3B2平行,z1轴方向垂直动平台向上。上下平台半径分别为rb和Ra,ai表示Ai点在定坐标系Oxyz的矢量,bi表示Bi点在动坐标系O1x1y1z1的矢量,p表示O1点在定坐标系Oxyz的矢量,坐标为(x,y,z),li表示第i条支链的长度,ni表示各支链方向的单位向量。则有
ai=Ra(cosθi,sinθi,0)T
bi=rb(cosθi,sinθi,0)T
由图2封闭矢量图可得
lini=Rbi+p-ai
(1)
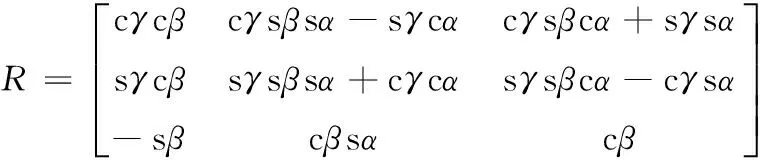
其中,R表示动坐标系O1x1y1z1相对于定坐标系Oxyz的旋转变换矩阵,α、β、γ分别为Z-Y-X型的欧拉角,c代表cos,s代表sin。

图2 封闭矢量图
各条支链受转动副的约束,只能在三个垂直平面内运动,可得
Rbi·ui=0
(2)
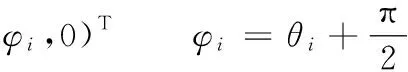
式中,ui为各转动副轴线方向的单位向量。
由式(2)可得
(3)
将式(3)代入式(1)可得各支链长li为
(4)
则机构的逆解可以记为
li=fi(α,β,z)
(5)
2 机构正解的目标优化模型
机构正解的本质是求解一组非线性方程组,由式(4)可得该方程组:
i=1,2,3
(6)
将该非线性方程组转化成多目标优化问题,即求解式(7)的最小值:
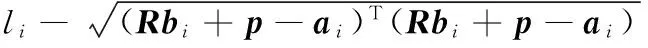
(7)
权和法可以将多目标优化问题转化为所有目标的加权和的标量问题,即:
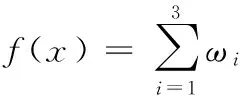
(8)
式中,ωi为权重系数。
将式(7)代入到式(8)中,可得机构正解数学优化模型:

(9)
由于要求式(6)为零,所有各子目标函数权重系数相等,为计算简便,故取ωi=1。
3 连续蚁群算法
蚁群算法是一个求解离散问题的数学模型[7]。而目标函数的优化是一个连续域的优化问题,因此需要一种适用于连续域内的蚁群算法。一种简单的方式是在目标函数可行域打网格,将连续空间离散化,再使用蚁群算法进行求解[8],该方法存在求解精度不高,搜索空间大等缺点。Dero等[9]提出了一种适用于连续域内的蚁群算法,该方法采用信息素的传递以及直接交流两种方式结合来指导蚁群的寻优;文献[10-12]也提出了几种适用于连续域内的蚁群算法。在前人的基础上,本文提出一种较为简单的连续蚁群算法。
该连续蚁群算法的基本思路如下:
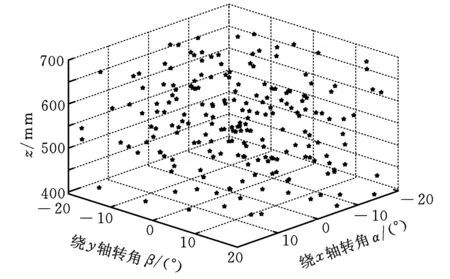
首先根据三坐标测量机3-RPS并联机构的空间运动范围设定机构各自由度取值范围:αl<α<αu,βl<β<βu,zl (1)在各变量的可行域αl<α<αu,βl<β<βu,zl (2)根据目标函数确定信息素的大小,信息素的表达式为 τ=-f(α,β,z) (10) 其增减性与目标函数相反,本文求目标函数最小值,即信息素的最大值。因为f(α,β,z)正向无限趋近0时,其信息素值负向无限趋近于0,从而不便于衡量信息素的浓度,故同时也用式(11)平均信息素值进行衡量: τmean=mean(-f(α,β,z)) (11) 式中,mean()为取平均值函数。 (3)由式(10)确定蚁群初始位置时信息素值的大小,从中记录最优值τbest并计算平均信息素值τmean的大小。 (4)蚁群转移概率决定了蚁群进行全局搜索还是局部搜索,表达式为 (12) 其中,i表示第i次蚁群移动,j表示第j只蚂蚁,τi,j表示第i次蚁群移动后第j只蚂蚁所对应的信息素值。 (6)蚁群移动完成一次,对每只蚂蚁的信息素值进行更新,如下式所示: (13) 式中,ρ为信息素残留系数。 (7)如此反复迭代,当迭代次数n小于规定最大循环次数,转至步骤(4),否则跳出循环,输出最终解。 图1所示3-RPS并联机构的参数如下:定平台半径Ra=257 mm,动平台半径rb=141 mm,机构各自由度运动范围为:α,β∈[-20°,20°],z∈[395,695]mm。 本文以求解当α= 15°,β=10°,z=495 mm位置时的正解为例,验证连续蚁群算法在求解并联机构正解的有效性。其他位置求解结果如表1所示。而采用传统Newton-Raphson法对该位置求解,结果如表2所示。 表1 连续蚁群算法计算结果 表2 Newton-Raphson法计算结果 由3-RPS逆解求得三条支链长度分别为:l1=485.3 mm,l2=553.5 mm,l3=490.3 mm。可得目标函f(α,β,z)在空间可行域内的值域,如图3所示。 图3 目标函数f(α,β,z)的值域 正解问题可以转化为寻找该立方体中的最小值,将蚁群随机分布在如图3所示区域中,为了观察方便,将立方体图剖开,并将颜色淡化,如图4所示。 图4 蚂蚁初始位置分布图 采用连续蚁群算法进行计算,所有蚂蚁聚集在目标函数f(α,β,z)的最小值处,不受局部最小值的影响,如图5、图6所示。 图5 蚂蚁运动300次位置分布图 图6 蚂蚁运动600次位置分布图 该算法的收敛速度可从信息素以及平均信息素值的变化看出,如图7所示。 图7 最大信息素值和平均信息素值 由以上计算可得,当目标函数f(α,β,z)取最小值时,α=15.0020°,β=10.0016°,z=495.0071 mm,f(α,β,z)=-2.25×10-4,计算精度满足要求。 从以上仿真分析中可以看出,采用Newton-Raphson法计算的结果直接受初始值的影响,不同的初始值计算结果偏差很大;而采用本文提出的连续蚁群算法,可以避免初始值对计算结果的影响,得到精确解。 本文通过将求解并联机构正解的非线性方程组转化成目标函数的最优化问题,采用连续蚁群算法进行求解,避免了初始值的选取对计算精度的影响。不需要求解雅可比矩阵及其逆阵,计算过程简便快捷。采用全局搜索和局部搜索相结合的方法,计算结果不受局部极小值的影响。该方法适用于求解所有并联机构正解问题,具有良好的通用性。 [1]胡鹏浩,李松原.3-PSS并联机构正解及其在坐标测量机中的应用[J].光学精密工程,2012,20(4):782-788. Hu Penghao,Li Songyuan.Kinematic Solution of 3-PSS Parallel Mechanism and Its Application in Parallel CMM[J].Optics and Precision Engineering,2012,20(4):782-788. [2]季晔,刘宏昭,原大宁.并联机构位置正解方法研究[J].西安理工大学学报,2010,26(3):277-281. Ji Ye,Liu Hongzhao,Yuan Daning Research on Approach of Forward Positional Analysis of Parallel Mechanism[J].Xi’an University of Technology Newspaper,2010,26(3):277-281. [3]程世利,吴洪涛,姚裕.6-SPS并联机构运动学正解的一种解析化方法[J]. 机械工程学报,2010,46(9):26-31. Cheng Shili,Wu Hongtao,Yao Yu.An Analytical Method for the Forward Kinematics Analysis of 6-SPS Parallel Mechanisms[J].Chinese Journal of Mechanical Engineering,2010,46(9):26-31. [4]Lee K,Shah K D.Kinematic Analysis of a Three Degrees of Freedom in-parallel Actuated Manipulator[J].IEEE Journal of Robotics and Automation,1988,4(3):361-367. [5]Hashimoto M,Imamura Y.Kinematic Analysis and Design of a 3 DOF Parallel Mechanism for a Passive Compliant Wrist of Manipulators[J].Transactions of the Japan Society of Mechanical Engineers,1998,64:2116-2123. [6]韩方元,赵丁选,李天宇.3-RPS并联机构正解快速数值算法[J].农业机械学报,2011,42(4):229-233. Han Fangyuan,Zhao Dingxuan,Li Tianyu.A Fast Forward Algorithm for 3- RPS Parallel Mechanism[J].Transactions of the Chinese Society of Agricultural Machinery,2011,42(4):229-233. [7]申铉京,刘阳阳,黄永平.求解TSP问题的快速蚁群算法[J].吉林大学学报,2013,43(1):147-151. She Xuanjing,Liu Yangyang,Huang Yongping.Fast Ant Colony Algorithm for Solving Traveling Salesman Problem.Journal of Jilin University,2013,43(1):147-151. [8]高尚,杨静宇.群智能算法及其应用[M].北京:中国水利水电出版社,2006. [9]Dero J,Siam P.Continuous Interacting Ant Colony Algorithm Based on Dense Heterarchy[J].Future Generation Computer Systems,2004,5(20):841-856.[10]Li Y J,Wu T J.An Adaptive Ant Colony System Algorithm for Continuous Space Optimization Problems[J].Journal of Zhejiang University:Science,2003,4(1):40-46. [11]Karaboga N,Kalinli A,Karaboga D.Designing Digital IIR Filters Using Ant Colony Optimization Algorithm[J].Engineering Application of Artificial Intelligence,2004,17(2):301-309. [12]Socha K,Dorigo M.Antcolony Optimization for Continuous Domains[J].European Journal of Operational Research,2008,185(3):1155-1173. (编辑袁兴玲) Forward Kinematics of 3-RPS Parallel Mechanism Based on a Continuous Ant Colony Algorithm Xie ZhijiangLiang HuanSong Daiping The State Key Laboratory of Mechanical Transmission,Chongqing University,Chongqing,400030 In order to avoid the drawbacks of traditional numerical methods for solving the problem of parallel mechanism forward kinematics,this paper proposed a method that translated the problem of solving parallel mechanism forward kinematics into objective function optimization problems. The central issue of solving the problem of parallel mechanism forward kinematics was to solve a set of multiple coupled nonlinear equations,thus objective function optimization model of parallel mechanism forward kinematics was established,and a kind of simple continuous ant colony algorithm was put forward to solve the above optimization model.Taking the 3-RPS parallel mechanism for example,some simulation analyses were completed.The results show that the algorithm has a good global optimization function and can avoid initial values and the local minimum effect on the calculation results without calculating Jacobian matrix and its inverse matrix.The accuracy of calculation meets the requirements of parallel mechanism of forward kinematics. parallel mechanism;forward kinematics;ant colony algorithm;multi-objective optimization 2014-03-10 国家自然科学基金资助项目(51105392);重庆市自然科学基金资助项目(cstc2011jjA70006);中央高校基本科研业务费专项资金资助项目(CDJRC10110005) TP391.9;TH112DOI:10.3969/j.issn.1004-132X.2015.06.017 谢志江,男,1963年生。重庆大学机械传动国家重点实验室教授、博士研究生导师。主要研究方向为机械创新设计。梁欢,男,1988年生。重庆大学机械传动国家重点实验室硕士研究生。宋代平,男,1979年生。重庆大学机械工程学院副教授。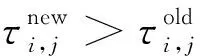

4 求解机构正解实例






5 结束语
