通用量子门神经网络在齿轮故障诊断中的应用

李　胜　张培林　李　兵　王国德

1.军械工程学院,石家庄,050003　　2.武汉军械士官学校,武汉,430075

通用量子门神经网络在齿轮故障诊断中的应用

李胜1张培林1李兵1王国德2

1.军械工程学院,石家庄,0500032.武汉军械士官学校,武汉,430075

为进一步提高齿轮故障诊断能力,结合目前神经网络机理的研究进展,建立了一种基于通用量子门的量子神经元模型,提出了通用量子门神经网络(universal quantum gate neural network,UQGN)算法。首先,该算法将转换后的量子态训练样本作为输入。然后,利用量子旋转门和通用量子门完成旋转、选择、翻转和聚合等一系列操作，并完成网络参数的更新。最后，将训练后的结果输出。在数学上，证明了UQGN算法的泛化能力。利用该算法对齿轮的正常、齿面磨损、齿根裂纹和断齿4种情况进行了模式识别。实验结果表明，与普通神经网络和普通量子神经网络相比，UQGN算法在泛化性能、鲁棒性、准确率和执行时间等方面具有较好的效果。

量子计算;通用量子门;量子神经网络;齿轮;故障诊断

0　引言

目前,应用于齿轮故障诊断中的模式识别方法主要有小波变换、神经网络、支持向量机等。量子计算具有量子干涉和量子纠缠等特性,与经典计算相比,它可以极大地提高运算速度和缩小存储空间[1]。由于量子神经网络(quantum neural network,QNN)具有提高神经网络的逼近能力和信息处理效率的优点,被广泛应用在模式识别、函数逼近、优化PID控制参数等方面[2-4]。在齿轮故障诊断方面,文献[5-6]对齿轮箱故障信号进行量子特征提取,并采用量子神经网络进行故障诊断,取得了不错的效果。

目前,量子神经网络的研究主要体现为以传统神经网络的结构,引入量子理论的概念,建立量子神经网络模型。根据文献[7]的研究结果,本文提出了一种基于通用量子门的量子神经网络学习算法。该算法建立了一种新的量子神经元模型,并采用Levenberg-Marquardt(LM)法确定了旋转角度的大小和方向。运用本文方法对齿轮的正常、齿面磨损、齿根裂纹和断齿的故障信号进行了模式识别,实验结果表明,与普通神经网络CNN和普通量子神经网络CQN相比,通用量子门神经网络(universal quantum gate neural network,UQGN)在泛化性能、鲁棒性、准确率和执行时间等方面具有明显的优势。

1　通用量子门神经网络

1.1通用量子门神经元模型

U=Φ(δ)Rz(α)Ry(θ)Rz(β)

(1)

其中,α、β、δ、θ为实参数。

本文的通用门量子门神经元主要由输入、旋转、选择、翻转、聚合、输出等操作组成。图1为通用量子门神经元模型。

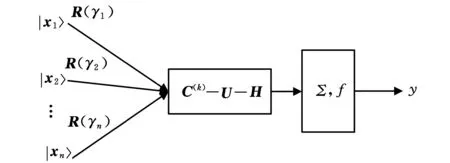
图1　通用量子门神经元模型

图1中,输入为量子位|X〉=[|x1〉|x2〉…|xn〉],R(γn)用于量子相位的旋转操作,通用量子门C(k)-U-H用于选择和翻转操作,C(k)为第k次的受控非门，H为Hadamard门,Σ为求和算子,f为目标函数，y为量子位处于|1〉的概率幅输出。

设|xi〉=[cosφisinφi]T,则

R(γi)|xi〉=[cos(φi+γi)sin(φi+γi)]T

(2)

HUCR(γi)|xi〉=

(3)

在图1中,通用量子门神经元的输入输出关系为

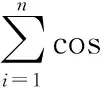
(4)

1.2通用量子门神经网络模型

图2　三层通用量子门神经网络模型

本文提出的通用量子门神经网络是按照一定的拓扑结构将若干个通用量子门神经元连接组合而成的。本文采用三层神经网络,即输入层、隐含层和输出层，图2描述了本文的神经网络模型。其中,输入层、隐含层和输出层分别有n、p和m个神经元。图2中各参数代表的意义为:|xi〉为网络输入,ym为网络输出,R(γi j)为输入层和隐含层之间的连接权值,|φj k〉为隐含层和输出层之间的连接权值。H和C(p)-U分别为输入层和隐含层的传递函数。通用量子门神经网络模型的输入输出关系为

hj=UCR(γi j)H|xi〉=

(5)

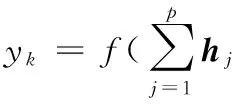
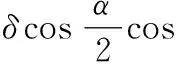
(6)

i=1,2,…,n;k=1,2,…,m

1.3样本的量子态描述

已知在没有湍流的情况下，距离出射平面L处的场强可以通过Huygens-Fresnel积分得到输出场强表达式.在真空中传输L距离后的场强UL(r,θ,L) 表示为[15]

由于训练样本集初始状态为实数值，应相应地转换为神经网络模型的量子态输入,即X=[x1x2…xn]T⟹|X〉=[|x1〉|x2〉…|xn〉]T转换公式为

|xi〉=cosφi|0〉+sinφi|1〉=[cosφisinφi]T

(7)

1.4模型参数的更新规则

在通用量子门神经网络模型中,共有6组参数,其中,α、β、δ、θ为给定实数值。参数γi j和φj k采用LM法进行更新。

定义神经网络的性能指数为

(8)

根据LM方法,γi j和φj k的更新公式为

Δγi j=(JT(γi j)J(γi j)+λ1I)-1JT(γi j)e(γi j)

(9)

Δφj k=(JT(φj k)J(φj k)+λ2I)-1JT(φj k)e(φj k)

(10)

其中,λ1和λ2为0.01;J(γi j)和J(φj k)为雅可比矩阵：

(11)

(12)

与普通量子门神经网络相比,通用量子门神经网络主要有以下优势：①采用通用量子门可以进行任意的幺正变换，能将运算速度提高，便于实施程序编译。②采用LM方法而不是梯度下降法进行参数更新，可以提高参数的收敛速度，防止陷入局部极小点。③神经网络模型中的连接权值全部采用量子态描述，达到运算的一致性。

2　通用量子门神经网络泛化性能分析

在量子计算过程中,一系列量子门的操作会造成一些误差。假设误差是幺正的,设为on。幺正误差越小,所导致的泛化误差越小,从而神经网络的性能也就越好。在通用量子门神经网络模型中,幺正误差on为

(13)

定理若x∈Cn,y∈Cm,对∀ε>0,∃σ>0,当|on|<σ,则E<ε。

证明对∃σ>0有：

则神经网络模型的泛化误差为

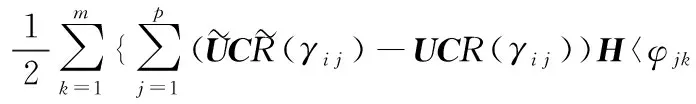
设mσ2/2=ε,由于ε>0,σ>0,因此,E

3　齿轮故障诊断及结果分析

采用本文算法进行模式识别,进一步验证模型的有效性和泛化性，并与普通神经网络和普通量子神经网络进行对比分析。

3.1齿轮故障信号的采集和特征提取

齿轮的故障振动信号采集于一个二级传动齿轮箱，传感器型号为CA-YD-185,将传感器安装在齿轮箱的轴承座上。对齿轮的正常、齿面磨损、齿根裂纹和断齿等4种状态进行信号采集。设定齿轮转速为600r/min,采样点数为2048,采样频率为12 800Hz。齿轮的时域波形图见图3。对每一种状态共采集50个样本，其中，选取15个作为训练样本，其余35个作为测试样本。

图3　齿轮4种状态下的时域波形图

由图3可以看出,在时域上,4种工作状态的振动信号之间有很明显的差异。齿面磨损时，噪声稍有加强;齿根裂纹时,在裂纹处有较强的信号;断齿时,噪声明显,且断齿处的振动信号变强。

齿轮的故障特征集是由时域信号的10个统计参数组成的，这10个统计参数分别为峰峰值、均方值、方差、方根幅值、均方幅值、峭度、波形指标、峰值指标、脉冲指标、边界指标。因此,共得到40个特征参数。同时，对提取出的特征参数集进行归一化处理，以降低特征参数间的差异性。归一化公式为

(14)

3.2齿轮故障信号的模式识别

为了便于比较普通神经网络、普通量子神经网络和通用量子门神经网络的性能，将三个神经网络的结构统一设定为10-25-4,迭代步数t为1000，限定误差为0.05。其中，通用量子门神经网络的参数设置如下：γi j和φj k的初始值为0.01π,α=θ=0.25π,β=0.1π,δ=0.125π。普通神经网络和普通量子神经网络的参数设置如下：学习速率为0.9。

(1)迭代步数与泛化误差。图4所示为三种算法迭代步数与泛化误差的关系。由图4可见，当迭代步数不断增加时，这三种神经网络模型的泛化误差会不断地减小。其中，UQGN在迭代步数为447时，泛化误差达到0.049并保持稳定;CQN在迭代步数为686时,泛化误差达到0.051并保持稳定;CNN在迭代步数为810时,泛化误差达到0.084并保持稳定。这样可以说明,UQGN算法的迭代步数远远小于CQN和CNN的迭代步数，并且算法的泛化误差更小,因此,UQGN具有很好的泛化性和鲁棒性。

图4　迭代步数与泛化误差的关系

图5　迭代步数与分类准确率的关系

(2)迭代步数与分类准确率。图5所示为三种算法迭代步数与分类准确率关系的对比结果。由图5可以看出,随着迭代步数的增加,分类准确率也跟着提高。UQGN算法在迭代步数为570时,分类准确率达到98.5%;CQN算法在迭代步数为750时，分类准确率达到95.4%;CNN算法在迭代步数为860时,分类准确率达到91.2%。通过对比发现,相比于CNN和CQN算法,UQGN算法的收敛性更好,收敛速度快,并且分类准确率较高。

(3)准确率统计和执行时间。利用UQGN、CQN和CNN算法分别进行20次独立训练。表1所示为算法的结果。由表1可以看出,UQGN的最大准确率达到了99.1%,比CQN和CNN算法的准确率要高,同时,UQGN算法的执行时间也缩短了很多。因此,UQGN算法具有较高的分类准确率和较短的执行时间。

表1　三种算法的结果

综上所述,通用量子门神经网络在泛化性能、鲁棒性、准确率和执行时间上具有明显好于普通神经网络和普通量子神经网络的优势。

[1]李士勇，李盼池. 量子计算与量子优化算法[M]. 哈尔滨：哈尔滨工业大学出版社，2009.

[2]李飞,赵生妹,郑宝玉.量子神经网络及其在CDMA多用户检测中的应用[J].信号处理,2005,21(6):555-559.

Li Fei,Zhao Shengmei,Zheng Baoyu.Quantum Neural Networks and Its Application in CDMA Multiuser Detection[J].Signal Processing,2005,21(6):555-559.

[3]熊和金，桂启发. 量子神经网络动力学及其在信息安全中的应用[J].浙江万里学院学报,2003,16(2):10-13.

Xiong Jinhe,Gui Qifa.Dynamics of Quantum Neural Networks and Its Applications to Information Security[J].Journal of Zhejiang Wanli University,2003,16(2):10-13.

[4]于瓅,汪家权.改进的QGA-BP模型在复杂水质预测中的应用[J].模式识别与人工智能,2012,25(4):705-708.

Yu Li,Wang Jiaquan.Application Research on Complex Water Quality Prediction with Improved QGA-BP Model[J].Pattern Recognition and Artificial Intelligence,2012,25(4):705-708.

[5]崔晓静.基于量子特征与ICA技术的齿轮箱故障诊断研究[D].沈阳:中北大学,2011.

[6]李悦.量子ICA技术在故障诊断中的应用研究[D].沈阳:中北大学,2012.

[7]Quiroga R Q,Fired I,Koch C.Brain Cells for Grandmother[J].Scientific American,2013,308(2):30-35.

[8]Benenti G,Casati G,Strini G.Principle of Quantum Computation and Information I[M].Singapore:World Scientific,2007.

(编辑袁兴玲)

Application of Universal Quantum Gate Neural Network in Gear Fault Diagnosis

Li Sheng1Zhang Peilin1Li Bing1Wang Guode2

1.Ordnance Engineering College,Shijiazhuang,050003 2.Wuhan Ordnance Non-Commissioned Officer Academy,Wuhan,430075

In order to improve the ability of gear fault diagnosis,considering the current research of neural network mechanism,a quantum neuron model was proposed based on universal quantum gate and an universal quantum gate neural network(UQGN) was established.Firstly,the input was quantum training samples after transformed.Then,quantum rotation gate and an universal quantum gate were used for rotation selection overturn and aggregation,and the network parameters were updated.Finally,the trained results were as output.The generalization performance of UQGN was proved in mathematics.The proposed method was applied to pattern recognition of gear fault conditions.The experimental results indicate that, compared with common neural network and common quantum neural network,UQGN has better effects on generalization performance, robustness accuracy and execution time.

quantum computation;universal quantum gate;quantum neural network;gear;fault diagnosis

2014-02-04

国家自然科学基金资助项目(E51205405)

TP18DOI：10.3969/j.issn.1004-132X.2015.06.012

李胜, 男, 1986年生。 军械工程学院七系车辆工程教研室博士研究生。主要研究方向为量子优化与智能识别算法，已发表12篇论文。张培林，男，1955年生。军械工程学院七系车辆工程教研室教授、博士研究生导师。李兵，男，1982年生。军械工程学院四系中程导弹教研室博士、副教授。王国德，男，1986年生。武汉军械士官学校高炮教研室讲师。