基于网格支配的微型多目标遗传算法
2015-10-29符纯明刘桂萍邓善良
符纯明 姜 潮 刘桂萍 邓善良
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
基于网格支配的微型多目标遗传算法
符纯明姜潮刘桂萍邓善良
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
提出了一种基于网格支配的微型多目标遗传算法,该算法在求解较多目标函数的优化问题时具有较好的收敛性和较高的计算效率。该算法引入网格支配概念并结合微型多目标遗传算法,在每一代进化种群中计算各个个体的网格值、网格拥挤距离和网格坐标点距离,根据网格支配分级和网格选择机制策略选取精英个体,并对其进行交叉和变异操作,使其朝前沿面收敛以获得Pareto最优解。4个测试函数和2个工程实例验证了该算法的有效性。
多目标遗传算法;网格支配;微型种群; Pareto最优解;耐撞性
0 引言
在实际工程设计中,经常遇到多目标优化问题(multi-objective optimization problem,MOP),如汽车正面碰撞的结构优化设计中,轻量化与最大吸能为两目标优化问题,两者难以同时达到最优,只能获得一组无法进行简单比较的Pareto解。多目标遗传算法可在无需考虑目标函数和约束函数满足连续性和可导性的条件下,对线性或者非线性目标函数进行有效求解,因而引起了众多学者的关注,并被广泛应用于求解实际工程问题[1-3]。Schaffer[4]1985年提出了向量评估遗传算法(vector evaluated genetic algorithm,VEGA),用于解决机器学习的多目标问题。随后,一系列的多目标遗传算法被提出和发展,其中以Deb等[5]的NSGA-Ⅱ(non-dominated sorting GA-Ⅱ)算法和Zitzler等[6]的SPEA2(strength Pareto EA2)算法应用最为广泛。在汽车碰撞安全性设计中,谢然等[7]将NSGA-Ⅱ算法用于40%的偏置正面碰撞中,在满足6σ可靠性、扭转刚度和质量要求的约束条件下,提高了整车的碰撞安全性能。为提高计算效率,刘桂萍等[8-10]将微型遗传算法(micro genetic algorithm,μGA)[11]引入多目标优化问题中,提出了微型多目标遗传算法(micro multi-objective GA,μMOGA),该算法在计算效率、解的均匀性和工程实用性等方面具有较好的综合性能。Yang等[12]提出了基于网格支配的进化算法(grid-based evolutionary algorithm,GrEA),利用网格能同时反映收敛性和多样性的特点,使得个体朝着Pareto最优解方向迭代。
本文在微型多目标遗传算法μMOGA的基础上结合网格支配的概念,提出了一种具有网格属性的多目标遗传算法Gr-μMOGA(μMOGA based on grid domination),与现有方法相比,该算法在求解较多目标函数问题时具有较好的收敛性和均匀性,并提高了计算效率。
1 多目标优化相关概念
多目标优化广泛存在于实际工程中,其优化目标函数之间可能不一致甚至相互冲突,因此难以获得一个类似于单目标的最优解,而只能获得一组无法进行简单比较的Pareto最优解。一般的MOP被定义为[13]
(1)
式中,fk(x)、gi(x)和hj(x)分别为目标函数、不等式约束函数和等式约束函数;m、p和q分别为目标函数、不等式约束和等式约束函数的个数;x、xL和xU分别为优化变量、优化变量的下界和上界。

∀i∈(1,2,…,m):fi(x)≤fi(y)且
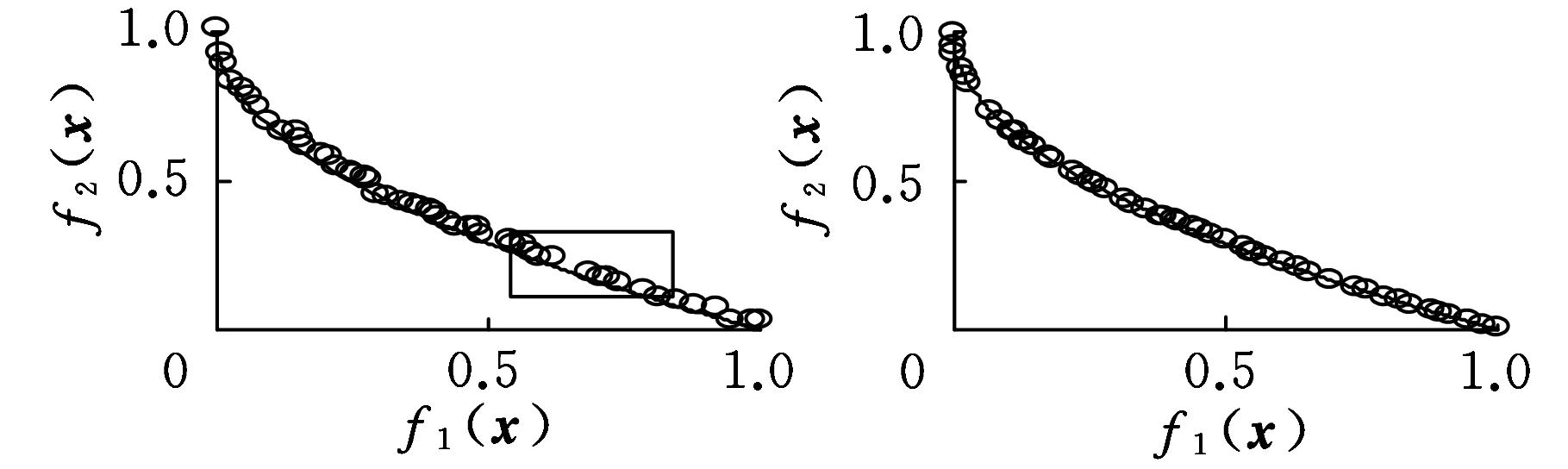
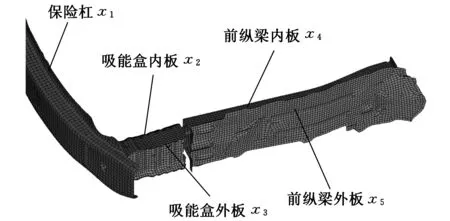
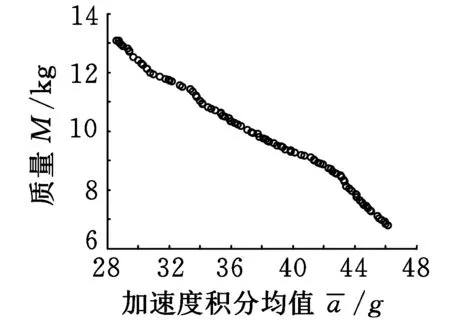
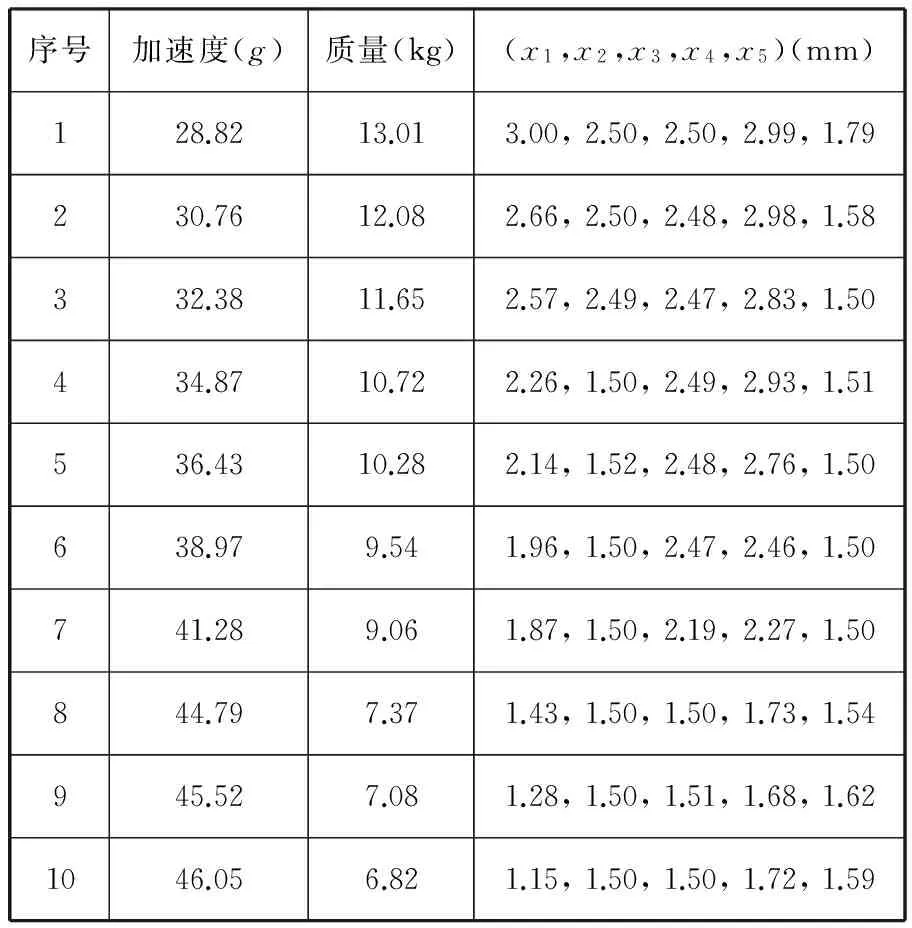
∃j∈(1,2,…,m):fj(x) 现有的多目标优化方法大都是针对二维目标函数问题,而对于较多目标函数问题通常难以获得较好的Pareto解。为此,本文构建一种新的基于网格支配的微型多目标遗传算法Gr-μMOGA,用于求解较多目标函数的一类实际工程多目标设计问题。网格支配在文献[12,14]被提出,通过该方法可保证较多目标函数下Pareto解集的计算精度;μMOGA算法由刘桂萍等[9]提出,通过小种群和重启动策略可有效保证多目标优化的计算效率。本文提出的Gr-μMOGA算法在求解较多目标函数问题时,将兼具精度和效率的双重优点。 2.1网格的概念及相关参数定义 第k个目标函数的网格间距dk为 则个体x在第k个目标函数空间的网格值Gk(x)为 (2) 其中,floor(·)表示最小取整函数,fk(x)为个体x在第k个目标函数的真实函数值。由式(2)知,图1中5个个体在第k个目标函数下的网格值Gk(x)从左到右分别为0、1、3、3和4。 图1 第k个目标函数赋予的网格属性 个体x在m个目标函数下的网格值之和为 (3) ∀i∈(1,2,…,m):Gi(x)≤Gi(y)且 ∃j∈(1,2,…,m):Gj(x) 个体x和y在m个目标函数下的网格值之差定义为网格差值,记为GD: (4) 当个体y满足N(x)={y|GD(x,y) (5) Gr值和dGC值能较好地度量解的收敛性和多样性,但当两者值相等时则无法区分个体,故引入网格坐标点距离,记为dGCP: (6) 式中,dGCP为个体x在超方体中与理想点(超方体中所有目标函数值最小的点)的正则化欧拉距离。 通过Gr、dGC和dGCP值的比较与选择获得精英个体。以两目标函数为例,6个个体在网格中的Gr值和dGC值分别如图2所示。如个体C在网格中的Gr值和dGC值计算式为:Gr(C)=3+3=6,dGC(C)=(2-1)+(2-1)=2。 图2 个体在网格中的Gr值和dGC值 2.2算法流程 以NSGA-Ⅱ算法和SPEA2算法为代表的多目标进化算法通常采用大种群计算,计算量大,效率较低。Gr-μMOGA算法采用小种群[9](5~8个个体)结合重启动策略,并基于网格支配进行迭代进化,能提高效率并满足解的收敛性要求,其计算流程如图3所示。 图3 Gr-μMOGA计算流程 (1)在可行域空间产生5~8个个体形成初始种群P1。设外部种群Pe大小为N,外部种群出现相同的连续代数的次数记为if lag。 (2)网格支配分级。将外部种群Pe和进化种群Pt合并成Rt,将Rt进行网格支配分级(R1,…,Rm)。若Pe=R1,则if lag+1。 (3)当if lag大于设定值M(一般取值为2~9)时,则采用重启动策略。重新在可行域空间中产生进化种群Pt,并加入Rt中进行网格支配分级,否则进行网格选择机制。 (4)网格选择机制。当|Pt+1|+|Ri| (5)当进化代数大于设定的n值时终止进化,并输出外部种群个体,否则转(6)继续进化。 (6)遗传操作。选择外部种群的精英个体进行交叉、变异等操作,从而生成子代种群Pt+1,转(2)进行迭代进化。 该算法采用小种群计算效率高的优点并结合重启动策略,避免了早熟收敛的特点,能有效地求解较多目标优化问题。 3.1两目标测试函数 选择文献[15]中ZDT1函数和ZDT2函数作为测试函数进行分析: ZDT1函数为 (7) ZDT2函数为 (8) 变量个数n=30,变量xi∈[0,1],i=1,2,…,30。在Gr-μMOGA算法中,其参数设置为:初始种群P1为8,外部种群Pe为100,交叉概率Pc为0.95,变异概率Pm为0.1,外部种群出现相同次数M为3,每个目标空间划分成相等个数的子空间,取Dk为5。采用NSGA-Ⅱ算法作对比分析,其初始种群P1为50,其余参数设置与Gr-μMOGA相同,都采用单点交叉和位变异操作。 (a)NSGA-Ⅱ算法求解ZDT1函数的Pareto解(b)Gr-μMOGA算法求解ZDT1函数的Pareto解 (c)NSGA-Ⅱ算法求解ZDT2函数的Pareto解(d)Gr-μMOGA算法求解ZDT2函数的Pareto解图4 ZDT1函数和ZDT2函数的优化结果 3.2三目标测试函数 采用文献[16]中的DTLZ1函数和DTLZ2函数进行分析,DTLZ1函数为 (9) i=1,2,…,n DTLZ2函数为 (10) i=1,2,…,n 式(9)和式(10)中的g(xm)分别为 cos(20π(xi-0.5))] xm=(xm,xm+1,…,xn) 3.3制动器多目标优化设计 汽车盘式制动器相对鼓式制动器,具有散热能力强、结构简单以及较高的方向稳定性等优点,被广泛用于现代汽车制动系统中。制动器在汽车制动过程中起着关键性作用,制动器质量、制动时间、制动圆盘半径等设计参数直接决定制动器的制动性能。制动器的啮合力越大,制动时间就越短,则需要更大的质量承受较大的啮合力,故制动器的啮合力、制动时间和总质量为多目标优化问题。本文引入文献[17]中的盘式制动器的优化问题,设计变量为制动器圆盘内径、外径、啮合力、摩擦接触面的个数,其多目标优化模型为 f3(x)=x3 式中,f1(x)为制动器的质量,kg;f2(x)为制动器的制动时间,s;f3(x)为制动器的啮合力,N;x1为制动器圆盘的内半径,mm;x2为制动器圆盘的外半径,mm;x3为制动器的啮合力,N;x4为摩擦接触面的个数。 (a)NSGA-Ⅱ算法求解DTLZ1函数的Pareto解 (b)Gr-μMOGA 算法求解DTLZ1函数的Pareto解 (c)NSGA-Ⅱ算法求解DTLZ2函数的Pareto解 (d)Gr-μMOGA算法求解DTLZ2函数的Pareto解图5 DTLZ1函数和DTLZ2函数的优化结果 其几何约束g1(x)和g2(x)为 g1(x)=(x2-x1)-20≥0 g2(x)=30-2.5(x4+1)≥0 压力约束g3(x)为 温度约束g4(x)为 扭矩约束g5(x)为 边界约束如下:55 mm≤x1≤80 mm,75 mm≤x2≤110 mm,1000 N≤x3≤3000 N,x4为[2,20]之间的整数。 将Gr-μMOGA算法用于求解制动器多目标优化问题,其Pareto最优解较好地分布于目标空间,如图6所示。表1给出了图6中的部分Pareto解。当设计者偏重于考虑制动器产生的制动力较小时可以选择解1。解6的制动力为2988.4N,制动时间为2.1s,质量为2.9kg,其制动时间最短,有利于汽车在紧急情况下快速制动。最终,设计者可以根据不同的设计需求选择相应的Pareto最优解。 图6 盘式制动器多目标优化结果 序号质量(kg)制动时间(s)制动力(N)设计变量(x1,x2,x3,x4)14.15.11365.556.6,108.1,1365.5,1121.63.62085.469.5,90.3,2085.4,1133.12.82265.775.3,109.9,2265.7,1143.72.62490.866.7,110,2490.8,1152.12.62821.965.4,93,2821.9,1162.92.12988.477.3,109.8,2988.4,11 3.4汽车高速和低速耐撞性多目标优化设计 制动器具有较好的制动性,能有效地避免汽车发生碰撞。当碰撞无法避免时,其保险杠、防撞梁和吸能盒等相关部件应能最大限度地保护乘员和汽车,降低损伤成本。采用文献[18]中汽车高速和低速耐撞性多目标优化设计模型,其中选取保险杠厚度x1、吸能盒内板厚度x2、吸能盒外板厚度x3、前纵梁内板厚度x4和前纵梁外板厚度x5为优化设计变量,如图7所示。高速碰撞模型为汽车以56 km/h的速度100%正面刚性壁障碰撞;低速碰撞模型为RCAR (Research Council for Automobile Repairs)中的正面偏置碰撞,如图8所示。选取汽车保险杠和前纵梁等部件的轻量化设计与碰撞中座椅点的加速度积分均值为多目标优化问题,其优化模型为[18] (11) 图7 优化设计变量 图8 汽车偏置碰撞模型 图9 汽车耐撞性多目标优化结果 表2 耐撞性优化部分Pareto最优解 本文提出了一种基于网格支配的微型多目标遗传方法Gr-μMOGA,该算法可用于求解多目标函数的优化问题。测试函数的结果表明,该算法具有较好的收敛性,在保证解的均匀性条件下可提高计算效率。采用本文提出的算法求解制动器和汽车高低速耐撞性多目标优化设计问题,获得了较好的非支配解集。在实际工程设计中,工程人员可以根据不同的设计方案选择相应的Pareto解以满足设计要求。 [1]王炳刚, 饶运清, 邵新宇, 等. 基于多目标遗传算法的混流加工/装配系统排序问题研究[J]. 中国机械工程, 2009, 20(12): 1434-1438. Wang Binggang, Rao Yunqing, Shao Xinyu, et al. A MOGA- based Algorithm for Sequencing a Mixed-model Fabrication/ Assembly System[J]. China Mechanical Engineering, 2009, 20(12): 1434-1438. [2]张勇, 李光耀, 王建华. 多目标遗传算法在整车轻量化优化设计中的应用研究[J]. 中国机械工程,2009,20(4): 500-503. Zhang Yong, Li Guangyao, Wang Jianhua. Design Optimization on Lightweight of Full Vehicle Based on Multi- objective Genetic Algorithm[J]. China Mechanical Engineering, 2009,20(4): 500-503. [3]陈建岭, 孙杰, 李剑峰. 钛合金铣削加工参数多目标优化研究[J]. 中国机械工程, 2014, 25(2): 169-773. Chen Jianling, Sun Jie, Li Jianfeng. Multi-objective Optimization of Cutting Parameters during Milling of Titanium Alloys[J]. China Mechanical Engineering, 2014, 25(2): 169-773. [4]Schafer J D. Multiple Objective Optimization with Vector Evaluated Genetic Algorithms[C]//Proceedings of 1st International Conference on Genetic Algorithms and Their Applications. Pittsburgh, PA, USA, 1985: 93-100. [5]Deb K, Pratap A, Agrwal S, et al. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197. [6]Zitzler E, Laumanns M, Thiele L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm for Multiobjective Optimization[C]//Evolutionary Methods Design Optimization Control, Proceedings EUROGEN 2001.Athens,Greece,2001:95-100. [7]谢然, 兰凤崇, 陈吉清, 等. 满足可靠性要求的轻量化车身结构多目标优化方法[J]. 机械工程学报, 2011, 47(4): 117-124. Xie Ran, Lan Fengchong, Chen Jiqing, et al. Multi-objective Optimization Method in Car-body Structure Light-weight Design with Reliability Requirement[J]. Chinese Journal of Mechanical Enineering, 2011, 47(4): 117-124. [8]刘桂萍, 韩旭, 姜潮. 基于微型多目标遗传算法的薄板冲压成形变压边力优化[J]. 中国机械工程, 2007, 18(21): 2614-2617. Liu Guiping, Han Xu, Jiang Chao. Optimization of Variable Binder Force in Sheet Metal Forming Using the Micro Multi-objective Genetic Algorithm[J]. China Mechanical Engineering, 2007, 18(21): 2614-2617. [9]Liu Guiping, Han Xu, Jiang Chao. A Novel Multi-objective Optimization Method Based on an Approximation Model Management Technique[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(33): 2719-2731. [10]刘桂萍, 韩旭, 官凤娇. 基于信赖域近似模型管理的多目标优化方法及其应用[J]. 中国机械工程, 2008, 19(10): 1140-1143. Liu Guiping, Han Xu, Guan Fengjiao. A multi-objective optimization Method Based on the Trust Region Model Management Framework and Its Applicatio[J]. China Mechanical Engineering, 2008, 19(10): 1140-1143. [11]Krishnakumar K. Micro-genetic Algorithms for Stationary and Non-stationary Function Optimization[C] //SPIE Proceedings: Intelligent Control and Adaptive Systems.Philadelphia, US, 1989: 289-296. [12]Yang S X, Li M Q, Liu X H, et al. A Grid-Based Evolutionary Algorithm for Many-Objective Optimization[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(5): 721-736. [13]Miettinen K. Nonlinear Multiobjective Optimization[M].New York: Kluwer Academic Publishers, 1999. [14]Li M Q, Zheng J H, Shen R M, et al. A Grid-Based Fitness Strategy for Evolutionary Many-Objective Optimization[C]//Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation.New York, 2010:463-470. [15]Zitzler E, Deb K, Thiele L. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results[J]. IEEE Transactions on Evolutionary Computation, 2000, 8: 173 -195. [16]Deb K, Thiele L, Laumanns M, et al. Scalable Multi-objective Optimization Test Problems[C]// Proceedings of the 2002 Congress on Evolutionary Computational.Honolulu, 2002:825-830. [17]Osycaka A, Kundu S.A Modified Distance Method for Multicriteria Optimization Using Genetic Algorithms[J]. Computers & Industrial Engineering, 1996, 30:871-882. [18]姜潮, 邓善良. 考虑车辆高速和低速耐撞性的多目标优化设计[J]. 计算力学学报, 2014,31(4): 474-479.Jiang Chao, Deng Shanliang. Multi-objective Optimization and Design Considering Automotive High-speed and Low-speed Crashworthiness[J].Chinese Journal of Computational Mechanics, 2014, 31(4): 474-479. (编辑苏卫国) Micro Multi-objective Genetic Algorithm Based on Grid Domination Fu ChunmingJiang ChaoLiu GuipingDeng Shanliang State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha,410082 A micro multi-objective genetic algorithm was proposed herein based on grid domination to solve multi-objective optimization problems and it had good convergence and high computational efficiency. The method combined with the concept of the grid dominance and micro multi-objective genetic algorithm. In each generation, the grid value, the grid crowding distance and grid coordinate point distance of every individual were calculated, respectively. Then elite individuals were selected to do crossover and mutation operators based on the grid domination sorting and grid selection strategies. The individuals were iterated toward the Pareto front and the Pareto optimal solutions were obtained. Finally, the proposed algorithm was verified effectively through four test functions and two practical engineering problems. multi-objective genetic algorithm; grid domination; micro population; Pareto optimal solution; crashworthiness 2014-06-05 国家自然科学基金资助项目(11172096);国家自然科学基金优秀青年基金资助项目(51222502);教育部新世纪优秀人才支持计划资助项目(NCET-11-0124);湖南省杰出青年基金资助项目(14JJ1016) TP18DOI:10.3969/j.issn.1004-132X.2015.16.014 符纯明,男,1987年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生。研究方向为差分进化算法、多目标优化。姜潮(通信作者),男,1978年生。湖南大学汽车车身先进设计制造国家重点实验室教授、博士研究生导师。刘桂萍,女,1980年生。湖南大学汽车车身先进设计制造国家重点实验室讲师。邓善良,男,1987年生。湖南大学汽车车身先进设计制造国家重点实验室硕士研究生。2 Gr-μMOGA算法及构造
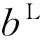
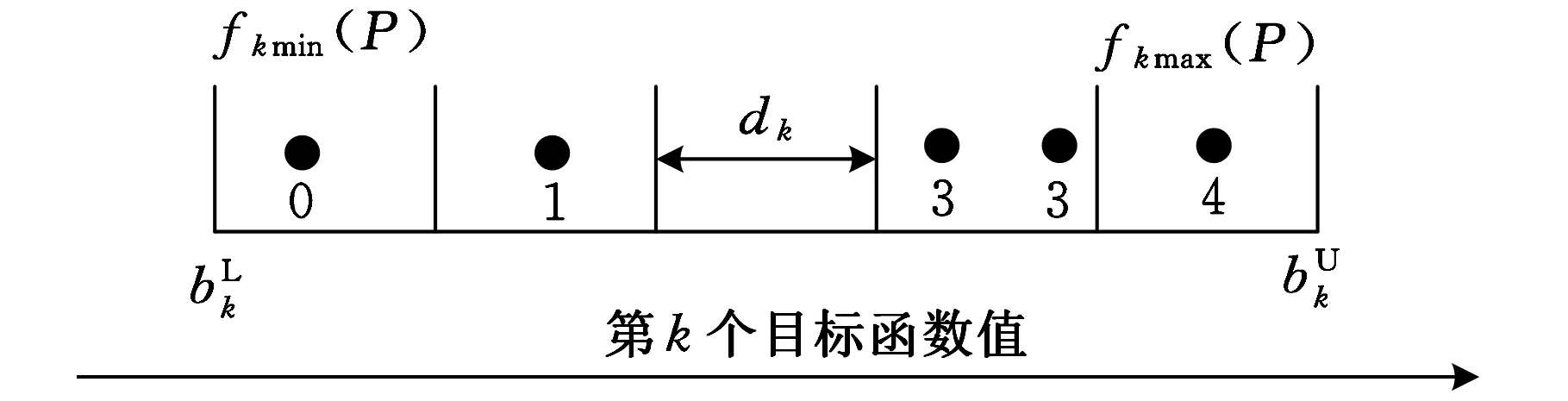

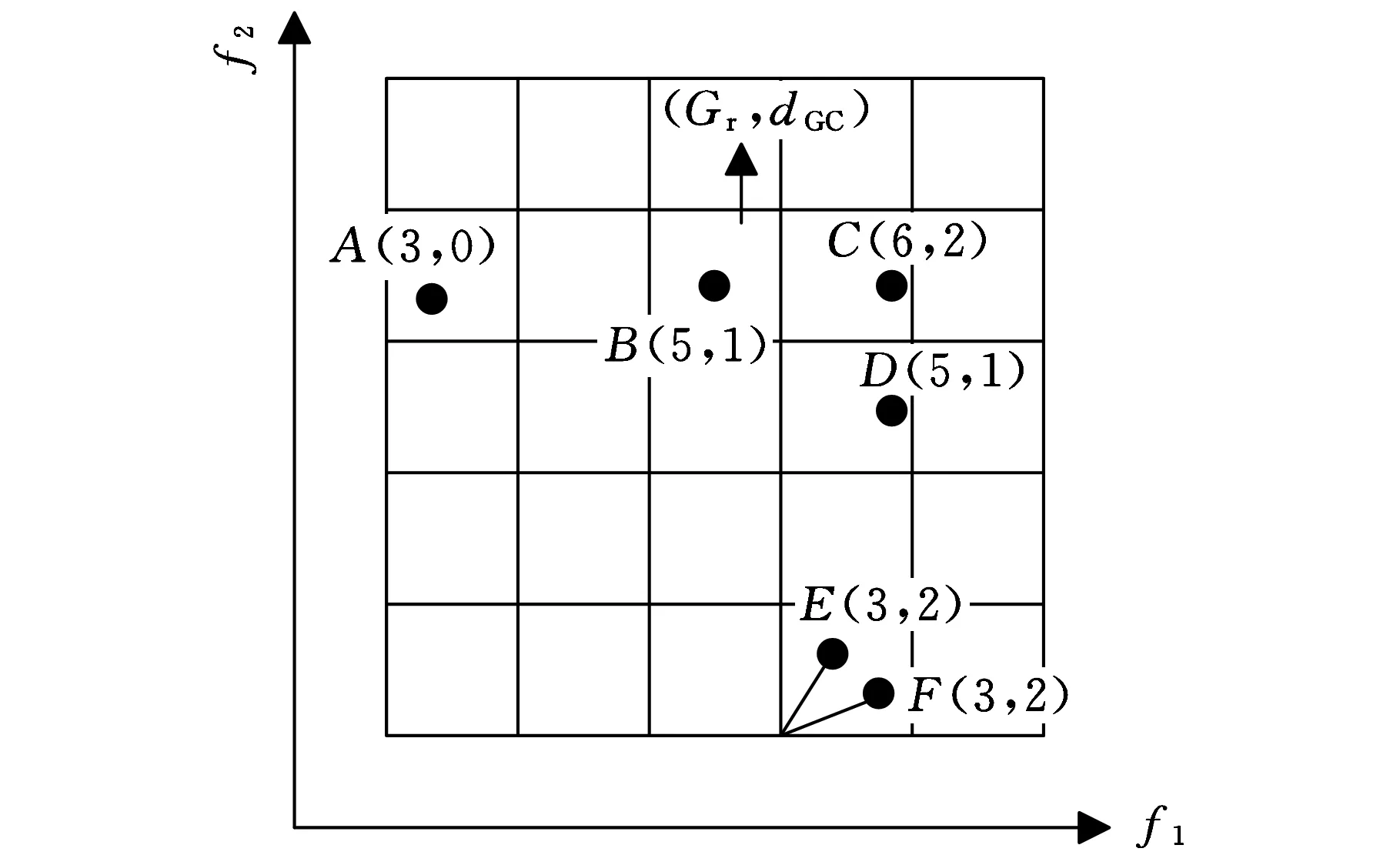
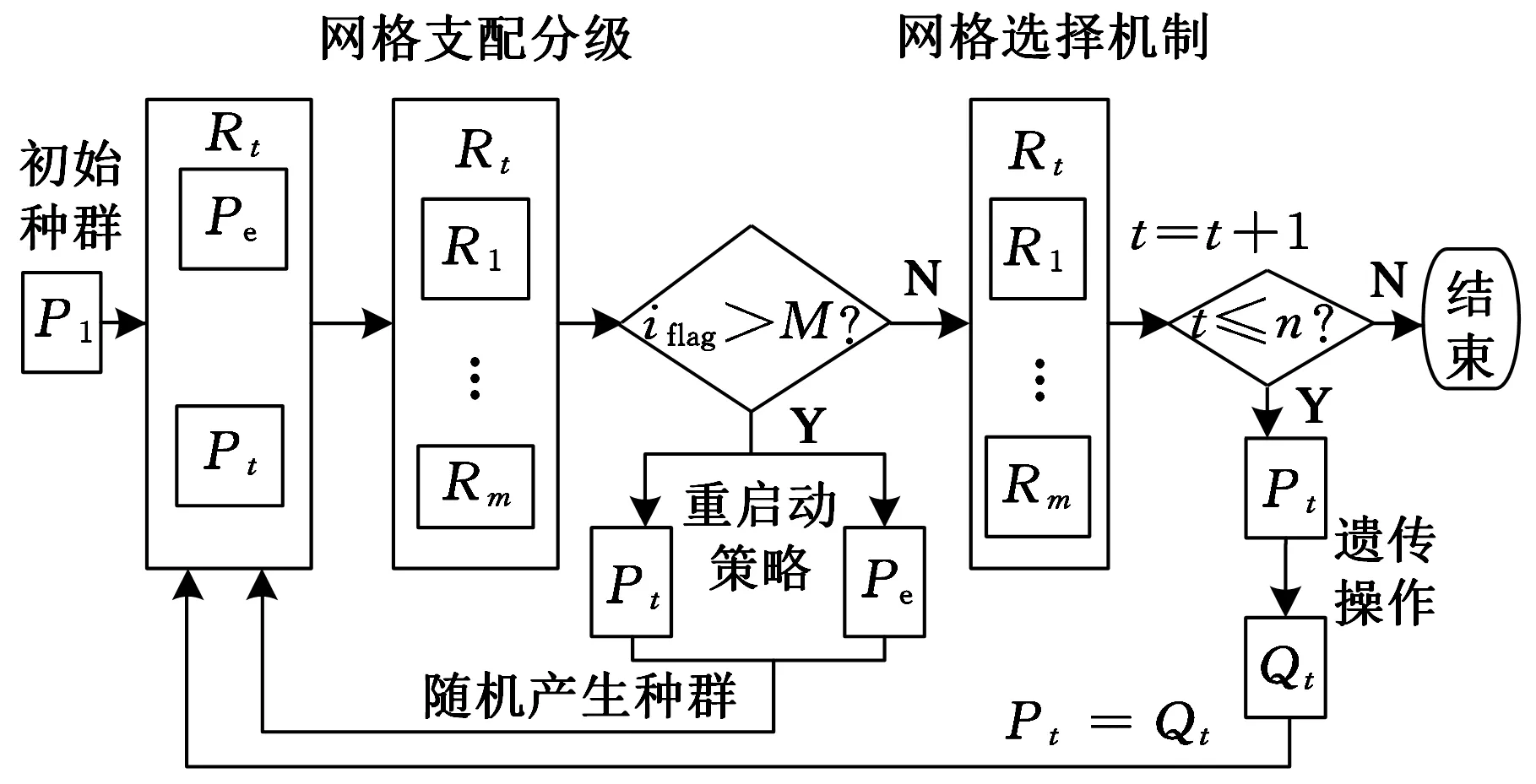
3 测试函数及工程应用
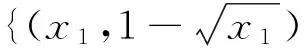

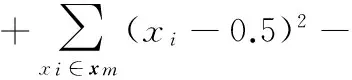
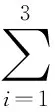

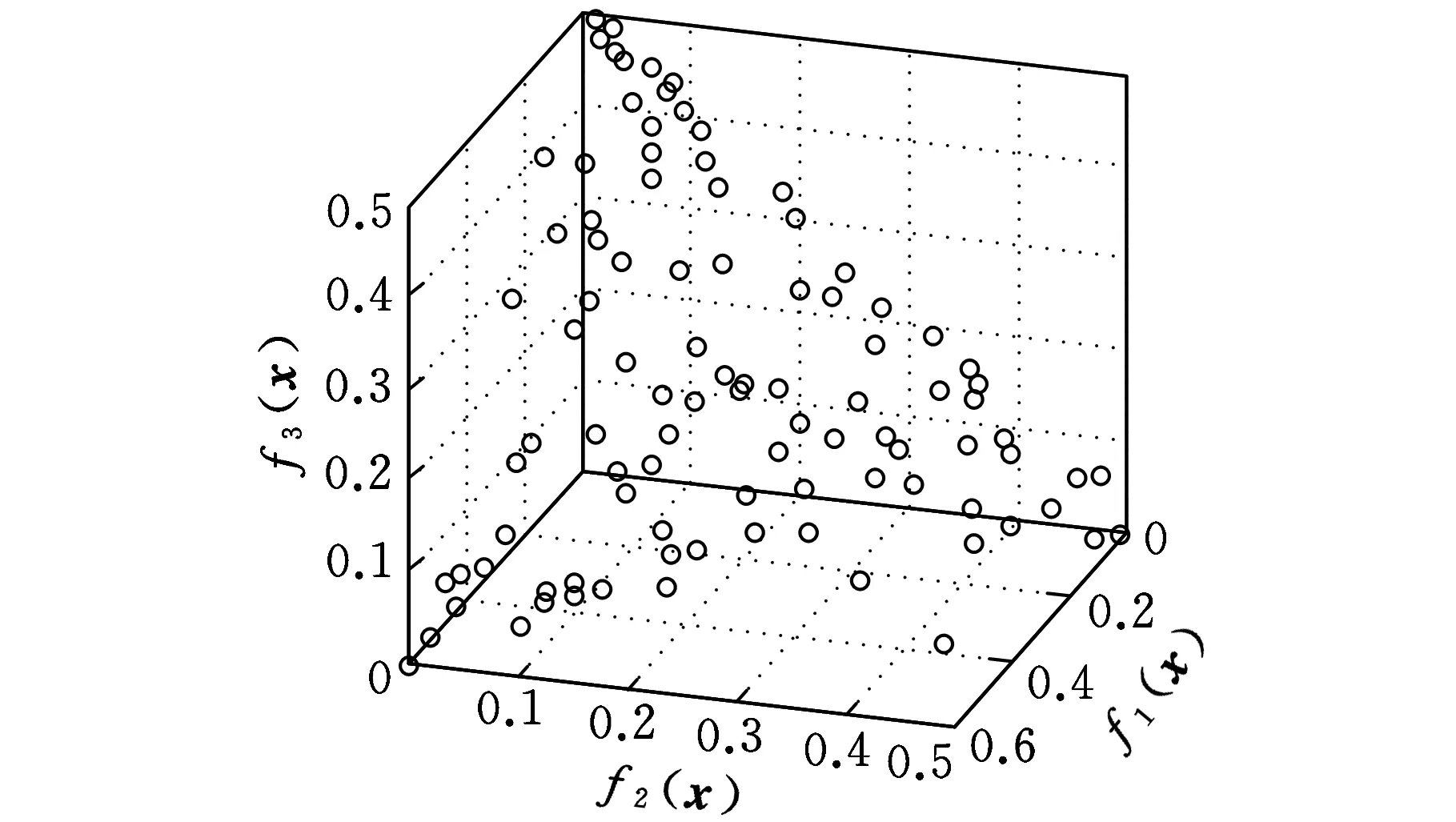

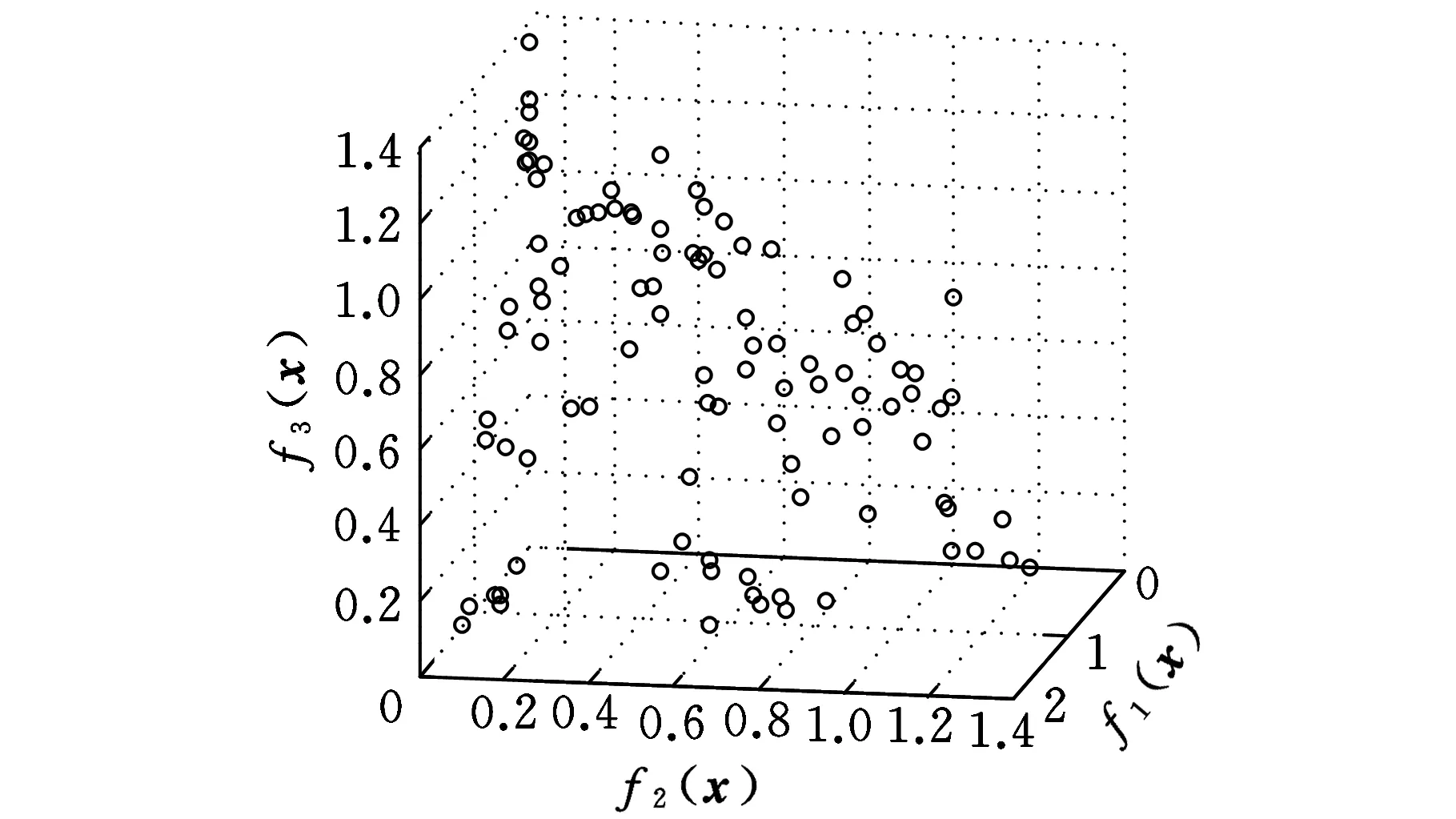
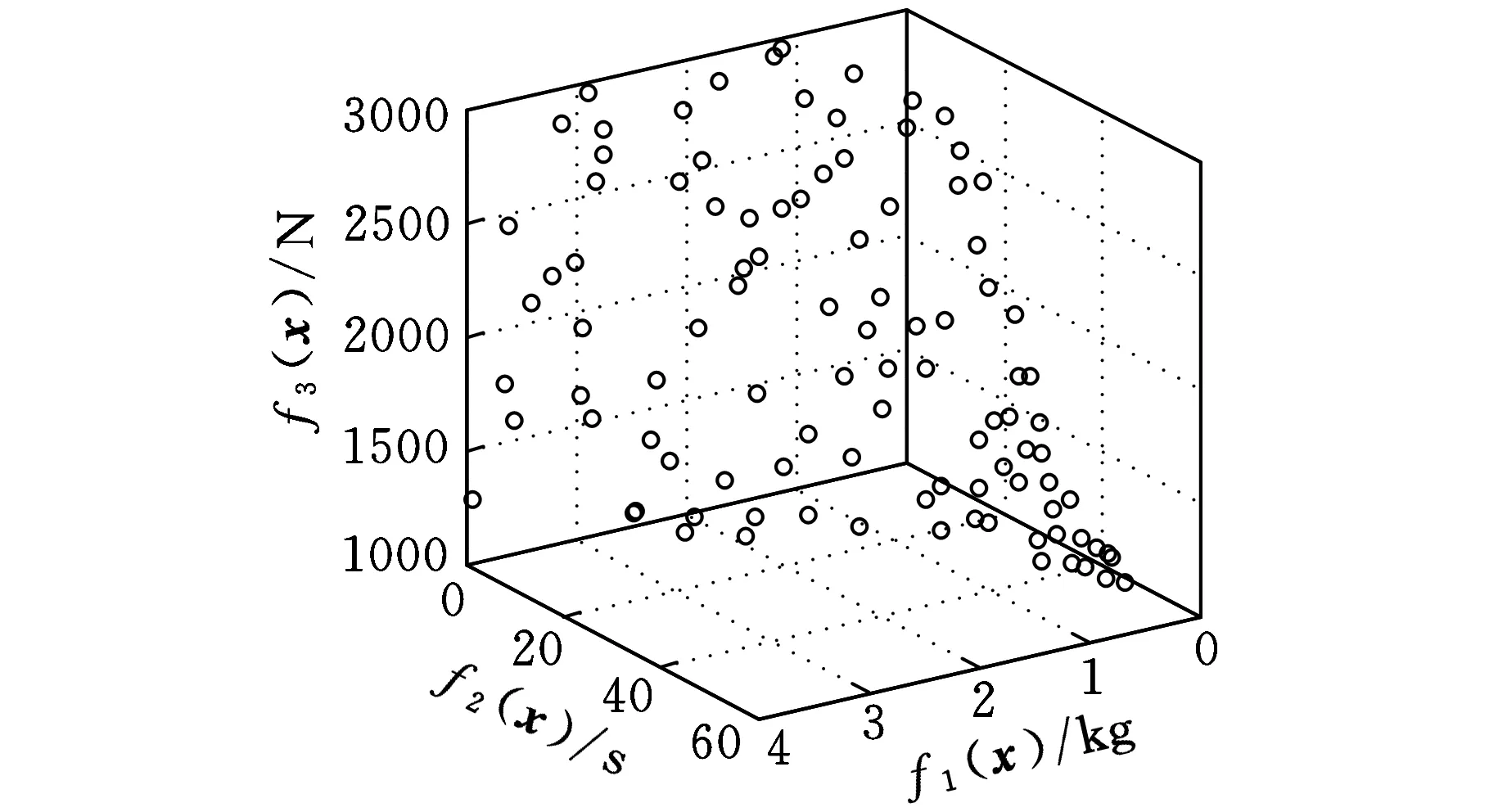
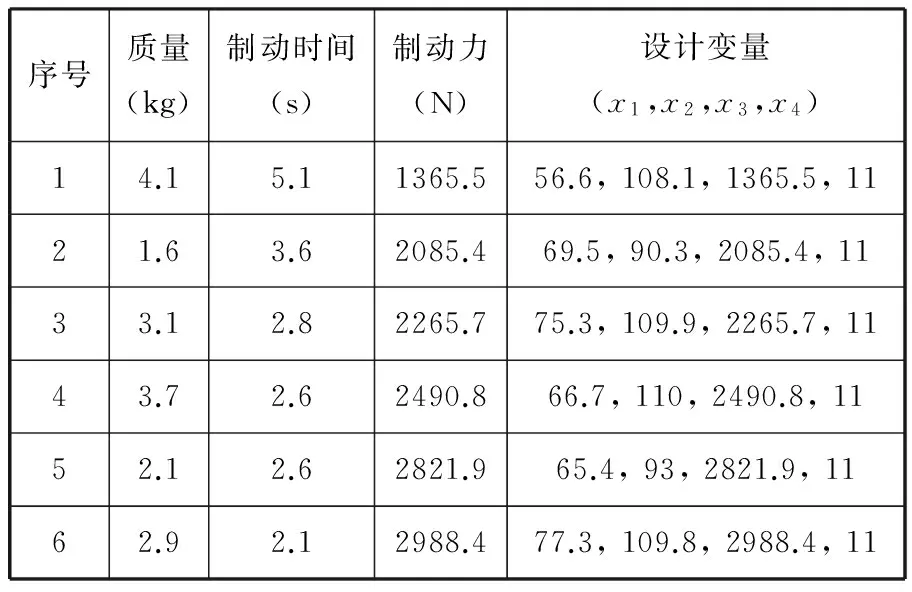


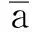
4 结语
