基于道路误差动力学模型智能车辆横向切换LMIs/H∞转向控制策略

汪选要　王其东

1.合肥工业大学，合肥，230009　　2.安徽理工大学，淮南，232001

基于道路误差动力学模型智能车辆横向切换LMIs/H∞转向控制策略

汪选要1,2王其东1,2

1.合肥工业大学，合肥，2300092.安徽理工大学，淮南，232001

基于道路误差动力学模型对不确定线性车辆模型设计了横向切换转向控制器，所提出的控制律包括车道中心线到车辆质心距离的切换PIDey控制和车辆相对车道方向误差的切换PDeψ控制，以车辆理论横摆角速度作为扰动项，控制策略利用状态反馈γ-次优H∞范数和线性矩阵不等式LMIs约束获得线性目标函数凸优化问题的最优解和相应的最小扰动抑制度γ。采用CarSim中的Alt3 from FHWA道路模型和D-Class/Sedan车辆模型获取参考速度，为了简化模型，仅以时变速度子模型作为横向切换转向控制器的切换信号，在低附着系数道路上以10自由度车辆动力学模型验证了基于道路误差动力学模型比基于L2WVM(linear two-wheel vehicle model) 所设计的横向控制律具有更高的路径跟踪精度和稳定性，通过改变车辆模型参数验证了基于道路误差动力学模型切换H∞控制器比L2WVM控制器具有更好的鲁棒性。

横向切换转向控制；道路误差动力学模型；状态反馈γ-次优H∞范数；LMIs约束；时变速度

0　引言

日常生活中汽车使用数量急剧增加，带来了一系列新的问题，如安全和乘坐舒适性、交通管理以及燃油消耗排放和环境保护等，为了应对这些挑战，人们开发了一系列主动和被动辅助系统，如ABS、ESP、ACC以及四轮转向系统。如今，车辆自动驾驶成为国内外研究的热点，尤其在车辆自动驾驶的核心内容——汽车纵向控制和横向控制方面取得了很多研究进展[1]。李琳辉等[2]建立了基于视觉预瞄距离的车辆横向控制系统模型，综合考虑车辆当前的横向偏差和方位偏差作为滑模切换函数的参数来设计滑模面。王立标等[3]设计了一种自适应神经网络控制器, 通过直接对横摆力矩和前轮主动转向进行复合控制来提高车辆横向稳定性。陈无畏等[4-5]在车辆当前行驶位置和道路预瞄点之间实时规划逼近目标路径的虚拟路径，基于单点预瞄最优曲率模型设计了侧向加速度PD跟踪控制器并基于7自由度非线性车辆动力学模型设计了滑模控制器，以跟踪期望横摆角速度，实现对车辆的横向控制。Chou等[6]通过使用制动器设计了非线性底盘控制器以跟踪期望的路径，但无主动转向控制。Cerone等[7]设计了一个驾驶员模型，能够实现车道保持和主动避障。Marino等[8]提出了基于二阶解耦控制器的转向控制。Enache等[9]提出基于转向力矩控制方法实现转向控制。上述研究很少关注变化的车辆结构参数和高动态负载下控制器的性能。切换系统通常用于很难设计模型控制律的场合，它采用有限数量的局部模型和转换规则来实现模型转换。切换系统属于混合系统类型，Koenig等[10]和Lin等[11]研究了其稳定性和相关的设计问题，Apkarian等[12]基于标准H∞范数和线性矩阵不等式(linear matrix inequalities，LMIs)提出了一种解决线性变参数(linear parameter-varying，LPV)系统控制问题的方法。

本文基于道路误差动力学模型对不确定线性车辆模型设计横向切换转向控制器，控制系统以转向角作为输入，以车道中心线到车辆质心的距离偏差ey和车辆相对车道的方向误差eψ作为输出，所提出的控制律包括基于ey的切换PID控制和基于eψ切换的PD控制，纵向速度被用于确定PIDey控制器和PDeψ控制器的切换信号。控制策略利用LMIs约束和状态反馈γ-次优H∞范数获得线性目标函数凸优化问题的最优解和相应的最小扰动抑制度γ。通过低附着系数路面和较大的纵侧向加速度来验证控制系统的路径跟踪精度和稳定性，通过改变整车质量m和横摆转动惯量Iz来验证所设计控制器的鲁棒性。

1　车辆道路误差动力学模型

在一般驾驶情况下，车辆前后轮侧向力[13]可表示为

(1)

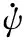
令ey为车道中心线到车辆质心的距离，eψ为相对车道的车辆方向误差，道路误差变量的状态方程模型可表示为

(2)

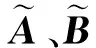
(3)

其中，σ为选择适当局部模型的切换信号[14]。LPV模型稳定性分析详见文献[13]。

2　切换控制器设计

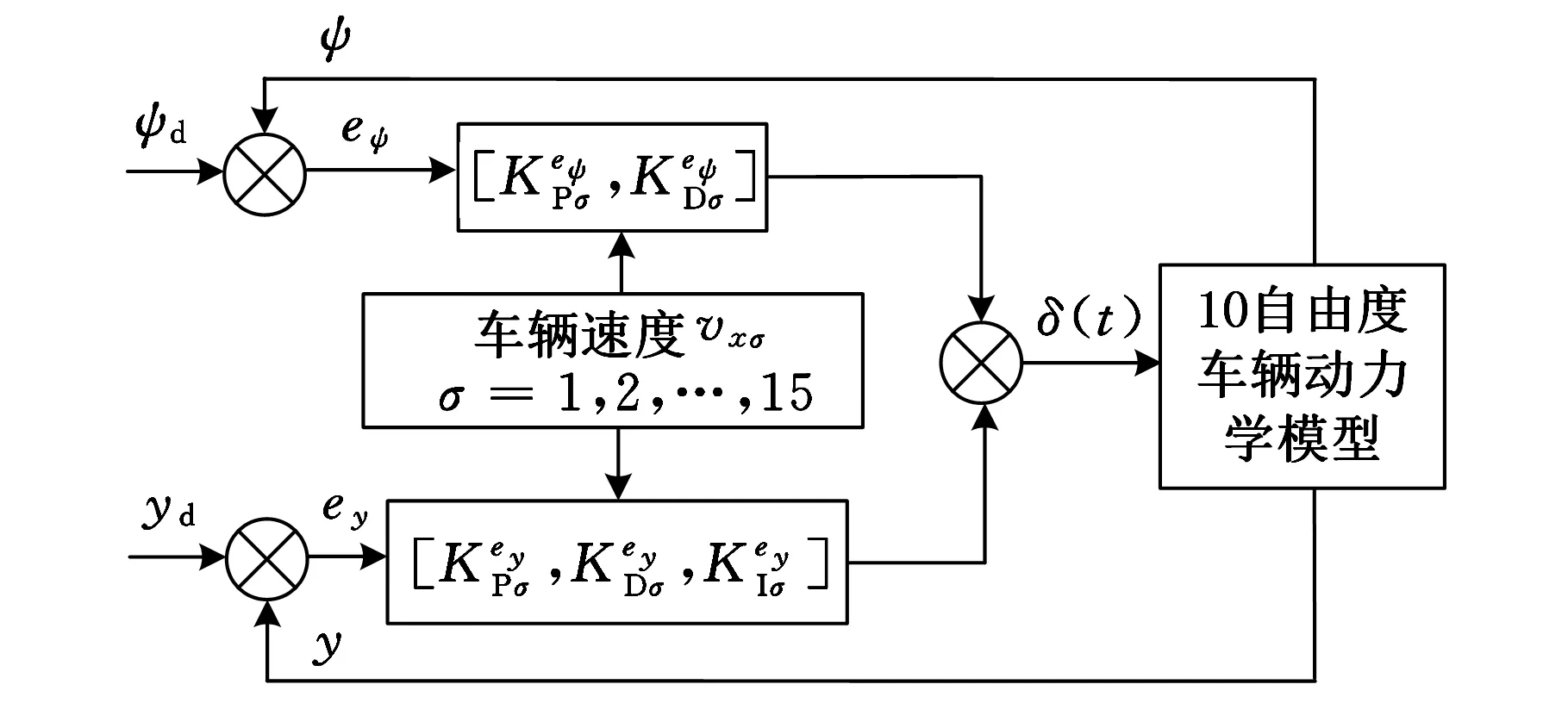
图1　横向切换转向控制流程

横向切换PIDey和PDeψ控制器的控制策略如图1所示，在切换控制器设计过程中仅考虑了纵向速度的变化。期望横摆角ψd和期望车道中心线到车辆质心的距离yd详见文献[15]。根据纵向车速实时地切换PIDey和PDeψ控制器参数，速度范围vx(t)∈[5,50]m/s，其分隔区间数量M=15。令σ=1,2,…,15，不同切换点的纵向速度上界可表示为

(4)

其中，Σ为分隔不同切换点的速度区间，Σ=3。例如，当σ=4时车速区间为[14,17]，区间中间点速度为15.5 m/s。

引入积分项eyI=∫eydt来衰减系统横向位置稳态误差，扩展式(3)的状态向量可得切换、不确定线性系统如下：

(5)

3　状态反馈γ-次优H∞控制器

假设系统的状态误差可以直接测量得到，设计一个静状态反馈控制器u(t)=-Kσxe，得到相应的闭环系统:

(6)

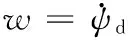
问题转化为：对于给定参考信号，使得扰动的影响最小。对于给定的标量γ>0，系统闭环传递函数Tzx(s)满足

‖γ-1C1σ[sI-(Aσ+B2σK)]-1B1σ‖∞<1

(7)

当且仅当存在一个对称正定矩阵X和矩阵W，使得以下的矩阵不等式成立：

(8)

Ω=AσX+B2σW+(AσX+B2σW)T

如果矩阵不等式存在一个可行解X*、W*，则系统的状态反馈γ-次优H∞控制器u*(t)=-W*(X*)-1xe(t)。根据状态反馈γ-次优H∞控制器存在的条件，通过求解以下优化问题：

(9)

利用LMIs约束和线性目标函数凸优化问题的最优解可以得到该系统的最优H∞控制器和相应的最小扰动抑制度γ。系统初始状态xe(0)还需满足[16]

(10)

式中，ε为目标函数正上限。

根据Schur引理可得

(11)

在高动态负载极端驾驶条件下车辆模型的转向角不得大于δmax[17]，假设u(t)=δ(t)=-WX-1xe(t)是以上LMIs约束的解，因此通过Schur引理可得

(12)

PIDey和PDeψ控制器参数通过求解式(9)～式(12)所示的一系列LMIs约束的优化问题获得：

(13)

在系统扩展模型中，静状态反馈增益Kσ包括所有的PIDey和PDeψ控制器参数:

(14)

4　10自由度动力学仿真模型

为了测试和评估所设计的控制器的性能，采用10自由度动力学仿真模型[18]，包括纵向、横向和垂向运动，侧倾、俯仰和横摆运动(侧倾角、俯仰角和横摆角分别为φ、θ和ψ)以及4个车轮的旋转运动，令ij=fl,fr,rl,rr(fl、fr分别表示前左轮和前右轮，rl、rr分别表示后左轮和后右轮)，纵向、侧向与垂向动力学方程分别为

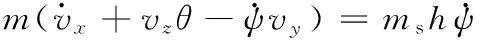
∑Fxij+mgsin(φr-θr)

(15)

mgsin(θr-φr)cos(φr-θr)

(16)

(17)

式中,vy、vz分别为车辆质心处的横向和垂向速度；ms为簧上质量；θr、φr分别为道路坡度角和倾斜角；h为质心高度；Fxij、Fyij和Fzij分别为车辆坐标系中的轮胎纵向力、侧向力和垂向力；g为重力加速度。

侧倾、俯仰和横摆动力学方程分别为

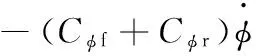
(18)

(19)

(20)

式中，Ix、Iy、Ixz分别为车身侧倾转动惯量、俯仰转动惯量、车身侧倾与横摆运动惯性积；Kφ f、Kφ r分别为前后悬架侧倾刚度；Cφ f、Cφ r分别为前后悬架侧倾阻尼；Mzij、Czij分别为轮胎力产生的横摆力矩和阻力矩。

车轮旋转运动动力学方程为

(21)

式中，Iw为车轮转动惯量；R为轮胎半径；Fxwij为车轮坐标系中轮胎纵向力，轮胎力由魔术公式[13]获得；Twij为车轮驱动或制动力矩。

4个车轮垂向力分别为

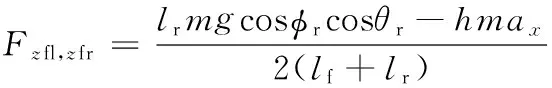
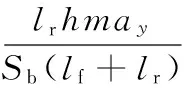
(22)

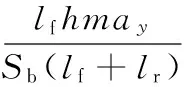
(23)

式中,ax、ay分别为车辆坐标系纵向和横向加速度；Sb为轮距。

车辆模型参数如表1所示，状态反馈增益由式(9)～式(12)通过LMI工具箱求解，如表2所示。

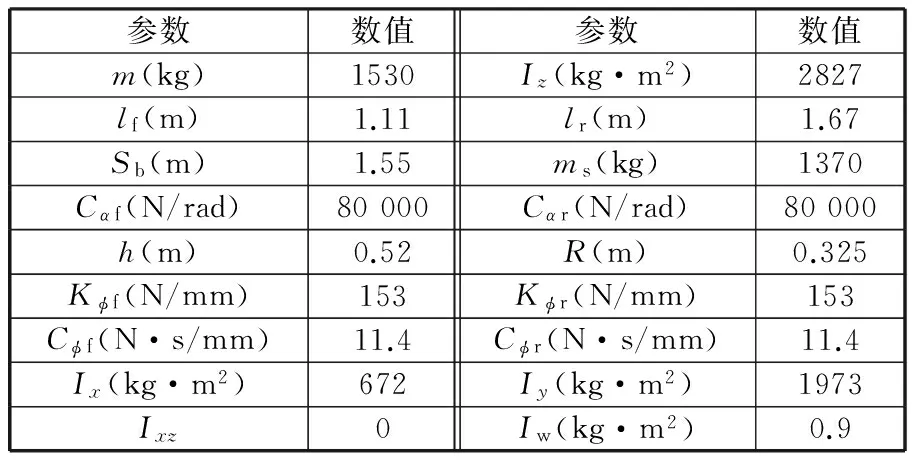
表1　车辆模型参数

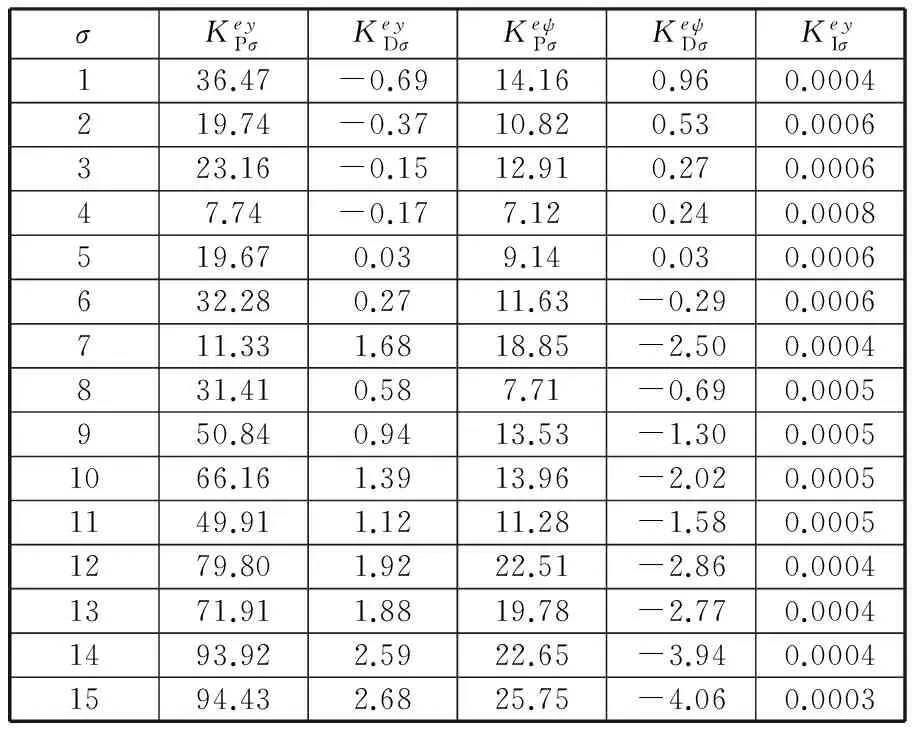
表2　控制器参数

5　仿真试验与CarSim数据对比

CarSim仿真中车辆模型采用D-Class/Sedan，驾驶员控制模型分别采用NormalDriving和0.7/0.3GMaxAx/AyLimits，仿真时间分别为56s和48s，道路模型为Alt3fromFHWA，路面附着系数μ=0.85，以此获得参考速度1和参考速度2，如图2所示。根据式(4)可得参考车速1和参考车速2的PIDey和PDeψ控制器的切换信号如图3所示，通过LMIs优化可得最小扰动抑制度γ=1.7，在MATLAB/Simulink仿真环境中建立车辆模型并对切换H∞控制与L2WVM控制进行对比仿真试验。

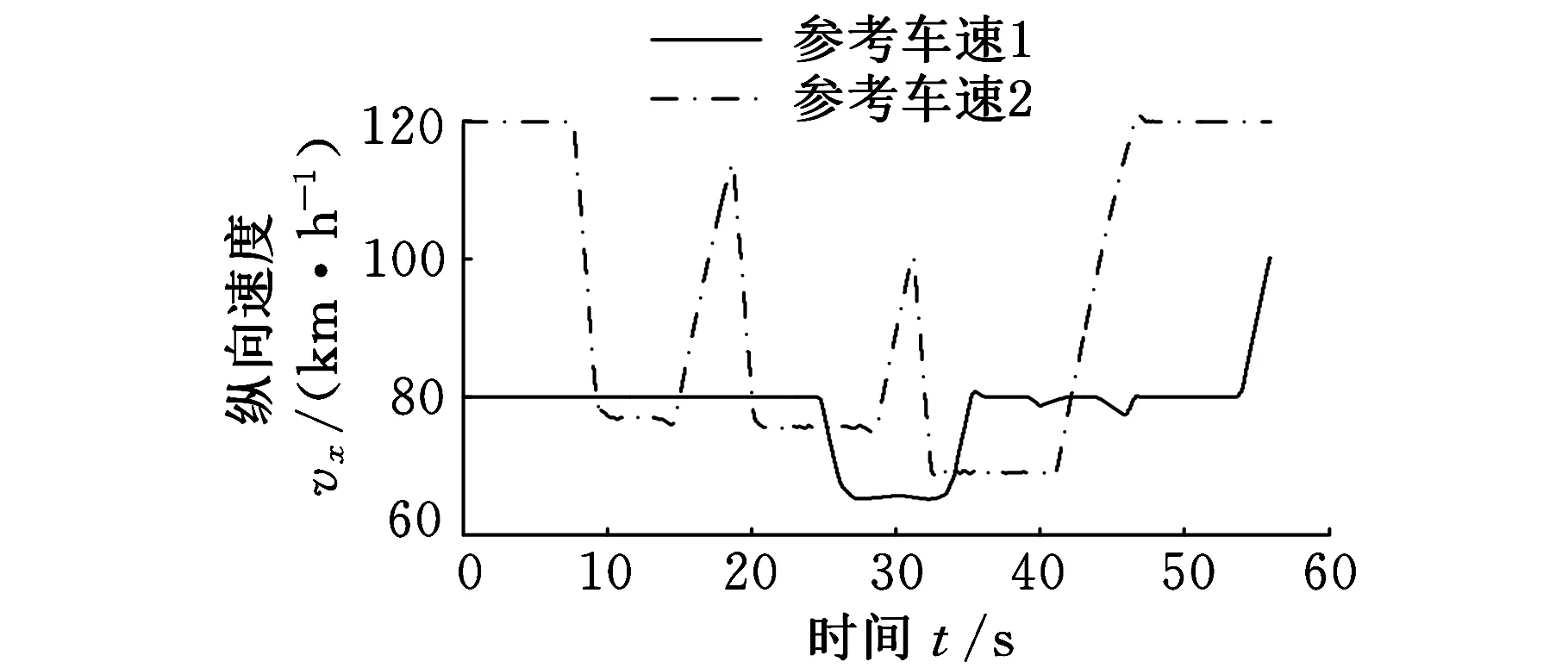
图2　纵向参考车速

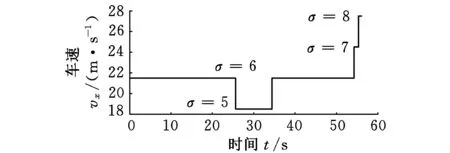
(a)Normal Driving

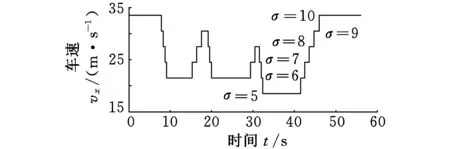
(b)0.7/0.3GMax Ax/Ay Limits图3　切换信号

对所设计的横向切换控制器分别基于Menhour等[16]的L2WVM模型(lineartwo-wheelvehiclemodel)和道路误差动力学模型进行仿真，并与CarSim横向控制模型进行对比。为了节约篇幅，仅对比了参考车速2下的性能指标。图4、图5验证了路面附着系数μ=0.85时两种控制器的路径跟踪能力和纵向车速跟踪能力。

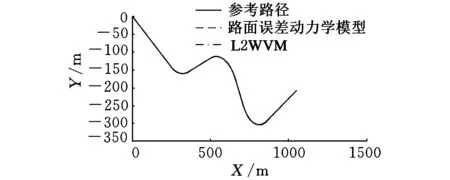
(a)路径跟踪

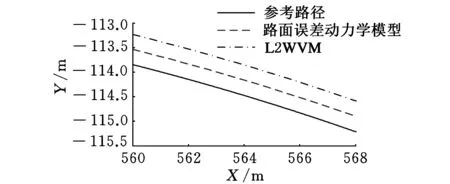
(b)局部放大图4　路径跟踪轨迹和局部放大图(μ=0.85)

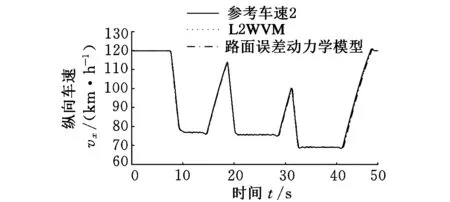
(a)车速跟踪

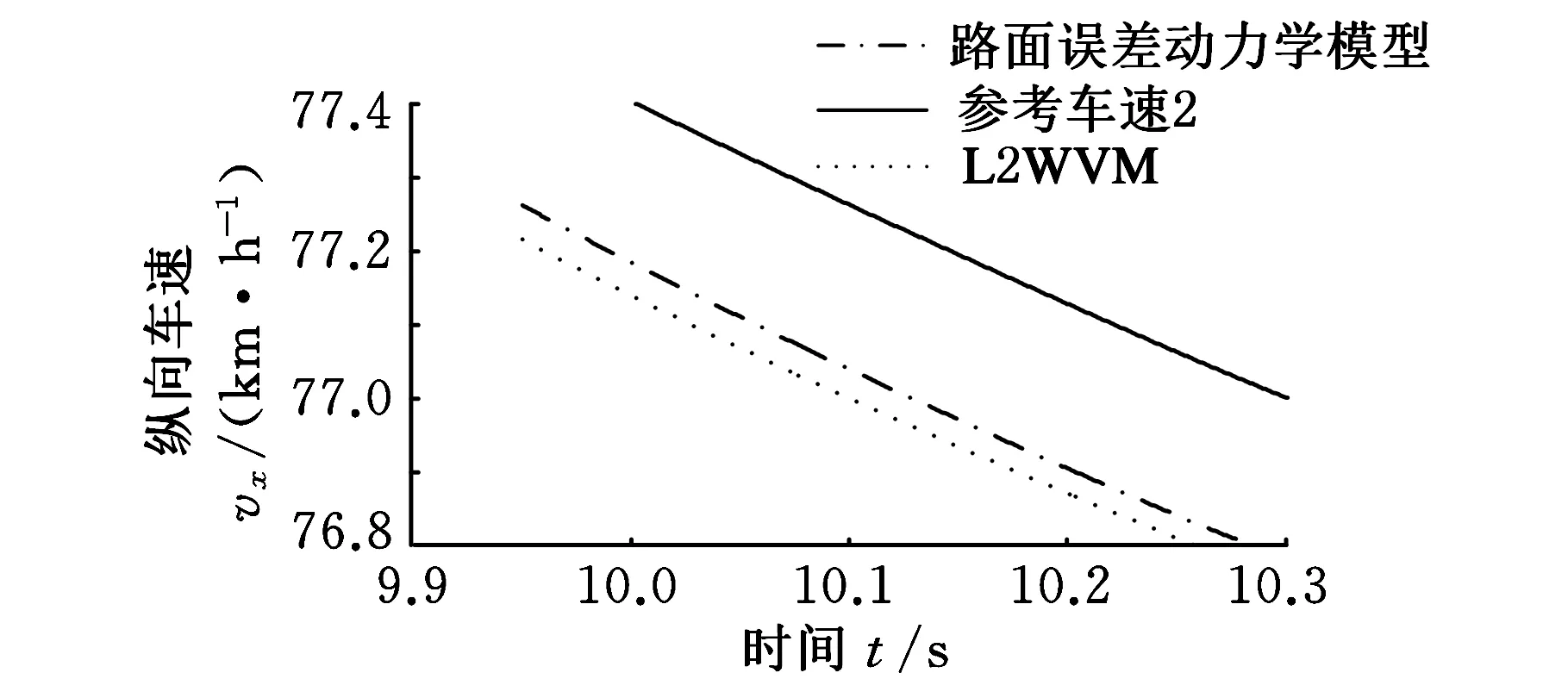
(b)局部放大图5　纵向车速跟踪和局部放大图(μ=0.85)

由图6～图8可以看出，基于道路误差动力学模型控制器即使在大动态负载情况下(侧向加速度超过0.3g)也能保证系统的稳定性。由图9、图10可以看出，采用道路误差动力学模型控制律在低附着系数(μ=0.5)路面上有较高的路径跟踪精度。

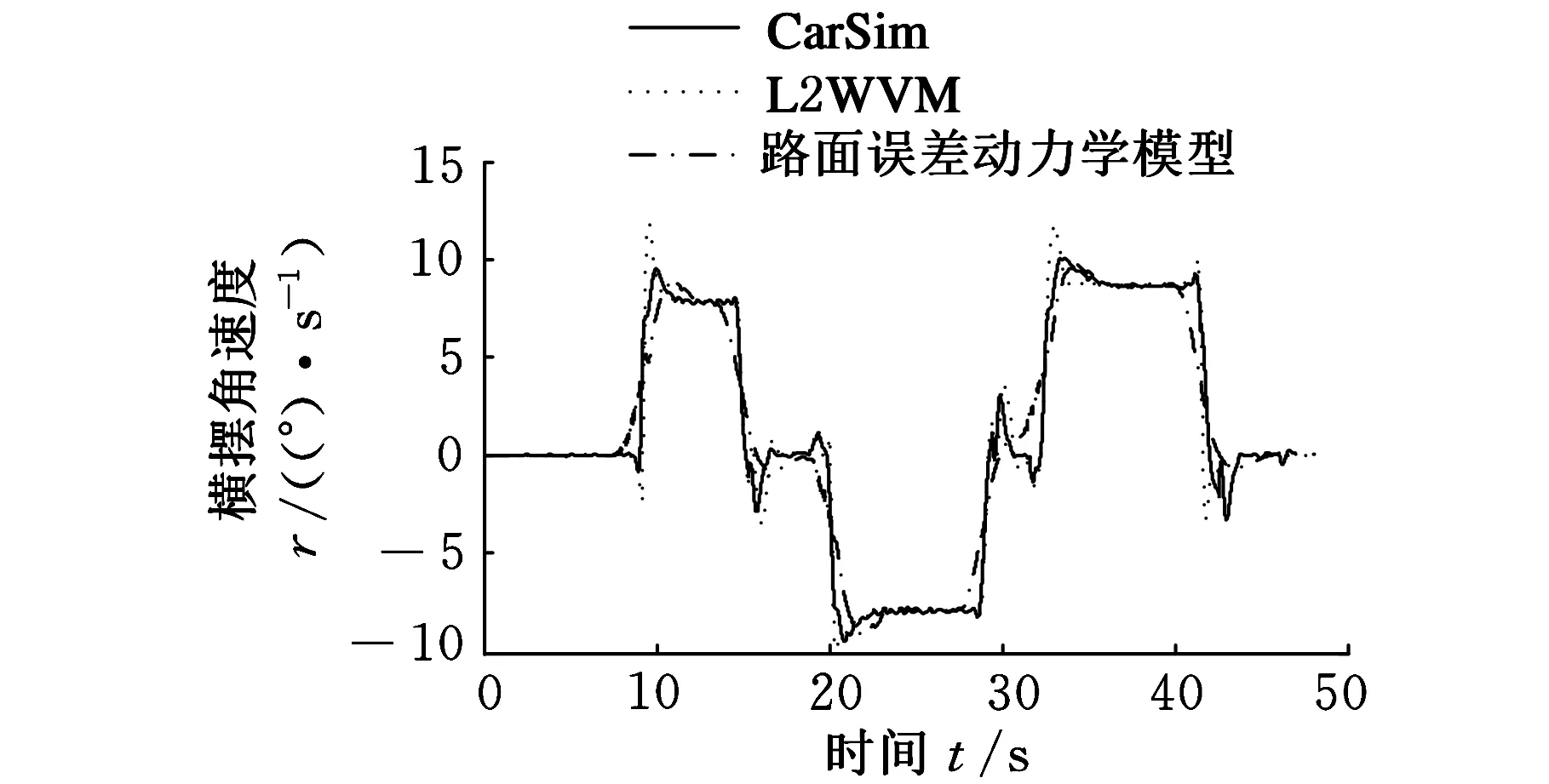
图6　横摆角速度(μ=0.85)

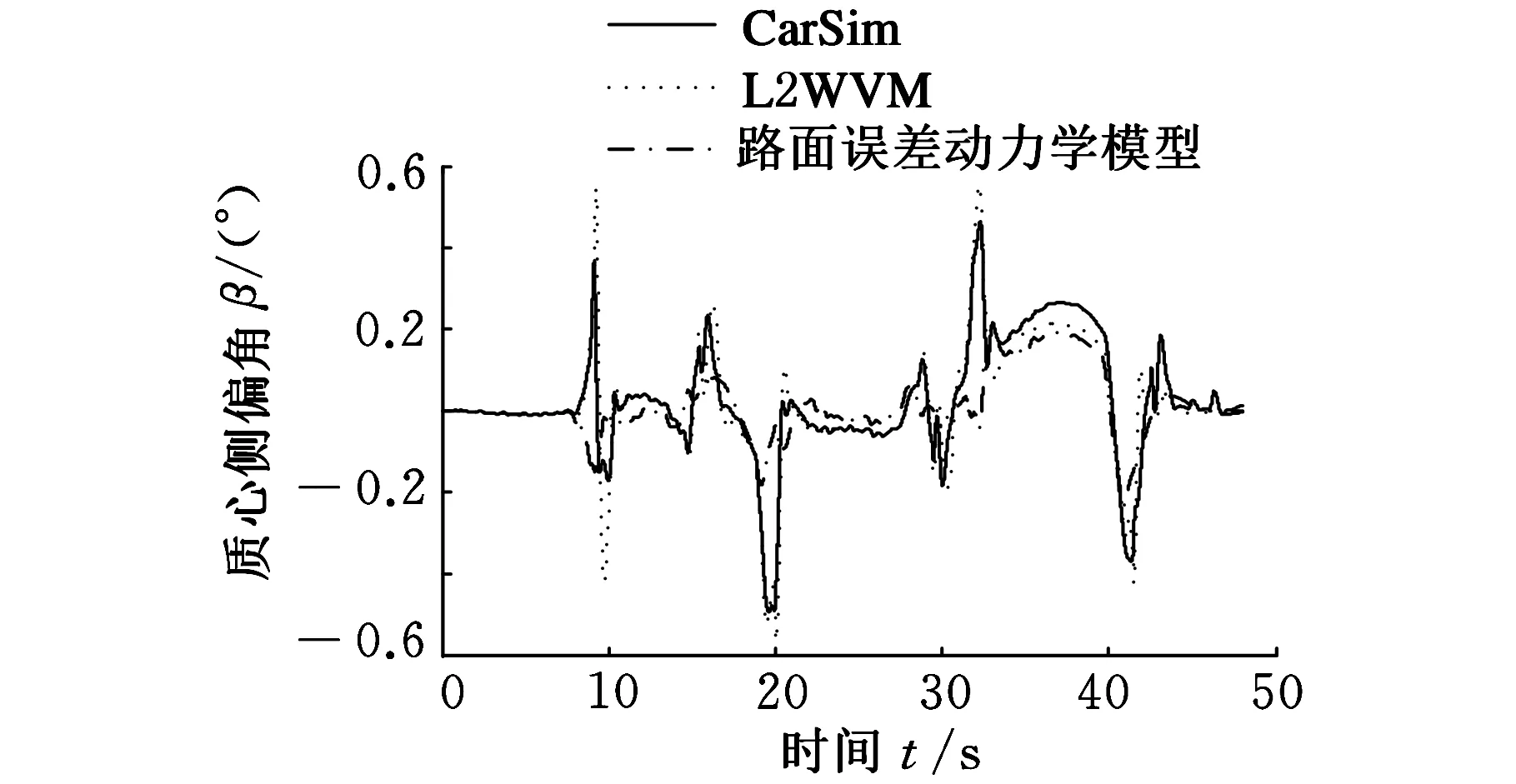
图7　质心侧偏角(μ=0.85)

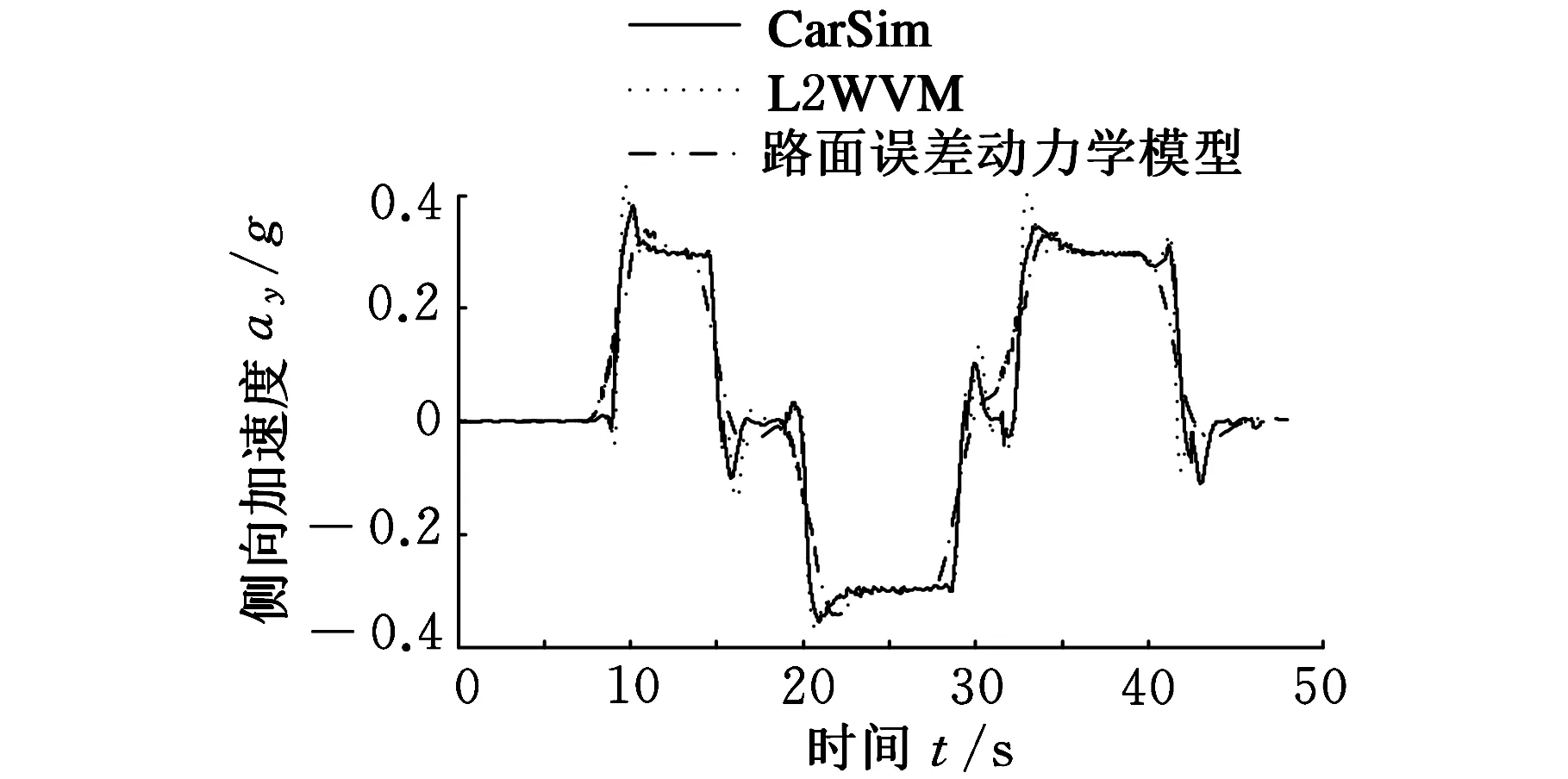
图8　侧向加速度(μ=0.85)

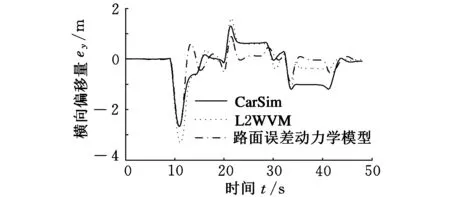
图9　横向偏移量(μ=0.5)

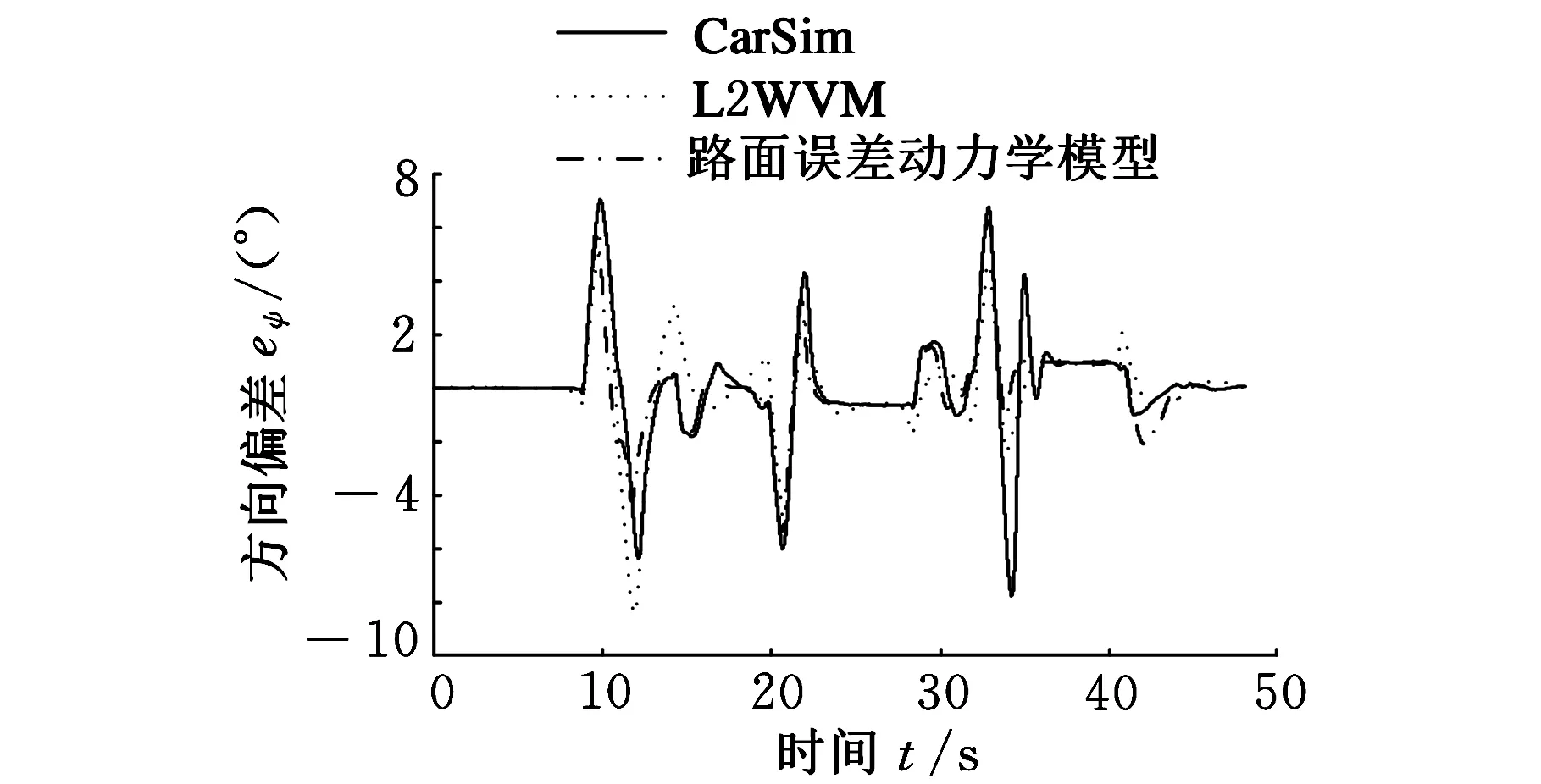
图10　方向角误差(μ=0.5)

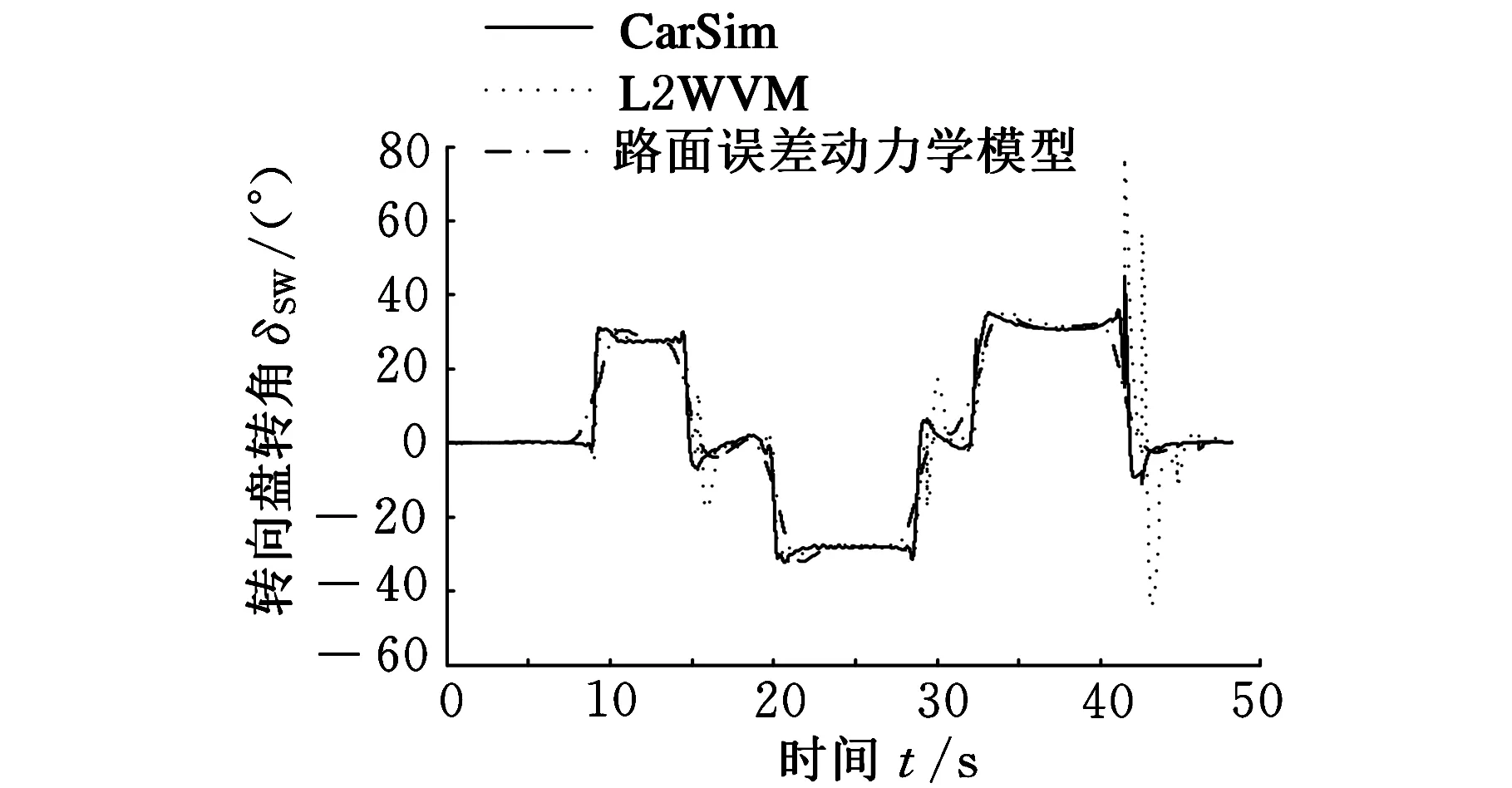
图11　转向盘转角(μ=0.7)

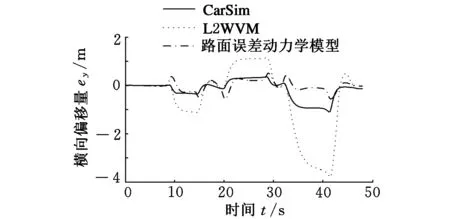
图12　横向偏移量(μ=0.7)

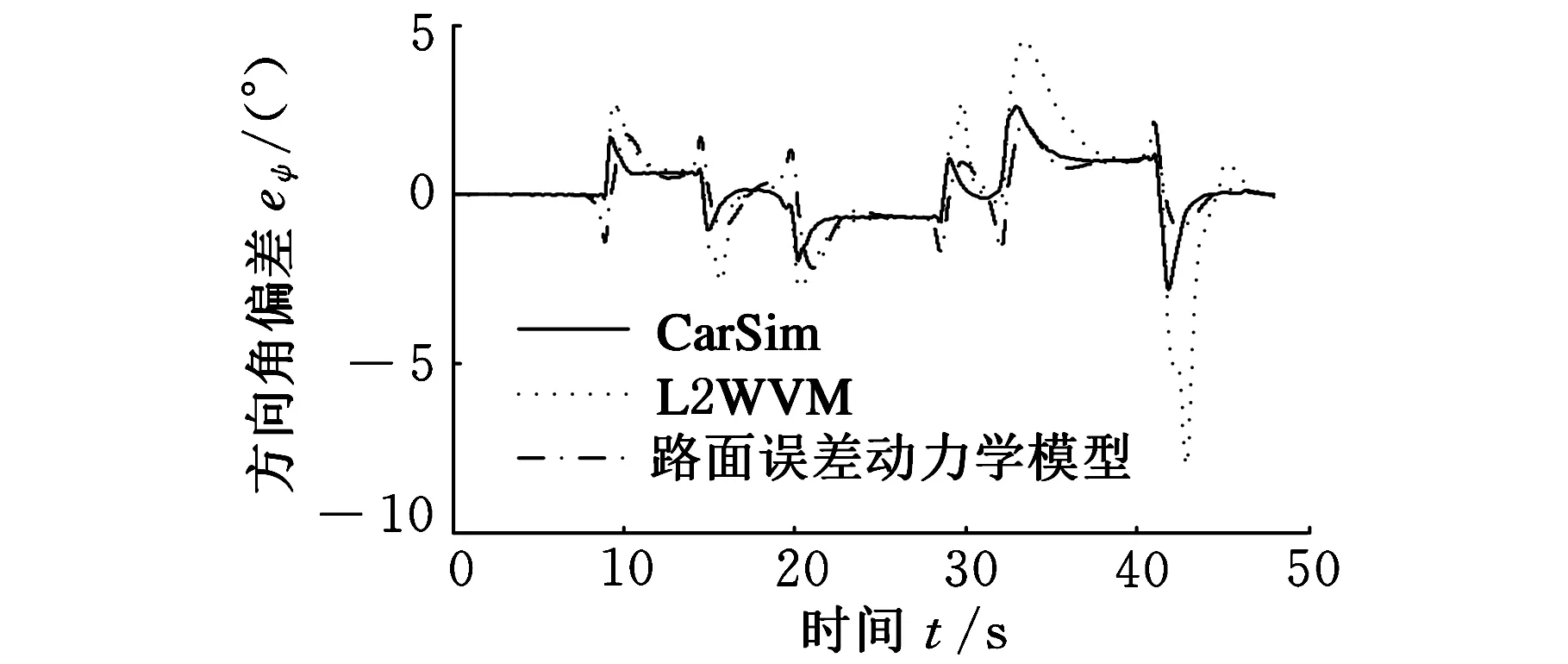
图13　方向角误差(μ=0.7)

为了验证控制模型在不确定结构参数下的鲁棒性，将整车质量和转动惯量增大20%，采用路面附着系数μ=0.7进行仿真，结果如图11～图13所示，可以看出，采用L2WVM控制器的转向盘转角出现了很大的跳动，横向偏移量甚至达到了3.8m，方向角误差超过了6.5°，误差已经大大超出了期望值的范围，而基于道路误差动力学模型控制器的路径跟踪误差较小，显示了良好的鲁棒性。

表3、表4所示为两种横向切换控制器在参考车速为1和2时的横向偏移量ey和方向角误差eψ的均值和方差，可以看出，采用L2WVM控制器跟踪参考车速2比跟踪参考车速1时的均值和方差明显增大，而道路误差动力学模型在跟踪不同车速时均值和方差变化较小，表明该方法受车速变化的影响较小。同时还可以看出，对于参考车速2，两种控制方法的均值和方差均增大，这是因为该参考车速仅仅受0.7g最大纵向加速度和0.3g最大横向加速度限制，车速变化范围大，非一般驾驶工况，而基于道路误差动力学模型横向偏移和方向角误差始终小于基于L2WVM控制器的横向位移偏差和方向角误差，在参考车速2时最大横向偏差仅为0.68m,最大方向角误差为2.9°。

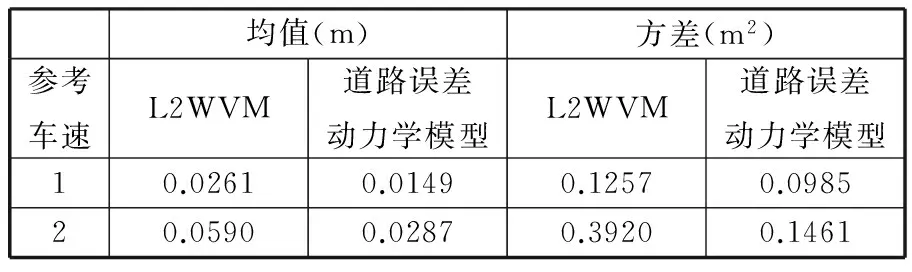
表3　横向偏移ey

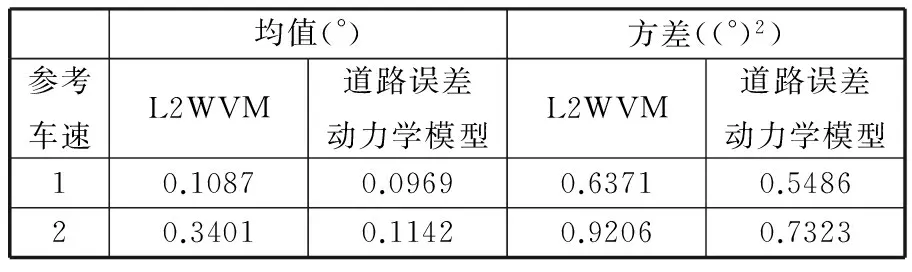
表4　方向角误差eψ

6　结论

(1)提出了基于道路误差动力学模型的横向切换控制策略，基于线性矩阵不等式LMI/H∞设计了横向偏移量PIDey控制器和方向角误差PDeψ控制器，该控制方法的关键是求LMIs约束和线性目标函数凸优化的最优解。

(2)与L2WVM控制器相比，在低附着系数路面上基于道路误差动力学模型的横向控制器具有更高的路径跟踪精度，跟踪道路偏差随着车辆速度及道路曲率的变化波动范围小，从而验证了该模型的稳定性。

(3)对于变化的车辆结构参数，基于道路误差动力学模型横向控制具有更好的鲁棒性，主要是因为基于道路误差动力学模型以车辆理论横摆角速度作为扰动项，而L2WVM的扰动项较多。

(4)为了简化模型,仅以时变速度子模型作为道路误差动力学模型，当车辆处于高动态负载时，轮胎侧偏刚度与侧偏角将变成非线性关系，考虑这种非线性关系的道路误差动力学模型有待进一步研究。

[1]Katriniok A, Abel D. LTV-MPC Approach for Lateral Vehicle Guidance by Front Steering at the Limits of Vehicle Dynamics[C]//2011 50th IEEE Conference on Decision and Control and European Control Conference, CDC-ECC 2011.Orlando, FL, 2011: 6828-6833.

[2]李琳辉, 李明, 郭景华, 等. 基于视觉的智能车辆模糊滑模横向控制[J]. 大连理工大学学报, 2013, 53(5): 735-741.

Li Linhui, Li Ming, Guo Jinghua, et al. Fuzzy Sliding Mode Lateral Control of Intelligent Vehicle Based on Vision[J]. Journal of Dalian University of Technology, 2013, 53(5): 735-741.

[3]王立标, 李军, 范剑, 等. 车辆横向稳定性自适应神经网络控制策略研究[J]. 汽车工程, 2010, 32(6): 493-496.

Wang Libiao, Li Jun, Fan Jian, et al. A Study on the Control Strategy of Adaptive Neural Network for Vehicle Yaw Stability[J]. Automotive Engineering, 2010, 32(6): 493-496.

[4]王家恩, 陈无畏, 王檀彬, 等. 基于期望横摆角速度的视觉导航智能车辆横向控制[J]. 机械工程学报, 2012, 48(4): 108-115.

Wang Jia’en, Chen Wuwei, Wang Tanbin, et al. Vision Guided Intelligent Vehicle Lateral Control Based on Desired Yaw Rate[J]. Journal of Mechanical Engineering, 2012, 48(4): 108-115.

[5]陈无畏, 王家恩, 汪明磊, 等. 视觉导航智能车辆横向运动的自适应预瞄控制[J]. 中国机械工程, 2014, 25(5): 698-704.

Chen Wuwei, Wang Jia’en, Wang Minglei, et al. Adaptive Preview Control of Vision Guided Intelligent Vehicle Lateral Movement[J]. China Mechanical Engineering, 2014, 25(5): 698-704.

[6]Chou H, d′Andréa-Novel B. Global Vehicle Control Using Differential Braking Torques and Active Suspension Forces[J]. Vehicle System Dynamics, 2005, 43(4): 261-284.

[7]Cerone V, Milanese M. Combined Automatic Lane-keeping and Driver’s Steering Through a 2-DOF Control Strategy[J]. IEEE Transactionson Control Systems Technology, 2009, 17(1): 135-142.

[8]Marino R, Cinili F. Input-output Decoupling Control by Measurement Feedback in Four Wheel-steering-vehicles[J]. IEEE Transactions on Control Systems Technology, 2009, 17(5): 1163-1172.

[9]Enache N, Sebsadji Y, Mammar S, et al. Driver’s Influence on the Performance of an Integrated Lane Departure Avoidance and Lane Keeping Assistance System[C]//18th IEEE International Conference on Control Applications, Part of 2009 IEEE Multi-conference on Systems and Control. Saint Petersburg, Russia, 2009: 119-124.

[10]Koenig D, Marx B, Jacquet D. Unknown Input Observers for Switched Nonlinear Discrete Time Descriptor Systems[J]. IEEE Transactions on Automatic Control, 2008, 53(1): 373-379.

[11]Lin H, Antsaklis P J. Stability and Stabilizability of Switched Linear Systems: a Survey of Recent Results[J]. IEEE Transactions on Automatic Control, 2009, 54(2):308-322.

[12]Apkarian P, Gahinet P, Becker G. Self-scheduledH∞Control of Linear Parameter-varying Systems: a Design Example[J]. Automatica, 1995, 31(9): 1251-1261.

[13]王国业, 江发潮, 等. 车辆动力学及控制[M]. 北京：机械工业出版社, 2010.

[14]Sun Z, Ge S S Analysis and Synthesis of Switched Linear Control Systems[J]. Automatica, 2005, 41(2): 181-195.

[15]Menhour L, Lechner D, Charara A. Two Degrees of Freedom Pid Multi-controllers to Design a Mathematical Driver Model: Experimental Validation and Robustness Tests[J]. Vehicle System Dynamics, 2011, 49(4):595-624.

[16]Menhour L, Charara A, Lechner D. Switched LQR/H∞Steering Vehicle Control to Detect Critical Driving Situations[J]. Control Engineering Practice, 2014, 24(3): 1-14.

[17]Ackermann J, Guldner J, Wolfgang S. Linear and Nonlinear Controller Design for Robust Automatic Steering[J]. IEEE Transactions on Control Systems Technology, 1995, 3(1): 132-142.

[18]Menhour L, Brigitte D, Fliess M, et al. Coupled Nonlinear Vehicle Control: Flatness-based Setting with Algebraic Estimation Techniques[J]. Control Engineering Practice. 2014, 22(6):135-146.

(编辑苏卫国)

Lateral Switched LMIs/H∞Steering Control Strategy of Intelligent Vehicle Based on Path Error Dynamics Model

Wang Xuanyao1,2Wang Qidong1,2

1.Hefei University of Technology,Hefei,230009 2.Anhui University of Science and Technology,Huainan,Anhui,232001

Based on the path error dynamics model,a lateral switched steering controller was designed for an uncertain linear model of the vehicle, which included switched PIDeycontrol of the distance from the centerline of the lane to the center of mass of the vehicle, and switched PDeψcontrol of the direction errors from the lane to the vehicle. Setting the vehicle theoretic yawing angular velocity as the disturbance, the optimal solution of convex optimization problems of linear objective function, and the corresponding minimum disturbance rejectionγwere acquired for the control strategy, which the state feedbackγ-suboptimumH∞norm and linear matrix inequalities(LMIs) were used. The road model of Alt3 from FHWA was acquired from CarSim, and the reference velocity was obtained from the vehicle model D-Class/Sedan. In order to simplify the model, a sub-model with time-varying velocity was selected as the switching signal for the lateral switched steering controller. On the road with low adhesion coefficient, there were both verified with 10 degrees of freedom vehicle dynamics model, which was based on the path error dynamics model of the lateral control law and have higher path tracking accuracy and stability than L2WVM(linear two-wheel vehicle model). With the changed structure parameters of vehicle model, it is verified that the switchedH∞controller based on the path error dynamics model has better robustness than the L2WVM.

lateral switched steering control; path error dynamics model; state feedbackγ-suboptimumH∞norm; LMIs constraint; time-varying velocity

2014-06-04

国家自然科学基金资助项目(51075112，51405004)

U461DOI：10.3969/j.issn.1004-132X.2015.16.019

汪选要，男，1980年生。合肥工业大学机械与汽车工程学院博士研究生，安徽理工大学机械工程学院副教授。主要研究方向为车辆动力学与控制、汽车辅助驾驶技术。王其东，男，1964年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师，安徽理工大学机械工程学院教授、博士研究生导师。