结合模糊聚类和合作竞争博弈的优化方法

陈加明　宋小文　徐　浩

1.杭州职业技术学院,杭州,310000　　2.浙江大学,杭州,310027

结合模糊聚类和合作竞争博弈的优化方法

陈加明1宋小文2徐浩2

1.杭州职业技术学院,杭州,3100002.浙江大学,杭州,310027

针对多目标优化问题转化为博弈问题的难点，即博弈问题的各博弈方战略集的确定问题，利用均匀设计试验法、回归分析和F检验为模糊聚类提供数据基础，将多目标优化设计与博弈分析结合起来,提出了一种多目标优化方法。以减速器优化设计为例，对该方法的性能进行了分析与验证,并与传统单目标优化方法进行对比分析。结果表明,该方法收敛速度快，计算效率高，无需人为确定各目标权重，具有工程应用价值。

模糊聚类；合作竞争博弈；均匀设计；回归分析

0　引言

科学实践、工程设计及社会生产和经济发展中的许多问题都可以描述为优化问题，由于实际问题的复杂性,一般是具有多个优化目标、多个约束条件的多目标问题。现有的经典多目标优化解法主要都归结于多目标的线性组合，对Pareto最优前沿的形状很敏感，不能处理前沿的凹部，优化效率非常低,时间成本高，计算量巨大，并且求解问题时由于难以获得与应用背景相关的启发式知识信息，从而使优化效果差或者无法正常实施优化，尤其对于大规模问题，这些传统的多目标优化方法的应用非常少[1]。

多目标优化设计中，各目标之间一般是冲突的[2]。为了调和这些冲突，就需要以某种方式来解决各目标之间的矛盾。而博弈论是研究决策主体的行为在直接相互作用时，如何进行决策以及这种决策如何达到均衡的方法,目前博弈论在工程设计领域的应用已经越来越多。鉴于多目标优化问题和博弈问题的相似性，可以将博弈论思想和方法引入到工程多目标优化设计问题的求解之中，以克服传统多目标优化设计问题求解方法的不足。谢能刚等[3-4]根据Nash均衡模型和Stackelberg寡头博弈模型，建立了多目标博弈设计的技术路线和关键指标，并在补偿滑轮组变幅机构、汽车被动悬架系统的多目标优化设计中成功应用。

现有多目标优化问题的博弈分析中,将设计变量集合转化为各博弈方战略集的一般转化方法是：采用层次分析法[5]或者直接求解目标对设计变量的偏导数来得到各设计变量对各目标的影响因子矩阵，再对影响因子矩阵进行模糊分类得到其等价矩阵。层次分析法受主观影响较大；直接求解偏导数只能适用于目标函数可导的情况,适用范围小。

因此，本文将均匀设计试验法应用于机械产品多目标优化设计博弈分析的博弈方战略集中,采用均匀设计试验法得到各设计变量对目标的影响因子指标，然后依据模糊聚类法对设计变量进行聚类，最终得到各博弈方的战略集。该方法弥补了现有方法的不足，且不要求目标函数和各约束连续可导，可用来分析离散优化问题，扩大了方法的适用范围。

1　博弈战略集的划分数据基础

1.1机械产品多目标优化的博弈描述

对于一个工程实际问题,目标函数、设计变量和约束条件都确定以后,其最优化数学模型基本确定，多目标优化设计问题的数学模型一般表示为[6]:

minF(X)=(f1(X),f2(X),…,fm(X))

s.t.ai≤xi≤bii=1,2,…,n

hl(X)=0l=1,2,…,p

gk(X)≤0k=1,2,…,q

式中,X为设计变量，X=(x1,x2,…,xn);ai、bi为设计变量xi的下限和上限;n为设计变量的个数;m为优化目标的个数;fm(X)为第m个子目标；p为等式约束的个数;q为不等式约束的个数。

对于n个博弈方的博弈可以表示如下[7]:①有限集P表示博弈方；②Si={s1,s2,…,sm}表示博弈方i的战略集；③S={S1,S2,…,Sn}为所有博弈方的战略空间;④收益函数U为所有博弈方战略效用到实数空间的一个函数映射。因此,可以用G={P,S,U}来表示该博弈。

1.2基于均匀设计、回归分析和F检验的数据分析

要采用均匀设计试验法[8]得到各设计变量对目标的影响因子指标,首先要根据试验目的确定试验指标，然后选择试验因素水平和均匀设计表，制定试验方案,对试验结果进行回归分析和检验。

均匀设计的关键是要建立多因素的回归模型。回归分析统计分析方法可以定量地分析多种变量的相互依赖关系。通过自变量和因变量的回归模型可以对设计变量进行重要性分析，可以估算新型条件下的试验结果，还可以对已有结果进行优化。若设计试验有m个因素，优化目标y关于因素集X的二次多项式回归模型为[9]

其中,β0、βi、βi i、βi j为回归系数;ε为随机误差。

通过F检验可以对均匀设计试验进行检验。F检验服从F分布，可以用来检验均数差别的显著性,分析多个因素的相互作用大小以及分离各个因素,检验方差齐性等[10]。

2　结合模糊聚类和合作竞争博弈分析方法

2.1模糊聚类方法

模糊聚类的数学模型如下:

n个样本数据集矢量X=(x1,x2,…,xn)聚合为m个类别,模糊聚类矩阵U=[uj f]m×n,其中uj f代表该样本xf对第j个类别的同意度。通常，最高的同意度决定了该样本应该属于哪一类。

基于模糊等价关系的模糊聚类法，其传递闭包方法一般是：建立数据矩阵并将数据标准化，进而建立模糊相似矩阵，再传递闭包聚类。

2.2合作竞争博弈优化

结合模糊聚类和合作竞争博弈分析方法步骤如下：

(1)建立多目标问题的数学模型，确立多目标优化问题的设计变量、目标函数和约束条件，通过均匀设计试验和回归分析得到各设计变量对各设计目标的影响因子矩阵，并进行传递闭包转化，成功转化多目标问题为博弈优化问题，求得策略集组合S={S1,S2,…,Sm}。

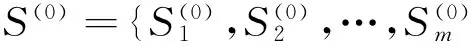
i,j=1,2,…,m

3　减速器高速级传动的优化设计

以带式输送机减速器的高速级齿轮传动为例进行优化设计。已知输出功率P1=10 kW,小齿轮转速为n1=960 r/min,传动比i=3.2(齿数比u=i)。驱动方式为电动机驱动,假设每年365个工作日,工作15年，两班倒。假设工况是带式输送机工作平稳，转向保持不变。

减速器的三个设计目标为齿轮啮合重合度(f1)、齿轮体积(f2)、接触疲劳安全度(f3,即接触疲劳极限应力与接触疲劳许用应力之比)。理想的状态是通过优化设计变量，使得重合度达到最大，同时减小体积并使安全度尽可能大。4个设计变量分别为模数x1、主动轮齿数x2、载荷系数x3、齿宽系数x4。因此，选用均匀设计试验U7(74),对应因素水平得到均匀试验结果，如表1所示。对均匀设计试验进行回归分析计算，回归分析结果中，目标函数f1、f2、f3的回归分析F值分别为F1=29.7220，F2=111.4113，F3=48.2889，查F检验表，得到F(4,3)=9.12，回归分析F值结果与检验表数据对比，F1>9.12,F2>9.12,F3>9.12,因此均匀试验设计结果可靠，由此可以得到减速器4个设计变量对3个目标函数的回归分析的系数结果矩阵为

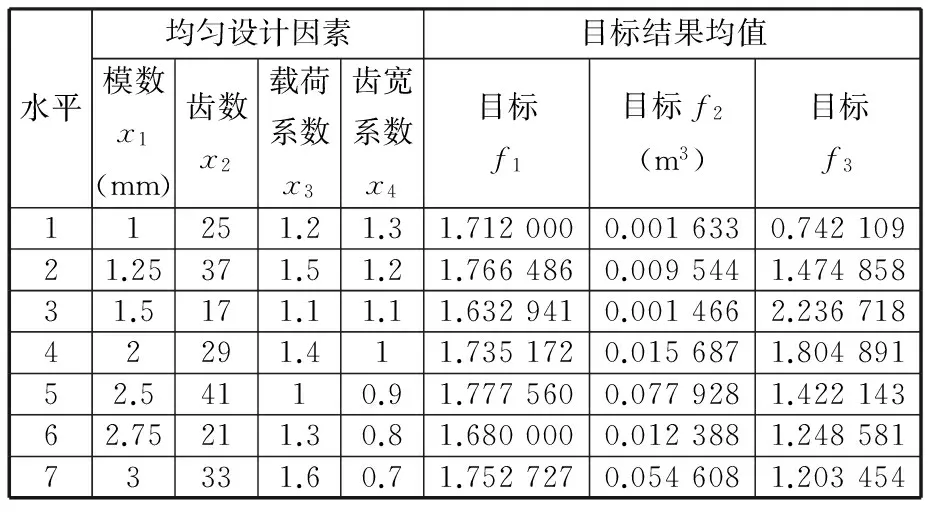
表1　均匀设计试验结果

由得到的回归系数矩阵，可以得到模糊相似矩阵为

用MATLAB编程，根据模糊聚类传递闭包的原则可以得到，减速器模糊聚类的传递闭包矩阵为

由传递闭包矩阵可以看出,令置信度λ=0.99,模糊聚类矩阵为

因此，可以对4个设计变量聚类为：{1,2}、{3}、{4},应用本文的方法，得到优化结果如表2所示。合作竞争博弈优化迭代的过程设计变量x1、x2、x3、x4如图1所示，目标f1、f2、f3的博弈迭代结果如图2所示。

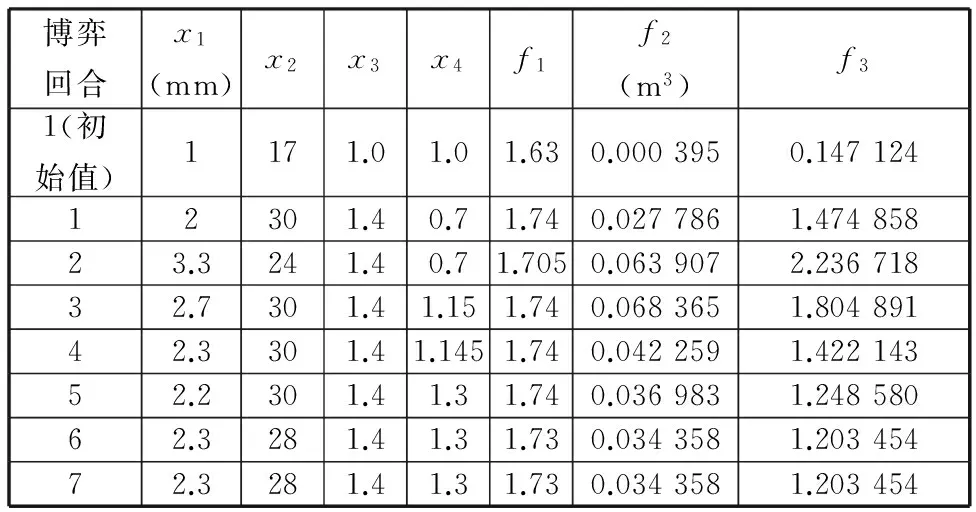
表2　减速器博弈优化结果

图1　4个设计变量的合作竞争博弈优化迭代过程

4　计算结果比较及结论

本文设计得到的结果与传统的减速器设计结果[11]进行对比,如表3所示。基于权重的多目标优化方法中，对于三个目标权重分别为0.333，编程求得的优化结果见表4。该优化结果表明，本文的方法在齿面接触、齿根弯曲强度等多种约束条件下，通过增大齿数，增加了减速器传动的重合度，使得传动的时候啮合更平稳，减少了减速器的跑偏、漏料以及异常噪声等现象。增大齿数的同时，减少模数，减小了齿轮加工的时候金属的切削量，节省了制造费用，提高了减速器的工程经济性能。降低齿宽系数使得体积减少很多，但是因为齿数的增大，齿宽影响不大，不影响齿轮的承载能力。

表3　本文设计和传统优化设计结果对比

表4　本文设计和基于权重的多目标优化结果对比

本文通过均匀设计试验得到各设计变量对所有目标的影响因子指标，再利用模糊聚类进行分类，实现各博弈方战略集的划分，将多目标优化问题转化为博弈问题;在此基础上提出一种机械产品多目标优化设计方法(即多目标优化设计博弈分析方法),算例结果验证了该方法的可行性。与传统的优化设计方法相比，该方法不需要人为确定各目标的权重，可以用于离散问题的优化，计算效率高，具有工程应用价值。

[1]唐焕文,秦学志.实用最优化方法[M].大连:大连理工大学出版社, 2004.

[2]Sawaragi Y,Nakayama H,Tanino T.Theory of Multi-objective Optimization[M].New York:Academic Press,1985.

[3]谢能刚,方浩,包家汉,等.博弈决策分析在补偿滑轮组变幅机构多目标设计中的应用[J].机械强度,2005,27(2):202-206.

Xie Nenggang,Fan Hao,Bao Jiahan,et al.Game Analysis of Multi-objective Design on Iuff Mechanism of Compensative Sheave Block[J].Journal of Mechanical Strength,2005,27(2):202-206.

[4]Bao J H,Xie N G,Cen Y W,et al.Multi-objective Optimization Design of Passive Suspension Parameters Based on Collusion Cooperation Game Theory[C]//2010 8th World Congress on Intelligent Control and Automation,WCICA 2010.Jinan,2010:118-125.

[5]刘亚相,孙洪罡,王丽波,等.多目标博弈的模糊求解法[J].西北农林科技大学学报(自然科学版),2004,32(10):149-152.

Liu Yaxiang,Sun Honggang,Wang Libo,et al.Fuzzy Solution in Multiobjective Games[J].Journal of Northwest Sci-Tech University of Agriculture and Forestry,2004,32(10):149-152.

[6]方世杰,綦耀光.机械优化设计[M].北京:机械工业出版社,2003.

[7]Wu Jie.Cooperation with Competitors and Product Innovation:Moderating Effects of Technological Capability and Alliances with Universities[J],Industrial Marketing Management,2014,43(2):199-209.

[8]刘永才.均匀设计及其应用[J].战术导弹技术,2002(1):58-61.

Liu Yongcai.Uniform Design and Its Application[J].Tactical Missile Technology,2002(1):58-61.

[9]Lulic H,Civic A,Pasic M,et al.Optimization of Thermal Insulation and Regression Analysis of Fuel Consumption[J].Procedia Engineering,2014,69(3):902-910.[10]韦艳玲.基于F检验的模糊聚类小额农贷款信用风险预测[J].安徽农业科学,2011,39(1):565-566,597.

Wei Yanling.Prediction of Credit Risk of Micro-loans to Farmer by Using Fuzzy Clustering Based onFTest[J].Journal to Anhui Agricultural Sciences,2011，39(1):565-566.597.

[11]杨可桢,程光蕴,李仲生.机械设计基础[M].北京:高等教育出版社,2006.

(编辑王旻玥)

Optimization Method Based on Fuzzy Clustering and Cooperative Competition Game

Chen Jiaming1Song Xiaowen2Xu Hao2

1.Hangzhou Vocationaland Technical College,Hangzhou,310000 2.Zhejiang University,Hangzhou,310027

Aiming at the difficulty of transforming multi-objective optimization problem to game problem which was about determining the strategy set for each partition of game players,a multi-objective optimization method was proposed by using uniform design experimentation,regression analysis and F test statistic to obtain data bases for fuzzy clustering and combining cooperative competition game.Taking reducer design optimization as an example,performance of the method was analyzed and verified.Compared with the traditional single-objective optimization method,the experimental results show that the multi-objective method has fast convergence rate and high computational efficiency,and it is unneccessary to determine the weight of each target,which has engineering application values.

fuzzy clustering;cooperative competition game;uniform design;regression analysis

2015-04-02

TG122DOI：10.3969/j.issn.1004-132X.2015.16.009

陈加明,男,1970年生。杭州职业技术学院友嘉机电学院副教授。主要研究方向为模具设计、模具CAD/CAM等。获国家教学成果2等奖1项，浙江省教学成果1等奖1项，发表论文10余篇。宋小文,女,1967年生。浙江大学机械工程学院副教授。徐浩,女,1990年生。浙江大学机械工程学院硕士研究生。