隐式功能函数结构体可靠性拓扑优化

吴劲松　周金宇

江苏理工学院常州市装备再制造工程重点实验室,常州,213001

隐式功能函数结构体可靠性拓扑优化

吴劲松周金宇

江苏理工学院常州市装备再制造工程重点实验室,常州,213001

考虑工程实际中外载荷、材料属性等的随机不确定性对结构安全性的影响，研究了具有结构位移可靠性约束的拓扑优化设计。建立以柔度最小为目标、以单元相对密度为变量、具有材料体积分数约束和结构位移可靠性约束的拓扑优化数学模型；针对运用有限元数值计算方法时结构功能函数为隐式的情况，运用响应面法近似逼近结构真实的功能函数；利用简便高效的一次二阶矩法计算结构位移可靠度;采用内循环为确定性的拓扑优化、外循环控制结构材料体积分数的策略对连续体结构进行可靠性拓扑优化设计。通过两个算例与确定性拓扑优化结果进行比较,结果表明所提设计方法是高效可行的。

可靠性;拓扑优化;隐式功能函数;响应面法

0　引言

连续体结构拓扑优化一直是结构设计中的难点和热点问题。目前对连续体结构拓扑优化的研究已经有了长足的发展，形成了均匀化方法[1]、变密度法[2]、渐进结构优化法、双向渐进结构优化方法[3-4]以及水平集法[5]等拓扑优化方法。当前对拓扑优化的研究大多是基于确定性假设，没有考虑实际工程中载荷、材料属性、结构尺寸等的不确定性。由于没有考虑这些不确定性因素对结构的影响，所以确定性的拓扑优化得到的结构安全裕度较低，对于一些对随机变量敏感的问题，确定性拓扑优化很难保证结构的可靠性和安全性。

在拓扑优化过程中将载荷、材料属性等参数视为随机变量，将结构的可靠性作为拓扑优化问题的约束条件之一，研究结构的可靠性拓扑优化，在求解算法中将结构可靠性理论和拓扑优化技术进行有机融合，由于定量计入了影响结构性能的各种不确定因素，因此结构可靠性拓扑优化设计能在安全性和经济性之间达到最佳平衡，从而有效克服了传统结构优化设计的不足，使设计结果更趋合理[6]。近年来可靠性拓扑优化的研究引起了许多学者的重视,文献[7-8]运用一种启发式策略先对随机变量进行修正使其满足结构的可靠性要求，再用修正后的随机变量进行确定性的拓扑优化研究；文献[9-10]分别利用渐进结构优化法和双向渐进结构优化法结合响应面法对具有可靠性约束的拓扑优化进行了讨论；文献[11-12]通过随机有限元法将结构的拓扑优化视为一种对单元的模式识别，研究了随机变量服从正态分布和非正态分布的连续体可靠性拓扑优化问题。迄今为止,对连续体可靠性拓扑优化研究大都是将可靠性分析和拓扑优化同时进行，每步拓扑优化迭代都要计算一次结构的可靠性，存在计算量大、计算效率低和精度难以保证等问题。同时，在可靠性分析过程中,对于结构功能函数为隐式时如何计算结构可靠性也没有做详细的阐述。

本文在传统的拓扑优化设计研究的基础上，基于变密度法建立了具有结构位移可靠性约束的拓扑优化模型，利用响应面法对隐式的结构功能函数近似逼近，再进一步算得结构的位移可靠性指标。将可靠性分析和拓扑优化设计分开进行研究，通过内循环是确定性拓扑优化、外循环是控制材料体积分数大小这种内外循环策略实现对结构的可靠性拓扑优化研究。最后通过两个算例来验证文中方法的可行性。

1　可靠性拓扑优化基本模型

拓扑优化就是在给定的设计区域内寻求满足约束条件下的最优结构传力路径和材料分布。经典的拓扑优化设计是在给定的材料体积分数下寻求具有柔度最小的最优拓扑结构，其基于变密度法的数学模型为[13]

(1)

式中,xi为材料单元的相对密度,即设计变量;ui为材料单元位移列向量;k0为材料密度为“1”的单元刚度矩阵;xmin为最小材料单元密度,通常取为0.01;vi为材料单元相对体积;p为惩罚因子;C为结构整体的柔度值;K为整体结构刚度矩阵;U为整体位移列向量;F为外载荷向量;V为整体结构体积;V*为优化后的结构体积;f为给定的材料体积分数。

由式(1)可以看出：经典的拓扑优化寻求的是在给定材料体积分数下具有柔度最小即刚度最大的最优结构。在结构设计中我们更多时候关心的是结构在外载荷作用下最大位移是否满足设计要求。经典的确定性拓扑优化得到的优化结构仅仅是满足刚度最大，至于结构最大位移、最大应力等是否满足设计要求都无法得知。此外，实际工程中的载荷、材料性能、结构尺寸等都是不确定的。因此，单纯研究确定性拓扑优化所得到的结构显然会存在很多缺陷，更加没有可靠性保障。现考虑与结构刚度密切相关的结构位移可靠性，建立基于变密度法具有位移可靠性约束的拓扑优化数学模型如下：

(2)

式中,P[g(X)=δ*-δi≥0]>P*为结构的可靠性约束;P*为结构允许可靠度;δi为单元的位移;δ*为结构许用的最大位移。

2　隐式功能函数的近似逼近

连续体可靠性拓扑优化设计的可靠性约束为

P[g(X)=δ*-δi≥0]>P*

(3)

其中g(X)=δ*-δi≥0为结构安全状态下的功能函数。对式(3)的求解需要计算每个单元的可靠性。如果结构位移最大的单元都能满足

P[g(X)=δ*-max{δ(i)|i=1,2,…,n}≥0]>P*

(4)

那么整个结构就一定能满足可靠性要求,所以问题就可以简化成只需计算位移最大的单元的可靠性约束。假设随机变量都服从正态分布，结构处在安全域内的功能函数为

g(X)=δ*-max{δ(i)|i=1,2,…,n}>0

(5)

g(X)>0的概率为

P[g(X)>0]=1-P[g(X)≤0]=

(6)

式中,Φ(·)表示标准正态变量的累积分布函数;ug和σg分别表示结构功能函数的均值和标准差。

式(6)表明,结构可靠度和可靠性指标之间是一一对应的关系。根据结构可靠性指标的定义,β可表示为在标准化正态空间S中从坐标原点到失效面的最短距离,即

(7)

其中，si是将随机变量标准化后的标准正态变量。随机变量标准化方程为

(8)

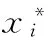
由以上分析可以看出,只要知道结构的功能函数,利用简单的一次二阶矩法就可以很方便地得到结构的可靠度,但此处结构功能函数式(5)是一个隐式,无法得知它的准确表达式，这就给一次二阶矩法的应用带来了巨大困难。针对这种情况,可采用响应面法求解。

响应面法通过合理选取试验点和迭代策略来保证多项式函数能够在失效概率上收敛于真实的隐式极限状态函数的失效概率。用于拟合的多项式有很多种，其中二次不含交叉项的响应面由于结构简单、运算量小、精度相对较高被广泛应用。二次不含交叉项的响应面的功能函数为

(9)

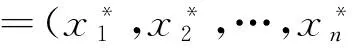
(10)

图1　试验点选取示意图

利用最小二乘法求得线性响应面的待定系数

b=(ATA)-1ATy

(11)

其中，A是由2n+1个试验点xl1,xl2,…,xln(l=1,2,…2n+1)组成的(2n+1)×(2n+1)阶样本矩阵:

A=

(12)

(13)

经过一次迭代可得近似功能函数,如图2a所示;经过多次迭代则不断接近真实功能函数，如图2b所示,直到相邻两次迭代算得的可靠性指标满足|βj-βj-1|<0.001,则停止迭代,输出结果β。

(a)一次迭代(b)多次迭代图2　响应面法获取近似功能函数

3　高效可靠性拓扑优化流程

可靠性拓扑优化研究的难点是如何将可靠性分析和拓扑优化简单高效地结合在一起，克服计算量大的困难并且保证所需精度。在当前的求解方法中,可靠性分析和结构拓扑优化是在同一迭代循环内完成的，即首先通过相应优化准则对结构进行优化，每次迭代后再利用有限元分析得到结构的位移和应力，然后进行可靠性分析，最后判断是否满足可靠性约束和其他约束要求。如果不满足, 再重新优化直到满足设计约束[14-16]。但每次迭代结构的拓扑形状都发生变化，需要重新计算结构可靠性。同时，由于变化的无规律性，导致无法得知结构功能函数的表达式，给可靠性计算带来困难。所以将可靠性分析放在拓扑优化过程中，存在重复计算可靠性的问题，增加了求解计算量。

拓扑优化实质就是通过一定的方法逐渐去除对结构性能贡献小的材料,保留对结构性能贡献大的材料。材料去除得越多,对应确定性拓扑优化即式(1)中的体积分数f越小,经过拓扑优化得到的结构只是满足刚度最大，是否能满足位移可靠性的约束则需要进一步验证。可以明确的是,f越大,结构受载后的最大位移肯定越小，对应的位移可靠性也越高。去除的材料过多，结构的可靠性就无法得到保障；去除的材料过少，结构又过于保守,达不到优化的目的[17]。

因此,通过控制材料体积分数，找到合适的体积分数f能使结构安全性和经济性达到最佳平衡，就能解决可靠性拓扑优化问题。综上所述，可以利用内外循环的策略，内循环为确定性拓扑优化,外循环为控制材料体积分数f的大小。首先给定一个初始体积分数f，进行确定性拓扑优化即内循环，然后对优化后的结构进行有限元分析，并结合响应面法得到结构的功能函数，最后利用式(7)算出可靠性指标β。如果可靠性指标小于给定的指标β<β*,则说明去除材料过多,这时增大体积分数f，返回确定性拓扑优化前的模型，再次运行内循环，直到β≥β*,再进一步判断是否满足可靠性指标收敛准则:

|β-β*|≤ξ

(14)

如果不满足则说明结构还有优化空间,这时再减小体积分数f运行内循环。通过二分法增大或者减小材料体积分数直到满足式(14)为止，整个优化流程如图3所示。

图3　可靠性拓扑优化流程框图

4　算例

4.1算例一

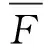
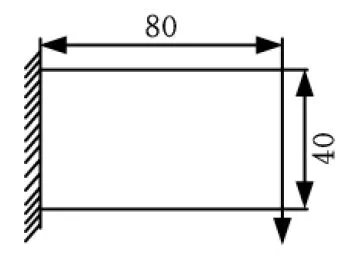
图4　悬臂梁的设计域

图5　不考虑可靠性的优化结果

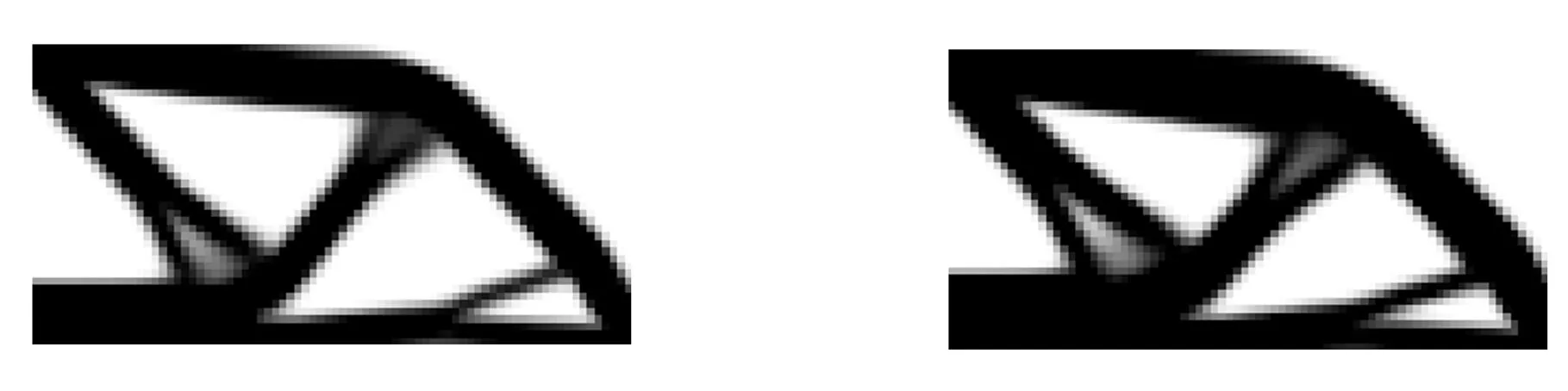
(a)β=4.0(b)β=2.0图6　考虑位移可靠性约束的优化结果

图7　算例一迭代历程

4.2算例二

图8　初始的设计域

图9　不考虑可靠性的优化结果

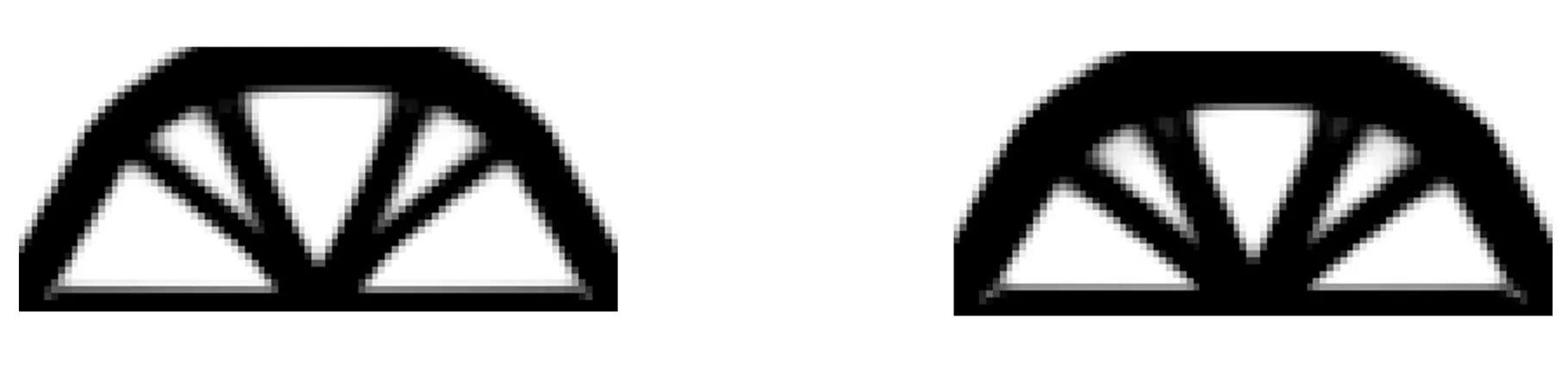
(a)β=4.0(b)β=2.0图10　考虑位移可靠性约束的优化结果

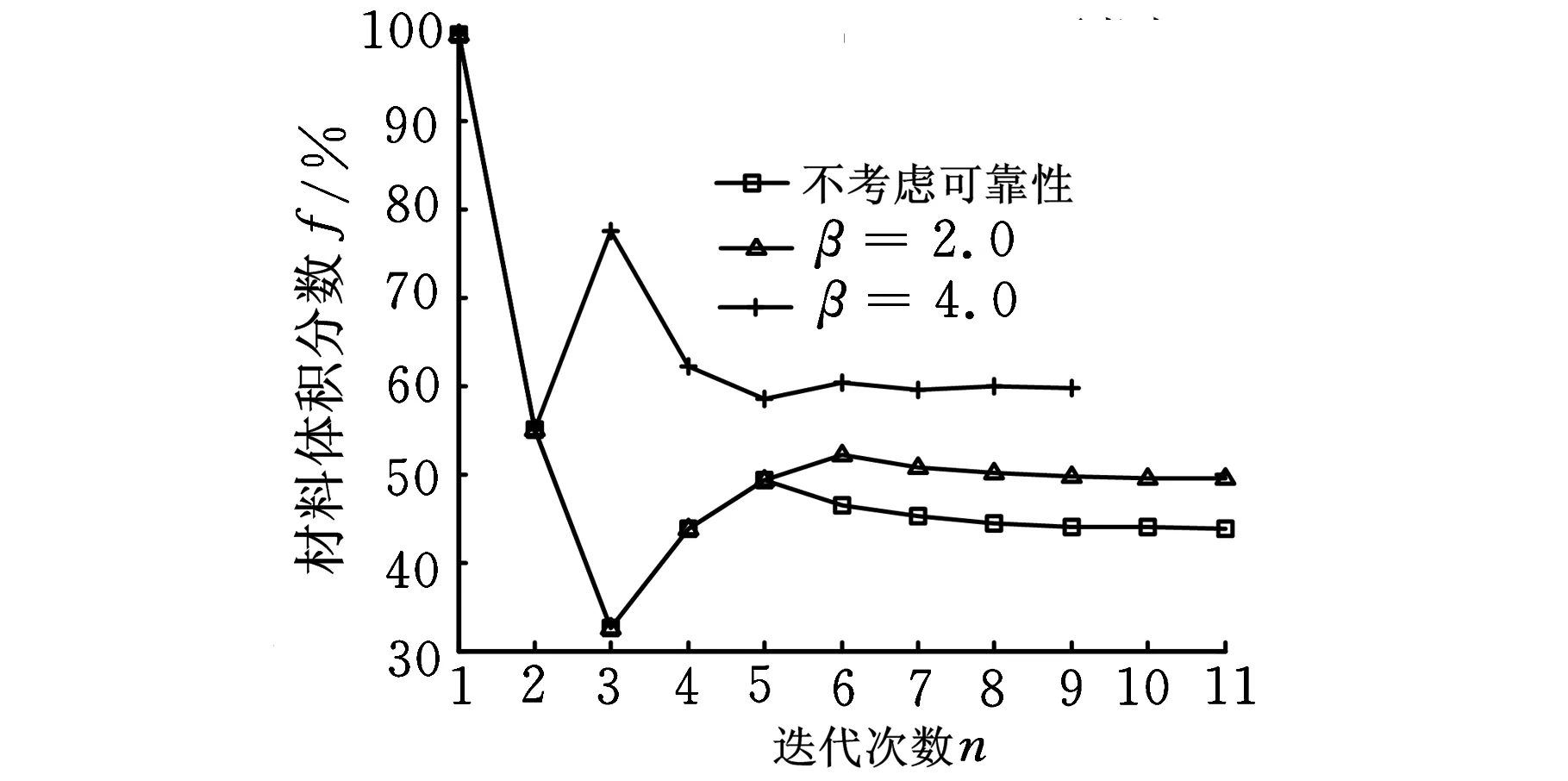
图11　算例二迭代历程

表1所示为算例一、算例二分别考虑可靠性和不考虑可靠性的优化结果数据，可以看出，考虑可靠性约束优化结构的最大位移明显小于不考虑可靠性约束结构的最大位移，因此考虑可靠性所得结构更加合理。同时，由于定量考虑了结构的可靠性，所以结构不仅能满足刚度最大而且有一定的可靠性保证，从而实现了结构经济性和安全性的最佳平衡。

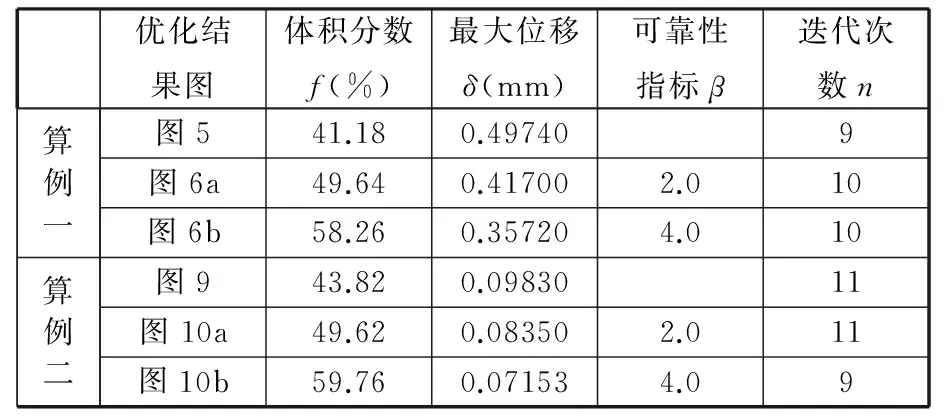
表1　优化结果对照表

5　结论

(1)利用响应面法近似逼近结构的隐式功能函数，极大简化了因结构功能函数为隐式给可靠性分析带来的困难。

(2)采用内外循环的策略，将可靠性分析和拓扑优化分开进行，避免了在拓扑优化过程中每步迭代都计算结构可靠性，而只需在拓扑优化结束时计算一次结构可靠性指标，极大减小了计算量同时提高了计算效率。

(3)算例一、算例二的分析结果表明:可靠性拓扑优化与确定性的拓扑优化相比，结构的体积分数仅有少量增加就能获得较大的可靠度增长。该方法对于解决连续体可靠性拓扑优化是简易可行的，可为解决工程实际的结构可靠性拓扑优化设计提供新思路和实用方法。

[1]Bendsoe M P，Kikuchi N.Generating Optimal Topologies in Structural Design Using a Homogenization Method[J].Computer Methods in Applied Mechanics and Engineering,1988,71(1):197-224．

[2]Bendsoe M P,Sigmund O.Material Interpolation Schemes in Topology Optimization[J].Archive of Applied Mechanics,1999,69(9):635-654．

[3]Xie Y M,Steven G P.A Simple Evolutionary Procedure for Structural Optimization[J].Computers and Structures,1993,49(5):885-896．

[4]Querin O M,Yong V,Steven G P,et al.Computational Efficiency and Validation of Bi-directional Evolutionary Structural Optimization[J].Computer Methods in Applied Mechanics and Engineering,2001,189(2)：559-573．

[5]Sethian J A,Wiegmann A.Structural Boundary Design via Level Set and Immersed Interface Methods[J].Journal for Numerical Method in Engineering,2003,57(8):1177-1196．

[6]刘国梁,陈建军,马洪波.一种基于非概率可靠性的结构水平集拓扑优化[J].工程力学,2012,29(6)：58-62．

Liu Guoliang,Chen Jianjun,Ma Hongbo.Structural Topology Optimization for Non-probability Reliability in Level Set Method[J].Engineering Mechanics,2012,29(6):58-62.

[7]Kharmanda G,Olhohoff N,Mohamed A,et al.Reliability-based Topology Optimization[J].Structural and Multidisciplinary Optimization,2004,26(5)：295-307．

[8]邝泳聪，欧阳高飞，张宪民． 基于可靠性的连续体结构拓扑优化设计[J]． 机械强度，2009，31 (4)：604-608．Kuang Yongcong,Ouyang Gaofei,Zhang Xianmin.Structural Topology Optimization of Continuous Structures Based on Reliability[J].Journal of Mechanical Strength,2009,31(4):604-608.

[9]Kwang S Y,Eom Y S,Park J Y,et al.Reliability-based Topology Optimization Using Successive Standard Response Surface Method[J].Finite Element in Analysis and Design,2011,47(7):843-849.

[10]Kwang S Y,Yong S E,Jae Y P,et al.Reliability-based Topology Optimization Using a Standard Response Surface Method for Three-dimensional Structures[J].Structural and Multidisciplinary Optimization,2011,43(2):287-295．

[11]李景奎，张义民．正态分布连续体结构可靠性拓扑优化设计[J].东北大学学报,2011,32(9):1303-1309．

Li Jingkui,Zhang Yimin.Reliability-based Topology Optimization Design of Normal Distribution Continuum Structure[J].Journal of Northeaster University,2011,32(9):1303-1309．

[12]李景奎,张义民.非正态分布连续体结构可靠性拓扑优化设计[J].机械工程学报,2012,48(3):153-158,Li Jingkui,Zhang Yimin.The Reliability-based Topology Optimization Design of Continuum Structure with Abnormal Distribution[J].Journal of Mechanical Engineering,2012,48(3):153-158．

[13]李好.基于变密度法的连续体结构拓扑优化方法研究[D].武汉:华中科技大学,2011.

[14]Chwail K,Semyung W.Reliability-based Topology Optimization with Uncertainties[J].Journal of Mechanical Science and Technology,2006,20(4):494-504．

[15]Maute K,Frangopol D M.Reliability-based Design of MEMS Mechanisms by Topology Optimization[J].Computers and Structures,2003,81(8):813-824．

[16]Seung J H,Seonho C.Reliability-based Topology Optimization of Geometrically Nonlinear Structures with Loading and Material Uncertainties[J].Finite Elements in Analysis and Design,2004,41(3):311-331．

[17]Zhang Bin,Wang X J,Sun X Y.Structural Topology Optimization Considering Stress and Reliability Constraints[J].Metalurgia International,2014,ⅪⅩ(2):59-63．

(编辑苏卫国)

Reliability-based Topology Optimization of Implicit Performance Function Structure

Wu JinsongZhou Jinyu

Changzhou Key Laboratory of Equipment Remanufacturing Engineering, Jiangsu University of Technology,Changzhou,Jiangsu,213001

Considering the impacts of uncertain factors such as external loading,material property etc. on structural safety in engineering practice,the topology optimization design with the structural displacement reliability constrain was discussed.A mathematical of topology optimization was developed,where the minimization of compliance was taken as objective function,the relative densities of elements were taken as design variables,the material volume fraction and structural displacement reliability were taken as constraints.The response surface method was implemented to approximately approach its real performance function, for the situation that the structural performance function was implicit by using finite element numerical method.Then,the simple and efficient first order second moment method was used to obtain the structural displacement reliability.The strategy that inner loop was the deterministic topology optimization and the outer loop was to control the material volume fraction was implemented to carry out the reliability-based topology optimization of continuum structure.Finally,two numerical examples were given to be compared with the results of deterministic topology optimization showing that the design method is efficient and feasible.

reliability;topology optimization;implicit performance function;response surface method

2015-03-02

国家自然科学基金资助项目(51275221);江苏省产学研联合创新资金资助项目(BY2014038-04)

TB114;H122DOI：10.3969/j.issn.1004-132X.2015.16.013

吴劲松，男，1989年生。江苏理工学院机械工程学院硕士研究生。研究方向为先进再制造技术与装备。周金宇，男，1973年生。江苏理工学院机械工程学院教授、博士、硕士研究生导师。