超声导波评价长骨骨折的仿体实验研究∗
2015-10-28胡时晓许凯亮他得安
胡时晓 许凯亮 他得安
(复旦大学电子工程系 上海 200433)
⋄研究报告⋄
超声导波评价长骨骨折的仿体实验研究∗
胡时晓许凯亮他得安†
(复旦大学电子工程系上海200433)
定量超声评价长骨骨折已成为近年来的研究热点之一,超声导波模式转换理论可被应用于长骨骨折状况的评价。采用三维时域有限差分法分析骨折长骨中导波模式转换的基本规律,提取模式转换定量评价参数;进而结合亚克力管仿体实验,分析不同裂纹程度下导波模式的转换情况。仿真与仿体实验表明,导波模式能量参数与裂纹程度具有很好的相关性,可用于评价长骨骨折状况。
长骨骨折,超声导波,模式转换,三维时域有限差分
1 引言
骨折是一种日常多发疾病,临床表现为在外伤或病理等因素作用下所致的骨缺失性病症[1]。及时发现愈合障碍以确保骨折正常愈合是骨折慢性治疗的关键,准确诊断与动态监测则是给予合理治疗的前提与基础。
现有的X线片、CT,MRI、放射性核素等方法,虽在骨折诊断中获得了广泛的应用,但因检查费用以及辐射损伤等原因均不适于多次性的跟踪检查,也无法满足监测骨折愈合的临床需要[2]。基于超声导波的骨折愈合监测技术除具备传统超声技术的费用低、无电离辐射、简便、速度快、可携带以及适于普查应用等优点外,还可反映长骨皮质骨几何形状(包括厚度、截面形状)与材料特性(包括骨密度、微孔率和杨氏模量)等信息[2-4]。因此,应用超声导波评价长骨状况已成为当前骨超声研究中极具前景的课题[5-13]。
近年来,超声导波已被广泛用于工业管道、板材等的无损检测与评价[14-15]。超声导波在缺陷处的模式转换现象,已被研究者广泛重视并应用于缺陷定位与评价[16]。长骨骨折后,皮质骨骨折线处会产生导波模式转换现象,相关模式参量的研究对骨折裂纹评价具有重要意义。明确提出将超声导波应用于诊断骨折及其愈合过程评价的报道见于2006年,Protopappas等[17]用二维板状结构建模长骨骨折,研究表明,超声Lamb波速度可反映长骨皮质骨软骨组织的生长变化。随后,Protopappas等[18]用三维有限元模型,分析了长骨组织愈合钙化过程对超声导波纵向模式传播的影响。许凯亮等[11]采用边界元法分析了骨折长骨中各纵向导波模式的反射系数与透射系数的变化规律,进而讨论了敏感频率与导波模式。刘洋等[10]提出将非线性与时间反转相结合实现骨裂纹超声成像的方法,并进行了仿真验证。许凯亮等[19]采用时域有限差分仿真法,分析了低频窄带激励下两个基本的导波模式S0与A0在骨折裂纹处的模式转换现象,研究表明两模式间的能量转换参数可用于评价长骨骨折状况。随后,许凯亮等[20]将羊胫骨视为板状模型,实验上初步验证了Lamb波导波模式能量比与裂纹程度具有高度相关性。刘丹等[21]采用低频窄带激励法,从仿真角度初步研究了透射导波模式幅度对骨折裂纹宽度与角度的敏感程度。上述研究表明超声导波极具应用于长骨骨折及愈合评价的潜力。但是,将采用管状结构建模长骨皮质骨,并分析其中柱面纵向导波模式的研究仍有待深入。
本文采用三维时域有限差分法分析纵向导波模式L(0,1),L(0,2)在骨干裂纹处的模式转换基本规律,并结合亚克力管仿体实验,在导波模式分离及模式转换参数提取的基础上,定量评价模式转换程度,最终实现骨折裂纹程度的评估。
2 超声导波理论及模式转换现象
长骨模型如图1所示,根据位移分量的不同,可将柱状导波模式分为三种典型传播模态:纵向模式L(0,m)、扭转模式T(0,m)和弯曲模式F(n,m),m,n=1,2,3,···[8,22-23]。在轴向传播方式相关的导波应用中,因纵向模式的可激发性以及可重复性,采用较为普遍;另外由于对称性,纵向模式又较弯曲模态更易于激发,便于对管状波导进行360°检测与评价[2,23]。本研究中采用轴向传播方式测量长骨骨折状况,因此讨论仅限于纵向模式。
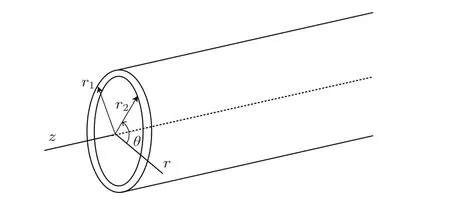
图1 柱坐标下的长骨模型,外半径与内半径分别为r1与r2Fig.1 Long bone model under cylindrical coordinate,outer radius and inner radius are r1and r2respectively
2.2频散曲线
由于亚克力管声学参数与长骨皮质骨较为接近,常被用做长骨超声研究的仿体材料[24-25]。根据导波理论[8],可得内半径为7.5 mm、厚度为2.5 mm的长骨皮质骨(密度为1.5 g/cm3)和亚克力管(密度为1.2 g/cm3)频散曲线如图2所示,纵轴为群速度,横轴为频率与厚度的乘积,简称频厚积。
如图2所示,下标a标注了亚克力管中的低阶导波模式群速度的理论曲线,由虚线表示;下标b标注了长骨中的低阶导波模式群速度的理论曲线,由实线表示。应用轴向传输激励的方法不易于接收到F模态,但可在长骨中接收到以纵向模态为主的导波信号[8]。由图2可得,当频厚积小于L(0,3)的截止频厚时,将主要获得两个最低阶的导波模式L(0,1)与L(0,2)[9]。在D1区间中,长骨导波模式Lb(0,1)与Lb(0,2)群速度差异明显,有助于模式波包的分离。相类似的,亚克力管中的La(0,1)与La(0,2)模式在D2区间内也较易识别与分离。

图2 长骨皮质骨频散曲线(实线)与亚克力管频散曲线(虚线)对比图Fig.2 Comparison of frequency dispersion curve between cortical bone(solid line)and acrylic tube(dotted line)
2.3模式转换现象
导波的产生是由横波、纵波在边界处的转换与叠加造成的,因而不同的边界条件也影响着导波的传播特性,并导致截然不同的导波模式能量分布。利用导波对边界条件的敏感特性来评价波导材料的内、外缺陷一直是学界讨论的热点。此类研究主要方法为分析各类缺陷所对应的导波模式转换规律与参数,达到评价波导材料损伤状况的目的。
可见,慧览也是一位游历十分丰富的高僧,他曾去罽宾习禅求法,后返回于阗弘法。又经吐谷浑到内地巴蜀,受到吐谷浑主慕延和世子琼的礼遇,为他在蜀地立左军寺。他后来还是离开巴蜀,来到岭南,驻锡罗浮山天宫寺。在崇佛的宋文帝盛情邀请下,来到京师建业,驻锡钟山定林寺。宋武帝继位,修建中兴寺,下令慧览移住其中。宋武帝大明年间(456—464),慧览圆寂。
管状骨折长骨三维模型如图3(a)所示,其外表面有一条环切裂纹,裂纹宽度为w,深度为d,管外半径、内半径分别为r1与r2。图3(b)为图3(a)中阴影部分截面示意图。环形裂纹到发射探头和接收探头的距离分别为x1,x2。
在低频厚积下,采用轴向激励法可主要激发出两个最低阶的纵向导波模式L(0,1)与L(0,2)。已有研究表明[19],低阶纵向导波模式A0和S0在骨折裂纹处能够发生模式转换,而导波模式L(0,1)与L(0,2)也会发生类似的模式转换现象。如图3(b)所示,原来的L(0,1)转换而来的L(0,2)模式和由L(0,2)转换而来的L(0,1)模式,图中分别用L(0,2)L(0,1)与L(0,1)L(0,2)表示。因此,裂纹长骨中,接收探头可同时测得原始模式L(0,1),L(0,2)与转换模式L(0,1)L(0,2),L(0,2)L(0,1)所构成的混合信号。
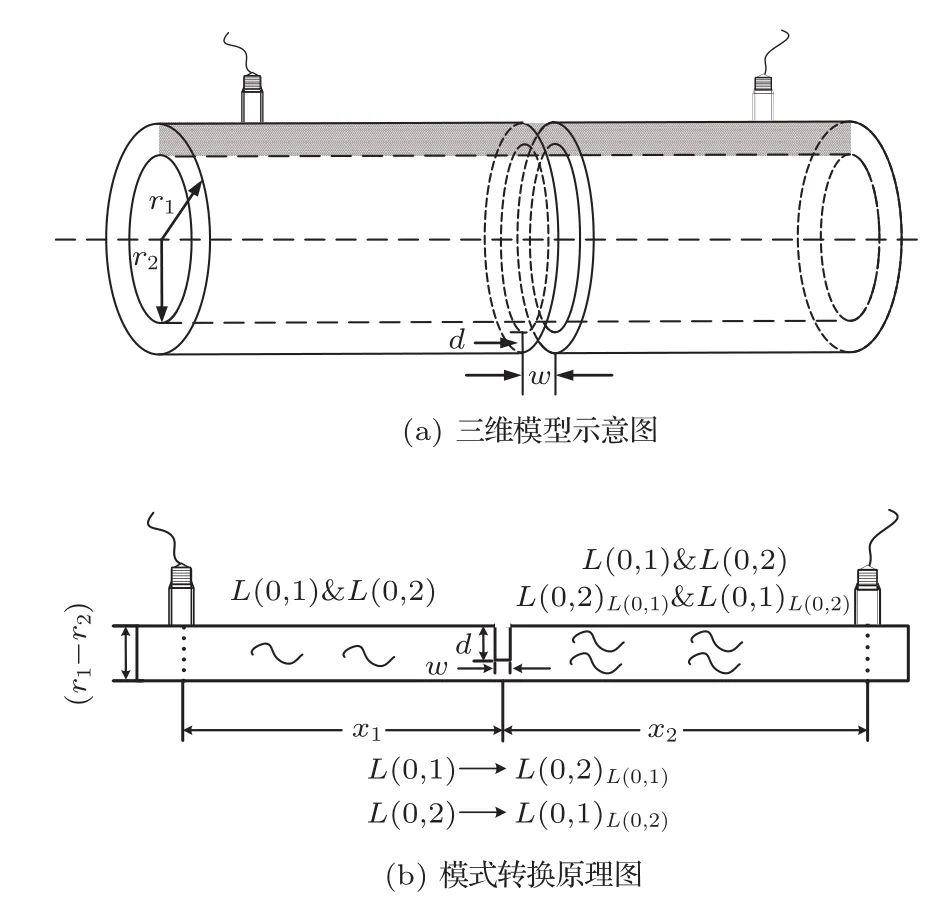
图3 骨折长骨示意图Fig.3 Schematic diagram of long bone fracture
设L(0,1),L(0,2)速度分别为V1,V2,则转换模式L(0,2)L(0,1)与L(0,1)L(0,2)到达接收探头时间T21,T12可表示为[14,20]
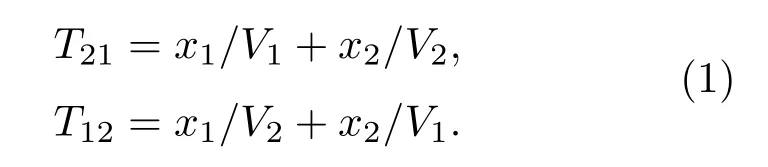
则L(0,2)L(0,1),L(0,1)L(0,2)模式的观测速度可表示为[14,20]

在低频厚积处有V1< V2,则V1< V12,V21<V2。特别的,当x1=x2时有[14,20]

式(3)表明,当长骨中部发生骨折时,转换模式L(0,1)L(0,2),L(0,2)L(0,1)波包速度较为接近。
3 仿真原理和实验
3.1仿真模型
本文采用三维时域有限差分法建模长骨仿真模型[26-27],该模型如图3所示。仿真所用的管状长骨结构模型与图3相同,选用材料为亚克力管,其中密度为1.2 g/cm3,纵波速度为2738 m/s,横波速度为1380 m/s,仿真的采样频率为30 MHz,选用的激励信号为四周期高斯包络的正弦信号,其中心频率为200 kHz,-3 dB带宽约为95 kHz。长骨内外表面采用应力自由边界条件,两端设置完全匹配层吸收边界,以消除反射回波干扰,环切裂纹被置于发射与接收探头中间,发射和接收探头之间的距离定为100 mm。亚克力管外半径为10 mm,内半径为7 mm,7.5 mm,8.2 mm,对应了管壁厚度为3 mm,2.5 mm,1.8 mm三种情况。为了研究不同裂纹程度对于导波模式转换的影响,分别考虑了完好以及环刻凹槽深度在20%、40%、60%、80%的情况。由于微裂纹的宽度对接收信号影响较小,因此本文只研究环刻凹槽宽度为1 mm的情况。
3.2实验方法
选用亚克力管为仿体材料,长度为300 mm,其余参数均与仿真材料参数一致。在该长度下,端面反射不会对接收信号产生影响。实验装置如图4所示。由PC机将信号送至信号发生器(Agilent 33220A,CO,USA),再经过功率放大器(AG 1021,T&C power conversion,Inc.,NY,USA)放大后作为发射探头T的激励信号。采用宽带脉冲超声分析仪(5900PR,Olympus Corp.,MA,USA)对由探头R接收到的超声信号完成滤波及预处理。发射探头和接收探头中心频率均为0.3 MHz(Valpey fisher corp.,USA)。实验所用激励信号与仿真激励信号相同。经由示波器(HP54642A,CA,USA)采集数据后,通过GPIB接口送至PC机以供后续分析。实验中采用三维扫描系统(Physical acoustics corp.,NJ,USA)控制两探头的间距,探头与亚克力管接触位置均有耦合剂耦合。
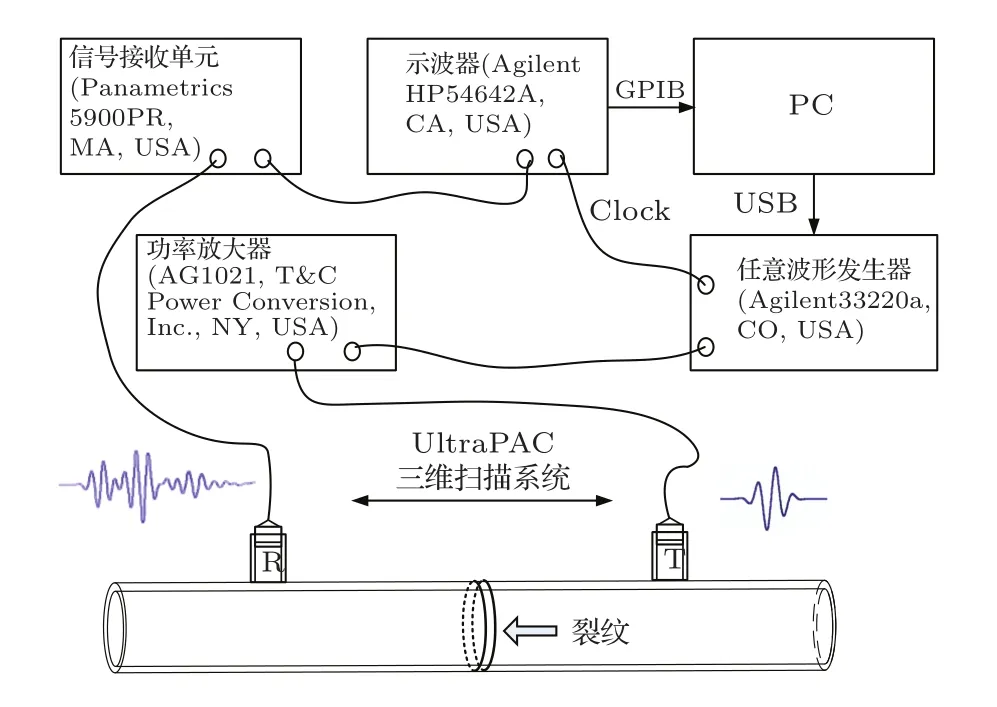
图4 实验装置图Fig.4 Experimental apparatus
3.3信号分析
为了方便模式分离,对接收信号进行希尔伯特变换得到信号包络。希尔伯特变换定义为
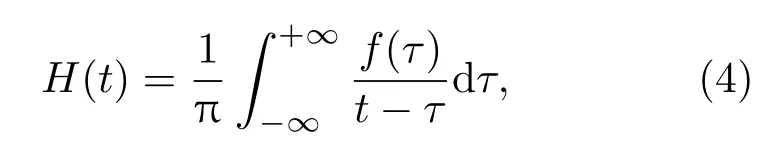
其中H(t)是信号f(t)的希尔伯特变换,公式(4)实质上是信号在频率域作90°相移,得到FA(t):
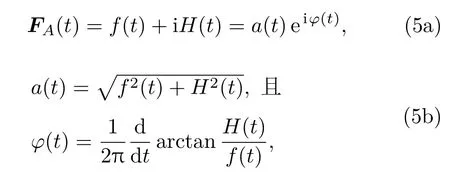
其中a(t)为信号f(t)的上包络。对包络求极大值点,并以极值点为矩形窗的中心,窗宽与激励信号长度相等(20µs),将矩形窗与接收信号相乘即可实现模式分离。在不同裂纹程度下,对接收信号分别计算各模式峰值点与激励信号峰值点的时间差,并已知探头间距,即可得到不同裂纹程度下各模式的群速度,并对计算所得的结果取均值。各模式的能量为采样点幅度的平方和。
4 仿真与实验结果
4.1仿真结果
图5(a)给出了200 kHz四周期的激励下,2.5 mm厚度亚克力管的仿真结果。其中快波包为L(0,2)模式,慢波包为L(0,1)模式,处于两模式之间的波包是转换模式。由图可得随裂纹程度增加(0%—80%),转换模式明显增强。图5(b)所示为群速度结果,实线、虚实线、虚线分别表示L(0,2)模式、转换模式、L(0,1)模式群速度的理论曲线。各点代表3种管壁厚度下仿真获得的导波模式速度。1.8 mm,2.5 mm,3.0 mm厚度管中各个导波模式群速度的误差分别为2.87%、3.57%与3.00%。如图5(c)所示,各点代表在不同裂纹程度下各个厚度管所对应的模式能量占总能量的百分比。图中的直线表示了一阶线性拟合结果,可观察到随裂纹程度的增加,转换模式逐渐增强。厚度1.8 mm,2.5 mm,3.0 mm的转换模式拟合直线斜率分别为1.07,0.93与0.93。

图5 200 kHz激励下,外半径10 mm厚度2.5 mm亚克力管仿真结果Fig.5 Simulation result of acrylic tube with the external radius of 10 mm and thickness of 2.5 mm under 200 kHz motivation
4.2实验结果
图6(a)给出了200 kHz激励下,2.5 mm厚度亚克力管的仿体实验结果。其中快波包为L(0,2)模式,慢波包为L(0,1)模式,处于两模式之间的波包是转换模式。由图可得随裂纹程度增加(0%—80%),转换模式明显增强。图6(b)所示为群速度结果,实线、虚实线、虚线分别表示L(0,2)模式、转换模式、L(0,1)模式群速度的理论曲线。各点代表3种管壁厚度下仿体实验获得的导波模式速度。1.8 mm,2.5 mm,3.0 mm厚度管中各个导波模式群速度的误差分别为10.27%、2.48%与6.79%。如图6(c)所示,各点代表在不同裂纹程度下各个厚度的亚克力管所对应的模式能量比。图中的直线表示了一阶线性拟合结果,可观察到随裂纹程度的增加,转换模式逐渐增强。厚度1.8 mm,2.5 mm,3.0 mm的转换模式的拟合直线斜率分别为0.69,0.48与0.65。
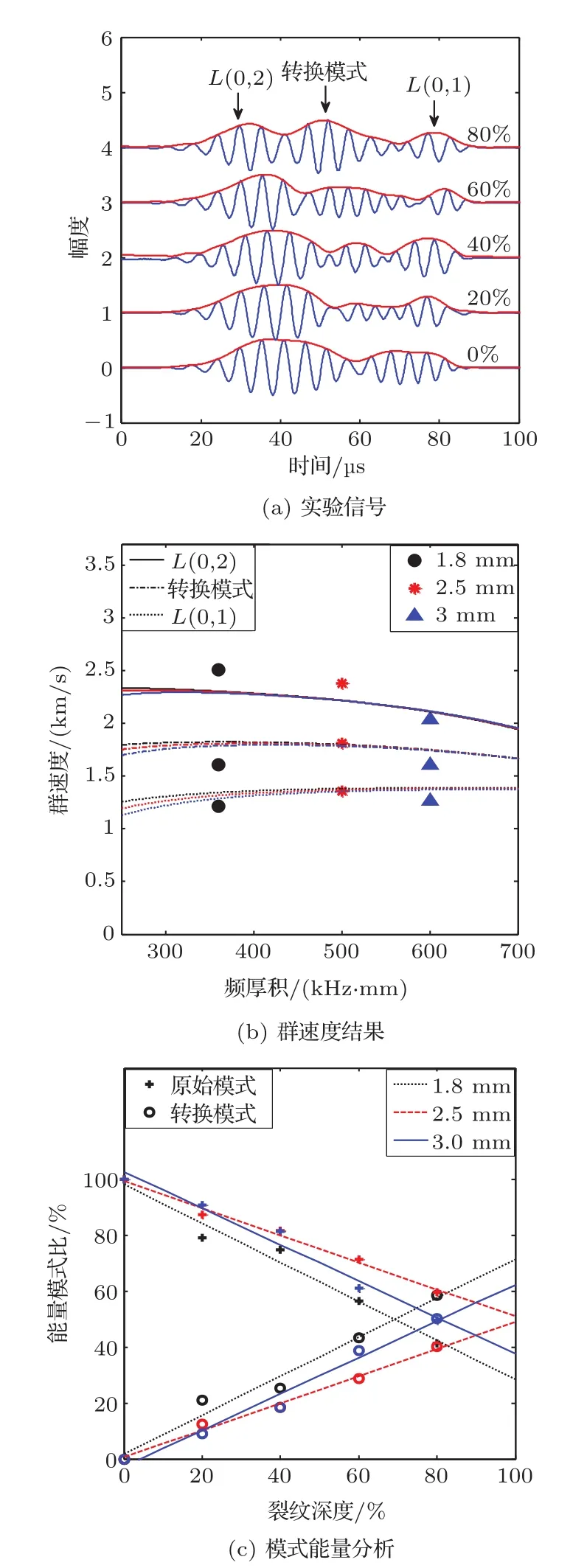
图6 200 kHz激励下,外半径10 mm厚度2.5 mm亚克力管实验结果Fig.6 Experimental result of acrylic tube with the external radius of 10 mm and thickness of 2.5 mm under 200 kHz motivation
5 讨论
长骨皮质骨作为一种复杂的管状波导,可支持多种导波模式的传播。采用宽带激励法所获得的导波信号中往往会包含在时频域相互混叠的多个模式成份,较难实现模式分离与后续定量参数提取。目前已有多种信号分析技术被应用于基于超声导波技术的长骨骨质状况评价,如时频分析法[13,28]、盲信号分离法[29]等。但是,由于骨折长骨中还会发生复杂的模式转换现象,直接采用上述方法仍不能完全解决导波信号模式分离及处理。为减少激励出的导波模式并简化模式分离,本文研究中采用了低频窄带的激励方式[3,19-20,30]。仿真与实验表明,0.2 MHz的低频激励能够保证仅激发出两个最基本的纵向导波模式L(0,1)与L(0,2),为后续的处理工作带来了便利。但由于传播距离较短,且各导波模式波长较长,因而两个转换模式L(0,2)L(0,1)与L(0,1)L(0,2)会混迭为一个波包。同时,参考公式(1)—(2)所给出的速度关系可知,转换模式的表观群速度与裂纹位置有关,即当环切裂纹被置于两探头中间时,L(0,1)模式与L(0,2)模式的表观群速度值基本相等。因而,在有关模式转换能量系数的讨论中,未能对L(0,2)L(0,1)与L(0,1)L(0,2)进行分离。
从仿真和实验结果来看,模式能量比与裂纹深度具有一定的线性关系。因此,将超声导波的模式能量比应用于长骨裂纹深度评估具有较好的可行性。但考虑到临床上的实际情况,应当建立包含软组织与骨髓的三层长骨模型,讨论软组织对超声导波传播与模式转换的影响。本研究中采用了固定长度的时间窗实现原始模式与转换模式的分离,该方法在一定程度上会影响导波模式速度与模式转换能量比的计算,如何更好的实现模式分离的也是值得改进的方向。本文仅在同一位置接收超声导波信号,如能在多个位置得到趋势一致的转换模式关系,则该结论会更加可靠。同时,超声导波在骨折裂纹处的模式转换也可进一步被用于评价长骨皮质骨骨折愈合状况,为超声骨折愈合临床监测提供理论基础与技术支持。
由于实际长骨的复杂性,求解其中的波动方程非常复杂,因此,目前还没有人研究关于长骨形状的不规则性对超声导波传播的影响,因此还需作进一步研究。
6 结论
本文结合超声导波理论,采用三维时域有限差分(3D-FDTD)仿真方法建模分析了管状结构中的导波模式转换规律及其量化评价参数。在此基础上进行亚克力管仿体实验,探讨基于模式转换评价长骨裂纹状况的可行性。
仿真与仿体实验表明,在200 kHz窄带信号的激励下,完好亚克力管中主要存在L(0,2)模式为主要成分的快波波包和L(0,1)模式为主要成分的慢波波包;而在含裂纹亚克力管中除了原有透射导波模式以外,还会产生转换模式波包。且处于原有快波和慢波之间。将各种模式分离之后,模式能量百分比可用于指示模式转换程度,进而评价长骨的骨裂状况。
本文实现了将模式转换能量分析应用于长骨骨折评估可行性的初步研究,为基于超声导波技术的骨折诊断提供理论基础。
[1]王亦璁,孟继懋,郭子恒.骨与关节损伤[M].北京:人民卫生出版社,1999.
[2]LAUGIERP,HAÏATG.Bonequantitativeultrasound[M].New York:Springer,2010.
[3]MOILANEN P.Ultrasonic guided waves in bone[J].IEEE Trans.UFFC,2008,55(6):1277-1286.
[4]PROTOPAPPAS V C,VAVVA M G,FOTIADIS D I,et al.Ultrasonic monitoring of bone fracture healing[J]. IEEE Trans.UFFC,2008,55(6):1243-1255.
[5]张正罡,他得安,王威琪.基于弹性模量检测骨疲劳的超声导波方法研究[J].物理学报,2012,61(13):134304. ZHANG Zhenggang,TA Dean,WANG Weiqi.Study of bone fatigue evaluation with ultrasonic guide waves basedon elastic modulus[J].Acta Phys.Sin.,2012,61(13):134304.
[6]SONG X J,TA D A,WANG W Q.A base-sequencemodulated golay code improves the excitation and measurement of ultrasonic guided waves in long bones[J]. IEEE Trans.UFFC,2012,59(11):2580-2583.
[7]LE L H,GU Y J,LI Y,et al.Probing long bones with ultrasonic body waves[J].Appl.Phys.Lett.,2010,96(11):114102.
[8]TA D A,WANG W Q,WANG Y Y,et al.Measurement of the dispersion and attenuation of cylindrical ultrasonic guided waves in long bone[J].Ultrasound Med. Biol.,2009,35(4):641-652.
[9]TA D A,HUANG K,WANG W Q,et al.Identification and analysis of multimode guided waves in tibia cortical bone[J].Ultrasonics,2006,44:e279-e284.
[10]刘洋,郭霞生,章东,等.基于时间反转的骨裂纹超声成像模拟研究[J].声学学报,2011,36(2):179-184. LIU Yang,GUO Xiasheng,ZHANG Dong,et al.A simulation study of ultrasonic imaging of micro-crack in bone based on time-reversed approach[J].Acta Acustica,2011,36(2):179-184.
[11]许凯亮,他得安,王威琪.骨折长骨中超声导波传播特性的仿真研究[J].声学学报,2009,34(5):423-429. XU Kailiang,TA Dean,WANG Weiqi.Simulation of propagation characteristics of ultrasonic guided waves in fracture long bone[J].Acta Acustica,2009,34(5):423-429.
[12]张慧琳,宋小军,他得安.Barker码激励超声导波在长骨检测中的应用[J].声学学报,2014,39(2):257-263. ZHANG Huilin,SONG Xiaojun,TA Dean.Application of Barker code excited ultrasonic guided waves to long bone detection[J].Acta Acustica,2014,39(2):257-263.
[13]XU K L,TA D A,WANG W Q.Multiridge-based analysis for separating individual modes from multimodal guided wave signals in long bones[J].IEEE Trans.UFFC,2010,57(11):2480-2490.
[14]XU K L,TA D A,SU Z Q,et al.Transmission analysis of ultrasonic Lamb mode conversion in a plate with partialthickness notch[J].Ultrasonics,2014,54(1):395-401.
[15]SU Z Q,YE L.Identification of damage using lamb waves:from fundamentals to applications[M].Berlin:Springer,2009.
[16]SU Z,YE L,LU Y.Guided Lamb waves for identification of damage in composite structures:a review[J].J.Sound Vib.,2006,295(3):753-780.
[17]PROTOPAPPAS V C,FOTIADIS D I,MALIZOS K N. Guided ultrasound wave propagation in intact and healing long bones[J].Ultrasound Med.Biol.,2006,32(5):693-708.
[18]PROTOPAPPAS V C,KOURTIS I C,KOURTIS L C,et al.Three-dimensional finite element modeling of guided ultrasound wave propagation in intact and healing long bones[J].J.Acoust.Soc.Am.,2007,121(6):3907-3921.
[19]XU K L,LIU D,TA D A,et al.Quantification of guided mode propagation in fractured long bones[J].Ultrasonics,2014,54(5):1210-1218.
[20]XU K L,TA D A,HE R X,et al.Axial transmission method for long bone fracture evaluation by ultrasonic guided waves:simulation,phantom and in vitro experiments[J].Ultrasound Med.Biol.,2014,40(4):817-827.
[21]刘丹,许凯亮,李大为,等.超声导波定量评价长骨骨折状况[J].中国科学G:物理学力学天文学,2014,44(7):682-690. LIU Dan,XU Kailiang,LI Dawei,et al.Quantitative evaluation of long bone fractures by ultrasonic guided waves[J].Sci Sin-Phys.Mech.Astron.,2014,44(7):682-690.
[22]他得安,刘镇清.充粘液管材中超声纵向轴对称导波的频散特性分析[J].声学学报,2005,30(3):193-200. TA Dean,LIU Zhenqinq.Analysis of dispersion characteristics of ultrasonic longitudinal axisymmetric guidedwaves in viscous liquid-filled pipes[J].Acta Acustica,2005,30(3):193-200.
[23]ROSE J L.Ultrasonic waves in solid media[M].Cambridge:Cambridge university press,2004.
[24]MOILANEN P,NICHOLSON P,KILAPPA V,et al. Measuring guided waves in long bones:modeling and experiments in free and immersed plates[J].Ultrasound Med.Biol.,2006,32(5):709-719.
[25]CHEN J,SU Z.On ultrasound waves guided by bones with coupled soft tissues:a mechanism study and in vitro calibration[J].Ultrasonics,2014,54(5):1186-1196.
[26]LIU C C,HAN H J,TA D A,et al.Effect of selected signals of interest on ultrasonic backscattering measurement in cancellous bones[J].Sci.China Phys.Mech.& Astron.,2013,56(7):1310-1316.
[27]GSELL D,LEUTENEGGER T,DUAL J.Modeling three-dimensional elastic wave propagation in circular cylindrical structures using a finite-difference approach[J]. J.Acoust.Soc.Am.,2004,116(6):3284-3293.
[28]罗春苟,他得安,李维,等.时频方法分析长骨中的超声导波及皮质骨厚度[J].声学学报,2009,34(5):416-422. LUO Chungou,TA Dean,LI Wei,et al.Analysis of ultrasonic guided waves in long bone and cortical bone thickness using time-frequency methods[J].Acta Acustica,2009,34(5):416-422.
[29]宋小军,他得安,王威琪.基于时频分布的盲信号分离方法研究长骨中的多模式导波信号[J].声学学报,2011,36(3):318-324. SONG Xiaojun,TA Dean,WANG Weiqi.Study on the multiple guided waves in long bones using spatial timefrequency based blind source separation method[J].Acta Acustica,2011,36(3):318-324.
[30]KILAPPA V,XU K,MOILANEN P,et al.Assessment of the fundamental flexural guided wave in cortical bone by an ultrasonic axial-transmission array transducer[J]. Ultrasound Med.&Biol.,2013,39(7):1223-1232.
Long bone fracture evaluation using ultrasonic guided waves:a phantom study
HU ShixiaoXU KailiangTA Dean
(Department of Electronic Engineering,Fudan University,Shanghai 200433,China)
Using ultrasonic guided waves to assess long bone fracture status has drawn significant research interests.The study aimed to investigate the feasibility of ultrasonic guided-mode conversion theory for long cortical bone fracture evaluation.In this article,the principle of guided waves mode conversion in the fractured long bone was analyzed using three-dimension finite-difference time-domain(3D-FDTD),and quantitative parameters were proposed to evaluate the fracture status.The mode conversion theory was applied to analyze different fractures in phantom experiment.Both numerical simulation and phantom experiment indicated that the energy parameter of ultrasonic guided mode conversion correlated strongly with fracture depth,which may offer great potentials for the long bone fracture evaluation.
Long bone fracture,Ultrasonic guided waves,Mode conversion,3D-FDTD
R445.1,O426.9
A
1000-310X(2015)02-0095-07
10.11684/j.issn.1000-310X.2015.02.001
2014-07-15收稿;2014-09-08定稿
∗国家自然科学基金项目(11174060,11304043,11327405),教育部博士点基金(20110071130004,20130071110020),上海市科技支撑计划(13441901900)及中国博士后基金项目(2012M520826)
胡时晓(1991-),男,浙江海宁人,硕士研究生,研究方向:生物医学超声。
E-mail:tda@fudan.edu.cn
