小直径开缝衬套双轴柔性滚弯成形的三维有限元分析

龚靖平　黎向锋　左敦稳　康晓军　邱佳斌

南京航空航天大学，南京，210016

小直径开缝衬套双轴柔性滚弯成形的三维有限元分析

龚靖平黎向锋左敦稳康晓军邱佳斌

南京航空航天大学，南京，210016

基于双轴柔性滚弯技术原理,建立了采用0Cr15Ni7Mo2Al材料制备小直径开缝衬套过程的三维有限元模型,以指导实际小直径开缝衬套的制备。利用该模型分析了衬套应力应变分布、刚性轴受力变形情况、衬套成形曲率半径与刚性轴直径的关系及衬套成形曲率半径与带材尺寸的关系,并用滚弯试验验证了该模型的准确性。结果说明:带材滚弯变形随着进给量的增加而更均匀；刚性轴受力随其直径的减小而减小,刚性轴变形程度随其直径的减小而增大；衬套成形曲率半径随着刚性轴直径的增大而增大；衬套成形曲率半径随着带材宽度和厚度的增大而增大。

有限元;小直径开缝衬套;双轴柔性滚弯;0Cr15Ni7Mo2Al;冷挤压

0　引言

孔的开缝衬套冷挤压强化技术具有干涉量大、操作性强、挤压质量高的特点,能够显著延长多种材料结构件的使用寿命，已广泛应用于飞机紧固孔的强化[1-3]。开缝衬套是该强化技术中的关键组成部分,制造要求高、难度大。目前，世界上最成熟的开缝衬套制备供应商是美国疲劳技术公司和西海岸产业公司。南京航空航天大学提出双轴柔性滚弯技术,并成功运用在开缝衬套的制造中[4]。上世纪90年代,南京航空航天大学利用双轴柔性滚弯技术成功制备出开缝衬套后,相继开展了一系列理论研究[5-8]。随着有限元理论的不断完善,有限元仿真技术也应用于柔性滚弯的研究中。闫静等[9]建立了双轴柔性滚弯二维有限元模型,模拟了滚弯成形和回弹过程。鲁世红等[10]提出了折算弹性模量的概念,用于定义双轴柔性滚弯中聚氨酯橡胶的弹性模量,并将其应用于滚弯过程的仿真研究。已有的有限元模型均是将滚弯过程简化为二维平面模型进行分析,而实际的双轴柔性滚弯制备开缝衬套是一个三维动态过程,二维模型必然忽略了某些因素的影响，但衬套长度对衬套成形尺寸的影响不容忽略。

目前，国内生产的开缝衬套直径在27 mm以上,适用于大直径紧固孔,而飞机蒙皮等多处有较多小直径孔(尺寸范围在6 ～18 mm)。可见国内生产的开缝衬套规格远不能满足国内飞机的生产与维修的要求[11]。制备小直径开缝衬套对设备提出了更高要求,且需要解决刚性轴刚度不足、带材加工硬化及成形衬套取出困难等问题,故亟待开展小直径开缝衬套制备及仿真研究。本文采用有限元分析软件ABAQUS,基于双轴柔性滚弯技术原理,对采用0Cr15Ni7Mo2Al带材制备小直径(20 mm以下)开缝衬套的过程进行了三维有限元模拟,并通过试验进行了模型验证。利用该模型分析了衬套应力应变分布、刚性轴受力变形情况、刚性轴直径和带材尺寸对衬套成形曲率半径的影响。

1　双轴柔性滚弯技术原理

双轴柔性滚弯技术原理如图1所示,弹性轮为主动轮,刚性轴为从动轴,由弹性轮转动带动刚性轴转动。在压力p的作用下,刚性轴产生进给量f，弹性轮发生弹性变形而产生相应的分布载荷。该分布载荷使带材逐步屈服，并使带材在离开两轴后仍能保持曲率半径r。送料则通过带材与刚性轴和弹性轮间的摩擦完成。双轴柔性滚弯制备出的开缝衬套如图2所示，其主要外形特征有衬套成形曲率半径、衬套厚度、衬套长度及搭边。

图1　双轴柔性滚弯原理图

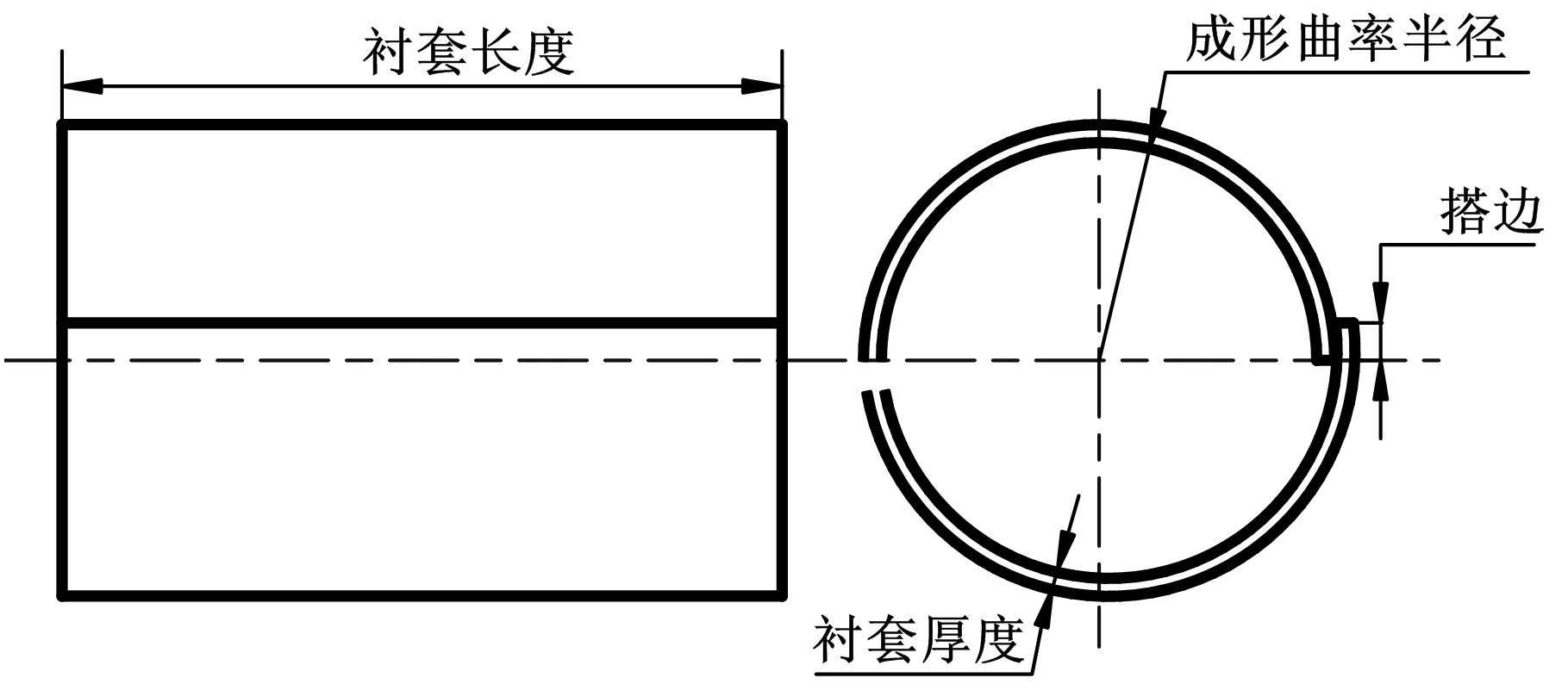
图2　开缝衬套外形特征

2　有限元模型

利用双轴柔性滚弯技术制备开缝衬套属于板材弹塑性变形问题，涉及材料非线性、几何非线性及边界非线性，进行理论研究较为困难。有限元模拟技术能够直观高效地分析金属成形过程，并克服了实验成本高、周期长的缺点。建立准确的三维有限元模型，关键在于获取弹性轮和带材材料的物性参数，合理划分网格，定义正确的接触和边界条件。

2.1几何模型

刚性轴在滚弯过程中不发生变形,定义为刚体。为制备直径20 mm以下的开缝衬套,应采用直径小于14 mm的刚性轴[4]。本文设置的刚性轴直径为11 mm，长度为40 mm。在刚性轴轴线中点设置一参考点,以便控制刚性轴的进给。弹性轮采用过盈配合固定在芯轴上,芯轴不影响滚弯过程,故不建立芯轴模型,将弹性轮简化为圆环柱体。根据试验设备设置弹性轮内径为56 mm,外径为160 mm，厚度为30 mm。带材为一矩形薄板，其尺寸为58.2 mm×25.4 mm×0.45 mm。

2.2材料模型

刚性轴为刚体,不需定义材料模型。弹性轮材料为聚氨酯橡胶,属于大变形、非线性、几乎不可压缩的超弹性材料。对于超弹性材料,ABAQUS采用应变势能来表达应力应变关系,常用的应变势能模型有Mooney-Rivlin模型、Yeoh模型、neo-Hookean模型及Wgden模型等,其中,Mooney-Rivlin模型形式简单、系数获取方便,应用广泛,其应变势能形式为

W=C10(l1-3)+C01(l2-3)+(J-1)2/D1

(1)

式中,l1、l2分别为第一、第二Green应变不变量;J为弹性体积比;系数C10、C01可由单向拉伸应力应变关系得出;D1与初始体积模量有关的材料参数。

本文的弹性轮材料模型为Mooney-Rivlin模型,只需输入系数C10、C01和D1。对于硬度为90A的弹性轮,C10=3.58，C01=0.48,D1=0.0125,弹性轮密度为1.25 g/cm3,弹性模量为25 MPa[12-13]。

材料0Cr15Ni7Mo2Al属于半奥氏体沉淀硬化不锈钢，易于冷加工成形，被广泛应用在航空薄壁结构件,各种弹簧、管道和阀膜等部件[14]。为获取该材料物性参数,以表征滚弯仿真过程中带材的弹塑性变形,在微机控制电子万能试验机RG2000-04上进行拉伸试验，获得材料应力-应变曲线,如图3所示。带材材料密度为7.685 g/cm3,弹性模量为185 GPa,泊松比为0.3。

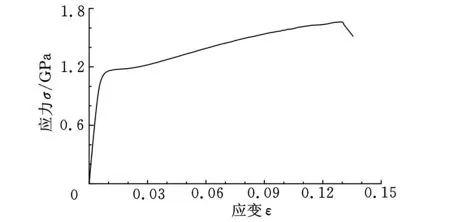
图3　0Cr15Ni7Mo2Al材料的应力-应变曲线

2.3网格划分

滚弯过程属于复杂的三维接触问题，存在较大的网格变形，三维八节点六面体缩减积分单元C3D8R能以合理的计算成本得到精确结果，故本模型均采用此单元类型[15]。为保证较高的计算精度，并缩短计算时间，对弹性轮进行非均匀网格划分：接触部分的网格最为细密，过渡部分的网格密度次之，小变形部分的网格较疏松。带材变形为模拟分析的重点，网格划分均匀且细密，带材厚度方向划分为三层。刚性轴是刚体，不需划分网格。整体模型的网格划分如图4所示。

图4　整体模型的网格划分

2.4边界条件及分析步定义

有限元模拟中，使变形体旋转的方法还未完善[16]，故本文将滚弯过程进行等效转化,即把弹性轮转动带动刚性轴的转动转化为弹性轮固定、刚性轴转动。将滚弯模拟分为三步分析：

(1)根据实际滚弯设备中弹性轮与芯轴的过盈配合量，在弹性轮内圈施加2 mm的径向位移，来模拟过盈配合给弹性轮带来的挤压。

(2)给予刚性轴参考点沿径向预设的位移，模拟刚性轴进给。

(3)给予刚性轴参考点转角位移，使刚性轴绕轴线转动，模拟滚弯成形过程。滚弯车床转速为10 r/min,则安装在车床上的弹性轮转速也为10 r/min,由转速与轴径的关系得刚性轴转速为15.27 rad/s。带材长度为58.2 mm,要使带材随着刚性轴转动而全部送入，则刚性轴约转动1.68圈(58.2/(11π)=1.68),即刚性轴至少转动10.56 rad，这需要0.69 s(10.56/15.27=0.69)。考虑带材不可能完全贴合刚性轴表面滚弯，且存在相对滑动，最终设置该分析步时间为0.8 s,刚性轴转角为12 rad。

由于滚弯结束后，衬套不可避免地发生回弹，故再定义一个分析步模拟回弹过程。在该分析步中，约束已滚弯成形的带材一端所有方向的自由度，让带材另一端释放应力，直至带材外形稳定。

2.5接触定义

滚弯过程中，带材、刚性轴和弹性轮两两接触，且带材与弹性轮、带材与刚性轴的接触均有滚动摩擦力，存在小的相对滑动。故接触滑动方式采用有限滑移，即两个接触面之间可以有任意的相对滑动。为保证顺利送料，带材与刚性轴间的摩擦力应大于带材与弹性轮间的摩擦力，即前者的摩擦因数应大于后者的摩擦因数，对各接触对进行设置如表1所示。

表1　接触设置

3　有限元模型验证

(a)刚性轴进给

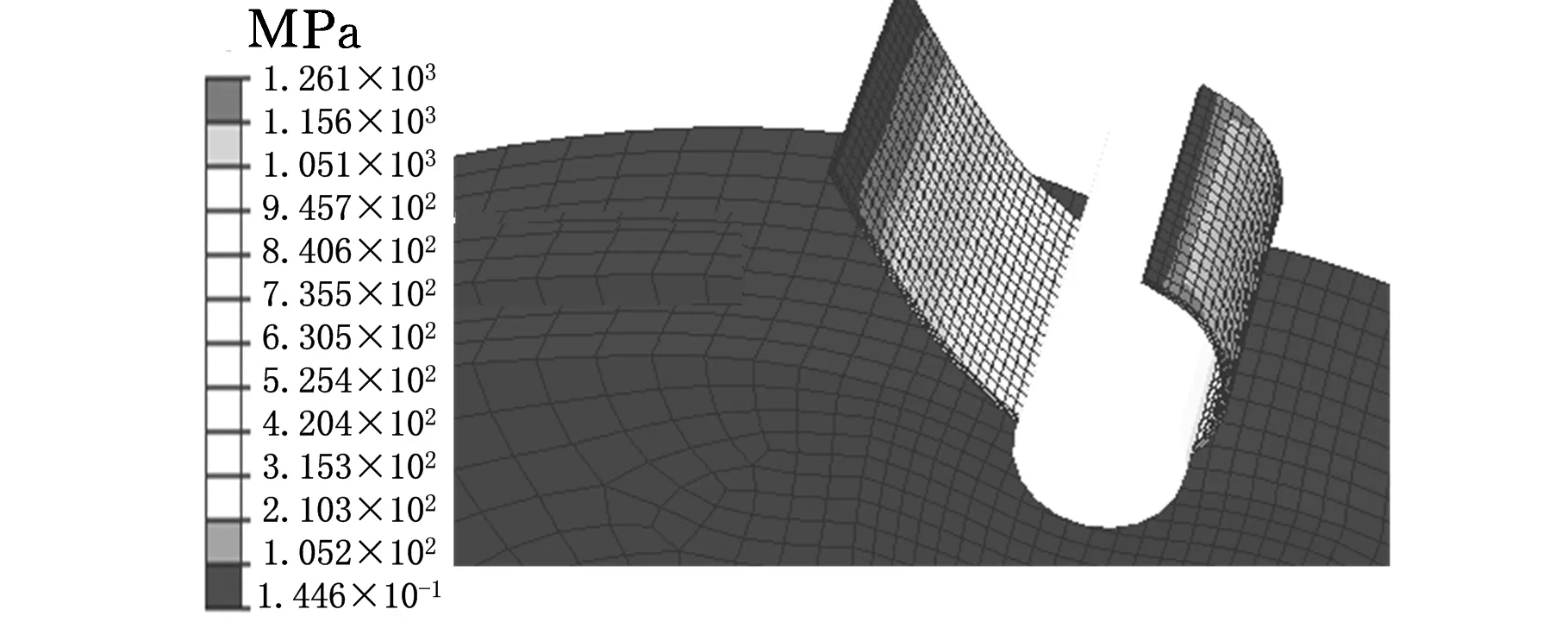
(b)带材滚弯变形

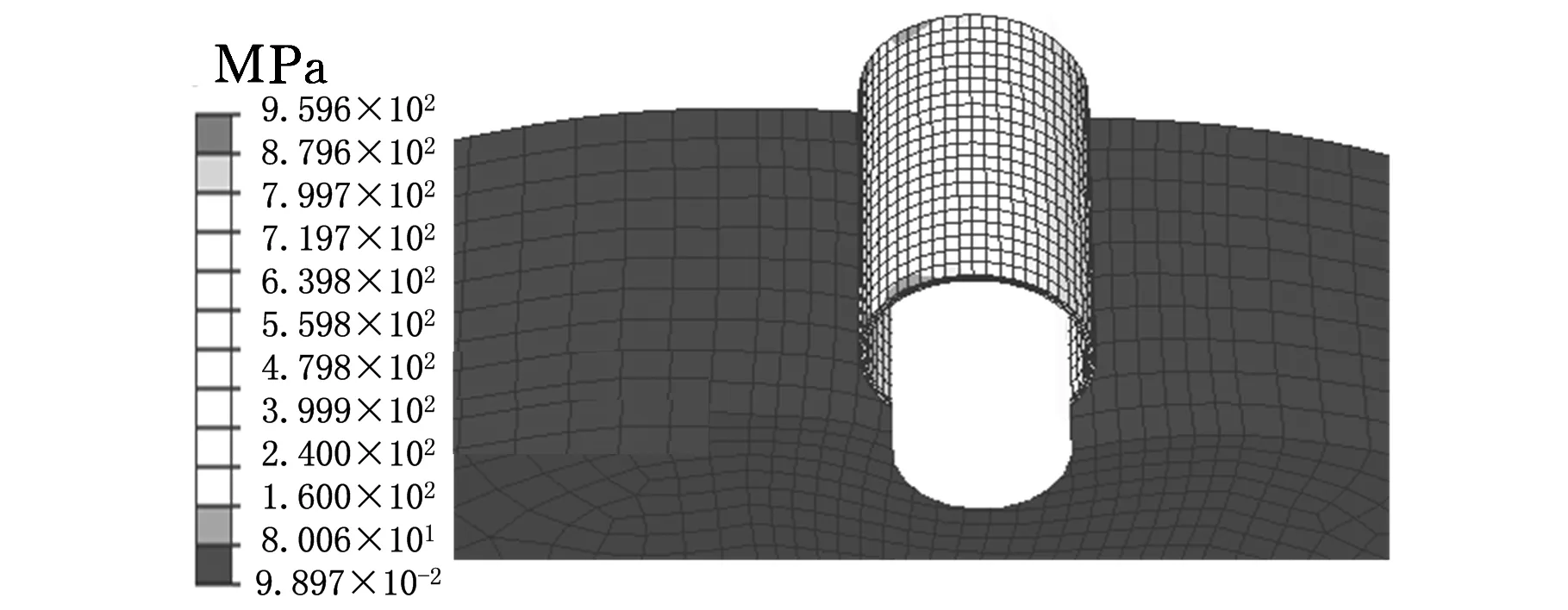
(c)带材滚弯成形

(d)回弹图5　双轴柔性滚弯模拟过程

双轴柔性滚弯制备开缝衬套的模拟过程如图5所示,可分为4个阶段:①刚性轴沿径向进给，压入弹性轮；②刚性轴转动，由摩擦力实现送料，带材开始滚弯变形；③带材在弹性轮挤压力下逐渐滚弯成形；④成形件发生回弹,释放应力。

3.2双轴柔性滚弯试验

为验证该有限元模型，进行双轴柔性滚弯试验。试验用刚性轴、弹性轮和带材规格均与有限元模型参数相同,试验在CA6140车床上进行。如图6所示，弹性轮装配在芯轴上，随芯轴安装在三爪卡盘上，并用顶尖定位。刚性轴由专用夹具装夹，夹具安装在刀架上。试验时,机床主轴的最低转速为10 r/min，在刚性轴进给量为4 mm、5 mm和6 mm条件下制备衬套,试验制备衬套与仿真衬套如图7、图8所示。由于ABAQUS软件后处理操作无法直接读取衬套成形曲率半径，故提取仿真结果中衬套端面节点坐标值，将其导入MATLAB程序，采用最小二乘法进行曲线拟合，得到衬套成形曲率半径。试验制备的衬套用游标卡尺测量其成形曲率半径，将其与仿真衬套成形曲率半径进行比较,如表2所示。

图6　双轴柔性滚弯试验

表2　衬套成形曲率半径的试验值与仿真值 mm

由图7、图8可见，不同进给量下成形衬套的试验制品与仿真结果外形相似。由表2可见，有限元仿真值与试验值的变化趋势相同,即成形曲率半径随着进给量的增大而减小，在进给量为5 mm之后,成形曲率半径基本保持不变,此时的衬套成形曲率半径可称为成形极限尺寸[4]。仿真值均小于试验值,误差在15%～20%之间。误差产生的主要原因是有限元模型均为理想化情况，而实际滚弯会存在弹性轮聚氨酯材料老化、带材材料性能不一致等问题,故此误差在可接受范围内,该有限元模型基本准确。

(a)f=4 mm(b)f=5 mm(c)f=6 mm图7　不同进给量的试验制备衬套

(a)f=4 mm(b)f=5 mm(c)f=6 mm图8　不同进给量的仿真衬套

4　有限元分析

4.1衬套应力应变分布

冬至节 冬至是中国农历中一个非常重要的节气，也是达斡尔民族的重要节日。时间在每年的农历12月21至23日之间，这一天是北半球全年白天最短、夜间最长的一天。冬至是家族团聚的一天，这一天，不论贫富，饺子是必不可少的美食。

为研究不同进给量下带材的变形情况及成形质量，模拟分析进给量为4 mm、5 mm和6 mm时带材的等效应力分布及塑性应变分布,如图9、图10所示。

(b)f=5 mm

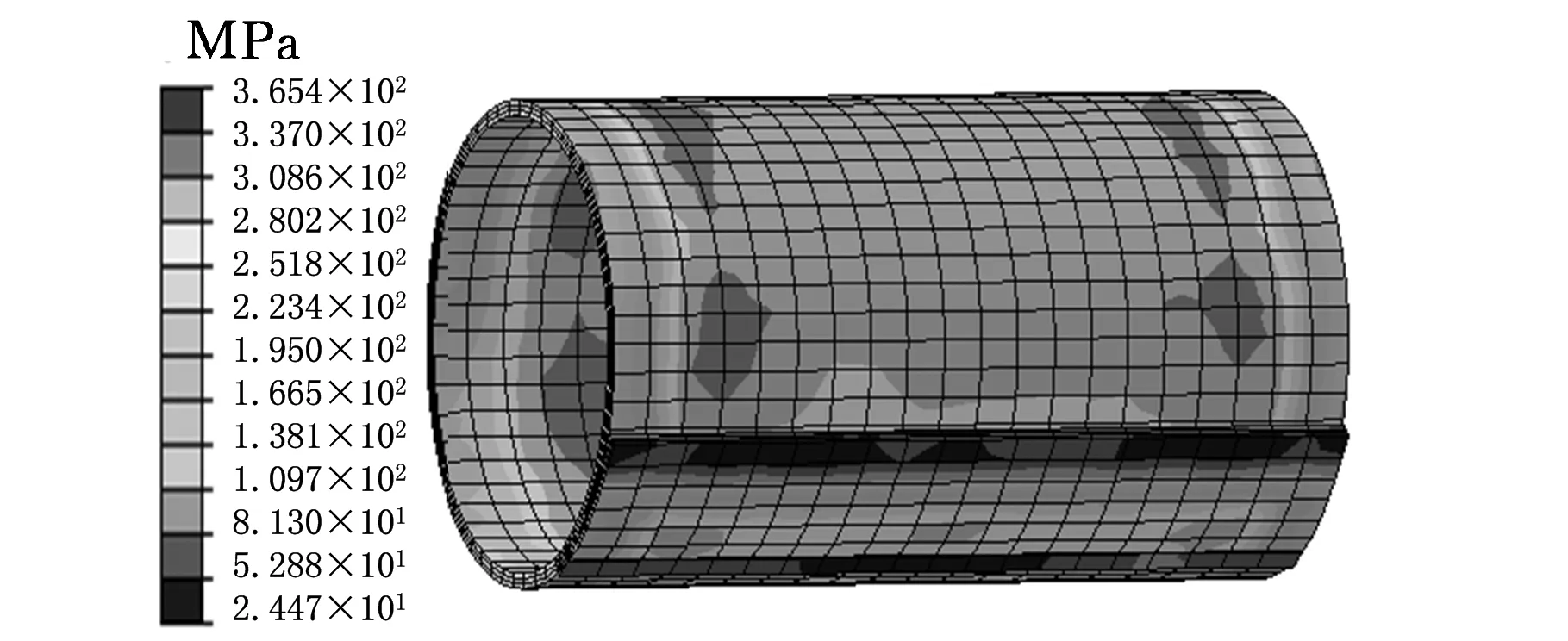
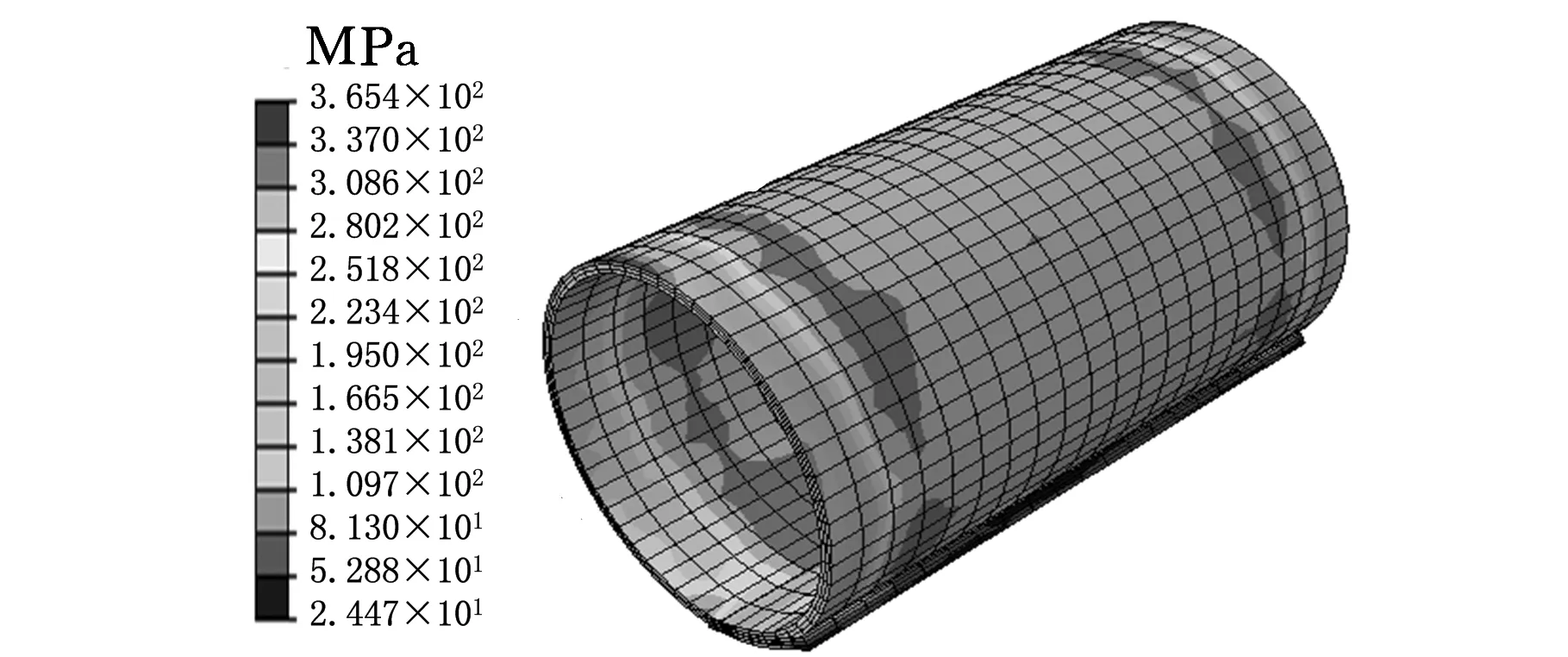
(c)f=6 mm图9　衬套等效应力分布云图

(a)f=4 mm

(b)f=5 mm

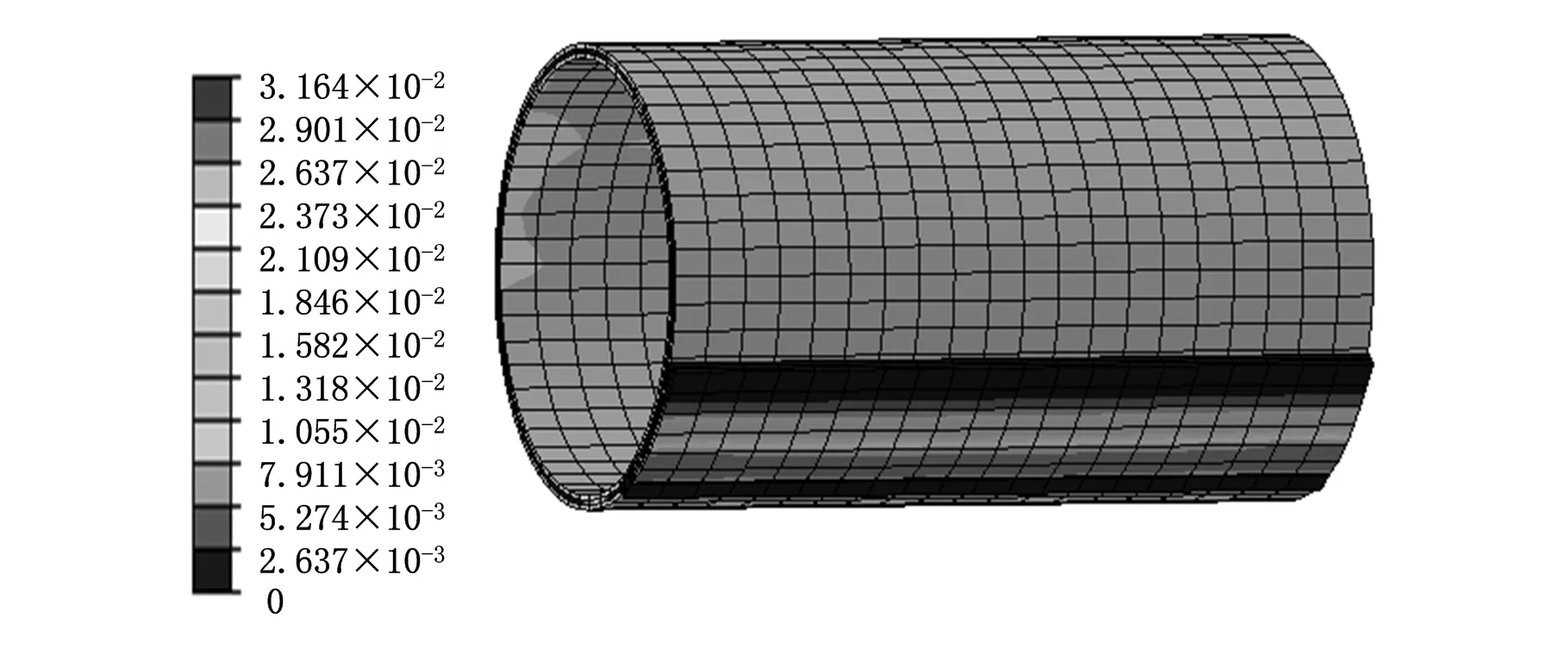
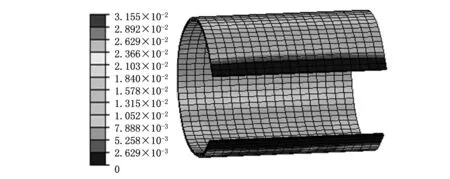
(c)f=6 mm图10　衬套塑性应变分布云图

从图9可见，等效应力分布不均匀,在衬套长度方向,应力主要分布在衬套中部,衬套中部应力为250～380 MPa;衬套搭边处的应力最小,仅为6～25 MPa。塑性应变分布云图颜色分布较一致,且随着进给量的增加,颜色分布更一致,即塑性应变分布更均匀,说明增加进给量可使带材滚弯更充分,变形更均匀。衬套搭边边缘的塑性应变在0.005以下,说明此处带材滚弯变形不足,此种现象称为直边,是衬套成形缺陷之一。在ABAQUS后处理模块中,用距离查询工具测量进给量为4 mm、5 mm和6 mm情况下的直边长度(分别为2.91 mm、1.61 mm和1.41 mm)。可见直边长度随着进给量的增加而减小,说明增加进给量可减小直边长度。

4.2刚性轴受力变形分析

刚性轴受力变形情况直接影响着衬套成形质量,尤其对于小直径开缝衬套的制备,刚性轴刚度问题突出。设置刚性轴直径为8 mm、12 mm、16 mm和20 mm,在进给量为5 mm的条件下进行模拟分析,得到的刚性轴受力如图11所示。不同直径刚性轴的受力曲线相似，刚性轴从0.1 s开始进给,挤压带材及弹性轮产生反作用力。随着刚性轴不断进给，力呈上升趋势直至进给结束(0.4 s)。0.4～1.22 s为带材滚弯变形过程,此时的力在一定范围内波动。受力峰值出现在刚性轴结束进给时,此时的受力最高可达5000 N。由图11可见刚性轴受力随着刚性轴直径的减小而,减小,这是由于刚性轴直径减小使其受力面积减小,从而使刚性轴所受合力减小。

为进一步分析刚性轴的受力变形情况，对其进行刚度分析，将刚性轴受力简化为简支梁受力，有小挠度微分方程：

(2)

式中,ω为轴线长度方向上任一点x处的挠度;M为x处所受弯矩;E为刚性轴材料Q235的弹性模量,E=210 GPa;I为惯性矩,I=πd4/32;d为刚性轴直径。

易知刚性轴的最大挠度在刚性轴中部,刚性轴的最大转角在刚性轴两端。对式(2)进行一次积分并代入仿真受力值，求出最大挠度随时间变化曲线，如图12所示；再进行二次积分，求出最大转角随时间变化曲线，如图13所示。可见刚性轴的最大挠度和最大转角均随着刚性轴直径的减小而增大,当刚性轴直径为8 mm时,最大挠度和最大转角的增大趋势更明显。说明刚性轴直径越小,滚弯时刚性轴弯曲变形程度越大。刚性轴弯曲变形过度易造成衬套腰形缺陷,影响衬套尺寸精度。由式(2)可知,要保证刚性轴刚度应注意选择刚性轴材料和直径,且不宜采用过大的进给量,以免刚性轴受力过大。

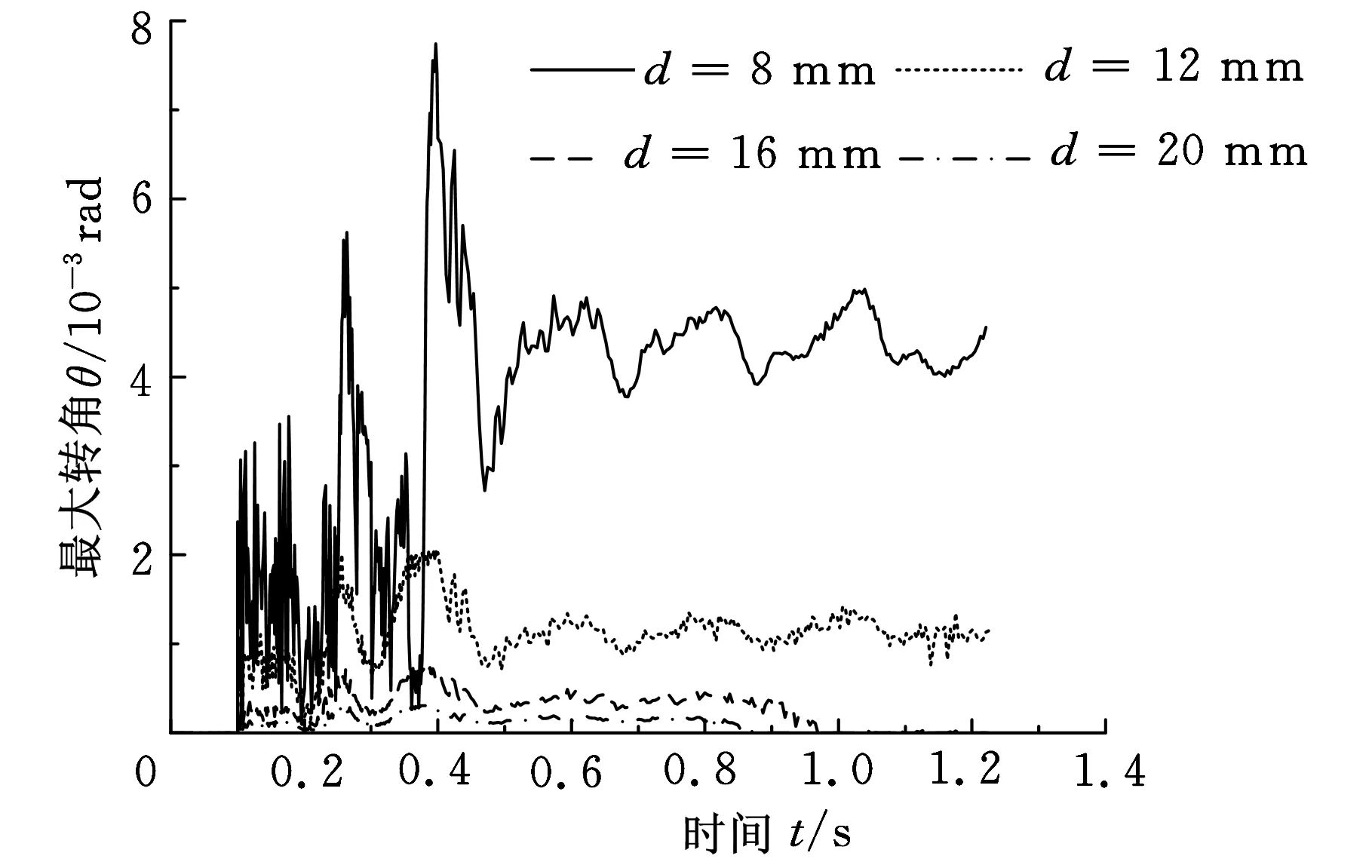
图13　不同直径刚性轴的最大转角变化曲线

4.3成形曲率半径与刚性轴直径关系

刚性轴直径决定了可制备的衬套成形曲率半径范围,制备小直径开缝衬套,需对刚性轴直径作出合理选择。对上述不同直径刚性轴,在进给量为3 mm、4 mm、5 mm和6 mm的情况下进行模拟分析,得到各进给量下衬套成形曲率半径与刚性轴直径的关系曲线,如图14所示。

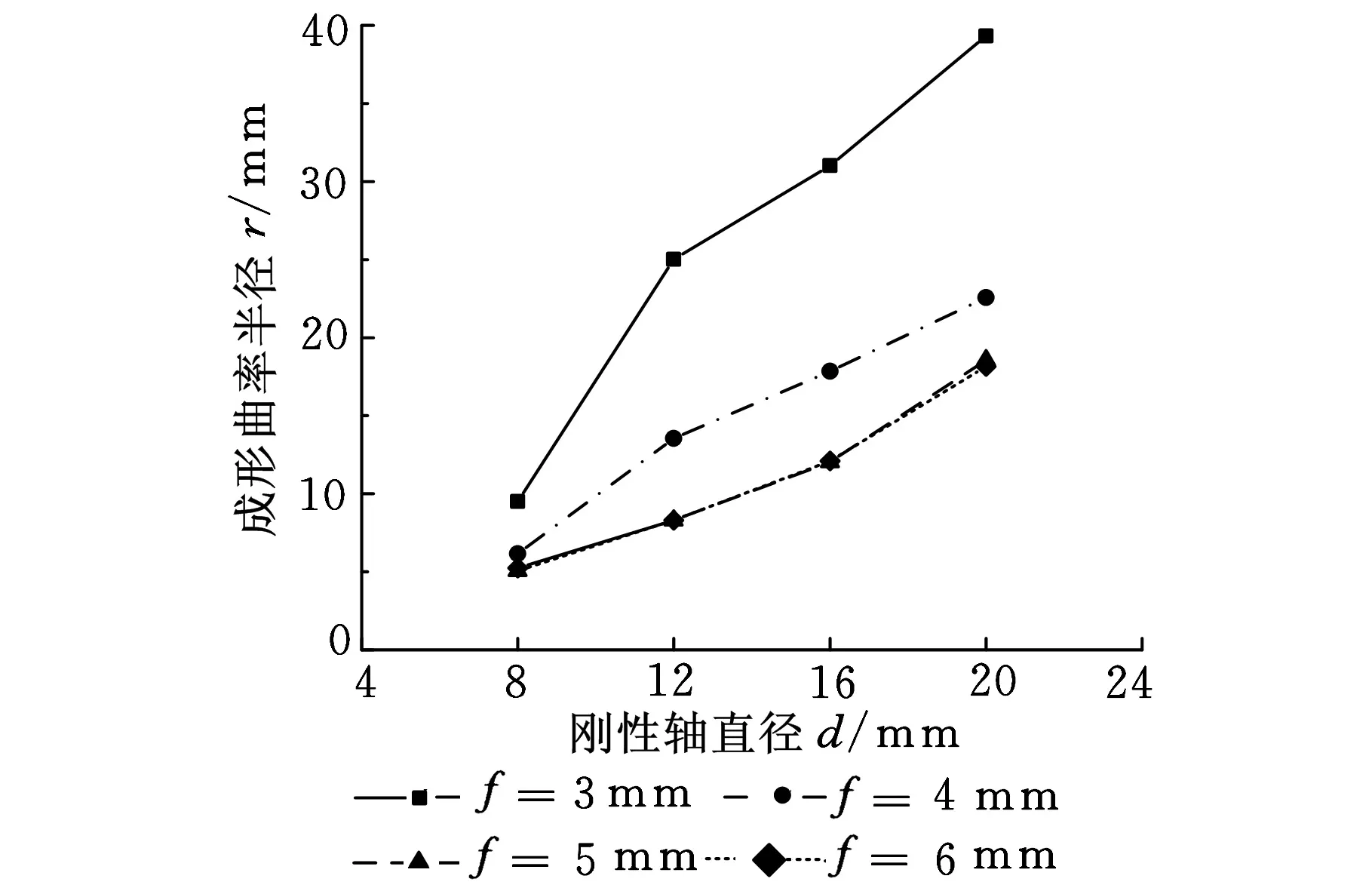
图14　成形曲率半径与刚性轴直径之间的关系

由图14可见,随着刚性轴直径的增大,衬套成形曲率半径增大。进给量5 mm和6 mm的曲线基本重合,说明衬套成形曲率半径不再随着进给量的增加而明显减小,此时的衬套已成形至极限尺寸,也说明了对于不同直径的刚性轴,进给量达5 mm时衬套可成形至极限尺寸。采用Origin数据处理软件对进给量为5 mm的曲线进行拟合,得到成形极限尺寸rw(mm)与刚性轴直径d(mm)间的关系：

rw=0.05d2-0.28d+4.38

(3)

可根据式(3)选择刚性轴直径。

4.4成形曲率半径与带材尺寸关系

已有的有限元研究由于二维模型的局限性，并未讨论带材宽度(衬套长度)对衬套成形曲率半径的影响,故本文利用该三维有限元模型对此进行分析。设置带材宽度分别为10.4 mm、15.4 mm、20.4 mm和25.4 mm,在进给量分别为3 mm、4 mm和5 mm的条件下进行模拟分析,得到成形曲率半径与带材宽度的关系曲线,如图15所示。

图15　成形曲率半径与带材宽度之间的关系

由图15可见,随着带材宽度的增大,成形曲率半径增大。这是因为带材宽度的增加使带材成形所需弯矩增大,在进给量较小时,弹性轮无法提供足够的分布力,故成形曲率半径较大。进给量为5 mm时,不同宽度带材的成形曲率半径基本无变化,说明带材宽度对成形极限尺寸基本无影响。对于宽度小于15.4 mm的带材，当进给量为4 mm时,即可使衬套成形接近极限尺寸,从而可推断对于宽度较小(15.4 mm以下)的带材,使衬套成形至极限尺寸所需的进给量减小。故实际制备衬套时可通过减小带材宽度来减小进给量,以减小刚性轴负载。

带材的宽度与长度均根据被挤压件进行选择，而带材厚度的选择空间较大,故设置带材厚度分别为0.30 mm、0.35 mm、0.40 mm、0.45 mm、0.50 mm和0.55 mm,在进给量为3 mm、4 mm和5 mm条件下进行仿真分析,得到成形曲率半径与带材厚度的关系曲线,如图16所示。由图16可见，随着带材厚度的增大，成形曲率半径增大。进给量为5mm时，不同厚度带材成形曲率半径变化较小，说明带材厚度对成形极限尺寸影响较小。对于厚度小于0.35 mm的带材，当进给量为3 mm时，即可使衬套成形至极限尺寸。这是由于带材厚度的减小，使成形所需弯矩减小，较小的进给量即可提供足够的弯矩使其成形至极限尺寸。综上所述，对于小直径开缝衬套的制备，可选用宽度和厚度较小的带材进行生产，减小进给量以缓解刚性轴直径过小带来的刚度问题。

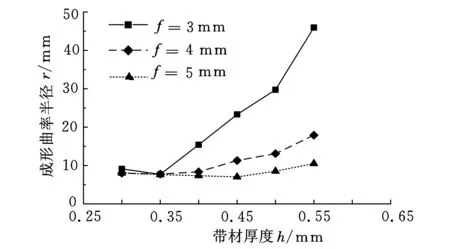
图 16　成形曲率半径与带材厚度之间的关系

5　结论

(1)通过拉伸试验获得了0Cr15Ni7Mo2Al材料的应力应变曲线,并将其应用于有限元模型中的带材材料模型。

(2)建立了双轴柔性滚弯制备开缝衬套过程的三维有限元模型,模拟得出的衬套制备动态过程可分为4个阶段：刚性轴进给、带材滚弯变形、滚弯结束及回弹。滚弯试验验证了该有限元模型的准确性。

(3)利用该模型分析了衬套的应力应变分布：应力主要分布在衬套中部，衬套搭边处的应力较小。带材滚弯变形随着进给量的增加而更均匀，衬套直边长度随着进给量的增加而减小。

(4)对刚性轴受力变形进行了分析，说明刚性轴受力随着刚性轴直径的减小而减小，刚性轴变形程度随着刚性轴直径的减小而增大。

(5)对成形曲率半径与刚性轴直径、成形曲率半径与带材尺寸的关系进行了分析，说明成形曲率半径随着刚性轴直径的增大而增大,对于不同直径的刚性轴，进给量达5 mm时即可使衬套成形至极限尺寸。成形曲率半径随着带材宽度和带材厚度的增大而增大，对于宽度和厚度较小的带材，进给量较小时即可使其成形至极限尺寸。

[1]杨洪源,刘文珽.孔挤压强化疲劳增寿效益的试验研究[J].机械强度,2010,32(3):446-450.

Yang Hongyuan,Liu Wenting.Test Research on Fatigue Life Enhancing Effect of Cold-expanding Hole[J].Journal of Mechanical Strength,2010,32(3):446-450.

[2]Zhang X,Wang Z.Fatigue Life Improvement in Fatigue-aged Fastener Holes Using the Cold Expansion Technique[J].International Journal of Fatigue,2003,25(9/11):1249-1257.

[3]丁传富,赵振业,宋德玉.孔挤压强化对两种超高强度钢疲劳裂纹起始与扩展寿命的影响[J].航空学报,1994,15(8):960-967.

Ding Chuanfu,Zhao Zhenye,Song Deyu.Effect of Cold Worked Holes on the Imitation Life and Propagation Life of Fatigue Cracks in Two Ultra-high Strength Steels[J].Acta Aeronautica et Astronautica Sinica,1994,15(8):960-967.

[4]左敦稳,王珉,刘奎,等.双轴柔性滚弯技术的实验研究[J].南京航空航天大学学报,1998,30(5):6-11.Zuo Dunwen,Wang Min,Liu Kui,et al.Experimental Study on Two-axle Bending Technique[J]. Journal of Nanjing University of Aeronautics & Astronautics，1998，30(5)：6-11.

[5]孙卫祥,左敦稳,曹振中.双轴柔性滚弯数控系统的研究与开发[J].机械制造与自动化,2002(5):26-28.Sun Weixiang,Zuo Dunwen,Cao Zhenzhong.The Research and Development of NC System of Two-axile Flexible Bending[J].Machine Building & Automation,2002(5):26-28.

[6]闫静,左敦稳,王珉.双轴柔性滚弯过程中工件回弹的理论分析[J].兵工学报,2003,24(3):381-384.

Yan Jing,Zuo Dunwen,Wang Min.A Theoretical Analysis on the Springback of Workpiece during Two Axles Bending[J].Acta Armamentar Ⅱ,2003,24(3):381-384.

[7]闫静,王珉,左敦稳.异形截面管双轴柔性滚弯技术理论分析与试验研究[J].机械工程学报,2004,40(11):169-173.

Yan Jing,Wang Min,Zuo Dunwen.Theoretical Analysis and Experimental Study on Two-axle Bending with Elastic Roller for Forming Non-circular Cross-section Parts[J].Chinese Journal of Mechanical Engineering,2004,40(11):169-173.

[8]闫静，左敦稳,王珉.塑性精确理论在双轴柔性滚弯技术中的应用[J].中国机械工程,2005,16(12):1124-1127.

Yan Jing,Zuo Dunwen,Wang Min.Application of the Plastic Precision Theory in Two-axle Bending with Elastic Rollers[J].China Mechanical Engineering,2005,16(12):1124-1127.

[9]闫静,左敦稳,王珉.双轴柔性滚弯技术的有限元分析[J].机械科学与技术,2003,22(2):203-205.

Yan Jing,Zuo Dunwen,Wang Min.FEM Analysis of Two-axle Bending Technique[J].Mechanical Science and Technology,2003,22(2):203-205.

[10]鲁世红,金霞.基于CAE仿真的两轴柔性滚弯过程的应变分析[J].南京航空航天大学学报,2009,41(6):800-804.

Lu Shihong,Jin Xia.Strain Analysis of Two-axle Roll Bending with Elastic Medium Based on CAE Simulation[J].Journal of Nanjing University of Aeronautics & Astronautics,2009,41(6):800-804.

[11]王珉.抗疲劳制造原理与技术[M].南京:江苏科学技术出版社,1999.

[12]何祝斌,林艳丽,孙红岩.型材单辊柔性垫弯曲曲率半径变化规律研究[J].材料科学与工艺,2012,20(5):1-5.

He Zhubin,Lin Yanli,Sun Hongyan. On Curvature Radius of Profiles Bent with Single Roller and

Hyper-elastic Pad[J].Materials Science and Technology,2012,20(5):1-5.

[13]孙家军.U型材单轴柔性滚弯成形技术研究及其有限元分析[D].南京:南京航空航天大学,2008.

[14]陈国辉,张小聪,罗承萍,等.沉淀硬化不锈钢PH15-7Mo的时效行为[J].金属热处理,2010,35(7):54-57.

Chen Guohui,Zhang Xiaocong,Lou Chengping,et al.Aging Behavior of PH15-7Mo Precipitation-hardening Stainless Steel[J].Heat Treatment of Metals,2010，35(7)：54-57.

[15]庄茁,由小川,廖剑晖,等.基于ABAQUS的有限元分析和应用[M].北京:清华大学出版社,2009.

[16]赵腾伦,姚新军.ABAQUS 6.6在机械工程中的应用[M].北京:中国水利水电出版社,2007.

(编辑张洋)

Three-dimensional FEA of Manufacturing Process of Small-diameter Split Sleeve by Two-axle Bending

Gong JingpingLi XiangfengZuo DunwenKang XiaojunQiu Jiabin

Nanjing University of Aeronautics & Astronautics,Nanjing,210016

Based on the two-axle bending technique,a three-dimensional FEA was developed for the manufacturing process of small-diameter split sleeve of 0Cr15Ni7Mo2Al,in order to guide the actual manufacture of the small-diameter split sleeve.The model was verified with two-axle bending experiments.Stress strain distribution,deformation of rigid axle,the relationship among rigid axle diameter,workpiece size and curvature radius were analyzed.The simulation results show that workpiece deforms more equally with the increases of feed.The force of rigid axle becomes smaller with the increase of diameter,while deformation of rigid axle becomes lager with the decrease of diameter.The curvature radius increases with the increase of rigid axle diameter.The curvature radius increases with larger width and thickness of workpiece.

finite element analysis(FEA);smmall-diameter split sleeve;two-axle bending;0Cr15Ni7Mo2Al;cold extrusion

2014-05-21

空装十一五项目;中央高校基本科研业务费专项资金资助项目(kfjj130118);南京航空航天大学2013年度研究生创新基地(实验室)开放基金资助项目(kfjj130118)

TG306DOI：10.3969/j.issn.1004-132X.2015.08.022

龚靖平,女,1989年生。南京航空航天大学机电学院硕士研究生。主要研究方向为抗疲劳制造。发表论文2篇。黎向锋,女,1971年生。南京航空航天大学机电学院教授。左敦稳,男,1964年生。南京航空航天大学机电学院教授、博士研究生导师。康晓军，男，1988年生。南京航空航天大学机电学院硕士研究生。邱佳斌，男,1988年生。南京航空航天大学机电学院硕士研究生。