大型直缝焊管预弯成形工艺稳健性设计

范利锋　高　颖　云建斌　白宇杰

1.内蒙古大学,呼和浩特,010070　　2.河北科技大学,石家庄,0500183.内蒙古质量技术检验研究院,呼和浩特,010070

大型直缝焊管预弯成形工艺稳健性设计

范利锋1高颖2云建斌3白宇杰1

1.内蒙古大学,呼和浩特,0100702.河北科技大学,石家庄,0500183.内蒙古质量技术检验研究院,呼和浩特,010070

为提高预弯成形质量,采用有限元法分析了预弯成形过程,并验证了计算结果的准确性。在此基础上,考虑板料的材料性能参数等不确定因素对成形质量的影响,并基于随机模型的稳健性设计方法获得了预弯成形技术参数的稳健性优化设计方案。研究结果表明:稳健性优化使成形质量的性能指标得到了改善,将可靠性由4.2%提高到97.7%,显著提高了焊管成形质量可靠性。

大口径直缝焊管;预弯;有限元分析;稳健性

0　引言

预弯成形工艺广泛应用于大口径直缝焊管的制造,即通过预弯模具对钢板两边边缘进行压力成形，将板边弯曲成一定曲率，使之接近或达到管坯公称曲率，从而保证最终制品焊缝区域的几何形状和尺寸精度。该工艺有效地防止了焊缝“噘嘴”和扩径时开裂[1-2]。

预弯成形工艺的重要性促使国内外学者针对其进行了大量研究。文献[3-5]分析了预弯成形过程,文献[4,6-7]分析了预弯成形质量对后续工艺质量或焊管质量的影响。但目前的研究均没有考虑板料材料性能参数等不确定因素对成形质量的影响。随着高钢级管线钢的应用，预弯成形力和回弹大幅提高[8],管线钢材料性能的不稳定对预弯成形质量的影响已不能忽视。

因此，本文采用有限元方法对预弯成形过程进行分析，以仿真结果为输入样本点，构建了基于径向基函数的预弯成形近似模型，设计了稳健性优化数学模型，并使用遗传算法、灰色关联分析等方法获得了预弯成形的稳健性优化设计方案，以提高焊管预弯成形质量稳定性。

1　预弯成形过程分析

1.1预弯成形基本理论

板料预弯时,凸模通常是固定的，油缸驱动凹模逐渐上升，板料从坐标原点O点开始沿凸模型面逐渐发生弯曲变形,包覆凸模型面后，于A点结束。A点到板边的板料变形可忽略,近似认为此段为直边。此时A点法线方向与垂直方向的夹角为预弯卷角α,如图1所示。

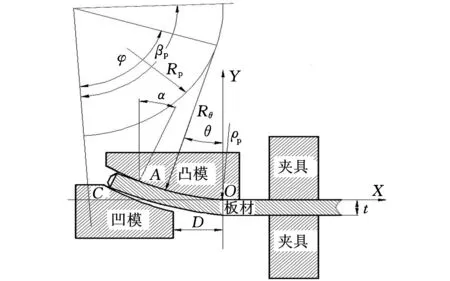
图1　预弯成形过程

预弯凸凹模型面曲线均采用渐开线设计,由于渐开线方程可表示为

(1)

式中,Rp为基圆半径,mm；φ为基圆角度,rad。

以O点为原点建立坐标系OXY,则该预弯凸模型面曲线在直角坐标系OXY下的参数方程为

(2)

式中,βp为终止角度,rad。

根据渐开线性质，可得渐开线基圆角度φ与板料变形段任一点预弯卷角θ和凸模曲率半径Rθ的关系：

(3)

则预弯凹模与板料接触点(C点)坐标为

(4)

式中,φA为A点所对应的基圆角度，rad;LZ为直边长度,mm。

由变形前后中性层长度不变和几何关系可得：

LZ=B-RPα(βP-α/2)-ttanα/2-P

(5)

式中，t为板料厚度，mm；B为预弯长度,mm;P为坡口宽度,mm。

预弯凹模型面曲线可由预弯凸模型面曲线(式(2)所示曲线)平移可得：

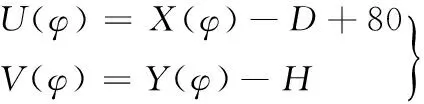
(6)

式中,D为凸凹模水平间距,mm;H为凸凹模垂直间距,mm。

根据式(2)、式(4)、式(6)和图1所述几何关系,分别以加载开始时和终止时,凹模与板料接触点(C点)坐标值相等为条件,可得下式：

(7)

式中,φ0、φt分别为加载开始和加载终止时预弯凹模C点对应的基圆角度。

由式(7)可得加载终止时凸凹模垂直间距H′和加载开始时凸凹模垂直间距H0。因此,预弯凹模位移为

h=H0-H′

(8)

根据大口径焊管成形特点，板边预弯部分所对管坯的圆心角为

(9)

式中,Rn为管坯的公称外半径，mm。

直边所对的管坯圆心角为

(10)

因此,板料回弹后预弯目标卷角αt为

αt=α′-α″

(11)

实际生产过程中，预弯卸载后，板料发生回弹，回弹后预弯卷角αY应无法保证等于预弯目标卷角αt,所以定义ΔαY=αY-αt来衡量预弯角的质量。为进一步衡量预弯成形后板边变形曲率半径分布状况，定义等效曲率半径:

(12)

等效曲率半径愈逼近于公称曲率半径，预弯成形质量越好。因此,可定义等效曲率半径R′与公称曲率半径R之差ΔR来评价预弯成形后板边曲率半径的质量。

综上所述,可得影响预弯成形的主要参数：凸模基圆半径Rp、凸模终止角度βp、垂直成形力Fy和预弯长度B。

1.2预弯成形有限元分析

对于预弯这种典型的宽板弯曲模式，宽度方向应变远远小于其他方向的应变，因此可忽略宽度方向变形，建立二维平面应变有限元模型。设置板料为二维可变形实体，其单元为四节点平面应变减缩积分四边形单元CPE4R(单元长度为2mm)。模具由于具有较高的刚度和硬度，故不考虑模具变形，将预弯凸模、凹模设置为离散刚体,采用R2D2刚体单元(单元长度为2.5mm)。夹紧模具具有简单几何形状的零件，可设置为不需要划分网格的解析刚体，如图2所示。

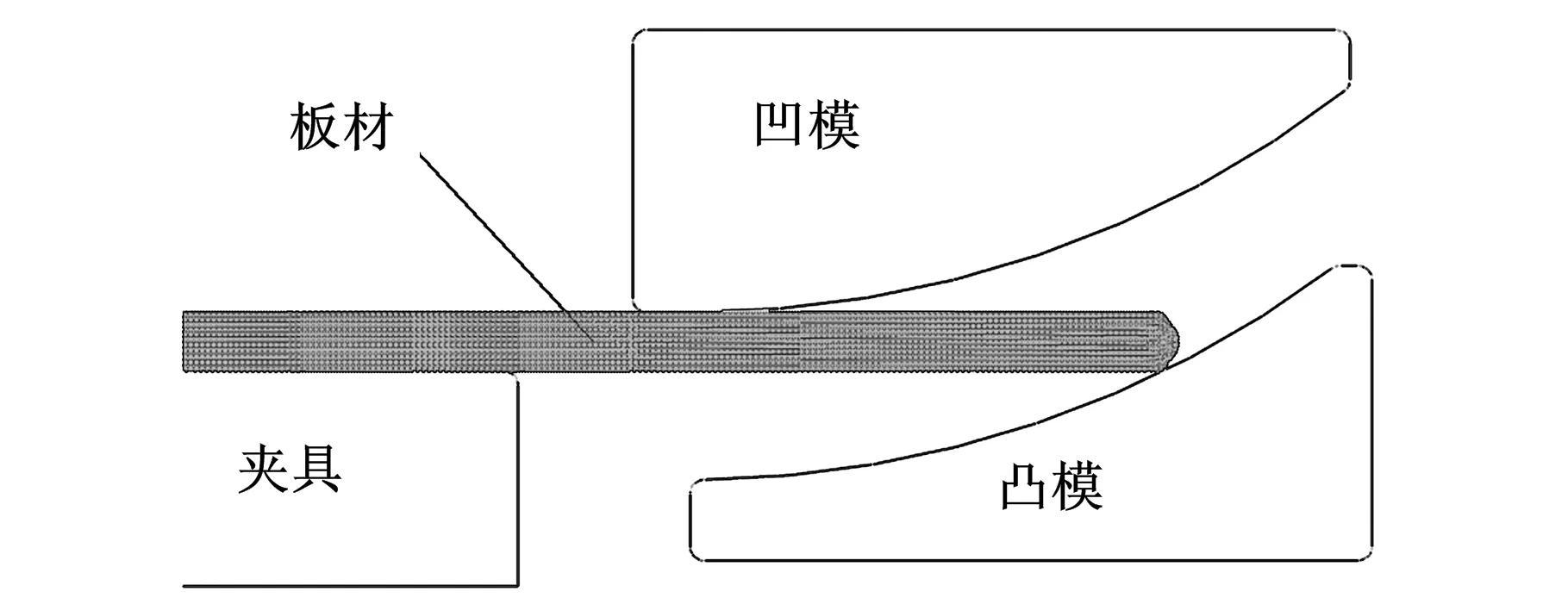
图2　预弯成形有限元模型

本文选用计算回弹精度较高的静态隐式算法对预弯成形过程进行仿真，选取单纯的有限滑动主从接触算法，模具为主面，板料为从面。利用罚函数摩擦模型(其中的摩擦因数为0.1)判断主从面的接触状态，主从面之间允许发生弹性滑动的同时，主面也可以在从面的节点间侵入，从而不增加系统的自由度，提高有限元模型计算效率。

以Q235A为实验材料进行预弯成形实验，如图3所示。采用三坐标测量仪测量预弯成形加载前后板料上表面的外形，并与有限元分析结果比较(图4～图5)。研究结果表明有限元模型能够准确预测管坯外形。

图3　预弯成形实验过程

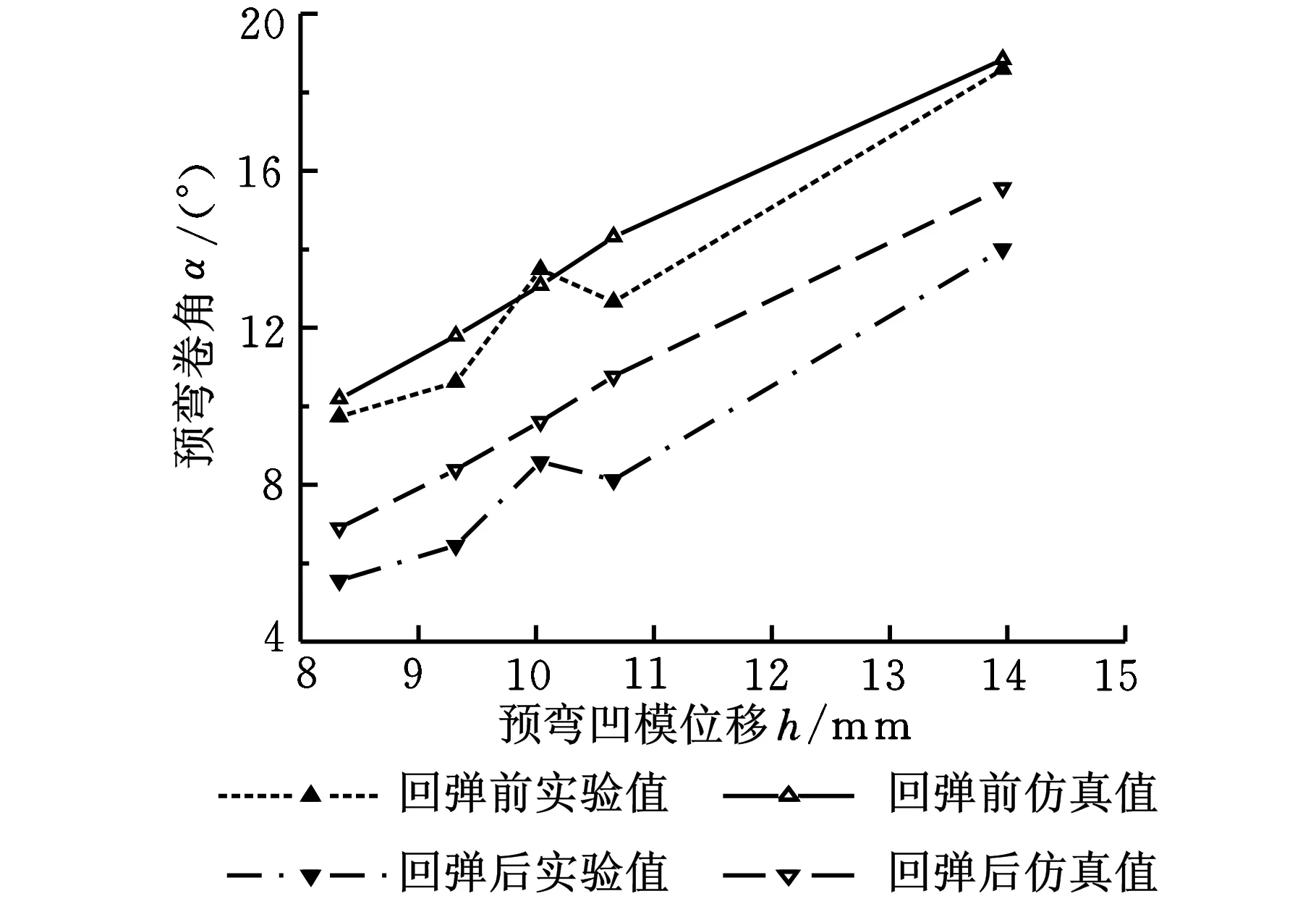
图4　凹模行程与预弯卷角关系

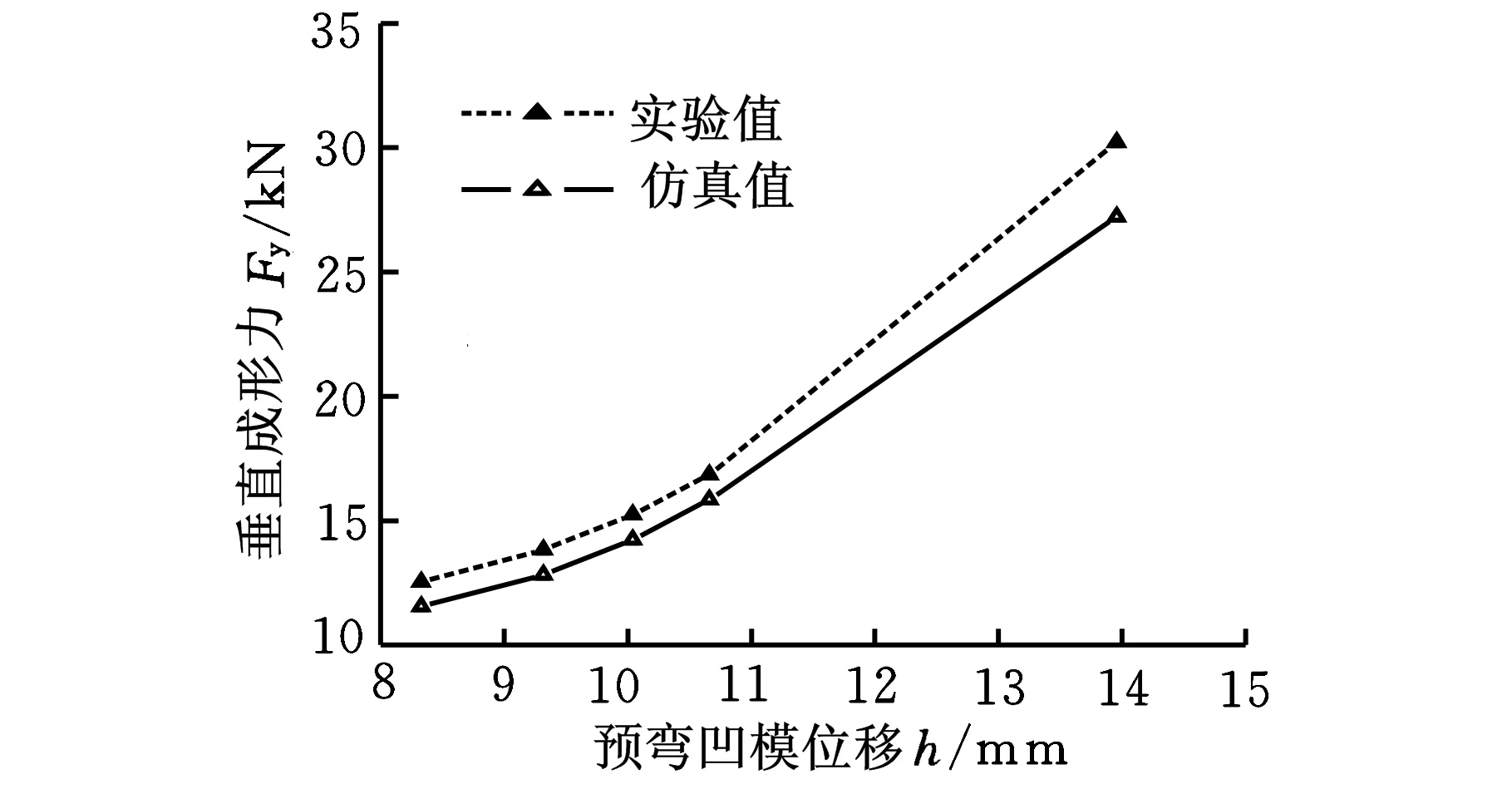
图5　凹模行程与最大成形力关系

由图4、图5可知,仿真结果与实验结果存在一定误差，随着凹模位移的增加，成形力误差明显增大。误差原因主要有两个，其一是预弯模具在制造和装配过程存在一定误差,与有限元模型不符；其二是随着凹模位移的增加,成形力受凹模位移的影响敏感性增大，其凹模位移和成形力的测量误差将使图5中的误差放大。

2　预弯成形近似模型

实际的优化设计过程中,往往需要考虑多个优化目标，且多个优化目标在给定的约束条件下都要尽可能接近理想状态。这一过程需要成千上百次的搜索计算，而采用实验和有限元分析的方法是无法满足这一要求的。采用基于径向基函数的近似模型能够缩短其分析时间，降低问题的非线性，便于找到优化点。本文采用径向基函数构建响应面模型,其一般步骤如下:①按照田口试验设计方法进行样本设计;②使用回归拟合的方法获取近似函数y=f(x);③按照常用的响应面模型误差指标分析预弯成形径向基函数响应面模型模的精度。

首先,采用概率统计的方法分析一批X80管线钢材料性能参数分布状况。X80管线钢材料性能参数符合正态分布。因此，计算其标准差和平均值，如表1所示。

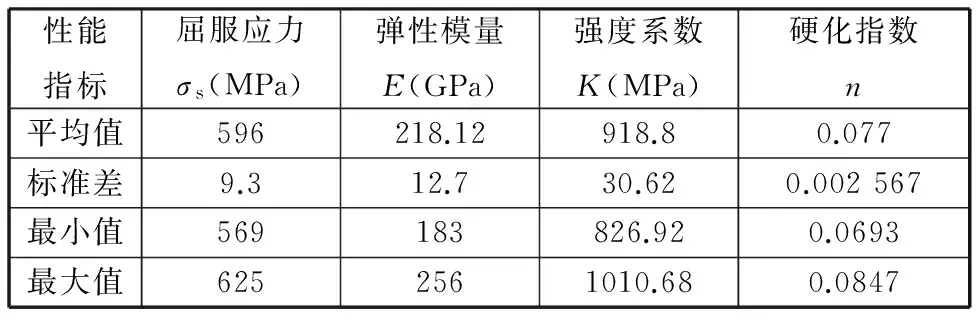
表1　X80管线钢材料性能参数及其波动性

田口内外表试验设计法是将可控因素和不可控因素安排在同一个试验表中。其中，可控因素的设计表作为内表,不可控因素的设计表作为外表，以直积的形式交叉排列。本文采用L9(34)的正交试验设计方案安排外表(表2)。采用优化拉丁方试验设计方案安排内表(表3)。

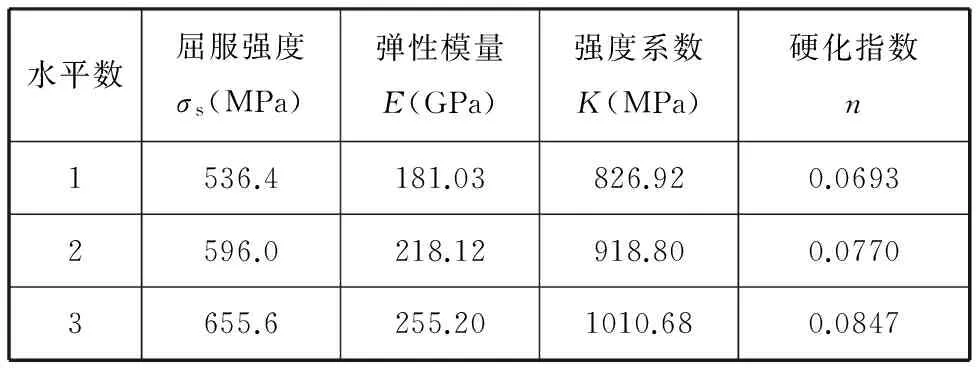
表2　外表材料性能参数水平数

表3　预弯技术参数内表设计方案

以内外表直积法仿真结果作为样本点，构建基于径向基函数预弯响应面模型。该响应面模型能够反映包含材料参数和工艺参数在内的影响因素与成形质量性能指标的映射关系，通过常用误差评估指标评估响应面模型的估计精度，见表4。

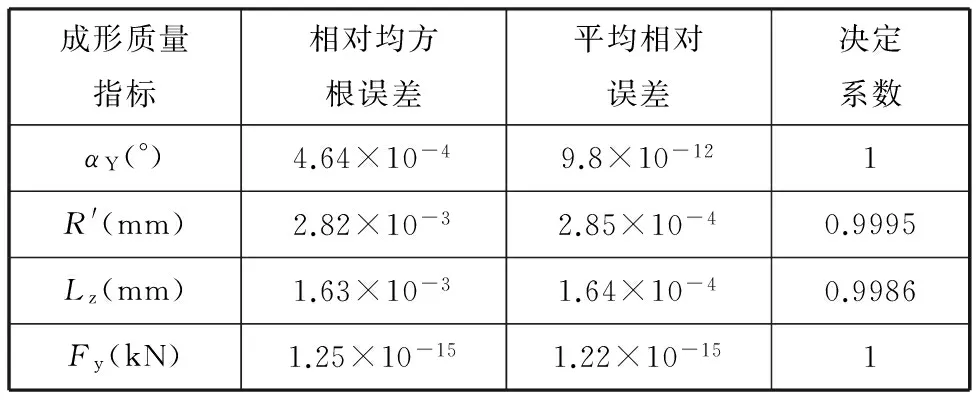
表4　预弯成形径向基函数响应面模型的误差分析

由表4可知，相对均方根误差和平均相对误差都很小，其中最大值仅为2.82×10-3,且各成形质量的决定系数接近于1。这表明预测模型所表达的超曲面通过大部分样本点，预测模型拟合精度较高，可以作为真实问题的替代模型。

3　基于随机模型的稳健性设计

根据稳健性设计原理，按照预弯成形的实际工况建立稳健性优化数学模型，采用遗传算法在其参数设计空间进行迭代搜索，利用蒙特卡罗模拟抽样计算焊管质量指标的方差和均值，根据优化数学模型获取稳健性Pareto解集，对其进行灰色关联分析以得到稳健性最优方案。稳健性优化流程如图6所示。

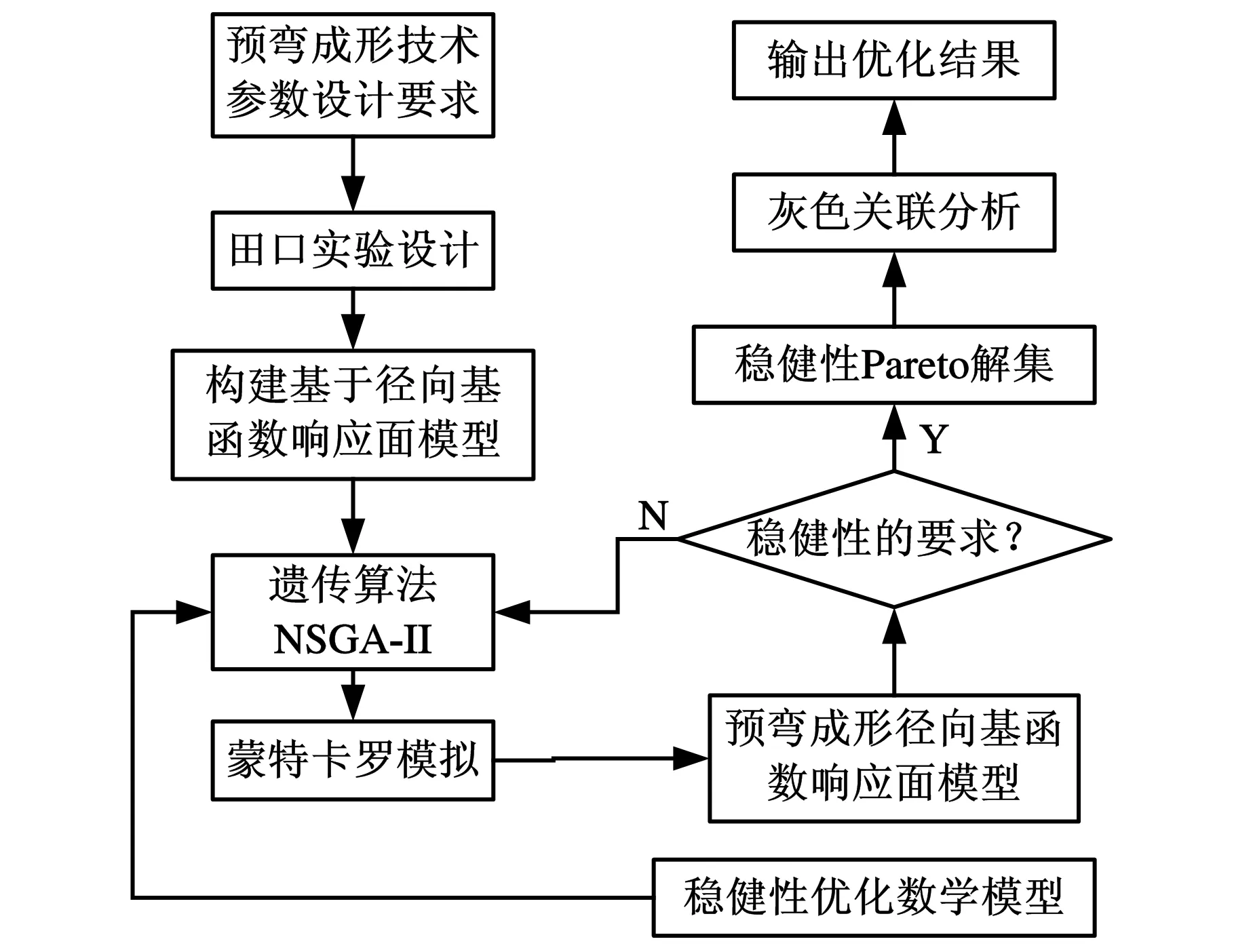
图6　稳健性优化设计流程图

典型的稳健性优化公式既要优化目标的均值和标准差,又要满足约束的波动边界。从工程应用观点出发，采用以下的稳健设计模型：

minf1(μ[Lz],σ[Lz])=μ[Lz]+6σ[Lz]

f2(μ[ΔR],σ[ΔR])=μ[ΔR]+6σ[ΔR]

(13)

s.t. G1(μ[Lz],σ[Lz])=μ[Lz]+6σ[Lz]≤33

G2(μ[ΔR],σ[ΔR])=μ[ΔR]+6σ[ΔR]≤15

H1(μ[ΔαY],σ[ΔαY])=μ[ΔαY]+6σ[ΔαY]≤ε

基于6σ的稳健性设计优化即是将n设定为6,稳健性优化设计目标公式中，μ[*]、σ[*]分别表示物理量的均值和标准差(由蒙特卡罗模拟技术计算得到)。等式约束中的ε=1°。

本文采用遗传算法和蒙特卡罗模拟求取Pareto稳健性优化解集。其中,遗传算法的初始种群为8,交叉概率为0.65,变异概率为0.1,遗传代数为200,抽样方法是描述性抽样，抽样次数为200。

4　基于灰色关联分析的参数方案决策

为了从Pareto稳健性优化解集中筛选出最优方案，本文采用灰色关联分析的方法，挑选出Pareto最优解集中工艺方案与理想工艺方案的灰色关联度最大的方案(该方案与理想值最为接近，即为最优方案)，从而达到决策的目的。

灰色关联分析的一般步骤如下：①确定参考序列和比较序列；②数据的量纲一化；③求解灰色关联系数；④求解灰色关联度；⑤灰色关联度排序。

比较序列作为与参考序列相比较的子序列，通常由多目标优化Pareto解集中各组优化解集组成。参考序列则是以不同优化目标为优化方向的单目标最优值,记为x0j。因此，以成熟的序列二次规划法为单目标优化算法，分别搜索第一目标函数和第二目标函数在约束条件下的优化解。以φ1219 mm×22 mm×12000 mm焊管为例，第一目标函数初始点为f1=60,经过81次迭代收敛于8.9。第二目标函数初始点为f2=2.49,经过82次迭代收敛于0.005。可确定预弯成形的参考序列为(8.9,0.005)。同时选取Pareto前沿方案作为比较序列。

首先将比较序列xi和参考序列x0按照当目标具有望小特征的数据处理公式进行归一化，即可通过如下式可得处理后数据：

(14)

然后计算比较序列xi对于参考序列x0在第k个目标下的灰色关联系数：

ξi(k)=

(15)

式中,ρ为分辨系数,ρ=0.5436。

需要考虑全部优化目标情况下的关联水平,取关联系数的平均值作为比较全过程的关联程度的度量：

(16)

其中,λk为加权系数，采用群体评估法计算权系数，其评估结果如表5所示。通过计算可得预弯成形权系数λ1=0.518 685,λ2=0.481 315。

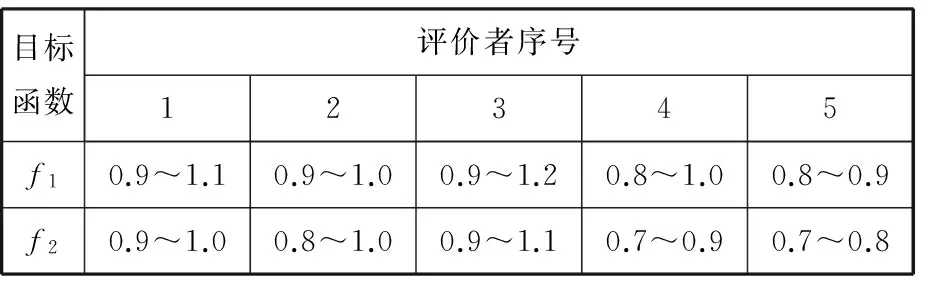
表5　预弯成形优化目标评价结果

最后,需要对灰色关联度排序。灰色关联度最大的比较序列即为Pareto解中与理想状态最为接近的多目标稳健性最优解。

5　稳健性优化结果分析

将φ1219 mm×22 mm×12000 mm焊管预弯变形过程原设计方案和稳健性优化设计方案进行对比，分析其优化结果和可靠性，如表6所示。

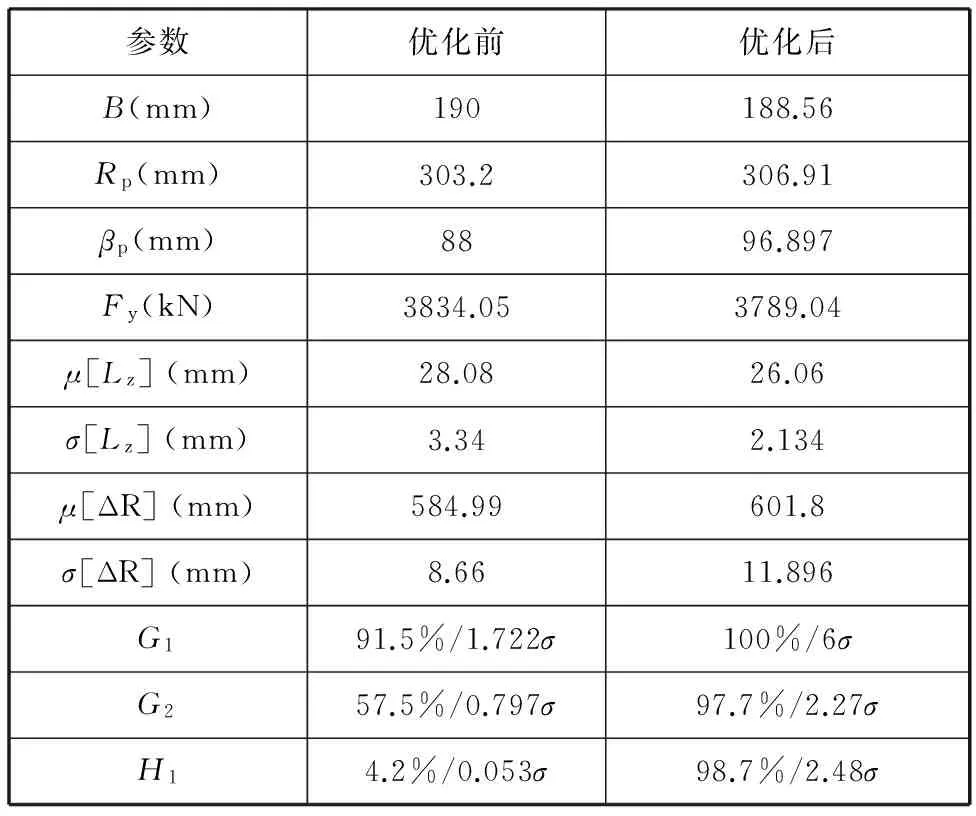
表6　稳健性优化前后的设计结果

由表6可知,相对原设计点而言，稳健性优化结果不但使成形质量性能指标得到了改善，而且其可靠性由4.2%提高为97.7%。目前,预弯稳健性优化结果仍不能达到6σ水平,只能达到2.48σ水平。这是由于优化模型中存在等式约束，其中允许误差范围仅为ε=1°,约束条件苛刻造成预弯成形稳健性优化结果无法达到6σ水平。

6　结论

(1)基于ABAQUS建立预弯成形工艺的有限元分析模型，分析了预弯成形过程。

(2)稳健性优化设计不但改善预弯成形质量，而且将预弯成形质量可靠性提高到97.7%。

[1]严圣祥,钟情霞.我国应发展大口径直缝焊管技术[J].钢铁,2001,36(5):73-76.

Yan Shengxiang,Zhong Qingxia.Developing Straight Welding Technology for Large Diameter Pipe in China[J].Iron and Steel,2001,36(5):73-76.

[2]李宏.直缝埋弧焊钢管生产线预弯工艺[J].焊管,2006,29(1):55-57.

Li Hong.Prebending Process of Longitudinal Submerged Arc Welding Production Line[J].Welding Pipe,2006,29(1):55-57.

[3]谢志民,夏金明.直缝埋弧焊管预弯工艺参数设计[J].焊管,2007,30(3):52-54.

Xie Zhimin,Xia Jinming.Prebending Process Parameter Design of Longitudinal Submerged Arc Welding Pipe[J].Welding Pipe,2007,30(3):52-54.

[4]Herynk M D,Kyriakides S,Onoufriou A,et al.Effects of the UOE/UOC Pipe Manufacturing Processes on Pipe Collapse Pressure[J].International Journal of Mechanical Sciences,2007,49(5):533-553.

[5]Palumbo G,Tricarico L.Effect of Forming and Calibration Operations on the Final Shape of Large Diameter Welded Tubes[J].Journal of Materials Processing Technology,2005,164/165(5):1089-1098.

[6]刘京雷,黄克坚,阮锋.预弯工艺参数对UOE焊管O成形的影响[J].塑性工程学报,2005,12(3):72-75.

Liu Jinglei,Huang Kejian,Ruan Feng.Effects of the Parameters of Prebending on O-forming of Pipe in UOE Process[J].Journal of Plasticity Engineering,2005,12(3):72-75.

[7]全晓刚.UOE焊管坡口形状与引弧板开口角研究[D].秦皇岛:燕山大学,2008.

[8]孙红磊,宋晓抗,马瑞,等.大型直缝焊管四点弯曲JCO成形及其弹复解析[J].中国机械工程,2014,25(2):257-262.

Sun Honglei,Song Xiaokang,Ma Rui,et al.Theoretical Analysis of JCO Forming and Springback for Sheet Metal Four-point Bending in Manufacture of LSAW Pipe[J].China Mechanical Engineering,2014,25(2):257-262.

(编辑张洋)

Robustness Design for Crimping of Large Diameter Straight Welded Pipe

Fan Lifeng1Gao Ying2Yun Jianbin3Bai Yujie1

1.Inner Mongolia University,Hohhot,010070 2.Hebei University of Science and Technology,Shijiazhuang,050018 3.Product Quality Inspection Institute of Inner Mongolia,Hohhot,010070

To improve crimping forming quality,this paper investigated crimping which was simulated using the FE code ABAQUS and the FE model was validated experimentally.Based on this analysis,robustness design method based on stochastic model was used to obtain optimization design scheme,which considered the effects of uncertain factors such as material performance parameters on the forming quality.The research results show that the optimization design scheme can improve the product performance,and increase the reliability from 4.2% to 97.7% and ensure the product quality.Thus, the results herein provide an effective approach for crimping parameter design.

large diameter straight welded pipe;crimping;finite element analysis(FEA);robustness

2014-05-07

内蒙古大学高层次人才引进项目(135143);内蒙古高等学校科学研究项目(NJZY14006);河北省高等学校科学技术研究青年基金资助项目(Y2012035)

TG386< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.08.021

范利锋,男,1982年生。内蒙古大学交通学院讲师、博士。主要研究方向为数值模拟、塑性成形、焊管制造技术。高颖,女,1973年生。河北科技大学材料科学与工程学院副教授、博士。云建斌,男,1981年生。内蒙古质量技术检验研究院工程师。白宇杰，女,1981年生。内蒙古大学交通学院实验员。