基于粒子群算法的滑阀节流槽优化设计

李维嘉　兰秋华　彭　勇　易迪升

1.华中科技大学,武汉,430074　　2.三一汽车起重机械有限公司,长沙,410000

基于粒子群算法的滑阀节流槽优化设计

李维嘉1兰秋华1彭勇2易迪升2

1.华中科技大学,武汉,4300742.三一汽车起重机械有限公司,长沙,410000

基于Fluent流场仿真分析软件,在定压差条件下,对带有单U形、斜U形以及V形基本节流槽的滑阀阀口开度-流量特性开展了研究,并将其与试验结果进行了对比验证,得出了U形类槽口随着阀口开度的增加流量梯度减小、斜U形类槽口随着阀口开度的增加基本保持不变、V形类槽口随着阀口开度的增加流量梯度增大的结论。基于上述研究,利用粒子群优化算法,得到满足定压差条件下阀口开度-流量特性要求的节流槽优化尺寸,并通过实例验证了优化结果。

节流槽;优化设计;流量特性;粒子群算法

0　引言

滑阀节流槽广泛应用于液压执行机构的主控阀阀芯中,其流量特性对执行机构运动品质起着关键作用。结构合理的节流槽能满足液压执行执行机构在启动及停止等不同工况下的流量要求,且能实现小流量时复杂的流量控制,具有好的稳定性,减小振动,提高整个执行操作系统的舒适度。国内外学者对节流槽的研究主要集中在过流面积特性[1]、流量系数特性[2-3]、液动力静态特性[4-5]以及动态特性[6-7]等方面。虽然学者们对节流槽的认识逐渐清晰,但基于传统公式所得到的节流槽流量系数随着开度变化而出现较大、无规律波动,导致节流槽的设计过程过多依赖于设计者的经验。由于节流槽的设计往往需要经过多次估算、加工、测试，使得其设计过程复杂、设计成本偏高且浪费较大，因此开展节流槽的优化设计研究是必要的。

节流槽设计优化算法有传统的优化方法和智能优化算法，传统的优化方法包括坐标轮换法、复合型法等，智能优化算法包括遗传算法、粒子群优化算法[8-9]等。满足恒压工况下阀口开度-流量特性要求的节流槽优化设计，有着目标函数的状态未知、变量数不定、搜索空间恒定等特点，因此本文利用粒子群优化算法，结合部分节流槽的仿真计算值，针对常用的三种节流槽的优化设计，开展相关研究。

1　滑阀节流槽阀口开度-流量特性仿真研究

以单U形、斜U形和V形三种典型形式的滑阀节流槽(图1)为对象进行研究。研究中,选择的尺寸参数如表1所示,其中V形节流槽是由角度为60°的刀尖角切割而成。阀芯直径为28 mm,阀杆直径为16 mm。为了减少阀芯周向的不平衡对研究的影响,阀芯上沿周向对称分布有2个节流槽。表1中“-”代表无此项。

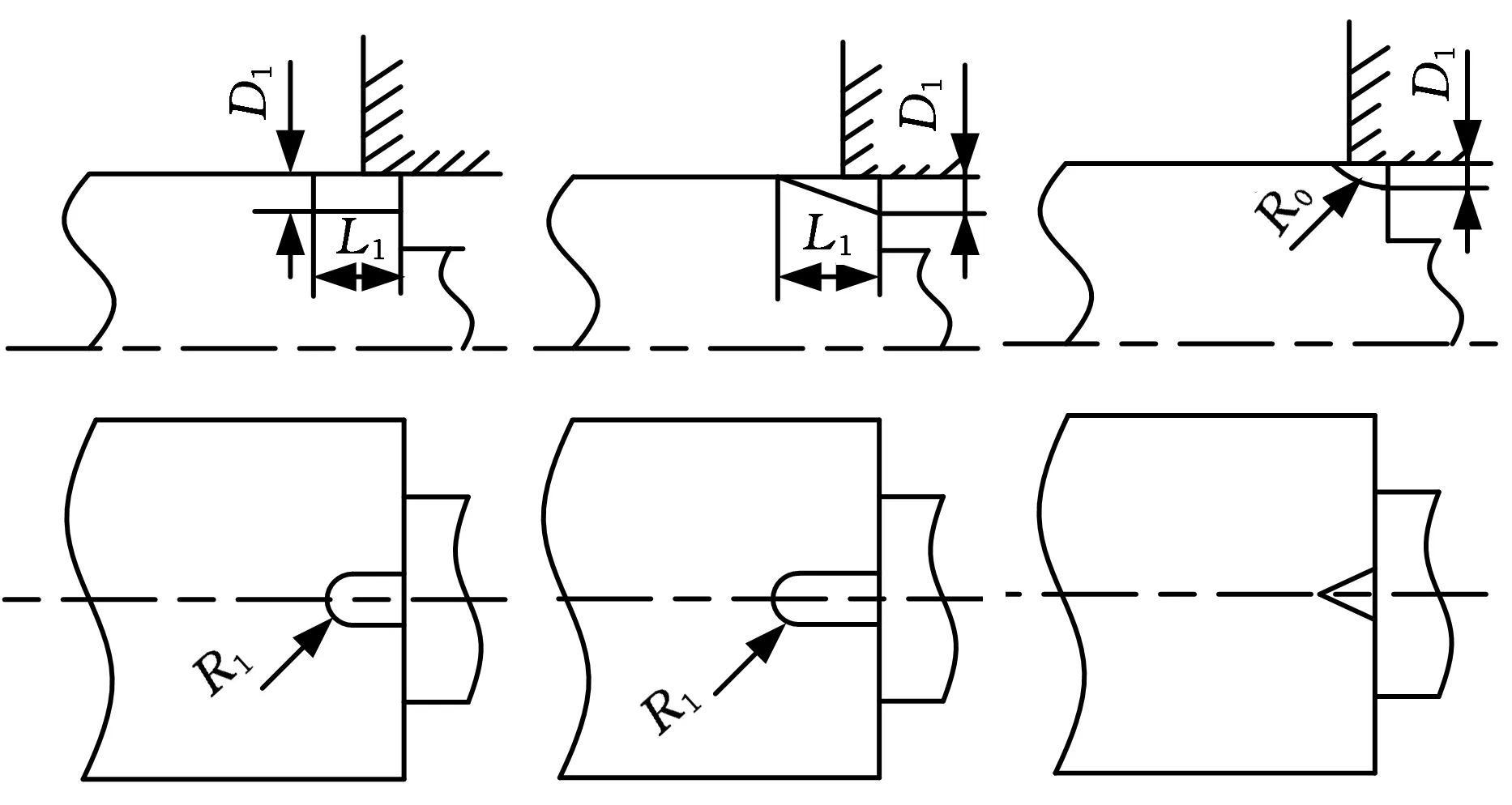
(a)单U形 (b)斜U形(c)V形图1　三种基本节流槽结构图

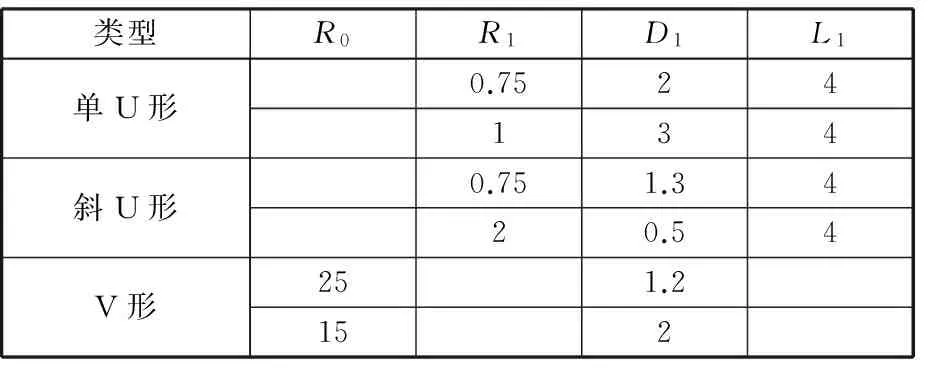
mm

基于表1中的滑阀节流槽尺寸参数,利用Solidworks三维设计软件,建立带有节流槽阀芯与阀体的装配体模型;利用CAE前处理软件ICEM(integrated computer engineering and manufacturing)对节流槽流道进行网格划分。图2所示为单U形节流槽口在开度为2 mm下的流道网格划分的模型。最后运用流体仿真分析软件Fluent,在定压差条件下，计算出滑阀节流槽在不同阀口开度时的流量。

图2　开度为2 mm时流场网格模型

仿真计算时选择标准的k-ε湍流模型;按照46号液压油的特质，将流体材质的密度设置为860 kg/m3,参考温度(40℃)下的黏性系数设置为0.038 25 kg/(m·s);设置压力进出口边界条件,进出口压差为1 MPa。三种形式节流槽在定压差工况下,各自的阀口开度-流量仿真计算特性如图3所示。

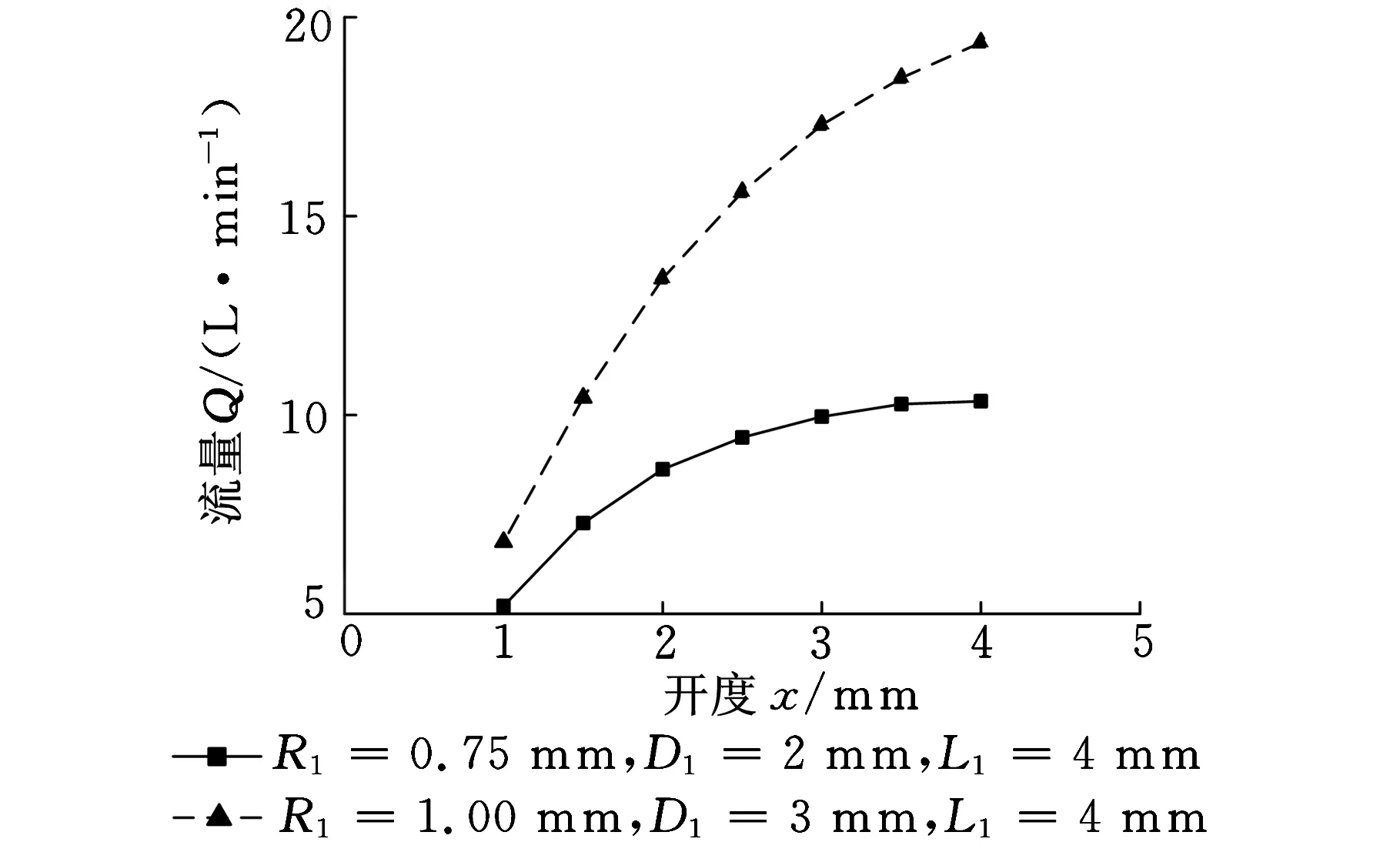
(a)单U形节流槽阀

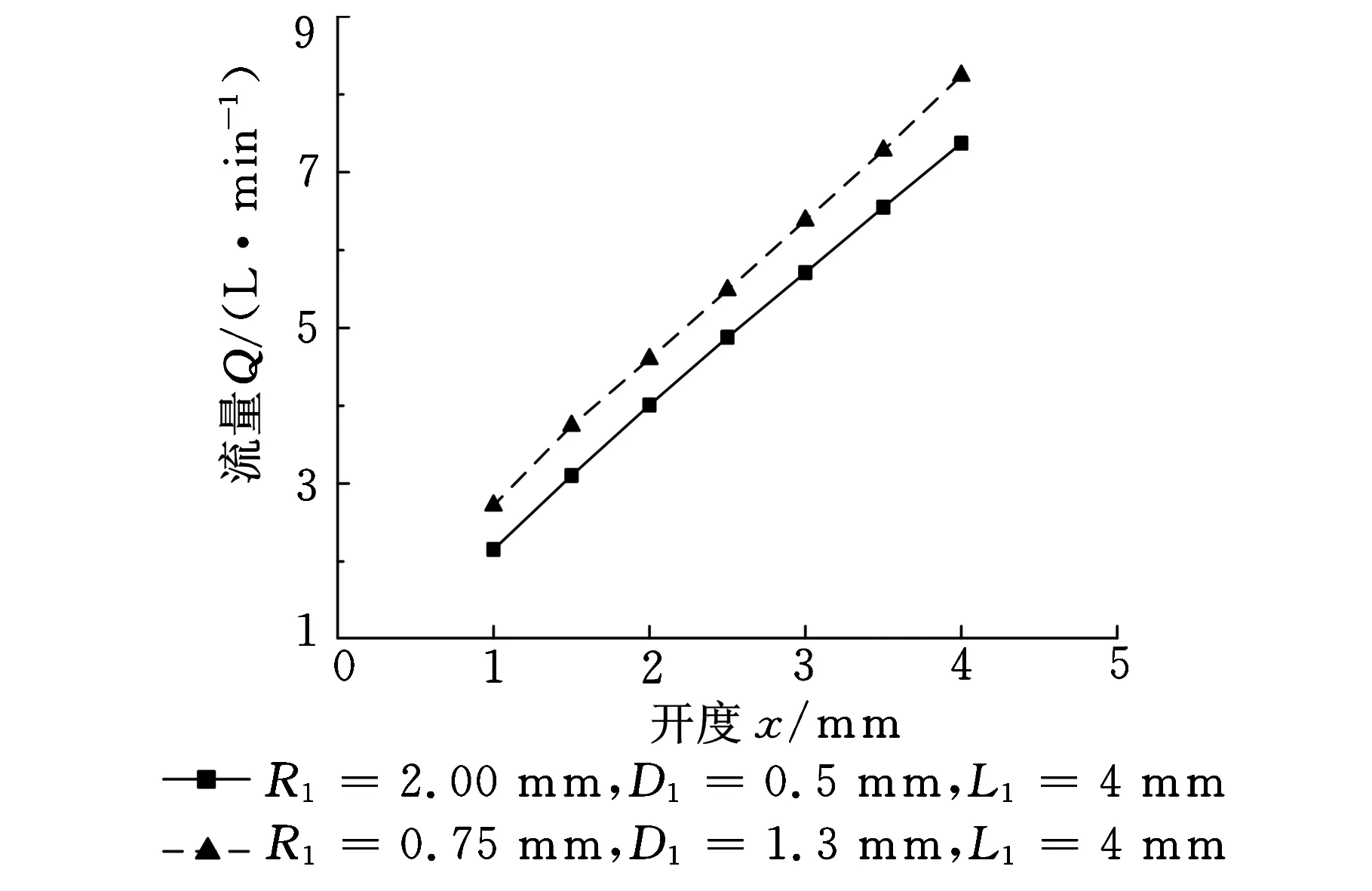
(b)斜U形节流槽阀

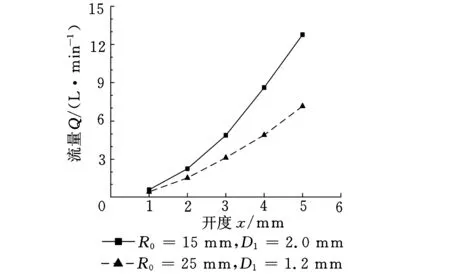
(c)V形节流槽阀图3　定压差下不同节流槽阀口开度-流量曲线仿真图

由图3可知,3种滑阀节流槽在定压差下的阀口开度-流量特性各不相同。随着阀口开度的增加,单U形节流槽流量梯度逐渐减小,V形节流槽流量梯度逐渐增大，斜U形的流量梯度趋于定值。

2　试验验证

图4是滑阀节流槽试验台原理图。用于试验验证的滑阀节流槽的尺寸参数如下:单U形滑阀节流槽中,R1=0.75 mm,D1=2 mm,L1=4 mm;V形滑阀节流槽中,R0=15 mm,D1=2 mm;斜U形滑阀节流槽中,R1=2 mm,D1=0.5 mm,L1=4 mm。负载部分用比例溢流阀模拟代替,通过调节电流大小获得所需负载大小。液压泵排量为180 mL/r,电机转速为1500 r/min,溢流阀设定值为7 MPa。在各个阀口处均安装有压力传感器,负载出口安装有流量传感器,以实现节流槽进出口的压力和流过槽口流量的测量。由文献[3]可知,流过节流槽的流量与节流槽进出口压差呈0.5次方关系。将试验中测试的阀口开度-流量特性转换为1 MPa压差下的阀口开度-流量特性,如图5所示。

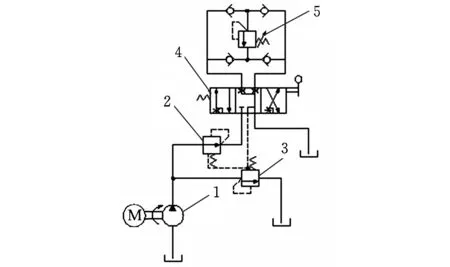
1.泵源　2.定差减压阀　3.定差溢流阀4.被试主阀　5.替代负载的比例溢流阀图4　试验台原理图

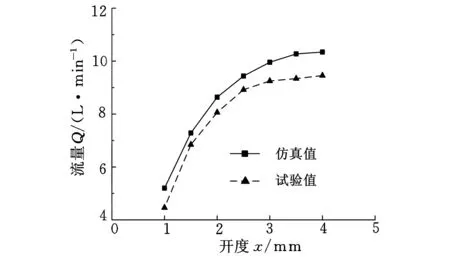
(a)单U形节流槽阀

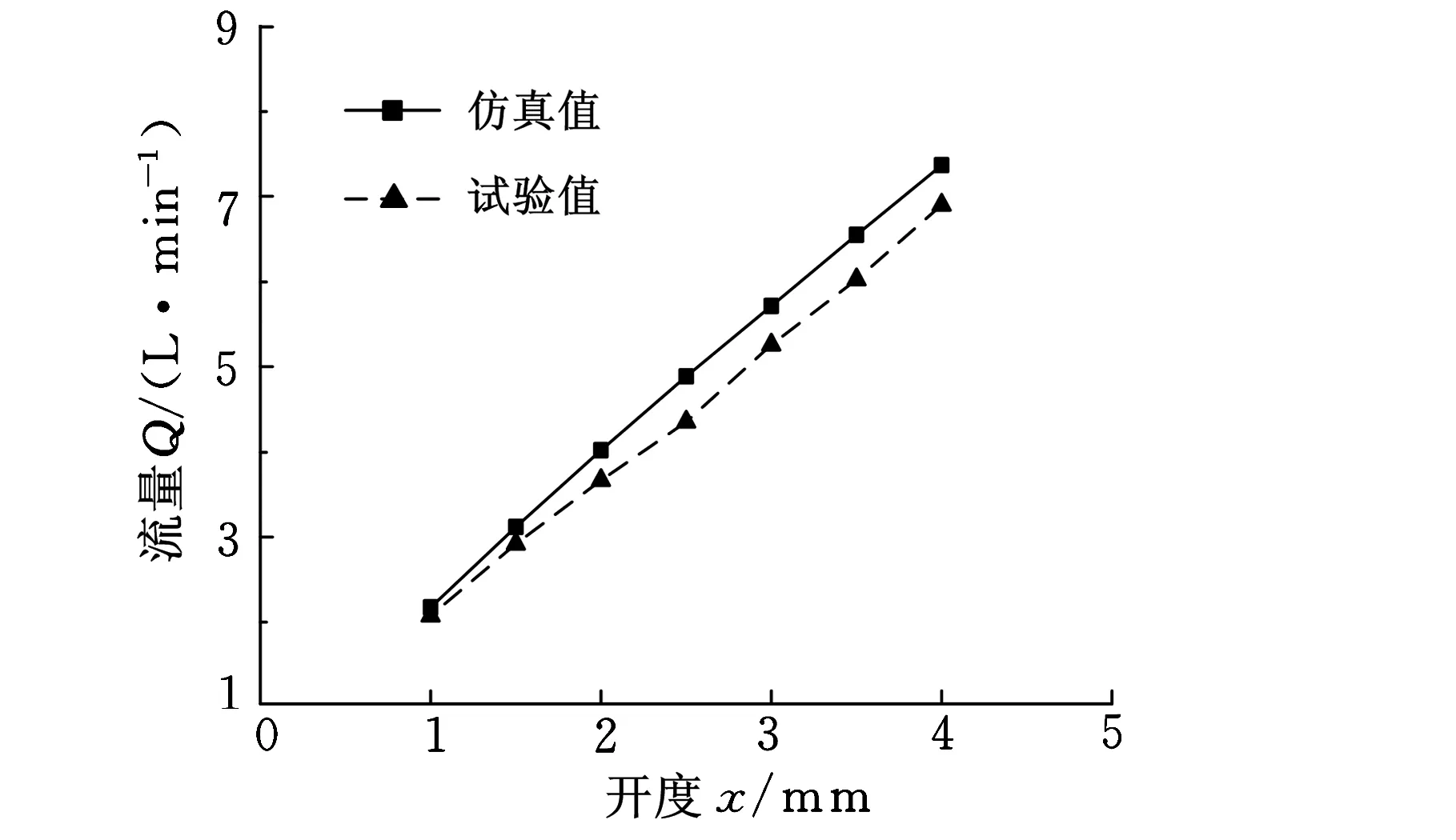
(b)斜U形节流槽阀

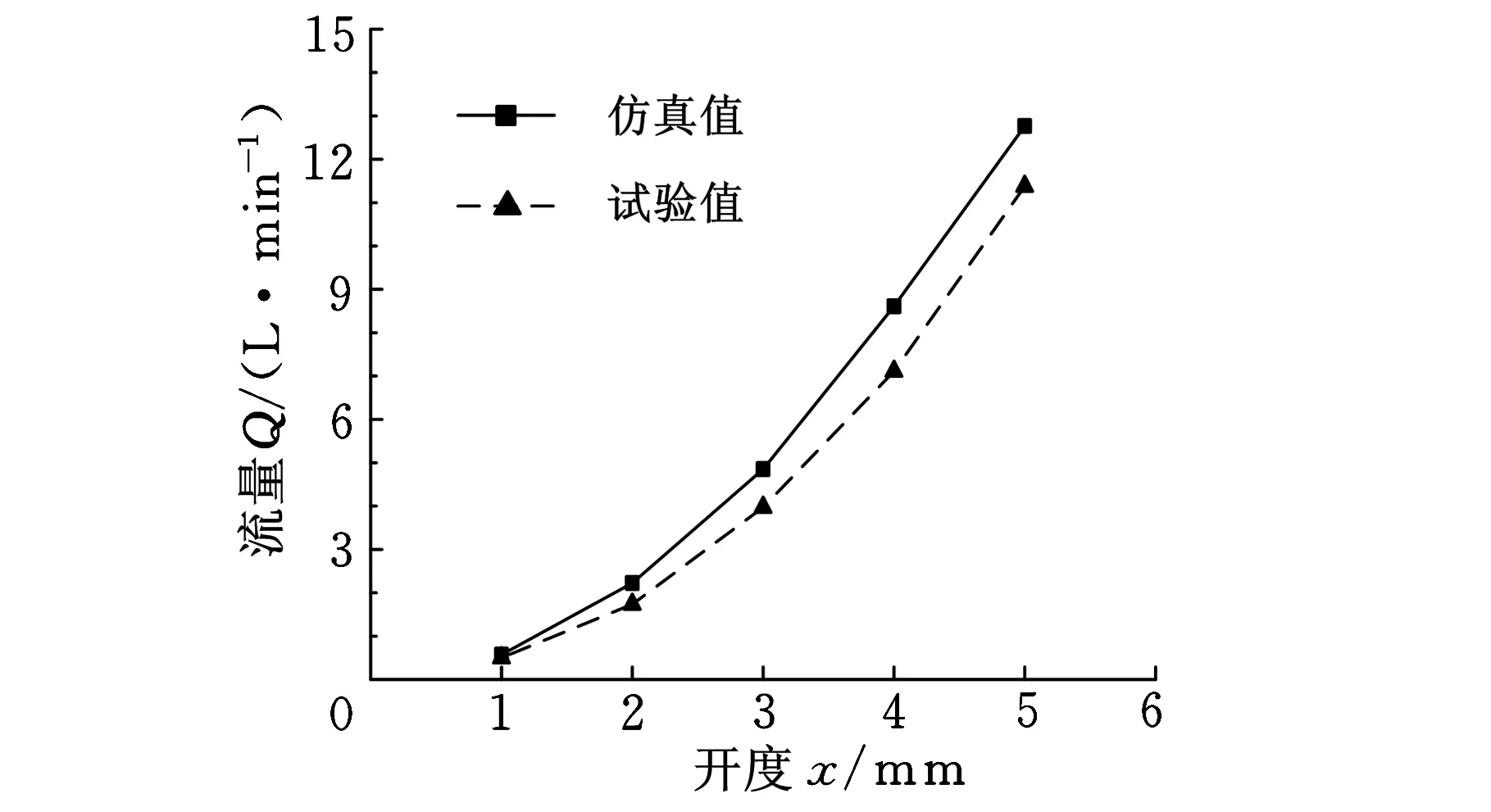
(c)V形节流槽阀图5　不同节流槽阀口开度-流量曲线的仿真与试验结果

由图5可知,3种节流槽阀口开度-流量特性的仿真值均与试验结果的趋势一致,且数值相近。仿真值虽然大于试验值,但误差在10%以内。造成误差的原因如下:①试验中,流量测试点选取在被试主阀与替代负载的比例溢流阀之间(图4),阀芯与阀套间会有一定的间隙，不可避免存在着内漏,使得测试值偏小;②测量仪器的精度与测试结果的读取都会造成误差。因此,基于Fluent的仿真计算结果是可信、比较准确的。

3　滑阀节流槽的优化

根据液压执行机构工作时对阀口开度-流量特性的要求,得到其对应滑阀节流槽的结构形状及节流槽结构尺寸参数，这一过程即为对滑阀节流槽的优化设计。根据定压差下的节流槽阀口开度-流量特性可知,先依据所需阀口开度-流量特性中的流量梯度判断节流槽的形状，再运用相应的优化算法进行优化设计就能得出希望的节流槽尺寸，即可完成优化过程，本研究选用粒子群算法完成对滑阀节流槽的优化设计。实际应用中，为保证液压系统的稳定，滑阀节流槽基本在定压差环境下工作，故本文都是基于定压差条件进行的研究，且所用到的仿真数据均是在1 MPa定压差下仿真计算所得的。

3.1优化原理

滑阀节流槽的优化中，首先定义节流槽的尺寸变量空间R。然后基于粒子群算法在节流槽变量空间内初始化多个粒子，形成种群，其中每个粒子对应着尺寸变量空间中的一个可行解，因此每个粒子在目标函数中都对应有一个值。目标函数值越优,粒子对应的解越优。之后，每个粒子在尺寸变量空间中运动，其运动速度受两个最优解(粒子本身的历史最优解pbest和全种群的历史最优解gbest)的影响，且粒子运动速度决定粒子运动的方向和距离。粒子种群的一次运动等效于算法的一次迭代，粒子运动遵循的规则，即算法遵循的迭代规则,可用数学公式描述为：尺寸变量为D维，粒子数(种群大小)为n，第i个粒子的在尺寸变量空间中的位置向量xi=(xi1，xi2，…，xiD)，速度矢量vi=(vi1，vi2，…，viD)，第i个粒子的历史最优解pbest,i=(pi1，pi2,…，piD),整个粒子群搜索到的历史最优解gbest,i=(g1,g2,…,gD)。粒子第k+1维的速度和位置的迭代公式为

(1)

(2)

其中,w为维持原速度的系数,叫做惯性权重;c1、c2为加速因子,c1具有调节粒子向自身最优位置移动的能力,代表了粒子对“自我”的认知;c2具有调节粒子向全局最优位置移动的能力,代表了粒子对“社会”的认知;ξ、η是[0,1]区间内均匀分布的随机数;r为约束因子;k为迭代次数。节流槽优化研究中,变量维数D为3,粒子数n=40,惯性权重w=0.7,加速因子c1=c2=2,迭代次数k=100。

3.2目标函数的建立

优化的目的,是在定压差条件下求出满足阀口开度-流量特性要求的节流槽最优尺寸,因此优化算法的解为尺寸向量X,其维数由尺寸变量个数D决定。因此根据需满足的阀口开度-流量特性,将目标函数定义为

(3)

式中,m为选取阀口开度-流量曲线中阀口开度点的个数;qj为第j个阀口开度点对应的已知流量;fj(X)为前期研究中流量与尺寸变量的函数关系;s为均方差。

均方差最小时,对应的可行解X为满足条件的最优解。

3.3优化过程

在优化过程中,定义矩阵[P]n×(2D+1)和[O](n+1)×D。[P]n×(2D+1)的每一行保存一个粒子的当前位置、速度与目标函数值,[O](n+1)×D前n行对应着[P]n×(2D+1)中每个粒子的历史最优位置,第n+1行对应着粒子种群的历史最优位置。首先在解空间范围内初始化矩阵[P]n×(2D+1),[O](n+1)×D随[P]n×(2D+1)而定。初始化后，每个粒子依照式(1)、式(2)进行迭代,在满足迭代要求的前提下将每次迭代后的粒子的位置、速度以及对应的适应度值保存在[P]n×(2D+1)内,每个粒子迭代出的最优适应值对应的位置以及所有粒子的最优位置保存在[O](n+1)×D中。迭代结束后,可在[O](n+1)×D的最后一行得到节流槽优化尺寸的最优解。3.4实例验证

若已知在1 MPa定压差条件下的某阀口开度-流量特性如图6所示。根据图6中流量梯度逐渐减小的趋势可以判断滑阀节流槽为单U形槽。选取阀口开度-流量特性中阀口开度x=[0.10.511.522.533.54](开度数组x中数值的单位为mm),以及对应的流量Q=[0.22.557.5910.211.011.511.9] (流量数组Q中数值的单位为L/min),带入算法中得到的最优解:R1=7.500 000×10-1mm;D1=2.436 380×100mm;最小均方差为1.518 655×10-2L/min。

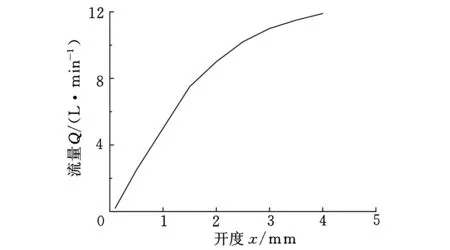
图6　需满足的阀口开度-流量特性曲线

图7所示为初始种群各个粒子的目标函数分布情况,图8～图10所示为各个粒子在迭代10次、50次、100次时目标函数分布情况。

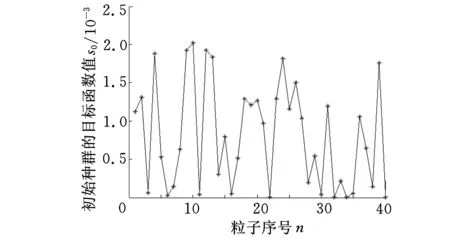
图7　初始种群中各个粒子的目标函数值

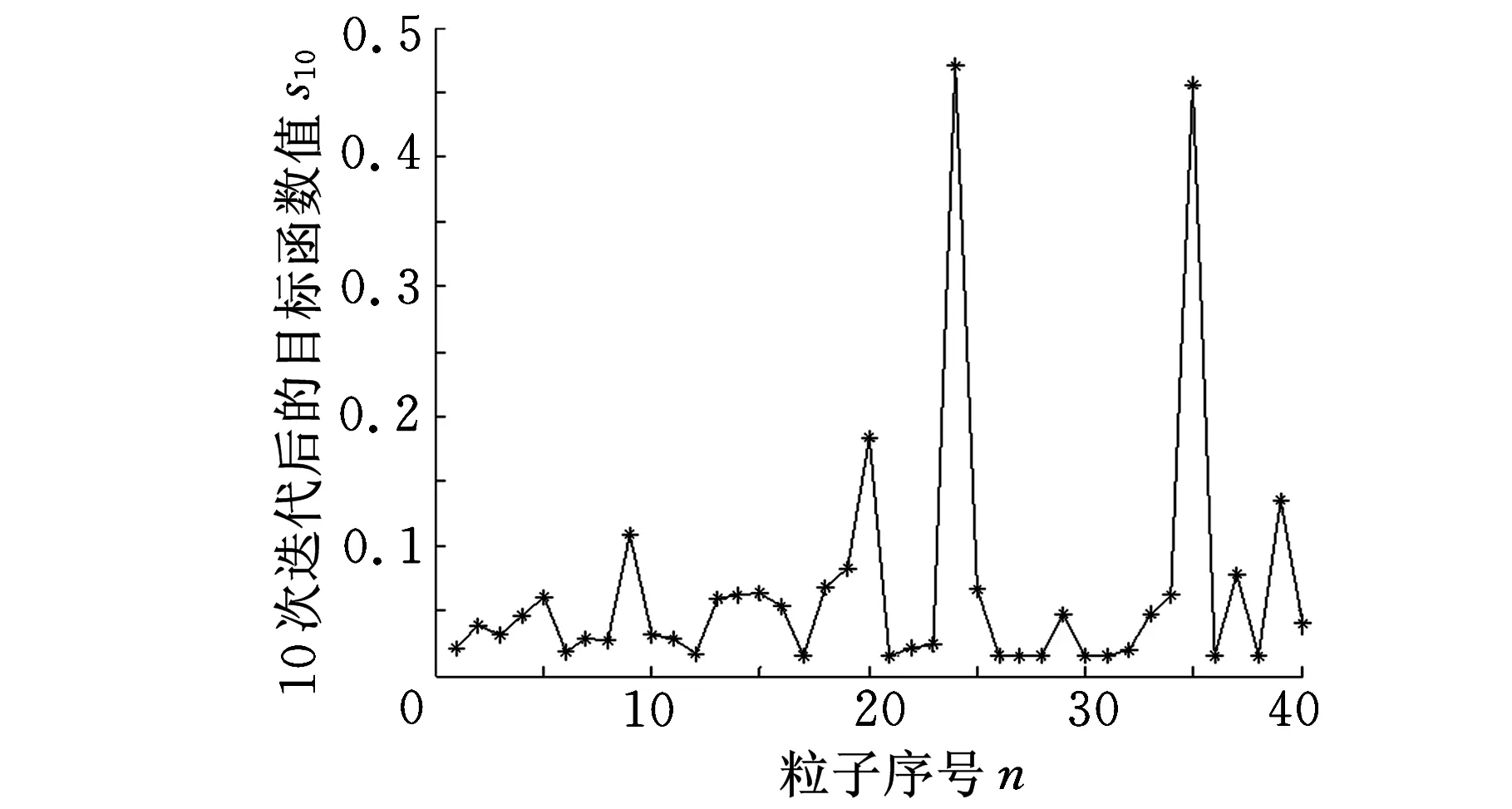
图8　迭代10次各个粒子的目标函数值

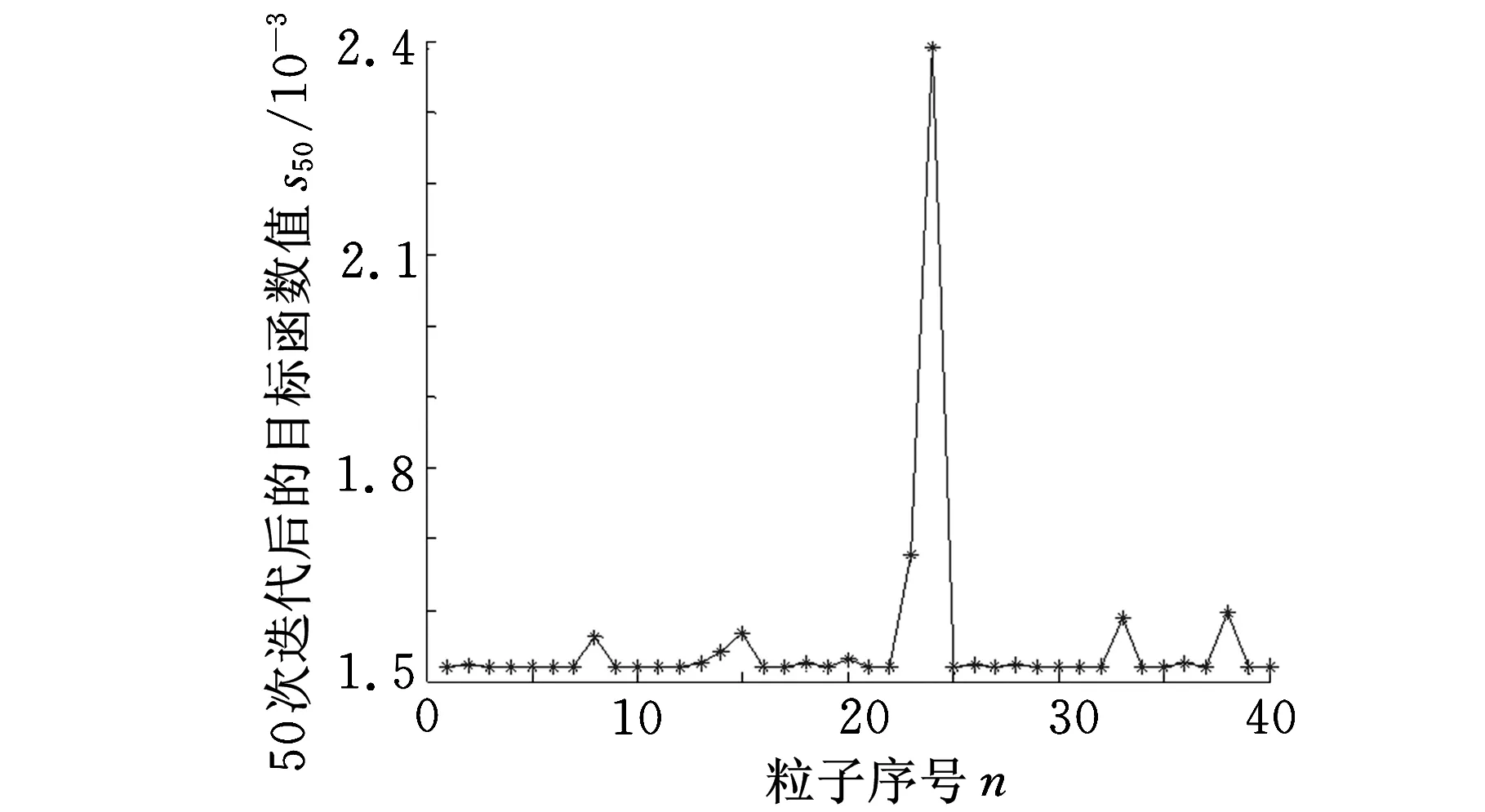
图9　迭代50次各个粒子的目标函数值

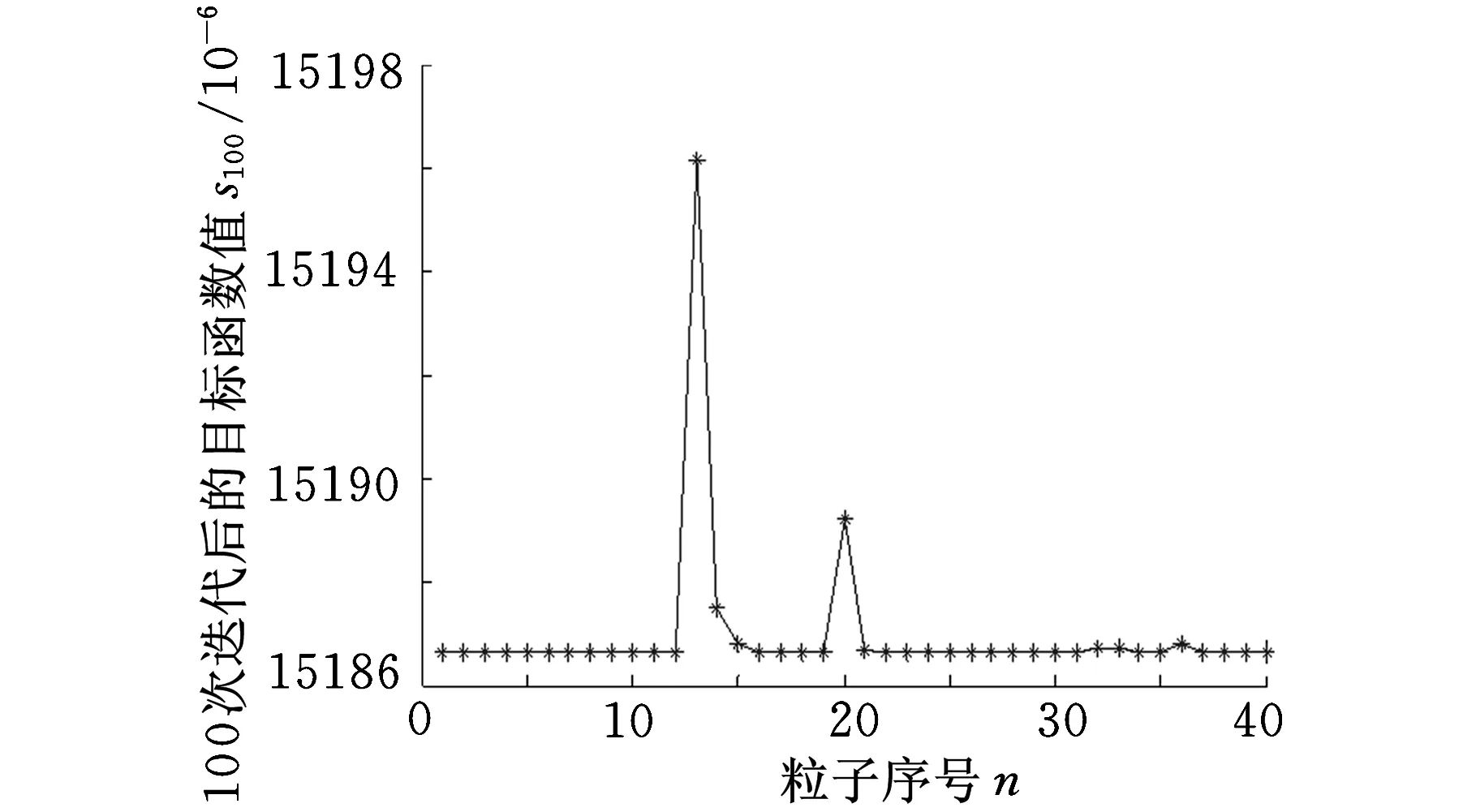
图10　迭代100次各个粒子的目标函数值

将算法得到的最优解按照实际情况进行圆整后得到R1=0.75 mm,D1=2.4 mm,L1=4 mm。基于该尺寸,再利用Fluent进行仿真计算,对其进行验证。图11是经过仿真计算所得到的阀口开度-流量特性曲线与需满足的阀口开度-流量对比图。

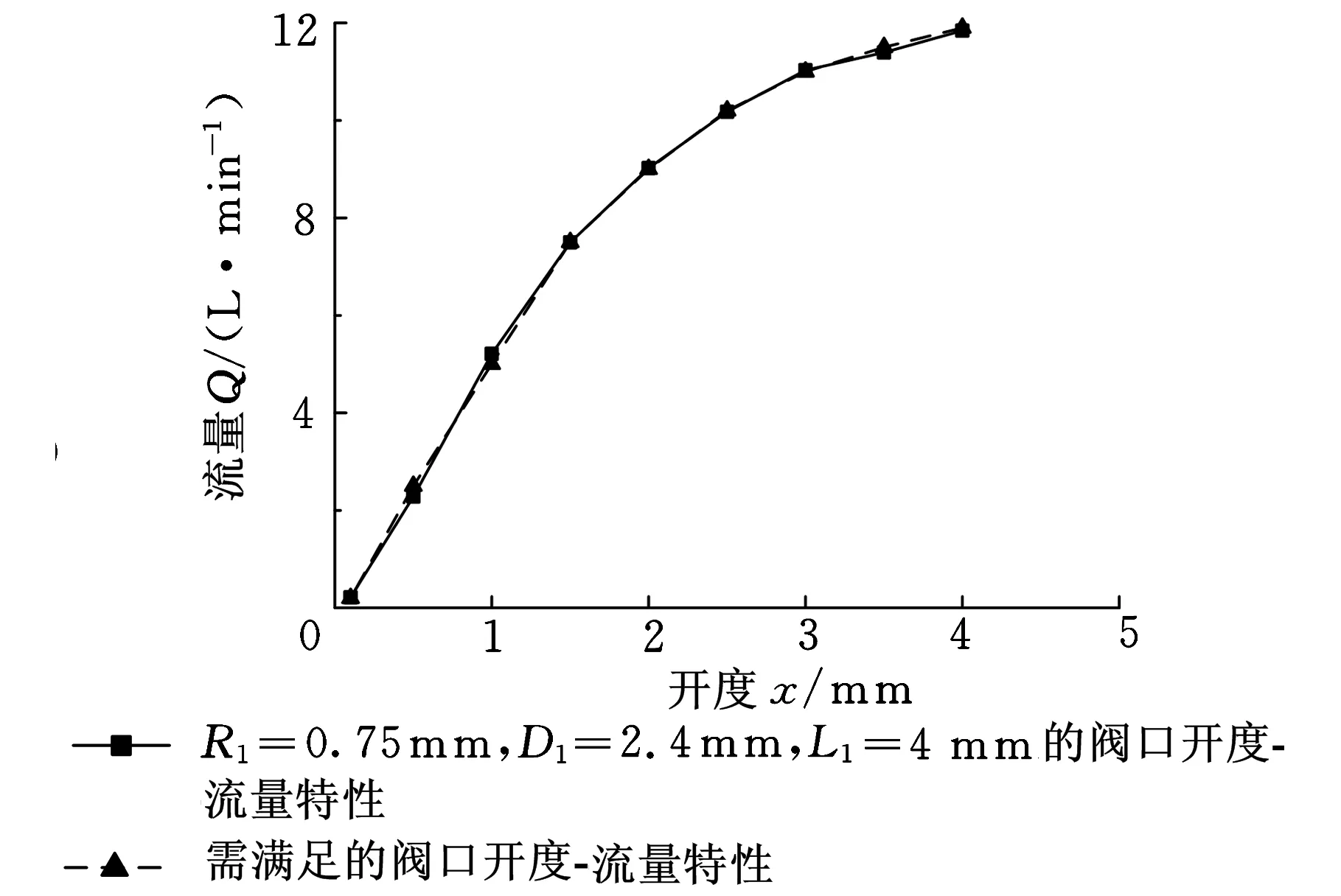
图11　需满足的阀口开度-流量特性与优化尺寸下的阀口开度-流量特性

从图11可以看出,具有运用粒子群算法优化出尺寸的节流槽的阀口开度-流量特性与需满足的阀口开度-流量特性基本一致,因此基于离子群算法的优化方法具有优化效果好、优化精度高的特点。同时,由图7～图10可以看到，初始种群中的粒子散乱地分布在较大的区域内，迭代过程中，粒子个体都在向最优解靠近，迭代到50次时，粒子群体基本集中在最优解附近，迭代到100次时，粒子群基本集中在最优解。

4　结语

随着阀口开度的增加,单U形节流槽的流量梯度逐渐减小,斜U形节流槽的流量梯度基本不变,V节流槽的流量梯度逐渐增大。因此当液压执行机构需要这3种基本节流槽的某一种时,根据其需要的阀口开度-流量特性即可判断节流槽的形状。

当所需满足的阀口开度-流量特性符合3种基本节流槽中某一节流槽的开度-流量特性时,先确定节流槽形状,再依据流量特性数据和该形状下节流槽的仿真数据,运用优化算法便可求得节流槽尺寸参数。

基于粒子群优化算法的滑阀节流槽优化算法,求解结果与所需结果一致,优化效果好。

基于以上的研究结果，后期将结合生产单位的实际需求，开展节流槽口的优化设计工作，并通过具体应用，不断改进和完善优化算法。

[1]冀宏,傅新,杨华勇.几种典型液压阀口过流面积分析及计算[J].机床与液压,2003(5):14-16.

Ji Hong,Fu Xin,Yang Huayong.Analysis and Calculation Typical Shape Orifice Areas in Hydraulic Valves[J].Machine Tool & Hydraulics,2003(5):14-16.

[2]冀宏,王东升,刘小平,等.滑阀节流槽阀口的流量控制特性[J].农业机械学报,2009,40(1):198-202.

Ji Hong,Wang Dongsheng,Liu Xiaoping,et al.Flow Control Characteristic of the Orifice in Spool Valve with Notches[J].Transactions of the Chinese Society of Agricultural Machinery,2009,40(1):198-202.

[3]叶仪,殷晨波,刘辉,等.节流槽阀口静态流动特性研究[J].农业机械学报,2014,45(6):308-316.

Ye Yi,Yin Chenbo,Liu Hui,et al.Study on Stationary Flow Characteristics of Notches with Throttling Grooves[J].Transactions of the Chinese Society of Agricultural Machinery,2014,45(6):308-316.

[4]周会.液压滑阀阀口的特性研究[D].成都:西南交通大学,2009.

[5]王晓娟.小型液压挖掘机多路阀阀芯节流槽研究及应用[D].成都:西南交通大学,2010.

[6]Amirante R,Moscatelli P G,Catalano L A.Evaluation of the Flow Forces on a Direct(Single Stage) Proportional Valve by Means of a Computational Fluid Dynamic Analysis[J].Energy Conversion and Management,2007,48(3):942-953.

[7]Amirante R,Del Vescove G,Lippolis A.Flow Forces Analysis of an Open Center Hydraulic Directional Control Valve Sliding Spool[J].Energy Conversion and Management,2006,47(1):114-131.

[8]彭伊伊.基于粒子群算法的配电网恢复重构的研究[D].武汉:华中科技大学,2012.

[9]汤可宗.遗传算法与粒子群优化算法的改进与应用研究[D].南京:南京理工大学,2011.

(编辑张洋)

Optimization Design of Notches in Spool Valve Based on PSO Algorithm

Li Weijia1Lan Qiuhua1Peng Yong2Yi Disheng2

1.Huazhong University of Science and Technology,Wuhan,430074 2.Sany Car Hoisting Machinery Co., Ltd.,Changsha,410000

Optimization design of three basic notches including single-U-shaped,ramp-U-shaped and V-shaped was investigated thoroughly.Fluent,the flow field simulation software,was used to calculate the flow of different notches at different displacements in the constant pressure,and the experiments were done to make sure the reliability of the simulation results from Fluent by the comparison of simulation results with experimental ones.And it is found that the flow gradient of single-U-shaped notch decreases with its displacement increases,the flow gradient of V-shaped notch basically unchanges with its displacement increases,and the flow gradient of single-U-shaped notch increases with its displacement increases.Using the PSO algorithm and combining some notch simulation calculation results,the optimal sizes of notches were obtained,which could meet the required displacement flow characteristics good effectiveness.And one case that the required displacement flow characteristics verified that the optimization algorithm has high precision,compared with simulation results from optimal sizes.

notch;optimization design;flow characteristics;particle swarm optimization(PSO) algorithm

2014-05-13

国家科技支撑计划项目(2012BAF022B01)

TH137.52DOI：10.3969/j.issn.1004-132X.2015.08.001

李维嘉,男,1964年生。华中科技大学船舶与海洋工程学院教授、博士研究生导师。主要研究领域为液压系统控制、船舶机电仿真。获省部级科技进步二等奖2项、三等奖4项。兰秋华,女,1989年生。华中科技大学船舶与海洋工程学院硕士研究生。彭勇,男,1984年生。三一汽车起重机械有限公司工程师。易迪升,男,1966年生。三一汽车起重机械有限公司高级工程师。