基于应变梯度塑性理论的微塑性成形力学性能

郭幼丹　程晓农

1.集美大学，厦门，361021　　2.江苏大学，镇江，212013

基于应变梯度塑性理论的微塑性成形力学性能

郭幼丹1程晓农2

1.集美大学，厦门，3610212.江苏大学，镇江，212013

T2紫铜；力学性能；应变梯度理论；微塑性成形

0　引言

随着微机电系统(MEMS)等技术的蓬勃兴起和快速发展，微金属构件的需求日益增多，形成巨大的市场需求。但是，当微结构尺寸达到微米量级时，材料微塑性成形时通常表现出两种与尺度有关的效应[1-2]：一是晶粒尺度对材料性能影响的晶粒尺度效应(grain size effects)；二是特征尺度(长度、宽度、厚度、直径等描述材料外形的尺度参数)效应或试样尺度效应(feature size effects or specimen size effects)。这两种尺度效应都将导致微金属构件在微塑性成形中表现出显著的尺度依赖行为，而且随着特征尺寸的减小，呈现出一种“越小越强”的独特现象[3]。早在20世纪初，Cosserat等[4]提出了微极非线性弹性理论，但该理论在纯拉压荷载下作为正则化机制而引入的对偶应力将不起作用。20世纪80年代后期，随着微金属构件的应用，金属材料微塑性成形中新的科学问题的出现重新引起学者的广泛重视和研究。如Mindlin[5]将弹性体的应变能密度视为应变和它的第一、第二阶导数的函数，给出了一种更常用的仅包含应变和其一阶导数的简化理论；Fleek等[6]在细铜丝扭转实验中观测到微尺度下应变梯度的硬化；Stolken等[7]通过试验发现镍的量纲一弯曲硬化随着薄片厚度的减小而明显增大；Aifantis等[8-9]建立了应变梯度塑性理论，并解释了不常见微结构标准尺寸试件、普通微结构小尺寸试件在扭转和弯曲中的微尺度效应；Lam等[10]研究了微悬臂梁的弯曲问题，发现微梁的量纲一刚度与梁厚二次方成反比关系。国内的一些学者也开展了相关的研究，如黄克智等[11]综合了偶应力和应变梯度塑性理论并对其进行了介绍；李河宗等[12]对不同厚度及粗细两种晶粒尺寸的黄铜箔试样进行了单向拉伸和微弯曲实验研究；聂志峰等[13]进行了应变梯度弹性理论下微构件尺寸效应的数值研究；周丽等[14]运用应变梯度塑性理论模拟颗粒增强铝合金强度及延伸率的尺寸效应。这些研究主要从微尺度下的应变梯度塑性理论、一些特殊微结构件的微尺度效应等方面进行研究，对进一步研究微尺度效应具有很好的借鉴意义。T2紫铜电极无方向性，导电性能极佳，加工性、延展性、防蚀性及耐候性良好，在电子行业应用极为广泛，但鲜有研究人员对T2紫铜微成形中微尺度效应开展研究。本文主要研究T2紫铜的单向拉伸、硬度和微弯曲性能特点，并对试验中表现出的尺寸效应现象进行分析与讨论。

1　试验设计

1.1试验材料

试验材料为T2紫铜，厚度分别为: 30、60、90、120、150 μm，其化学成分见表1，力学性能见表2。

表1　T2紫铜主要成分　%

表2　T2紫铜力学性能

材料的退火处理方式如下：加热温度分别为400 ℃和620 ℃，保温时间为1.2 h，冷却速度为0.5 ℃/s。通过退火处理，可消除材料轧制织构对试验的影响，细化晶粒，获得试验所需的粗晶和细晶晶粒尺寸的试样。晶粒大小采用 ASTM E112-96(2004)平均晶粒度测定方法(GB/T 6394-2002)获得。

1.2试验方法与设备

1.2.1单向拉伸试验

单轴微拉伸试验系统设计如下：在美国伊利诺斯州立大学Saif 教授设计的薄膜材料力学性能测试系统基础上，根据材料和测试要求，设计适用于本课题要求的单轴微拉伸系统，整个微拉伸测量系统主要由三维可调平台、力传感器、位移传感器、力传感器、驱动装置、图像采集、机械框架和夹具等部分组成。单向微拉伸试验微试件的几何尺寸如图1所示。试件在激光切割机上切出。拉伸试验时，由双视场显微镜与CCD数码视频相机对拉伸过程进行全程的跟踪拍照记录，检测试样拉伸时标距长度的变化情况，然后通过计算机处理得到应变数据，绘制材料单向拉伸应力应变曲线。

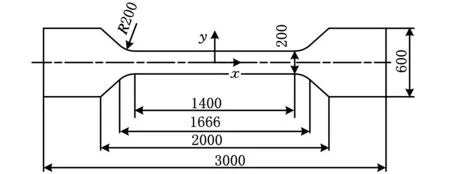
图1　微试件的几何结构(μm)

1.2.2微弯曲试验

微弯曲试验如图2所示。微弯曲试验相关参数设定如下：h为板材厚度，C为弯曲凸凹模之间的间隙(弯曲间隙)，Rp为凸模圆角半径，Rd为弯曲凹模圆角半径，u为凸模运动速度。试验时由CCD数码视频相机对微弯曲过程进行全程的跟踪拍照记录，得到微弯曲过程关键位置弯曲情况，弯曲角度通过冲头行程控制；在计算机上采用边缘检测算法即时对拍摄的图片进行图像处理，得到相应的弯曲及回弹后的角度，通过数据处理得到弯曲回弹角。为了保证试验的普遍性，重复上述试验8次，然后取回弹角的平均值。

图2　微弯曲试验示意图

1.2.3微硬度试验

图3为微硬度试验示意图。在微硬度实验机上检测弯曲圆弧变形区域侧面硬度的变化情况，获得压痕点的硬度，以研究变形区的硬度变化情况。图中的楔形压头角度β=140.6°，20 s内加载100 mN，保压时间为5 s，h为板材厚度，δ为压痕深度，Ac为真实接触长度，P为压头所受的支反力之和，即压痕力。微压痕真实硬度Hc定义为平均接触压力，即Hc=P/Ac。

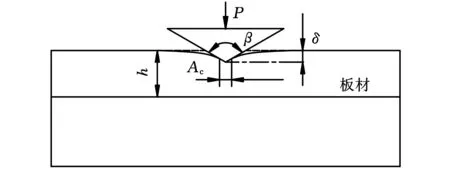
图3　微硬度试验示意图

2　结果与讨论

2.1特征尺度对拉伸的影响

(1)

式中，εe为等效Cauchy应变，反映了统计存储位错对材料硬化的影响；xe为等效曲率，反映了几何必须位错对材料硬化的影响。

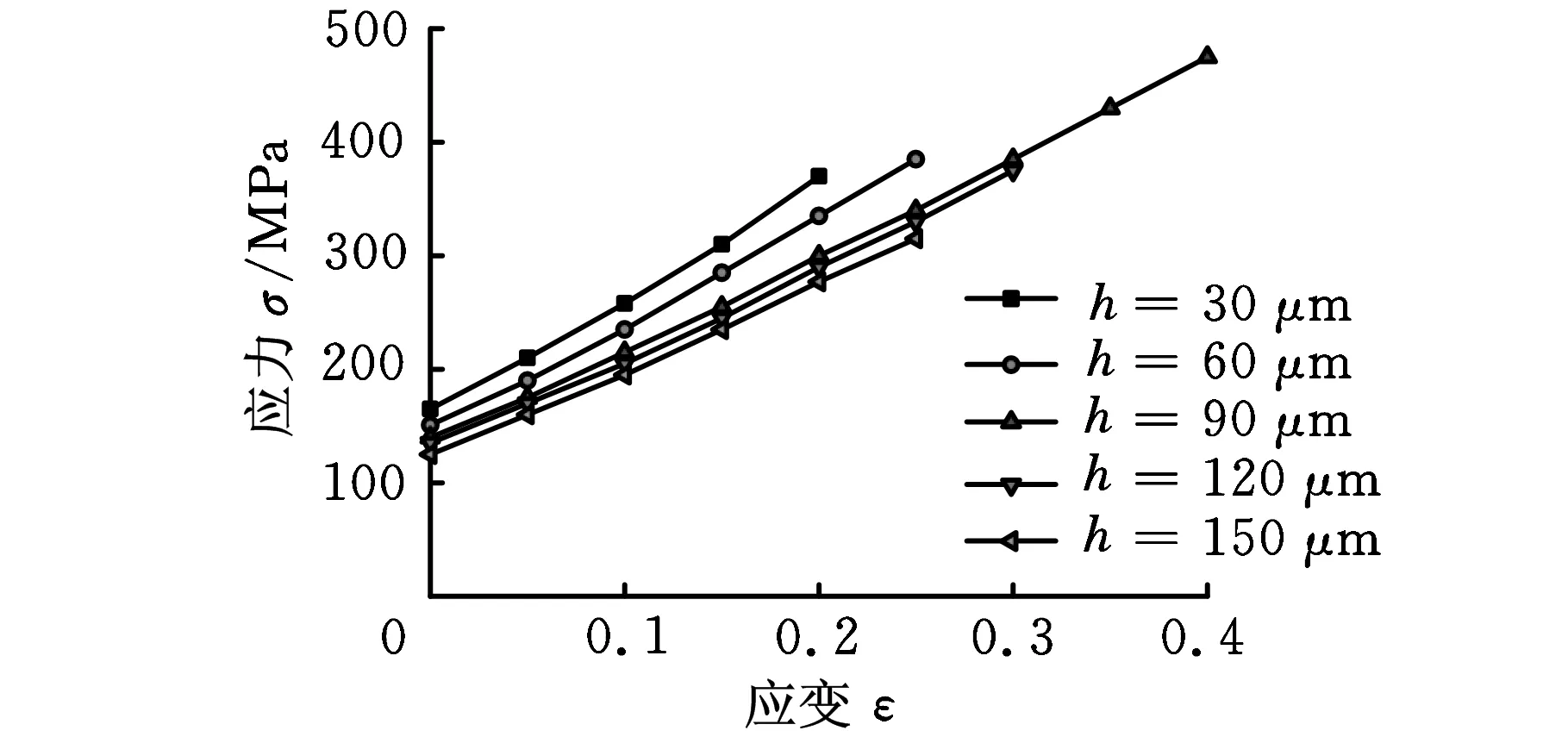
(a)不同厚度板材应力-应变曲线(晶粒平均尺寸为20 μm)

(b)细晶与粗晶应力-应变曲线(板材厚度150 μm)图4　微塑性变形应力-应变曲线

2.2特征尺度对硬度的影响

图5所示为板厚为150 μm、晶粒平均尺寸为50 μm时特征尺寸效应对硬度的影响。图5a为不同压入深度与压痕力关系曲线。从图中可以看出，在相同的压入深度下，压痕力随着内禀尺度增大而增大。图5b为不同压入深度与压痕硬度关系曲线。从图中可以看出，不同的压入深度，压痕硬度是不同的，当压痕深度(δ)与板材厚度(h)比值小于等于0.2时，压入深度增大，压痕硬度变小，呈现“越大越软”现象；当压痕深度δ与板材厚度h的比值大于0.2时，压入深度增大，压痕硬度增大，呈现“越大越硬”现象。事实上，塑性硬化不仅同应变和旋转梯度有关, 还同拉伸梯度相关, 其等效塑性应变满足以下关系[16]：

(2)

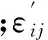
(a)压入深度与压痕力关系曲线

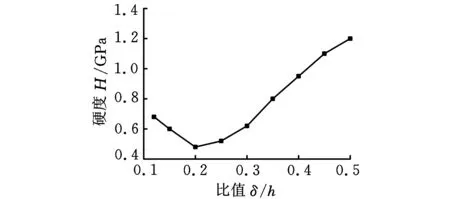
(b)压入深度与压痕硬度关系曲线图5　特征尺度效应对硬度的影响(晶粒平均尺寸为50 μm)

与宏观构件相比，微构件在材料表面的晶粒个数占总晶粒个数的百分比很高(如细晶)，材料表面的晶粒受周围晶粒的约束作用小，因此，当压入深度较小时，晶粒容易产生滑移，从而使流动应力减小，强度降低，产生“越大越软”的尺度效应现象。随着压入深度的增大，板材厚度方向的晶粒已减少至1～2个晶粒, 晶粒位向一致的可能性增大，产生附加的几何必须位错，硬化作用增强，产生“越大越硬”的尺度效应现象。这样的硬度变化规律也被Saha等[17]和Liu等[18]通过试验和数据预测所证实。

2.3特征尺度对回弹的影响

图6为不同厚度下回弹角的试验值与理论预测对比图，其中s0为传统理论计算值，s1为应变梯度理论计算值，s2为试验结果值。从图中可以看出，试样实测的回弹角基本上随板料厚度的减小而增大，特别是当材料厚度小于一定值(0.06mm)时，回弹角随板料厚度的变化更为剧烈，这种变化来自于微塑性成形中材料的应变梯度硬化效应，说明在微塑性成形中不仅存在微尺度效应现象，而且应变梯度在微弯曲过程中起着相当重要的硬化作用。

图6　不同厚度板材弯曲90°时的回弹角

s0曲线为应用传统弯曲理论预测得到的弯曲回弹角变化曲线，可以看出，曲线基本呈水平状，除随屈服强度的变化有微小的波动外，回弹角基本不随材料厚度的变化而变化，这与试验结果存在明显差异，说明在微塑性成形中传统弯曲理论并不适用。s1曲线为应用应变梯度理论预测得到的弯曲回弹角变化曲线，此时，回弹角随材料厚度变化曲线与试验结果较接近，当材料厚度小于一定值(0.06 mm)后，两者变化基本一致，说明微塑性成形中应用应变梯度塑性理论能够较为准确地反映材料弯曲过程中出现的应变梯度硬化效应，较为准确地预测材料弯曲回弹现象，得到更为合理的结果。

3　结论

(2)当T2紫铜的压痕深度δ与板材厚度h的比值小于等于0.2时，随着压入深度增大，压痕硬度变小，呈现“越大越软”现象；当比值小于0.2时，随着压入深度增大，压痕硬度增大，呈现“越大越硬”现象。

(3)T2紫铜微弯曲时，回弹角随板料厚度的减小而增大，当板料厚度小于一定值(0.06 mm)时，材料的应变梯度硬化效应使得回弹角随板料厚度的变化更为剧烈，与应用应变梯度理论预测得到的弯曲回弹角变化曲线基本一致。

[1]Geiger M,Mebner A,Engel U.Production of Microparts-size Effects in Bulk Metal Forming.Similarity Theory[J].Production Engineering,1997,4(1):55-58[2]Koeanda A,Pres T.The Effeet of Miniatunzation on the Final Geometry of the Bent Produet[C]//the English Iniemational Conference on Metal Forming.Rotterdam,2000:68-72.

[3]Hutehinson J W.Plastieity at the Micro-sceale.Intemational[J].Joumal of Solids and Structures,2000,37(1/2):225-238.

[4]Cosserat E,Cosserat F.Theorie Des Corps Deformables[J]. Hermann & Fils, 1909(3):26-29.

[5]Mindlin R D.Second Gradient Plasticity[J].Adv. App. Mech.,1997,33:295-361.

[6]Fleck N A,Muller G M,Ashby M F,et al. Strain Gradient Plasticity:Theory and Experiment[J]. Acta Metall. Mater.,1994,42:475-487.

[7]Stolken J S,Evans A G.A Microbend Test Method for Measuring the Plasticity Length Scale[J]. Aeta Metall. Mater.,1998,46:5109-5115.

[8]Aifantis E C.On the Microstructural Origin of Certain Inelastic Models[J].Mater.Engng.Technol.,1984,106:326-330.

[9]Aifantis E C.Strain Gradient Interpretation of Size Effects[J].International Journal of Fracture,1999,95(1/4):299-314.

[10]Lam D C C,Yang F,Chong A C M,et al.Experiments and Theory in Strain Gradient Elasticity[J].Mech. Phys. Solids,2003,51:1477-1508.

[11]黄克智，邱信明，姜汉卿.应变梯度理论的新进展(一)偶应力理论和SG理论[J].机械强度，1999，21(2)：81-87.

Huang Kezhi,Qiu Xinming,Jiang Hanqing. Recent Advances in Strain Gradient Plasticity-Ⅰ——Couple Stress Theory and SG Theory[J].Journal of Mechanical Strangth,1999,21(2):81-87.

[12]李河宗，董湘怀，王倩,等. CuZn37黄铜板料微塑性成形中的尺寸效应研究[J].材料科学与工艺，2011，19(4)：15-19.Li Hezong,Dong Xianghuai,Wang Qian. Size Effects of CuZn37 Brass Foil in Microforming[J]. Materials Science and Technology,2011,19(4):15-19.[13]聂志峰,周慎杰,韩汝军,等.应变梯度弹性理论下微构件尺寸效应的数值研究[J].工程力学，2012，29(6)：38-46.

Nie Zhifeng,Zhou Shenjie,Han Rujun,et al. Numerical Study on Effects of the Microstructures Based on Strain Gradient Elasticity[J]. Engineering Mechanics,2012,29(6):38-46.

[14]周丽，李守新，黄树涛.运用应变梯度塑性理论模拟颗粒增强铝合金强度及延伸率的尺寸效应[J].功能材料，2008，39(12)：2101-2105.

Zhou Li,Li Shouxin, Huang Shutao. Simulation of Size Effect on Strength and Elongation of Al Alloy Wity Rarticles Reinforcement Using Strain Gradient Plasticity Concept[J].Journal of Functional Materials,2008,12(39):2101-2105.

[15]Fleck N A, Hutchinson J W. A Phenomenological Theory for Strain Gradient Affects in Plasticity[J]. Journal of the Mechanics and Physics of Solids, 1993, 41: 1825-1857.

[16]Fleck N A, Hutchinson J W. Strain Gradient Plasticity[J]. Advanced Applied Mechanics, 1997, 33: 295-361.

[17]Saha R, Xue Z, Huang Y, et al. Indentation of a Soft Metal Film on a Hard Substrate: Straingradient Hardening Effects[J].Mech. Phys. Solids, 2001, 49:1997-2014.

[18]Liu Z L, Zhuang Z, Liu X M, et al. A Dislocation-dynamics Based Higher-order Crystalplasticity Model and Applications on Confined Thin-film Plasticity[J]. Int. J. Plast., 2011,27:201-216.

(编辑王艳丽)

Mechanical Properties of Micro Plastic Forming Based on Strain Gradient Theory

Guo Youdan1Cheng Xiaonong2

1.Jimei University,Xiamen,Fujian,361021 2.Jiangsu University,Zhenjiang,Jiangsu,212013

T2 red copper; mechanical property; strain gradient theory; micro plastic forming

2014-01-11

国家自然科学基金资助项目(50772044)；福建省自然科学基金资助项目(2014J01200)；福建省教育厅科技计划资助项目(JA12197)

TG301< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.05.021

郭幼丹，男，1960年生。集美大学机械与能源工程学院副教授。主要研究方向为精密成形技术。发表论文50余篇。程晓农，男，1958年生。江苏大学材料科学与工程学院教授、博士研究生导师。