用GAAA优化多阶段装配过程中的夹具布局

谢伟松　邓　铮　丁伯慧

1.天津大学，天津，3000722.天津大学机构理论与装备设计教育部重点实验室，天津，300072

用GAAA优化多阶段装配过程中的夹具布局

谢伟松1邓铮1丁伯慧2

1.天津大学，天津，3000722.天津大学机构理论与装备设计教育部重点实验室，天津，300072

改进了遗传算法与蚁群算法的融合(GAAA)算法，利用它来解决多阶段装配过程中二维刚性零件的夹具布局优化问题，合理选择定位销的位置使得灵敏度指标最小化。通过改变遗传算法的变异算子，变异长度以及交叉、变异在蚁群算法中发生的位置，提高了GAAA的稳定性和收敛性。以汽车侧边装配为例验证了改进算法的有效性，结果表明改进后的GAAA比基本的GAAA和蚁群算法求得的结果要好，且收敛速度更快，稳定性更好。

多阶段装配过程；状态空间模型；夹具布局优化；遗传算法与蚁群算法的融合

0　引言

夹具设计在很大程度上影响了装配过程中的产品尺寸变化，对于一种新产品的过程设计，它是最重要的设计任务之一。在汽车工业中，装配过程是一种典型的多阶段板类装配过程，其中，夹具用来定义零件和子配件的位置，并且为其提供物理支撑。夹具设计极大地影响了多阶段装配过程中最终产品尺寸的准确性，从而相对于外部变化，夹具布局设计合理可以减小过程灵敏度。一个最优的夹具布局能够改善一个夹具系统的鲁棒性，克服环境噪声，减少产品变化和降低制造成本。

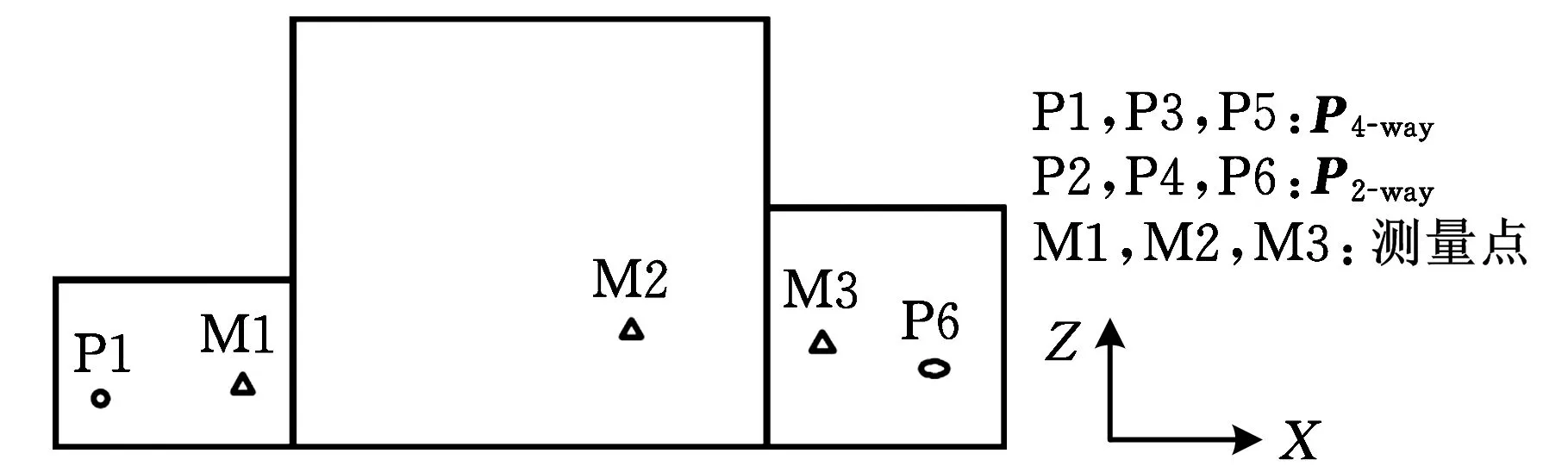
多阶段板类装配过程中的夹具通常用n-2-1布局，包括两个定位销和n个净接触(net contact，NC)块，记为{P4way,P2way,NCi,i=1,2,…,n}。对于二维模型，我们只考虑定位销引起的变化，所以布局可写为{P4-way,P2-way}。

在夹具布局优化问题中，子配件重新定位引起的变化在各阶段间的联系，使得夹具分布问题或者主要定位点(PLPs)分布简化问题在多阶段过程中变得更困难。Kim等[1]解决了多阶段装配过程中二维刚性零件的此类问题，将改进后的基本交换算法作为优化方法来确定PLP的分布。Izquierdo等[2]在产品系列的夹具布局设计中延伸了Kim等[1]的工作，提出了一种新方法：在一种产品系列的多阶段装配中，通过定位元件的最优分布来获得夹具布局设计的鲁棒性。Huang等[3]用序列空间填充方法来解决多阶段装配系统中夹具布局的鲁棒设计问题，并将序列子空间搜索方法和直接的空间填充以及遗传算法(GA)进行了比较。在单一阶段的夹具布局优化问题中，文献[4-6]分别采用ANN(artificialneuralnetworks)和GA解决了鲁棒夹具布局设计和夹紧力优化的问题。文献[7-8]分别采用基于离散型和连续型的蚁群算法(ACA)对夹具布局进行优化，使得工件的弹性变形最小。通过上述的研究工作可以发现：GA和ACA在夹具布局优化问题中具有广泛的应用性，但是文献[7-8]采用ACA只是对单一阶段单一工件的夹具布局进行优化，并且ACA的初期信息素匮乏，求解速度慢。

本文对基于连续型方法的ACA与GA的融合算法(geneticalgorithm-antcolonyalgorithm,GAAA)进行了改进，用GA克服了ACA初期信息素匮乏的问题，采用改进的GAAA来解决二维刚性零件在多阶段装配过程中夹具布局优化问题，并将改进的GAAA与基本的GAAA以及ACA求得的结果进行比较。将E-optimality标准的最小化作为目标函数，合理选择定位销或者PLPs的位置使得灵敏度指标最小化。

1　变化传播模型与优化方案

1.1变化传播模型

xk=Ak-1xk-1+Bkuk+wk

(1)

yk=Ckuk+vk

(2)

其中，xk为阶段k(k=1,2,…,N)的变化(零件的偏移和旋转)，xk∈Rn；uk为夹具偏差,uk∈Rp；wk为其他未建模的偏差，wk∈Rn；矩阵Ak-1表示两个相连阶段夹具布局的关系，决定了阶段k子配件重新定位的位置；矩阵Bk表示阶段k的夹具布局,Bk∈Rn×p；yk表示阶段k的测量或输出，依赖于测量点的位置,yk∈Rm；矩阵Ck表示零件变化与测量点之间的关系,Ck∈Rm×n；vk为噪声,vk∈Rm。上述方程中矩阵Ak、Bk、Ck的具体表示参见文献[1,13]。

由于状态空间模型具有线性性质，所以得到线性输入-输出状态空间模型：

(3)

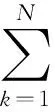
1.2灵敏度指标

假设在装配过程中变化的主要来源是夹具(例wk≈0,vN≈0,x0≈0)，则夹具引起的产品变化可写为

在夹具布局设计中有三种优化标准:

D-optimality:min det(DTD)

A-optimality:min tr(DTD)

E-optimality:minλmax(DTD)

三种标准的具体描述可见文献[1]，本文采用E-optimality标准。Kim等[1]将灵敏度指标定义为

在分析9个注水系统中，果7注水系统存在回流，回流量为5 m3/h，如果通过及时调整注水泵的运行频率，使注水量与注水泵排量吻合，避免出现打回流现象。系统的注水单耗为14.33 kWh/m3，此运行状况按照运行2个月计算，则避免回流可节约电量为10.32×104kW。

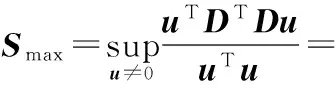
1.3优化方案

Kim等[1]用E-optimality标准得到优化方案：

minφSmax=λmax(DTD)

s.t.G(φ)>0

约束G(φ)是限制产品的主要定位点(PLPs)位置φ的几何约束的集合，它们包括定位元件的可行域以及零件之间的关系。如果产品在XZ平面上定位m个零件，则向量φ包括2m个PLPs的位置。PLPs的位置主要是2个定位销的位置，产品的PLPs位置表示为φ=(P1,P2,…,P2m)，其中,Pk=(xk,zk),k=1,2,…,2m，所以φ还可写为φ=((x1,z1),(x2,z2),…,(x2m,z2m))。

2　优化算法

2.1改进的融合算法

遗传算法与蚁群算法的融合是由丁建立等[14]提出的。本文中，将文献[14]中的GAAA称为基本的GAAA，本文的算法称为改进的GAAA。

随机选取10个夹具布局，将每个夹具布局的目标函数值按其从小到大的顺序排列，第1～6个夹具布局称为上解，第7～10个夹具布局称为下解。用蚁群算法的全局搜索来改变下解的夹具布局(如文献[7-8])，用遗传算法的顺序交叉法和逆转变异法(如文献[14-15])来改变上解的夹具布局，将第1～6个夹具布局的P4-way(或P2-way)的x或y轴坐标值组成一个父串，并采用十进制对其编码。例如P4-way的横坐标可以组成一个父串：

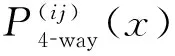
本文针对GAAA作了如下三点改进：

(1)改变遗传算法中的变异算子。基本的GAAA是选择一个处于相连位置的变异序列，这样发生变异的元素会相对集中。改进措施为，随机选取一些不相连的变异位置，将处于这些变异位置的数码取出来组成一个变异序列，将其逆转后再依次放入原来序列的空位置中。

假设最优布局的编码为1，2，3，4，5，6。

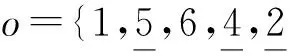
(2)每次选定的变异长度不是一个定值，而是一个随机变化的变异长度。

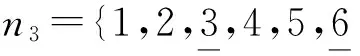
(3)遗传算法的交叉、变异过程嵌在蚁群算法过程中，如图1所示。步骤(8)、(9)、(10)在步骤(7)和(11)之间进行，而不是只在蚁群算法运行前进行。

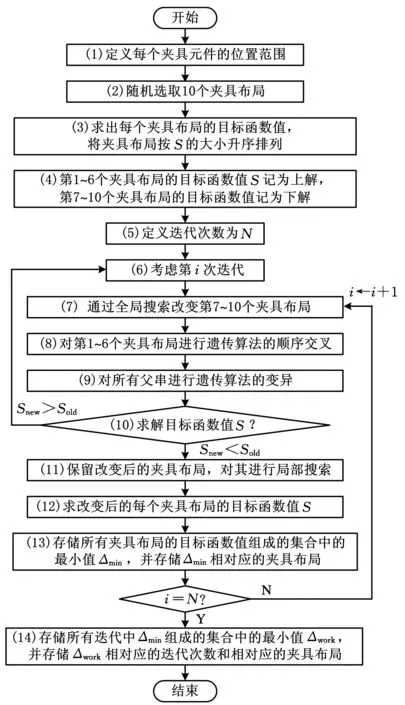
图1　融合算法流程图

2.2收敛过程

用融合算法对每个夹具布局的每个夹具元件进行优化，求出每个夹具布局的最大特征值Smax，存储所有夹具布局M中最大特征值Smax的最小值Δmin以及相对应的夹具布局(图1)。对所有的迭代过程N均重复同样的过程，求出所有Δmin中的最小值Δwork以及最小值对应的夹具布局。如果迭代次数达到设定的最大迭代次数N，并且每次迭代后的元件位置均在夹具元件的位置范围内，或者每一次迭代的结果浮动范围较小，趋于稳定，那么算法收敛。

3　实例分析

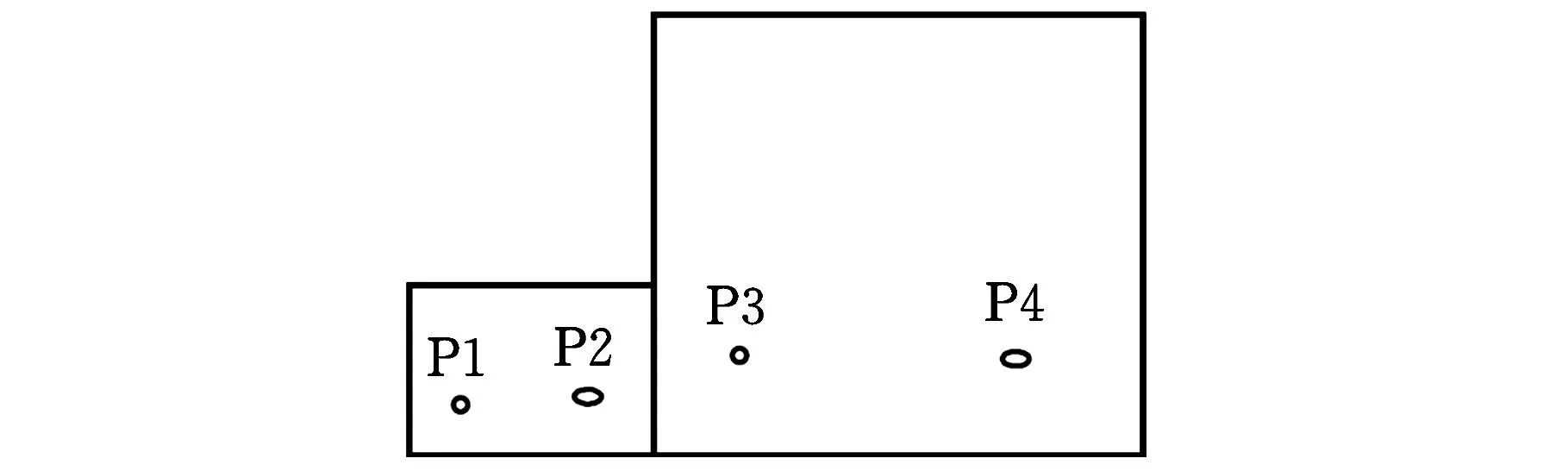
下面以车身侧边装配过程为例验证算法的有效性。这个侧边主要包括车头(fender side)、车身(A-B ring)和车尾(rear quarter)三个部分，如图2a所示。每个零件的形状简化为矩形，这三个部分记为零件1、零件2和零件3，三个零件在坐标中的大小已在图2b中标出。图3给出了装配顺序和基准变换：

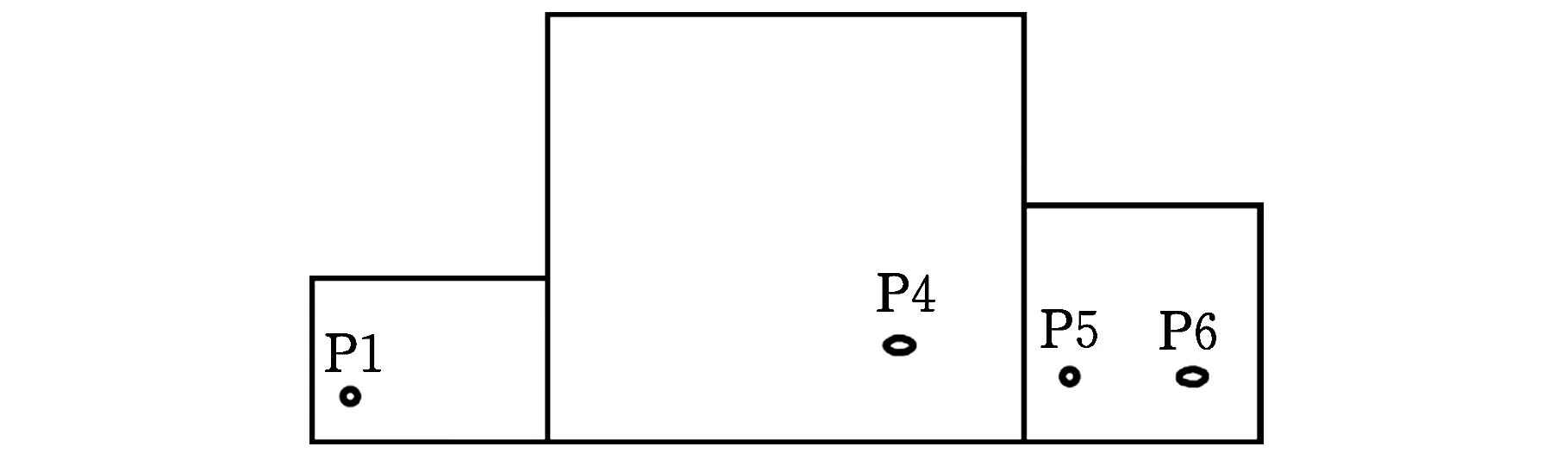
{{P1,P2},{P3,P4}}Ⅰ→

{{P1,P4},{P5,P6}}Ⅱ→{{P1,P6}}Ⅲ

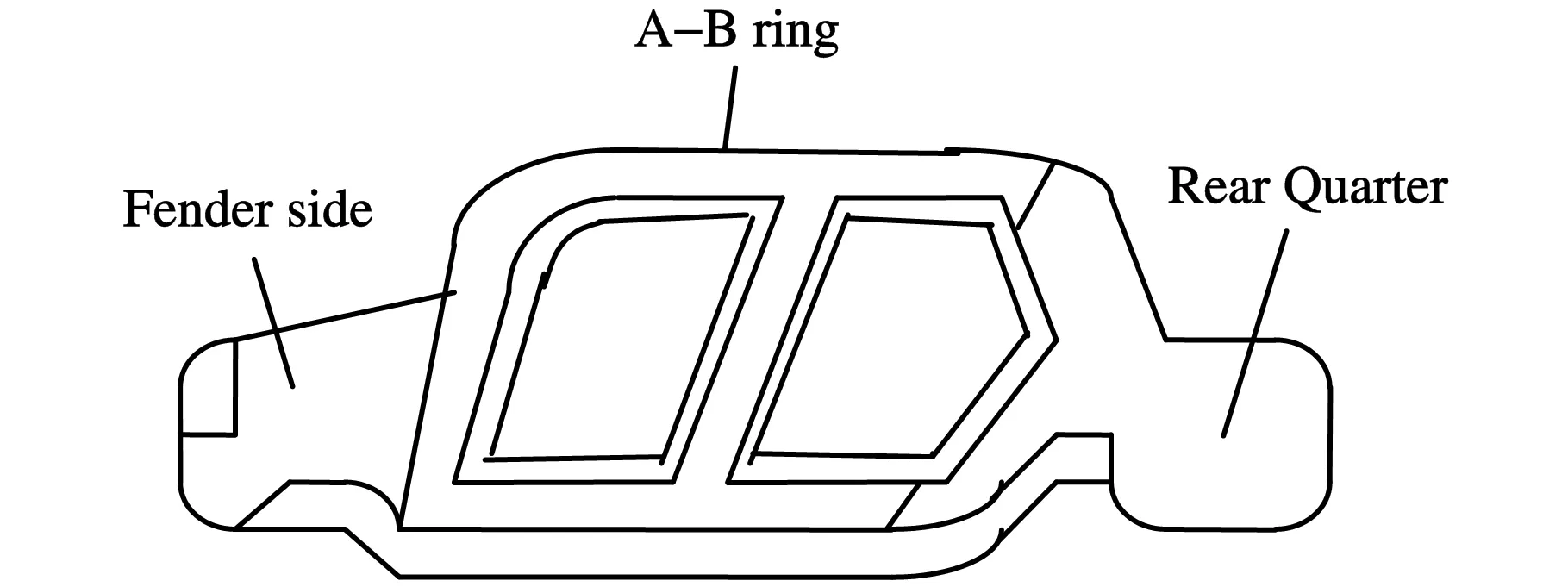
(a)车辆侧边框

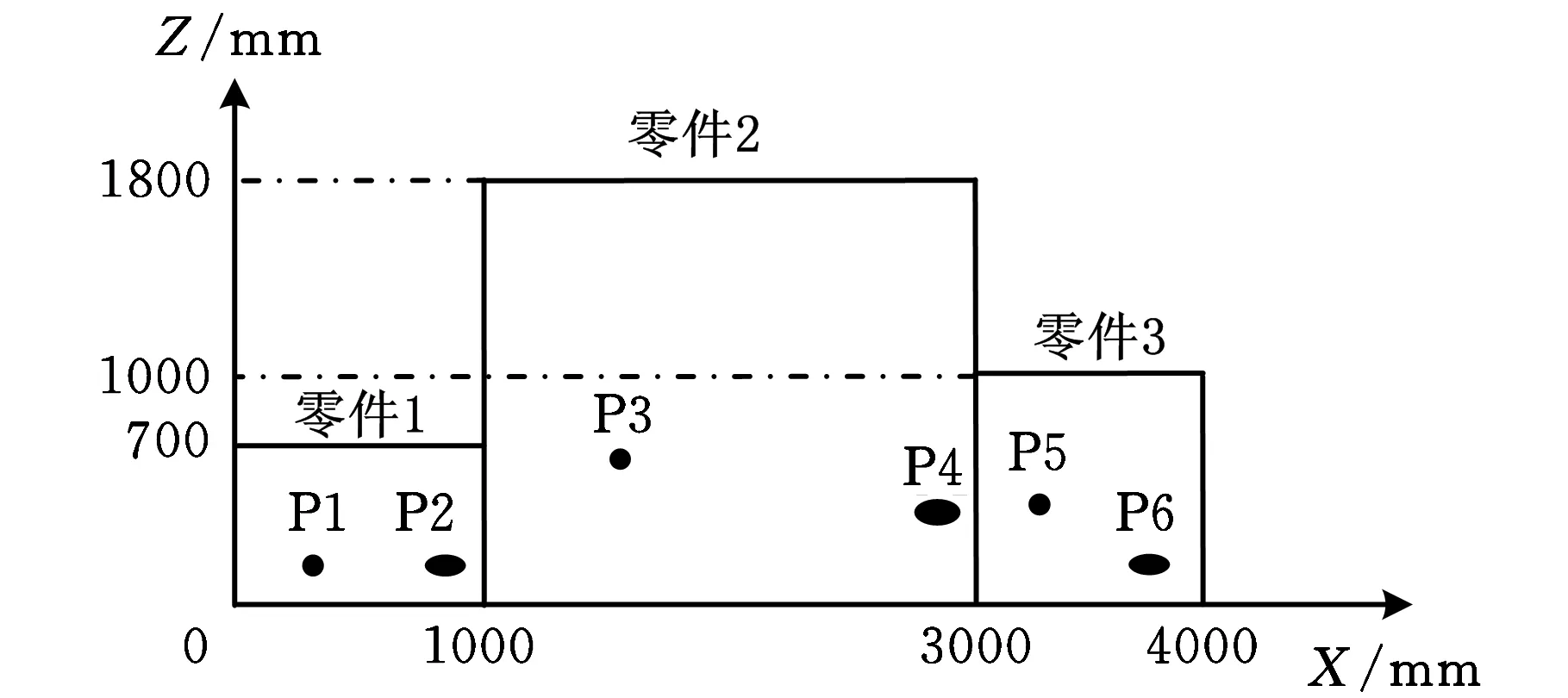
(b)零件大小示意图2　装配的几何参数

(a)阶段1

(b)阶段2

(c)阶段3图3　装配过程

用MATLAB软件求得的结果如下(所有单位为mm)：

图4a、图5a、表1和表2表示在相同参数和相同的初始夹具布局下，蚁群算法和改进的GAAA求得的结果比较。其中，图4a所示为二者的迭代过程，表1所示为二者求得的最优夹具布局。图5a将表1中PLPs的坐标用CAD软件标注在工件上，“+”表示蚁群算法求得的最优夹具布局，“o”表示改进的GAAA求得的最优夹具布局；表2是二者求得的最小目标函数值。从图4a可以看出，在相同参数和相同的初始夹具布局下，改进的GAAA比蚁群算法稳定性更好，收敛速度更快，蚁群算法在大概迭代50次之后趋于稳定，而改进的GAAA在大概迭代40 次之后就趋于稳定，且从表2可以看出，改进的GAAA求得的最小目标函数值2.0071也比蚁群算法求得的结果2.0240要小。

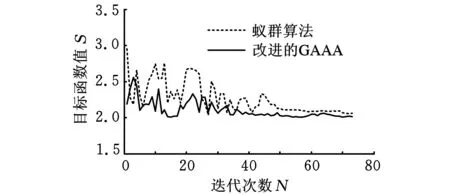
(a)蚁群算法和改进的GAAA的迭代过程

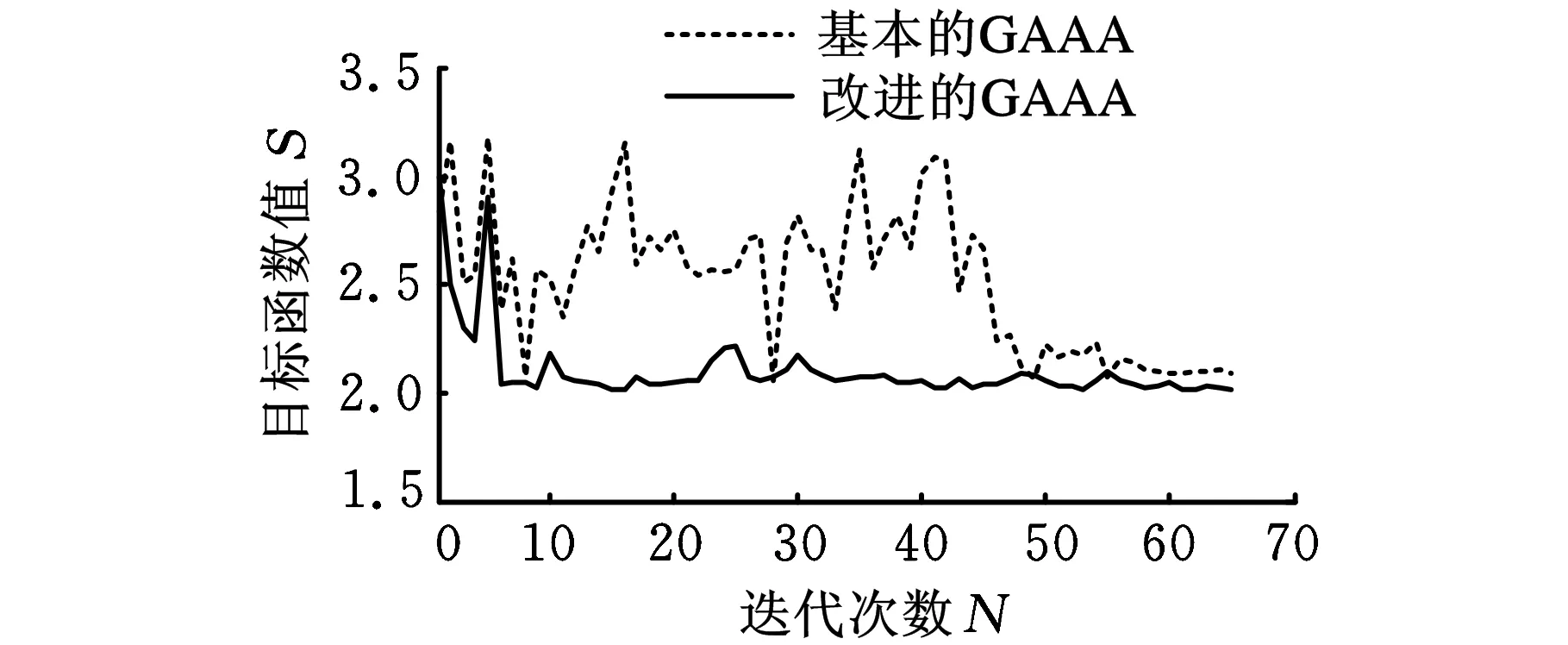
(b)基本的GAAA和改进的GAAA的迭代过程图4　迭代过程

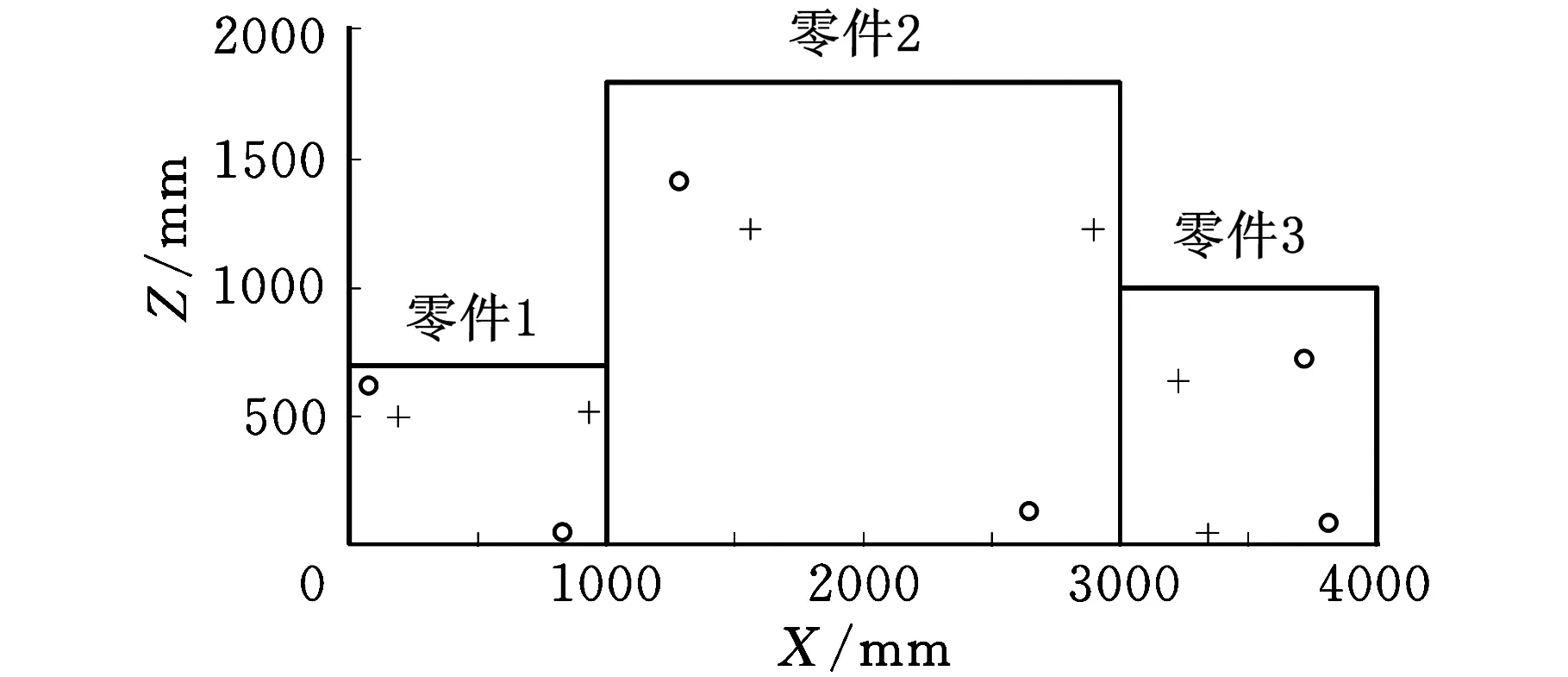
(a)蚁群算法与改进的GAAA求得的最优夹具布局

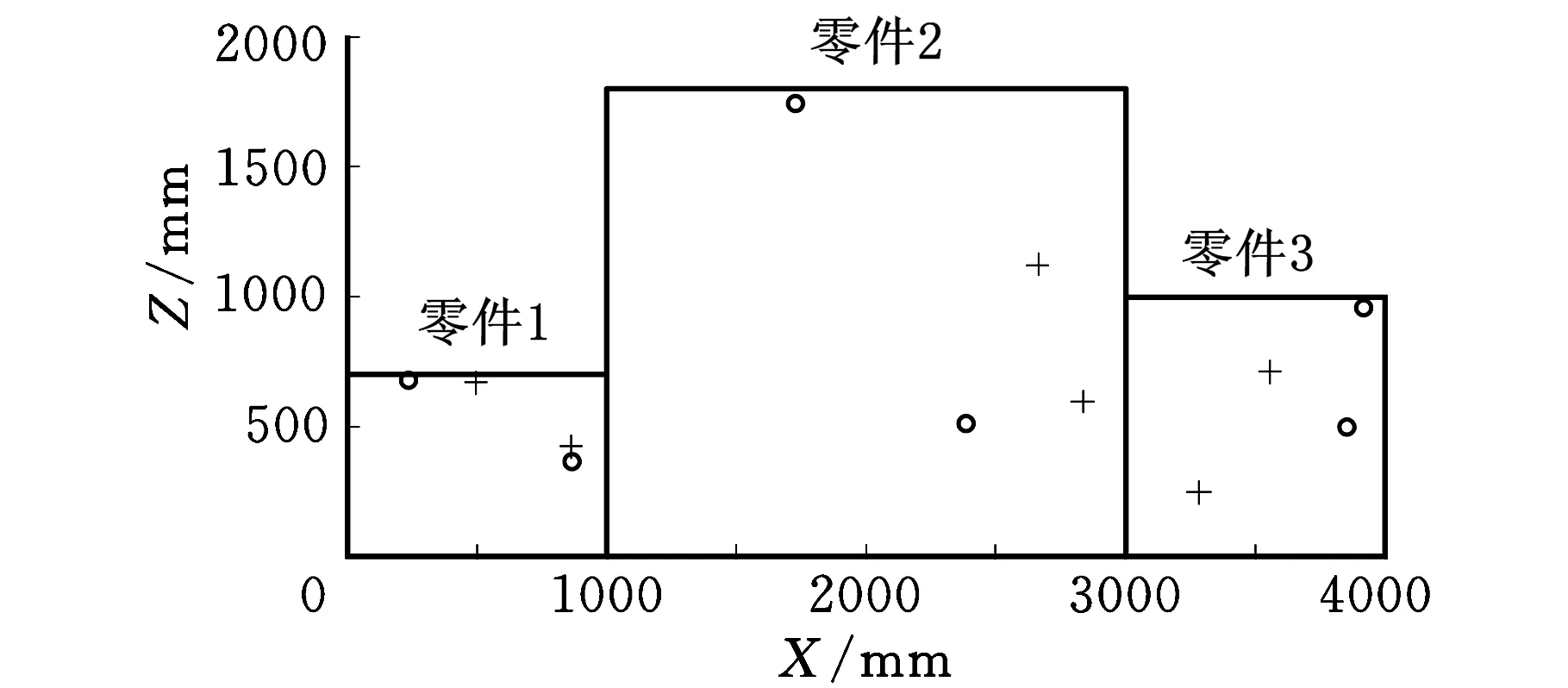
(b)基本的与改进的GAAA求得的最优夹具布局图5　最优夹具布局

图4b、图5b、表3和表4表示在相同参数和相同的初始夹具布局下，基本的GAAA和改进的GAAA求得的结果比较。其中，图4b所示为二者的迭代过程，表3所示为二者求得的最优夹具布局。图5b将表3中PLPs的位置用CAD软件标注在工件上，“+”表示基本的GAAA求得的最优夹具布局，“o”表示改进的GAAA求得的最优夹具布局；表4是二者求得的最小目标函数值。从图4b可以看出，在相同参数和相同的初始夹具布局下，改进的GAAA也比基本的GAAA稳定性好，收敛速度更快，基本的GAAA在大概迭代50次之后趋于稳定，而改进的GAAA在大概迭代30多次之后就趋于稳定，且从表4可以看出，改进的GAAA求得的最小目标函数值2.0126也比蚁群算法求得的结果2.0253要小。

表1　蚁群算法和改进的GAAA求得的最优夹具布局　mm

表2　蚁群算法和改进的GAAA结果比较

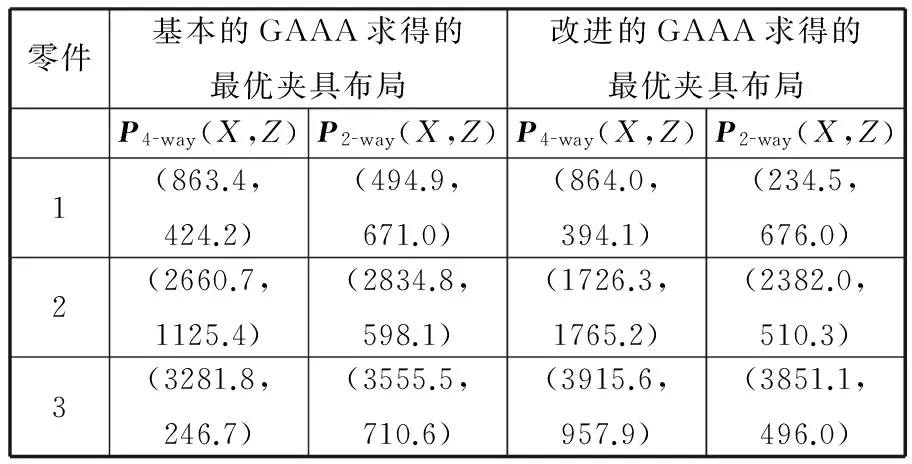
表3　基本的GAAA和改进的GAAA求得的最优夹具布局　mm

表4　基本的GAAA和改进的GAAA结果比较

4　结语

在本文中，分别用改进的GAAA、基本的GAAA以及蚁群算法对多阶段装配过程的夹具布局进行了优化，以找到满足最小目标函数值Smax的最优夹具布局。通过改变遗传算法的变异算子、变异长度以及交叉、变异在蚁群算法中发生的位置，改进了GAAA，提高了GAAA的稳定性和收敛性。在实例分析中可以得出结论：改进的GAAA比基本的GAAA和蚁群算法求得的结果要好，收敛速度更快，稳定性更好。尽管文中对改进的GAAA在设计二维夹具布局方面给了详细描述，但在实际工程应用中，三维零件要比二维的更加实用。所以我们将进一步改进GAAA，来解决多阶段装配过程中三维刚性零件的夹具布局优化问题。

[1]Kim P, Ding Y. Optimal Design of Fixture Layout in Multistation Assembly Processes[J]. IEEE Transactions on Automation Science and Engineering, 2004, 1(2): 133-145.

[2]Izquierdo L E, Hu S J, Jin R, et al. Robust Fixture Layout Design for a Product Family Assembled in a Multistage Reconfigurable Line[J]. Journal of Manufacturing Science and Engineering, 2009, 131(4): 041008.

[3]Huang W, Kong Z, Chennamaraju A. Robust Design for Fixture Layout in Multistation Assembly Systems Using Sequential Space Filling Methods[J]. Journal of computing and information science in engineering, 2010, 10(4): 041001.

[4]Selvakumar S, Arulshri K P, Padmanaban K P, et al. Design and Optimization of Machining Fixture Layout Using ANN and DOE[J]. The International Journal of Advanced Manufacturing Technology, 2013, 65(9/12): 1573-1586.

[5]Wang B F, Nee A Y C. Robust Fixture Layout with the Multi-objective Non-dominated ACO/GA Approach[J]. CIRP Annals-Manufacturing Technology, 2011, 60(1): 183-186.

[6]陈蔚芳, 倪丽君, 王宁生. 夹具布局和夹紧力的优化方法研究[J]. 中国机械工程, 2007, 18(12): 1413-1417.

Chen Weifang, Ni Lijun, Wang Ningsheng. Investigation on Optimization Method for Fixture Layout and Clamping Forces[J]. China Mechanical Engineering. 2007, 18(12): 1413-1417.[7]Padmanaban K P, Prabhaharan G. Dynamic Analysis on Optimal Placement of Fixturing Elements Using Evolutionary Techniques[J]. International Journal of Production Research, 2008, 46(15): 4177-4214. [8]Padmanaban K P, Arulshri K P, Prabhakaran G. Machining Fixture Layout Design Using Ant Colony Algorithm Based Continuous Optimization Method[J]. The International Journal of Advanced Manufacturing Technology, 2009, 45(9/10): 922-934.

[9]Ding Y, Shi J, Ceglarek D. Diagnosability Analysis of Multi-station Manufacturing Processes[J]. Journal of Dynamic Systems, Measurement, and Control, 2002, 124(1): 1-13.

[10]Wang H, Ceglarek D. Variation Propagation Modeling and Analysis at Preliminary Design Phase of Multi-station Assembly Systems[J]. Assembly Automation, 2009, 29(2): 154-166.

[11]Shi J. Stream of Variation Modeling and Analysis for Multistage Manufacturing Processes[M]. Boca Raton:CRC Press, 2010.

[12]Liu J, Jin J, Shi J. State Space Modeling for 3-D Variation Propagation in Rigid-body Multistage Assembly Processes[J]. IEEE Transactions on Automation Science and Engineering, 2010, 7(2): 274-290.

[13]Abellan-Nebot J V, Liu J, Subirón F R, et al. State Space Modeling of Variation Propagation in Multistation Machining Processes Considering Machining-induced Variations[J]. Journal of Manufacturing Science and Engineering, 2012, 134(2): 021002.

[14]丁建立, 陈增强, 袁著祉. 遗传算法与蚂蚁算法的融合[J]. 计算机研究与发展, 2003, 40(9): 1351-1356.

Ding Jianli, Chen Zengqiang, Yuan Zhuzhi. On the Combination of Genetic Algorithm and Ant Algorithm[J]. Journal of Computer Research and Development, 2003, 40(9): 1351-1356.

[15]Ciornei I, Kyriakides E. Hybrid Ant Colony-genetic Algorithm (GAAPI) for Global Continuous Optimization[J]. Systems, Man, and Cybernetics, Part B: IEEE Transactions on Cybernetics, 2012, 42(1): 234-245.

(编辑王艳丽)

Fixture Layout Optimization in Multi-station Assembly Processes Using GAAA

Xie Weisong1Deng Zheng1Ding Bohui2

1.Tianjin University,Tianjin,300072 2.Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education,Tianjin University,Tianjin,300072

GAAA (genetic algorithm-ant colony algorithm) was augmented to solve fixture layout optimization problems of 2D rigid parts in multi-station assembly processes, and the coordinates of two locating pins were properly selected to minimize the sensitivity index. The stability and convergence of GAAA were improved by changing the mutation operator, mutation length of genetic algorithm and the position where crossover and mutation occured in ant colony algorithm. A case about automotive side aperture assembly processes was studied to verify the effectiveness of the augmented GAAA. The results show that the augmented GAAA can generate more accurate results with a faster rate of convergence and a better stability than the basic GAAA and ant colony algorithm.

multi-station assembly process; state space model; fixture layout optimization; genetic algorithm-ant colony algorithm(GAAA)

2014-01-13

国家自然科学基金资助项目(51205286, 51275348)

TH122；TH16< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.05.016

谢伟松，男，1967年生。天津大学理学院副教授。主要研究方向为微分方程数值解、计算几何。邓铮，女，1990年生。天津大学理学院硕士研究生。丁伯慧(通信作者)，女，1976年生。天津大学机械工程学院讲师。