基于组合核函数OSVR算法的起重机减速齿轮箱磨损趋势预测

曹劲然　冯　毅　陆宝春　张登峰　吴　建　石胜征　关德壮

1.南京理工大学，南京，210094　　2.南通润邦重机股份有限公司，南通，226013

基于组合核函数OSVR算法的起重机减速齿轮箱磨损趋势预测

曹劲然1冯毅1陆宝春1张登峰1吴建2石胜征2关德壮2

1.南京理工大学，南京，2100942.南通润邦重机股份有限公司，南通，226013

针对起重机减速齿轮箱的磨损过程具有非线性与时变性，传统磨损趋势预测方法无法有效兼顾预测精度与执行效率的问题，提出了一种基于组合核函数的在线支持向量机回归(online support vector regression，OSVR)预测算法。OSVR的在线学习算法能够适应时间序列的时变性并提高执行效率，同时可利用不同的核函数性能，通过组合模型提高预测精度。采用实际齿轮箱铁谱数据对预测算法进行验证，结果表明，基于组合核函数的OSVR预测算法具有很好的预测精度和适应性，能有效预测起重机齿轮箱的磨损故障，且相比于单一OSVR算法和灰色神经网络组合算法有更高的效率和预测精度。

齿轮箱；磨损趋势预测；在线支持向量机回归；核函数

0　引言

减速齿轮箱是起重机执行起升、变幅、回转等动作的关键传动部件之一。在工作过程中，齿轮箱经常受到重载、冲击和交变载荷的作用，容易发生磨损故障，导致齿轮箱失效[1]。齿轮箱的润滑油中蕴含着丰富的齿轮磨损信息[2]，通过对润滑油的在线油液监测，可以掌握其磨损状态变化规律并提前作出故障预警，所以基于油液监测数据的在线磨损趋势预测对齿轮箱及起重机的安全维护具有重要意义。

目前磨损趋势预测模型主要有灰色模型、时间序列模型和神经网络模型等。文献[3]采用灰色模型对发动机铁谱分析值进行了磨损趋势分析，但该模型只适用于小样本趋势预测，难以预测非线性磨损过程；文献[4]通过自回归求和滑动平均时间序列来预测齿轮箱的非平稳磨损趋势，但预测效率较低，且模型参数确定后不能对非线性时变序列进行跟踪预测；文献[5]将基于BP神经网络的多变量模型应用于航空发动机磨损趋势预测，但同样预测效率低，只适用于离线长期趋势预测。起重机减速齿轮箱的磨损机制复杂，其磨损状态变化往往具有时变性与非线性，因此传统的预测模型难以获得满意的效果；对于复杂时间序列，单一模型预测精度较低，而多模型组合可以提高预测精度[6]。文献[6]提出了一种BP神经网络修正灰色残差的组合模型预测方法，获得了较好的预测结果，但神经网络训练过程易陷入局部最小，且预测结果不稳定。支持向量回归(support vector regression，SVR)算法能有效解决小样本、非线性、高维数和局部极小等问题[7]，而且随着在线SVR算法的研究与发展，在线最小二乘SVR、OSVR等能够在线学习并动态调整模型参数，具有在线自适应性[8]。针对起重机齿轮箱的磨损趋势预测问题，本文提出一种组合核函数的OSVR算法，利用支持向量机局部核函数与全局核函数的特性，先采用全局核函数OSVR算法在线预测整体趋势，再用局部核函数OSVR算法对残差进行实时修正，从而提高总体预测精度与效率。

1　算法理论基础

1.1支持向量回归原理

将支持向量机推广到非线性回归估计中，称为回归型支持向量机。T为给定数据集：

T={(xi,yi)|xi∈Rd,yi∈R,i=1,2,…,n}

把输入样本通过φ(·)非线性映射到高维特征空间，构造回归函数为

f(x)=(w·φ(x))+b

(1)

其中，w∈Rd，b∈R，可以通过求解如下凸二次规划问题得到：

(2)

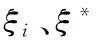
引入拉格朗日乘子可将原凸二次规划问题(式(2))转化为对偶二次规划问题：

(3)

Qij=φ(xi)Tφ(xj)=K(xi,xj)

(4)

1.2OSVR在线学习算法

普通的SVR模型是在离线情况下对数据集进行批量训练的，效率较低，而基于增量式在线学习的OSVR模型是逐一加入新数据进行优化训练的，当数据在线更新时，能够通过增加或删除一个样本实现模型的动态调整[9]。

(5)

根据h(xi)与θi的情况可以将样本分为三个子集，即支持向量集S、错误支持向量集E和样本保留集R：

(6)

增量式在线学习算法包括递增算法和递减算法。递增算法的基本思想是当新样本加入训练集{xc,yc}时，需要对新样本加入θc，并逐步调整θi和θc使新样本加入式(6)中的三个集合之一，同时要使所有样本满足KKT条件。具体方法是：当|h(xc)|<ε时，新样本加入R集，原样本集的θi不需改变；当|h(xc)| ≥ε时，新样本加入S集或E集，加入前应确保原样本仍满足KKT条件，否则对原有集合作样本移动，直至所有样本满足KKT条件。递减算法的基本思想与递增算法类似，即遗忘训练集中的一些样本，然后通过调整剩余样本的参数使其满足KKT条件。由此可以实现SVR模型的动态调整以及训练样本的在线更新。

1.3相空间重构理论

Takens[10]的相空间重构理论中提出，系统中任一分量的演化是由与之相互作用的其他分量决定的，因此起重机齿轮箱的磨损时间序列应该隐含着齿轮箱的摩擦学运动规律。根据相空间重构理论，假设观测到的时间序列为{x(k),k=1,2,…,N}，重构相空间后的状态向量可表示为

X(k)=(x(k),x(k-τ),…,x(k-(m-1)τ))

(7)

式中，τ为延迟时间；m为嵌入维数(即重构相空间维数)。

由Takens定理可知，复杂非线性时间序列预测的实质便是通过运动系统的状态逆向重构原系统的模型，所以对下一步进行预测就是构建以下预测模型：

X(k+τ)=F(X(k))

(8)

其中，F(·)是重构的预测模型，即通过相空间重构方法将非线性时间序列映射到了高维空间。而支持向量机能有效解决非线性、高维数等问题，因此将重构预测模型与支持向量回归模型结合起来可以有效提高时间序列的预测精度。

1.4核函数的类型及影响

支持向量机通过核函数的内积映射，将高维特征空间的运算问题转化到原始空间进行，因此核函数决定了支持向量机的非线性映射能力，而核函数类型及其参数的确定会对SVR模型产生不同的影响。核函数主要可分为两种类型，即局部核函数与全局核函数。核函数的常用形式有三种：多项式核函数(polynomial)、径向基核函数(RBF)、Sigmoid核函数。根据文献[11]分类方法，一般多项式核函数属于全局核函数，径向基核函数与Sigmoid核函数都属于局部核函数。

核函数映射形式的不同会导致全局核函数与局部核函数的外推能力与学习能力等函数特性也有所区别。全局核函数能够获取待预测样本较大范围内的全局信息，具有较强的外推能力，但学习能力较弱；局部核函数能够有效提取样本点附近的信息，有较强的非线性逼近能力，但外推能力较弱。对于磨损趋势预测的在线建模问题，单一的核函数SVR模型在预测能力上有局限性，因此本文考虑将两种互补性的核函数模型组合起来，充分利用两种核函数的优点，提高预测精度。

2　基于组合核函数的OSVR算法

2.1算法基本思路

一般核函数组合的方式是将两种类型核函数加权组合，构造新的组合核函数后进行建模和预测，但对于在线动态建模问题，采用该方式权值较难确定。因此本文决定采用基于两种类型核函数的OSVR模型同时预测，首先通过基于全局核函数的OSVR模型在线预测当前样本的整体趋势走向，再对预测结果的残差进行相空间重构，并通过基于局部核函数的OSVR模型对残差进行预测，最后将预测的残差实时修正全局核函数OSVR模型的预测值，从而实现组合核函数的OSVR算法在线预测。

首先考虑单步预测。假设在线建模时，当前数据窗口中的时间序列为{xt,t=1,2,…,n}，预测目标值为{xn+1}。首先对当前时间序列进行相空间重构，若嵌入维数为m，则可建立映射Rm→R，表示输入x={xt,xt-1,…,xt-m-1}与输出y={xn+1}之间的映射关系，并扩充为矩阵的形式即获得SVR模型的训练样本：

(9)

对训练样本按照如下的回归函数，采用OSVR算法在线训练：

(10)

t=m+1,m+2,…,n

(11)

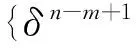
(12)

式中，Kδ(·)为局部核函数，一般选用RBF核函数。

因此对于非线性时变的时间序列{xt,t=1,2,…,n+1}，一定可以分解为一个平滑的趋势项序列与一个去趋势项的非线性序列，即

(13)

i=m+1,m+2,…,n

(14)

确定了一步预测的方法之后，利用递推预测和滚动优化的思想，可以将其推广到N步预测。若当前时间序列{xt,t=1,2,…,n}的N步预测目标值为{xn+1,xn+2,…,xn+N}，其中，N小于嵌入维数m，则N步预测问题可以表示成如下的连续单步预测问题：

(15)

即在嵌入维数m的步数内，将上一步的预测值代入到原训练模型中代替新样本更新，然后以此为基础继续预测下步预测值，如此循环来实现N步预测。

2.2算法具体流程图

将不同特性的核函数组合的OSVR预测模型相对于单一的OSVR模型预测精度会有所提高，同时OSVR在线的增量与减量学习算法相比于传统SVR模型效率也有所提高。基本的算法流程如图1所示。

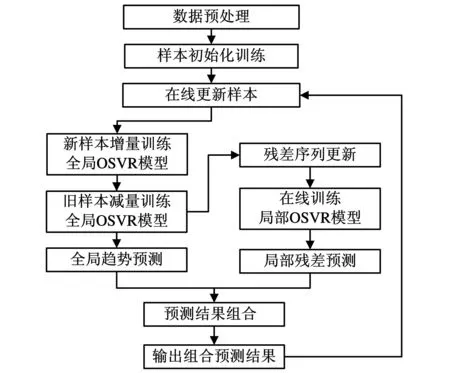
图1　在线预测流程图

2.3算法具体实现步骤

(1)首先对数据预处理，通过相空间重构方法构造初始训练样本。

(2)初始化训练全局OSVR模型，并用训练的残差初始化训练局部OSVR模型。

(3)在线更新窗口时间序列{xt,t=1,2,…,n}，经过相空间重构得到新样本，用全局OSVR模型在线训练，在线训练包括对新样本的增量训练和旧样本的减量训练。

(5)同步更新全局OSVR模型的残差，经相空间重构后用局部OSVR模型在线训练残差序列。

(9)输入新序列值xn+1，重复步骤(3)～步骤(9)，实现连续N步预测。

3　组合核函数OSVR模型在起重机减速齿轮箱磨损趋势预测中的应用

为了验证组合核函数OSVR模型在磨损趋势预测中的效果，以某大型起重机用的主起升减速齿轮箱润滑油的铁谱监测数据为例，对采集到的铁元素含量的时间序列进行在线预测。仿真实验环境为普通台式电脑，CPU为i5-3470，3.20GHz，内存2GB，软件平台为MATLAB7.0。

可以看出齿轮箱工作一段时间后产生了剧烈磨损，因此磨粒的监测序列有较强的非线性与时变特征，具有一定随机性和突变性，通过在线预测可以提前发现磨损异常，进而作出相关检查与维护。为了便于预测算法的运算以及后续不同算法比较，首先对原始数据作归一化处理。之后给出具体模型预测参数：全局核函数OSVR算法选用多项式核函数，p=2，ε1=0.1，C1=1000；局部核函数OSVR算法选用RBF核函数，σ=0.2，ε2=0.01，C2=1000。在线时间序列的长度n与嵌入维数m对于时间序列的预测精度和效率起着关键作用。采用最终误差预报准则结合交叉验证[12]的方法确定最佳在线时间序列的在线建模长度n1=13、嵌入维数m1=5，进而确定邻域残差序列的建模长度n2=8、嵌入维数m2=5。样本数据为46个，用前13个数据作为初始训练样本，通过实时更新，在线单步预测之后的14～46个数据。其单步预测值与原始值如图2所示，虚线左侧为初始训练数据，右侧为预测值与原始数据。

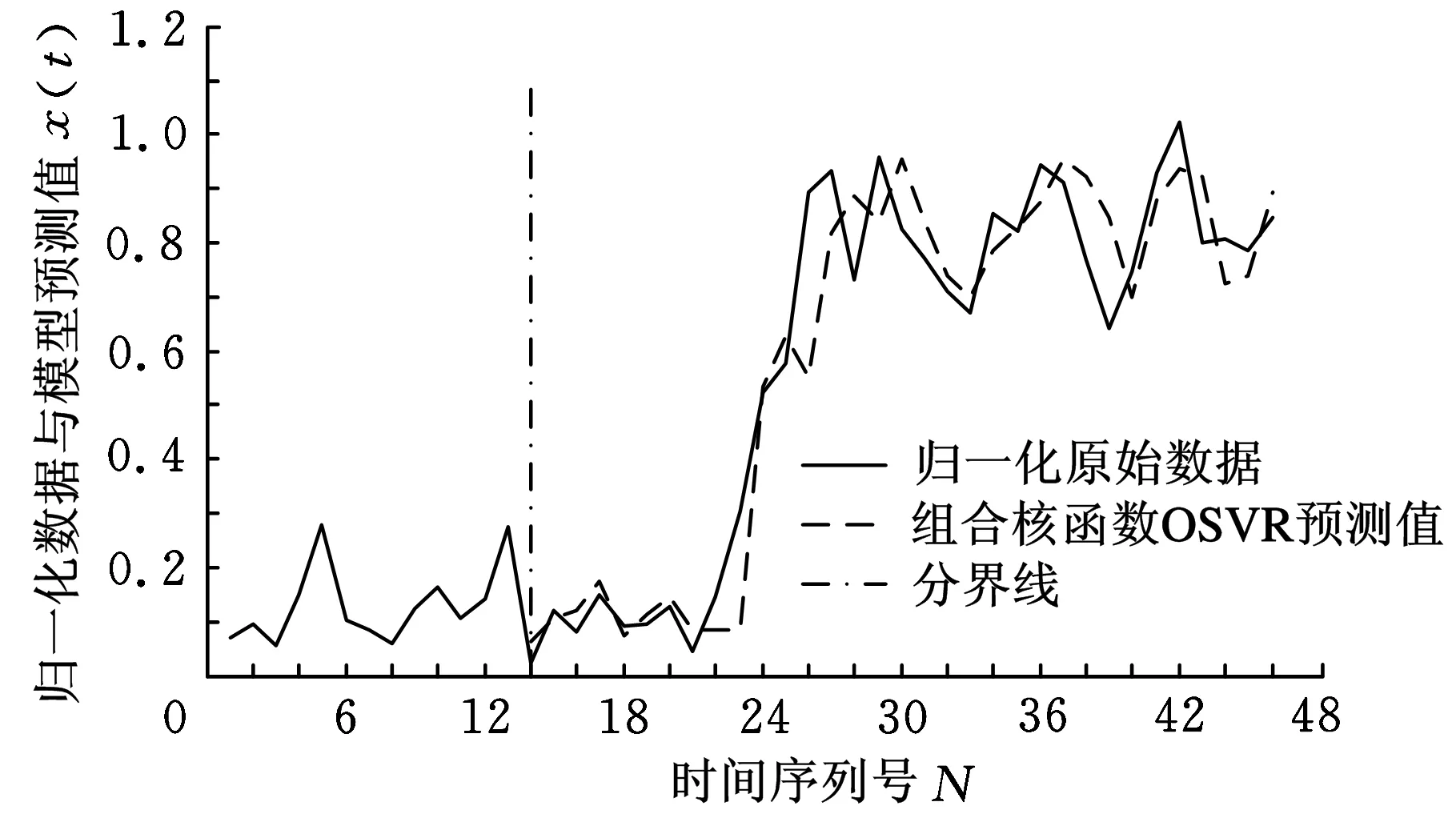
图2　组合核函数OSVR算法预测结果

从图2可以看出原始数据初始状态平稳，在第23个样本后有急剧上升趋势，在第30个样本之后波动较大，而在此过程中模型很好地跟踪预测了磨粒监测的单步变化情况。由于是在线样本实时滚动建模，所以历史数据影响较小，采用的组合核函数OSVR算法能动态修正模型参数适应数据变化，说明模型具有较强的在线自适应能力及较好的预测精度。

为了比较新算法性能，采用单一核函数OSVR算法和灰色BP神经网络(GMBP)组合算法[6]对相同序列在线对比预测，其中单一核函数OSVR算法分别采用全局核函数模型与局部核函数模型，全局核函数选用多项式核函数，局部核函数选用RBF核函数，其余参数设置与上文组合核函数中的相关参数相同；GMBP组合算法的参数选取参考文献[6]，趋势项模型为新陈代谢GM(1,1)模型， 残差模型为5×20×1的BP神经网络模型，输入层、隐含层采用tansig函数，输出层采用purelin函数。采用三种算法对后33个样本做单步预测并与新算法对比，结果如图3所示。

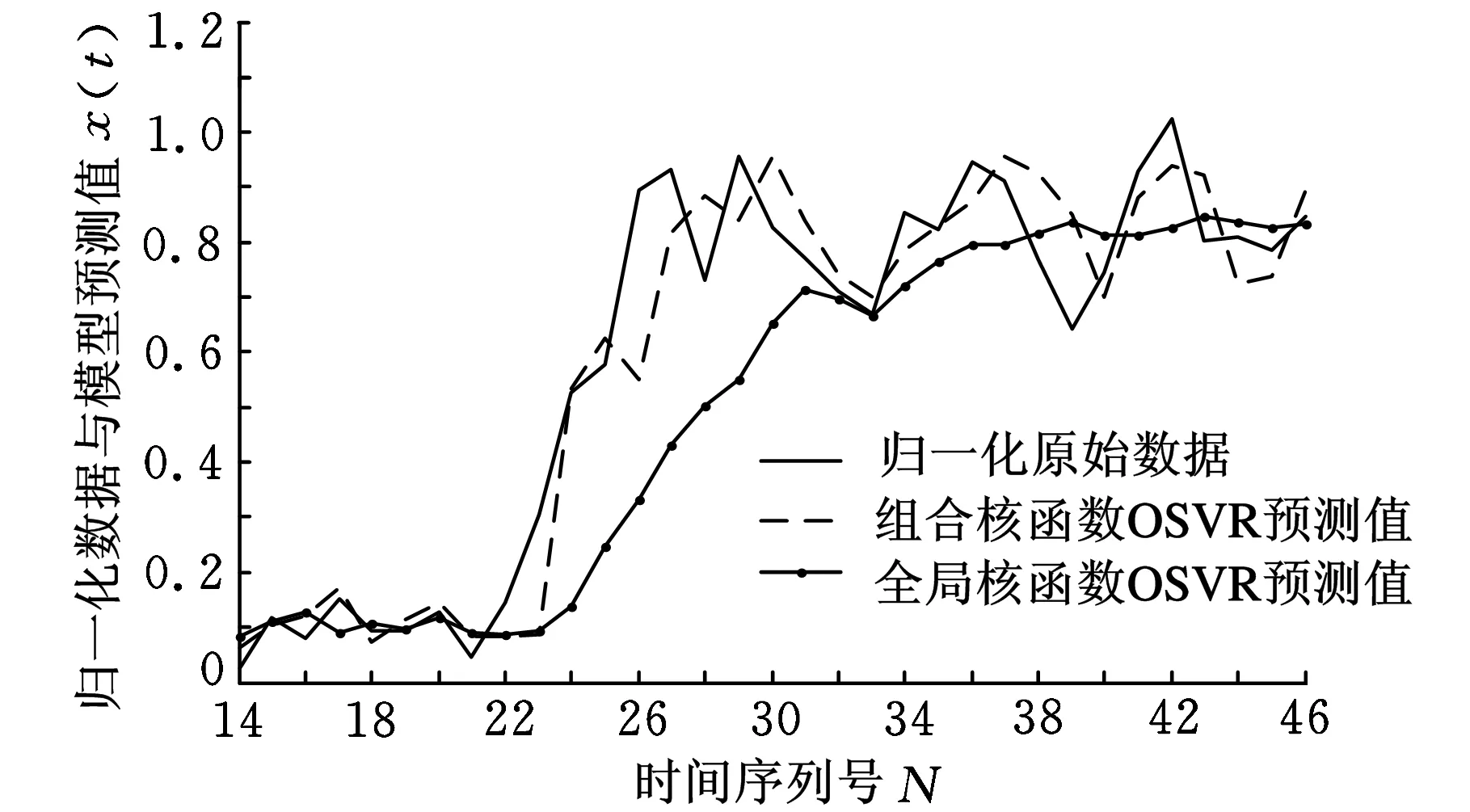
(a)全局核函数OSVR模型与新模型预测结果对比

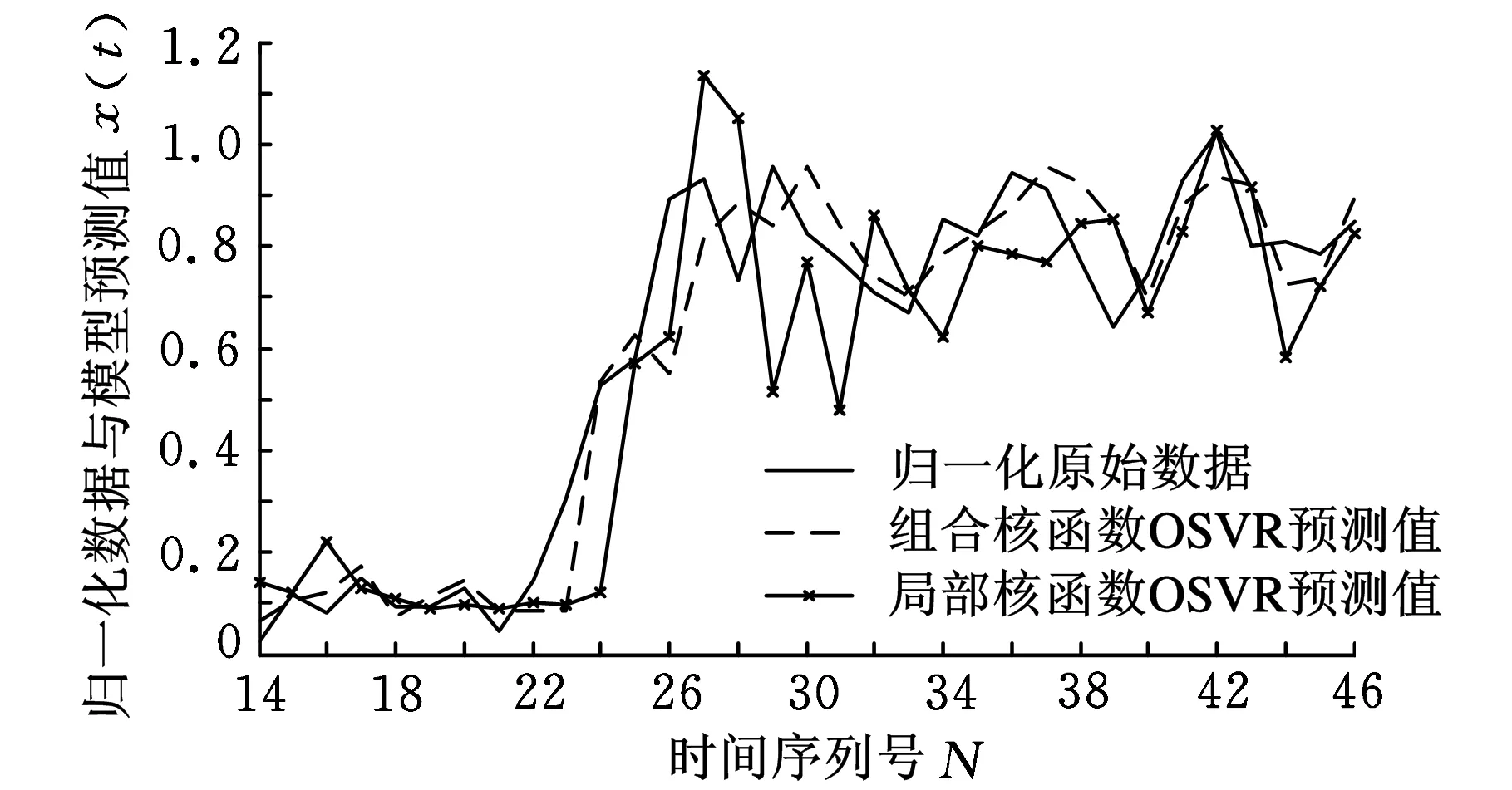
(b)局部核函数OSVR模型与新模型预测结果对比

(c)GMBP模型与新模型预测结果对比图3　各模型预测结果对比

从图3可以看出，全局核函数OSVR模型的预测值虽然能预测出原始数据总体趋势，但对数据的波动不敏感，在数据转折或大幅变化时不能做出较为准确的预判，预测误差较大；局部核函数OSVR模型能够对故障数据的大幅变化趋势做出相对准确的预测，但对于局部非线性较弱的数据反而出现过训练的情况，有较大偏差；GMBP组合模型的预测值总体能贴合原始数据趋势，但仍比组合核函数OSVR模型的波动性大，且每次预测值不稳定，与原始数据贴合程度比新算法低。

为了全面比较与衡量算法的性能，采用平均绝对误差eMAE与标准均方根误差eNRMSE作为衡量性能的指标：

(16)

(17)

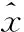
预测结果的衡量指标比较如表1所示。

表1　预测结果对比

表1中组合核函数OSVR算法的平均绝对误差与标准均方根误差最小，由eMAE指标可见在预测精度上较全局核函数OSVR算法提高了46%，较局部核函数OSVR算法提高25%，较GMBP组合算法提高31%；组合核函数OSVR算法的eNRMSE指标最小，即该算法的预测曲线最贴合原始曲线。在执行效率方面虽然全局核函数执行速度最快，用时0.7734s，但相对的eMAE与eNRMSE最大，即预测精度与拟合程度最低；GMBP组合算法由于BP神经网络的在线训练耗时较多，所以在线预测的执行效率最低；组合核函数OSVR算法比局部核函数(RBF核函数)OSVR模型稍快一点，原因在于单一的局部核函数OSVR算法的在线样本规模较大且计算复杂，而全局核函数OSVR预测时支持向量较少，且残差序列规模也比较小，计算复杂度相对较低，因此执行效率会有所提高。组合核函数OSVR算法的单步平均预测时间为0.0398s，远小于原始数据单个样本采样时间，完全可以实现在线预测。综合比较来看，组合核函数OSVR算法能够在保证预测效率的同时具有最高的预测精度，完全能对非线性时变的磨损时间序列进行在线预测，并为起重机减速齿轮箱磨损故障预报提供有力依据。

4　结语

本文针对起重机减速齿轮箱的磨损趋势预测提出了一种组合核函数OSVR算法，采用OSVR的增量式学习算法使预测模型能够在线动态调整模型参数，并将不同特性核函数的OSVR预测模型以残差补偿的形式组合，在保证算法预测效率的同时提高了预测精度。实验研究说明组合核函数OSVR算法有较强的在线自适应能力，即使监测的金属元素含量急剧变化与波动仍能快速有效地跟踪预测，在预测性能上优于单一核函数模型和GMBP组合模型，对于起重机减速齿轮箱的在线故障预测有一定的参考价值。后续研究将讨论算法中组合核函数OSVR模型中各参数的最优选取问题以及对于核函数非线性组合的情况下预测效果问题。

[1]时均莲,刘卓,乔新燃,等.海上平台起重机齿轮箱零部件失效形式分析及对策[J].起重运输机械,2012(7):73-76.

ShiJunlian,LiuZhuo,QiaoXinran,etal.OffshoreCraneGearboxPartsFailureAnalysisandCountermeas-ures[J].HoistingandConveyingMachinery,2012(7):73-76.

[2]陈宏军,涂群章.基于油液分析的在线磨损监测技术研究现状与发展趋势[J]. 矿山机械,2008(24):22-25.

ChenHongjun,TuQunzhang.CurrentResearchandDevelopmentoftheOn-lineAbrasionMonitoringTechniqueBasedonOilAnalysis[J].Mining&ProcessingEquipment, 2008(24):22-25.

[3]张菊,钟新辉,张峰.灰色系统在发动机铁谱分析监测中的应用[J].内燃机,2013(3):39-40,53.

ZhangJu,ZhongXinhui,ZhangFeng.ApplicationofGraySysteminEngineFerrographyMonitoring[J].InternalCombustionEngines,2013(3):39-40,53.

[4]王金涛,吕晓军,谢友柏,等.在线铁谱监测系统中的非平稳磨损趋势分析[J].西安交通大学学报,2003,37(5):463-466.

WangJintao,LüXiaojun,XieYoubai,etal.NonstationaryWearTrendAnalysisMethodinOn-LineFerrographMonitoringSystem[J].JournalofXi'anJiaotongUniversity,2003,37(5):463-466.

[5]陈果,杨虞微.航空发动机复杂磨损趋势的神经网络多变量预测模型[J].中国机械工程,2007,18(1):70-74.

ChenGuo，YangYuwei.ArtificialNeuralNetworkMulti-variableForecastingModelofAero-engineComplexWearTrend[J].ChinaMechanicalEngineering, 2007,18(1):70-74.

[6]刘玉兵,陈亚忠,王晓东,等.BP神经网络修正灰色残差组合模型方法在油液光谱分析中应用的研究[J].润滑与密封,2007,32(3):172-174.

LiuYubing，ChenYazhong，WangXiaodong，etal.ResearchonOilSpectralAnalysisPredictionBasedonRemnantDifferenceCorrectCombinedModelofBPNeuralNetwork[J].LubricationEngineering, 2007, 32(3): 172-174.

[7]DebasishB，SrimantaP，DipakCP．SupportVectorRegression[J].NeuralInformationProcessing-LettersandReviews, 2008,11(10):203-224.

[8]刘大同,彭宇,彭喜元,等.基于残差预测修正的局部在线时间序列预测方法[J].电子学报,2008,36(12A):81-85.

LiuDatong，PengYu，PengXiyuan，etal.LocalOnlineTimeSeriesPredictionBasedontheResidualCompensationwithOnlineSVR[J].ActaElectronicaSinica,2008,36(12A):81-85.

[9]GiovanniM，FrancescoP.LearningtoTradewithIncrementalSupportVectorRegression[J].LectureNotesinComputerScience,2008,5271:591-598.

[10]TakensF.DetectingStrangeAttractorinTurbulence[J].LectureNotesinMathematics, 1981, 898(2): 361-381.

[11]张芬,陶亮,孙艳.基于混合核函数的SVM及其应用[J].计算机技术与发展,2006, 16(2):176-178.

ZhangFen,TaoLiang,SunYan.SVMandItsApplicationBasedonMixturesofKernels[J].ComputerTechnologyandDevelopment,2006, 16(2):176-178.

[12]王旭辉,黄圣国,曹力,等.基于LS-SVM的航空发动机气路参数趋势在线预测[J].吉林大学学报(工学版),2008,38(1):239-244.

WangXuhui，HuangShengguo，CaoLi，etal.LS-SVMBasedOnlineTrendPredictionofGasPathParametersofAeroEngine[J].JournalofJilinUniversity(EngineeringandTechnologyEdition),2008, 38(1):239-244.

(编辑王艳丽)

Wear Trend Prediction of Crane Gearbox Based on OSVR Method with Combined Kernel Functions

Cao Jinran1Feng Yi1Lu Baochun1Zhang Dengfeng1Wu Jian2Shi Shengzheng2Guan Dezhuang2

1.Nanjing University of Science and Technology，Nanjing，210094 2.Nantong Rainbow Heavy Machine Company，Nantong，Jiangsu,226013

For the nonlinear and nonstationary crane gearbox wear process, prediction precision and efficiency cannot be effectively balanced by using traditional prediction methods. An OSVR prediction method based on combined kernel functions was proposed. The OSVR algorithm can be adapted to time-varying time series and the efficiency can be improved. Simultaneously, the kernel-combined model would be able to improve the prediction accuracy. Experimental results show that the trend of the crane gearbox wear process can be predicted effectively by using the new method, and the prediction is more accurate than the results of the OSVR method with single kernel function and the gray-neural network method.

gearbox; wear trend prediction;online support vector regression(OSVR); kernel function

2013-12-17

国家自然科学基金资助项目(51275245，61374133)

TP181DOI：10.3969/j.issn.1004-132X.2015.05.013

曹劲然，男，1989年生。南京理工大学机械工程学院博士研究生。主要研究方向为大型工程机械故障诊断与预测。冯毅，男，1989年生。南京理工大学机械工程学院博士研究生。陆宝春，男，1965年生。南京理工大学机械工程学院教授、博士研究生导师。张登峰，男，1973年生。南京理工大学机械工程学院副研究员、博士研究生导师。吴建，男，1967年生。南通润邦重机有限公司董事长。石胜征，男，1971年生。南通润邦重机有限公司海工技术总监。关德壮，男，1969年生。南通润邦重机有限公司设计部主任。