AZ31B镁合金断裂应变与应力三轴度的关系研究

周梦成　冯　飞　胡建华　雷　雨　何　鹏　黄尚宇　邹方利

武汉理工大学,武汉,430070

AZ31B镁合金断裂应变与应力三轴度的关系研究

周梦成冯飞胡建华雷雨何鹏黄尚宇邹方利

武汉理工大学,武汉,430070

对AZ31B镁合金光滑圆棒和缺口圆棒进行了系列准静态拉伸试验,采用ABAQUS对各试样拉伸过程进行了模拟分析。拟合得到了Johnson-Cook断裂失效模型的部分材料常数，建立了AZ31B镁合金断裂应变与应力三轴度的关系模型。将建立的失效模型输入到ABAQUS中进行仿真模拟，模拟结果与试验结果基本一致，验证了断裂失效模型的正确性。

AZ31B镁合金;准静态拉伸试验;Johnson-Cook失效模型;有限元模拟

0　引言

镁合金是目前最轻的金属结构材料之一[1],由于节能环保的需要，镁合金在汽车、航空航天以及电子行业等领域的应用日益广泛[2-3]。镁合金的本构和失效模型是分析其塑性变形过程、失效断裂行为以及预测其成形缺陷的重要理论基础与前提，而材料的失效参量是描述材料失效行为的一个重要方面。金属材料塑性变形和断裂失效特征与应变、应变率及温度有关，许多研究结果表明，应力三轴度对材料的失效参量有很大影响[4-6]。在镁合金塑性加工过程中，构件各点的应力三轴度均不相同，且还随时间变化而改变，当应力达到其抗拉强度时，构件会发生局部颈缩,进而产生裂纹直至失效断裂。要深入研究镁合金塑性变形及失效行为，必须要建立其断裂失效模型，而断裂应变与应力三轴度的关系是失效模型的核心。因此，研究镁合金断裂应变与应力三轴度的关系，从而建立其失效断裂模型，对分析镁合金塑性成形及失效过程，优化工艺参数和预测成形缺陷具有重要理论意义和应用价值。

近年来，随着有限元方法的快速发展，许多科研工作者采用有限元数值模拟法来确定金属材料的本构方程参数和失效参量。文献[7-8]通过试验和有限元模拟研究了应力三轴度和应变率对结构钢变形行为的影响。文献[9]以45钢为研究对象,考察了应力三轴度、温度和应变率对材料失效应变的影响，计算了45钢Johnson-Cook损伤失效参量。文献[10]研究了应力三轴度和应变率对6063 铝合金力学性能的影响，研究结果表明,随着应力三轴度的减小，等效断裂应变增大。文献[11-12]建立了7A04和2A12铝合金Johnson-Cook的本构关系和失效模型,试验结果表明,两种铝合金失效应变均随温度的升高、应力三轴度的减小而增大。

上述研究表明,应力三轴度对金属材料的塑性变形和失效断裂行为有很大的影响,Johnson-Cook损伤模型能有效描述金属材料在高温、高应变率条件下的力学行为。而断裂应变与应力三轴度的关系是Johnson-Cook断裂模型的核心部分。鉴于此,本文以AZ31B镁合金为研究对象，通过准静态拉伸试验,结合有限元模拟方法，研究AZ31B镁合金断裂应变与应力三轴度的关系。首先对光滑圆棒和缺口圆棒四类试样进行一系列的准静态拉伸试验,然后采用ABAQUS对各试样拉伸过程进行仿真模拟，通过其中三组试样的数据计算得到Johnson-Cook断裂失效模型部分参数，建立AZ31B镁合金断裂应变与应力三轴度的关系模型，最后用得到的模型对剩下的一组试样拉伸过程进行仿真模拟,验证模型的正确性。

1　拉伸试验及模拟

1.1试验材料及设备

试验所用材料为AZ31B镁合金交叉轧制板材,板厚12 mm,其元素的质量分数见表1。根据试验需要,将试样加工成图1所示的四种规格形式，分别为光滑试样及缺口半径为1 mm、2 mm、4 mm的试样，试样总长度为150 mm,有效尺寸为φ4 mm×60 mm。为了保证试验的准确性和可重复性，每类试样均进行了3组有效试验。AZ31B镁合金的准静态拉伸试验是在Series IX万能拉伸机上进行的，试验拉伸速度为5 mm/min。

表1　试验用AZ31B镁合金板材化学成分(质量分数)　%

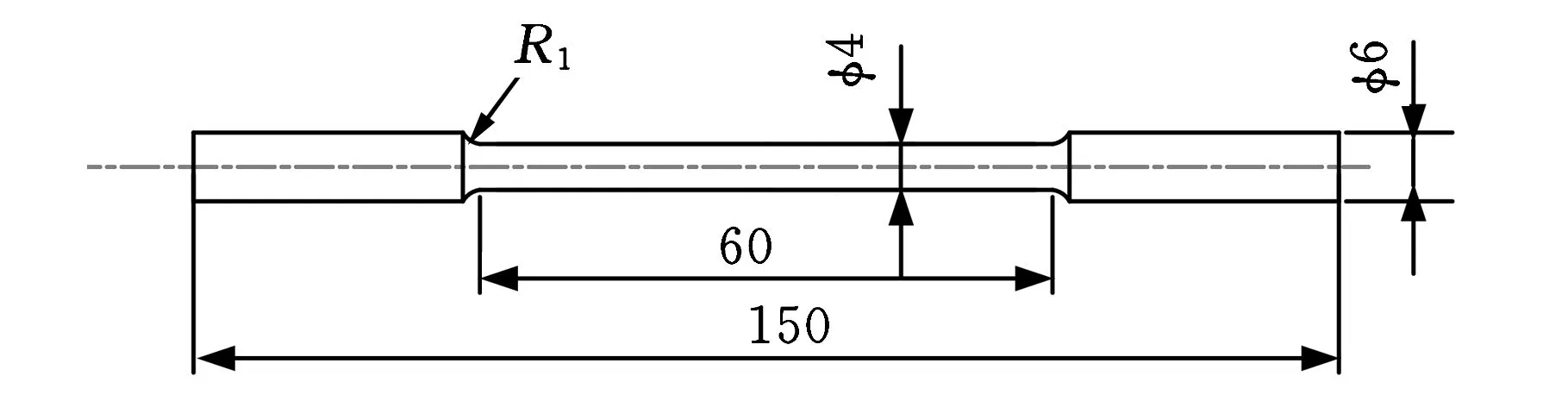
(a)光滑试样

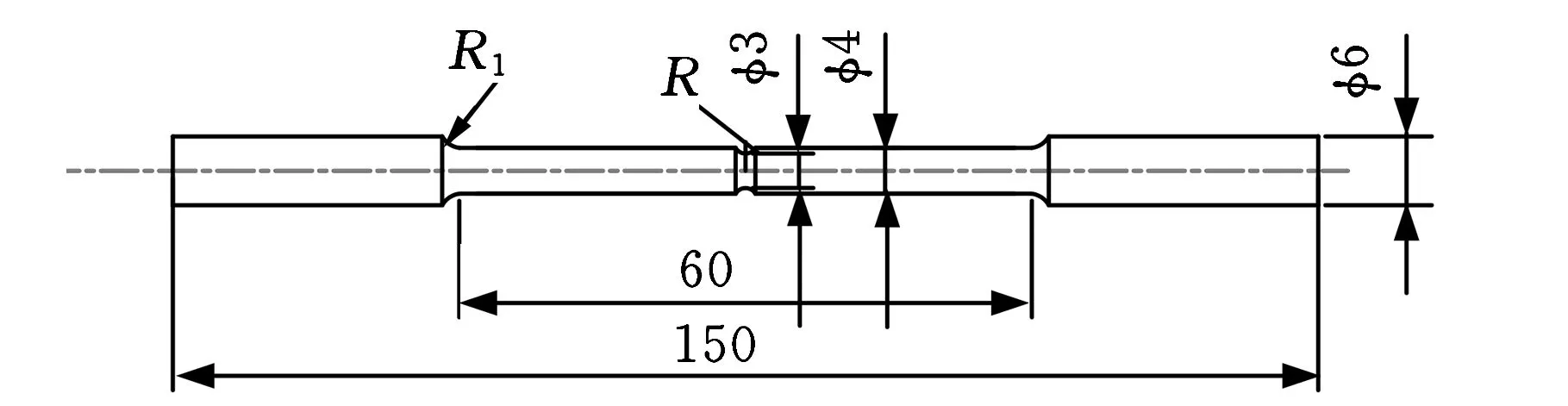
(b)缺口试样图1　试样形状尺寸

1.2准静态拉伸试验结果及分析

试验得到各试样工程应力-应变曲线见图2,拉断后的试样如图3所示。缺口半径R增大，意味着应力三轴度减小，由图2可知，随着缺口半径R的增大(光滑试样可认为缺口半径为无穷大),即随着应力三轴度减小,AZ31B镁合金的等效弹性模量减小,工程应力应变逐渐减小(应力应变曲线依次逐渐降低),说明其等效屈服应力也在减小。由图3可看出,试样被拉断的过程中几乎没有颈缩,说明AZ31B镁合金在室温下具有较大的脆性。

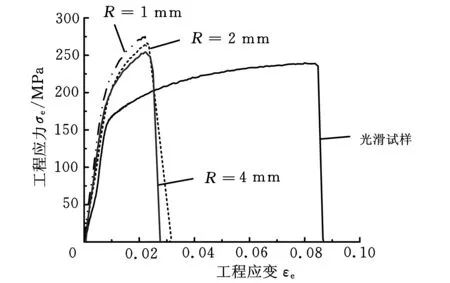
图2　各试样工程应力应变曲线图

(a)光滑试样(b)R=2 mm

(c)R=1 mm(d)R=4 mm图3　拉断后的各类试样

1.3有限元模拟计算

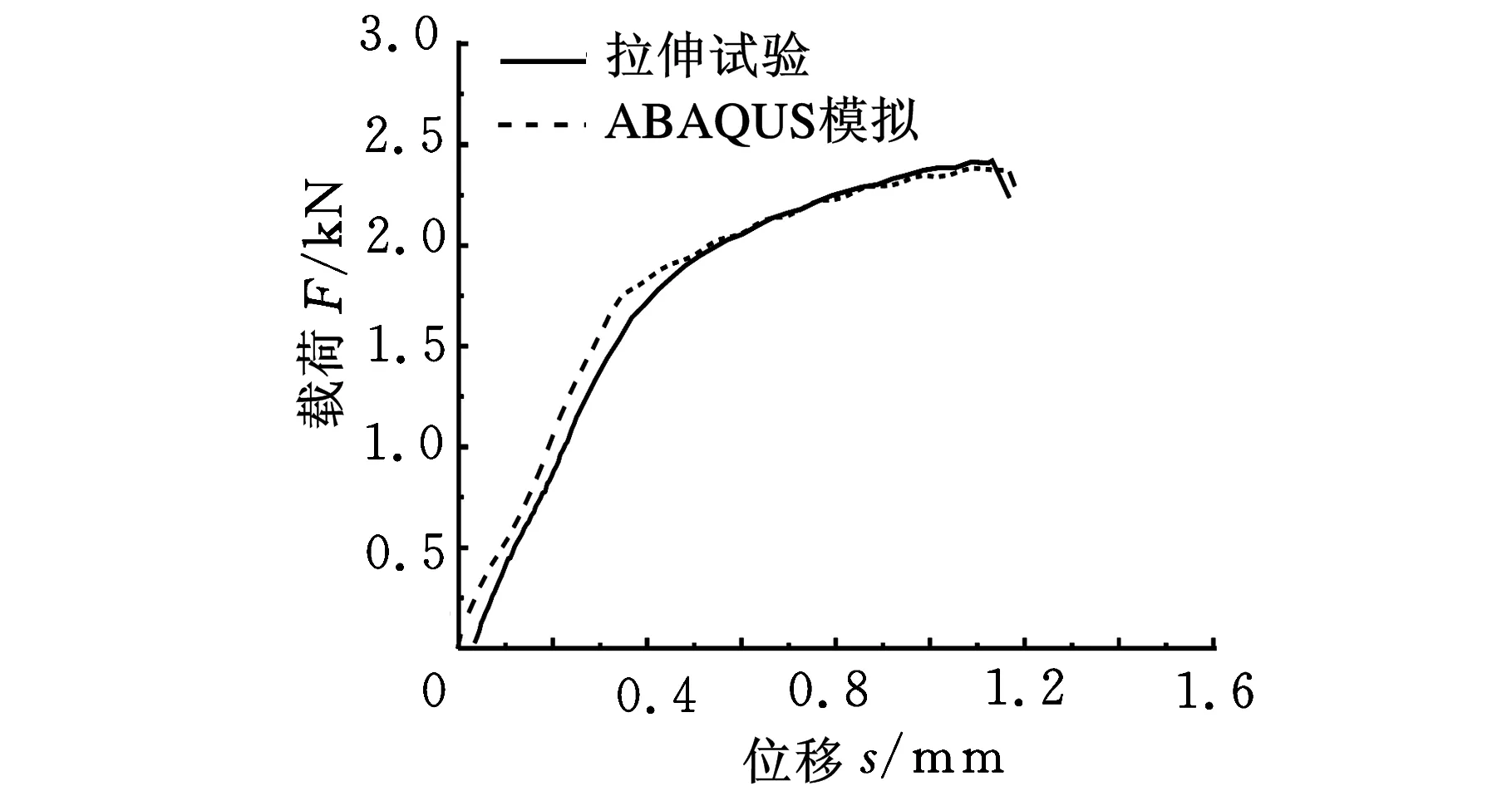
AZ31B镁合金材料特性参数如下：密度1780 kg/m3,弹性模量45GPa,泊松比0.34。将AZ31B镁合金材料特性参数以及试验测得的真实应力-应变输入到ABAQUS中,对各试样拉伸过程进行仿真模拟,模型单元类型为C3D8R,为了保证计算精度，划分网格时,对缺口处网格进行细化。轴对称模型的边界条件为一端固定，另一端施加恒定的轴向拉伸速度(v=5 mm/min)。图4所示为光滑圆棒和缺口半径分别为1 mm、4 mm圆棒试样有限元模型,图5为各试样试验和经有限元计算得到的载荷-位移曲线。由图5可知，有限元模拟计算得到的各试样载荷-位移曲线与试验结果十分吻合，说明有限元迭代计算可以较准确地预测各试样的试验结果。

(a)光滑试样

(b)R=1 mm试样

(a)光滑试样

(b)缺口半径R=1 mm试样

(c)缺口半径R=4 mm试样
图4各试样有限元模型

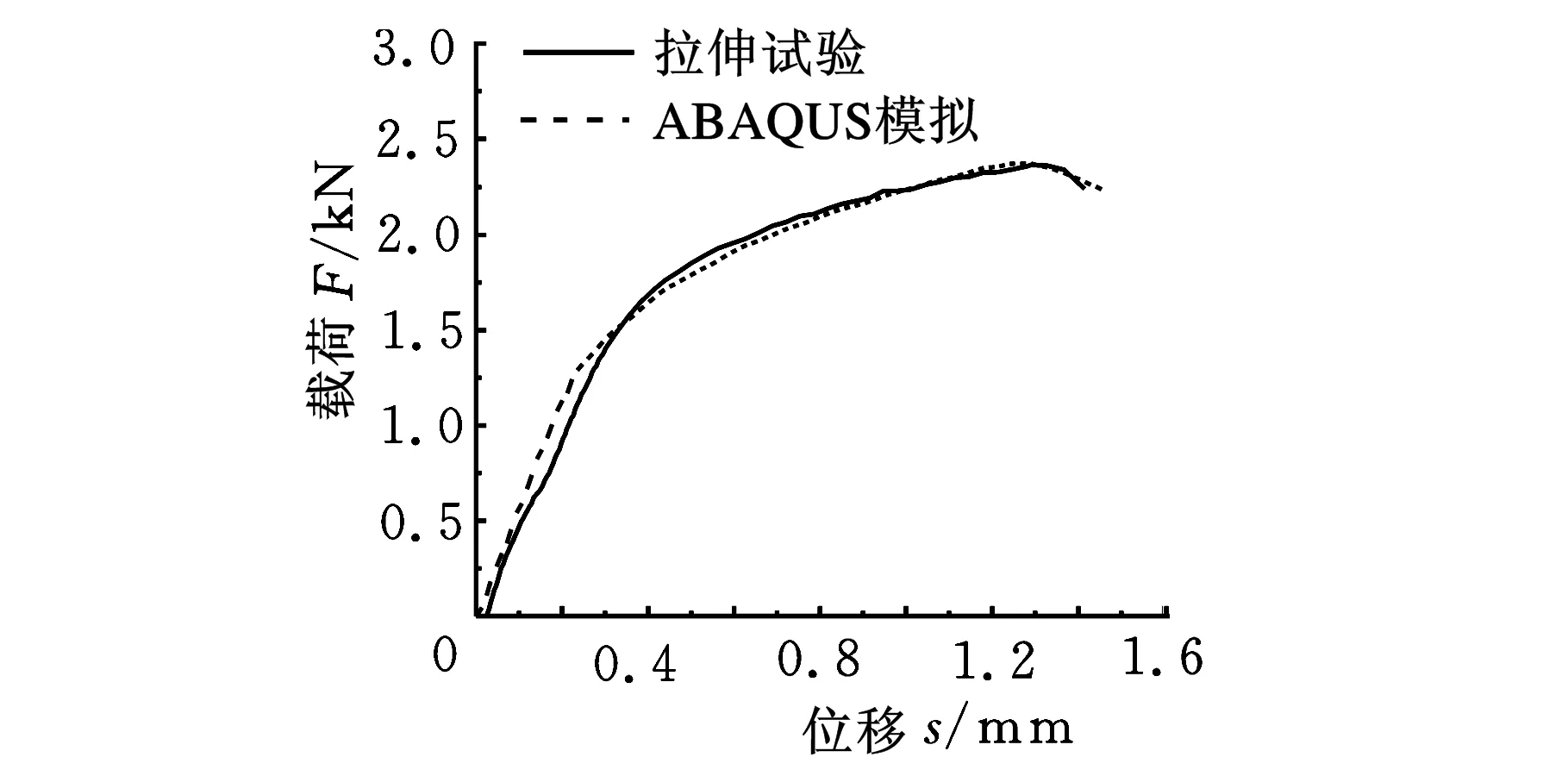
(c)R=4 mm试样图5　试验和有限元计算得到的各试样的载荷-位移曲线

2　断裂应变与应力三轴度的关系

2.1Johnson-Cook断裂模型

Johnson-Cook断裂失效模型是应用较广的失效准则,其表达式为[13]:

2.2数值模拟计算修正

断裂应变计算表达式为

εf=2ln(d0/df)

(1)

式中,d0为试样初始最小截面直径;df为颈缩处最小横截面直径。

根据文献[14],各试样的断裂应变可由试样在起裂时对应的最小截面直径代入式(1)求得。

(2)

式中,σ1、σ2、σ3为三向主应力。

将模拟计算得到的各试样起裂时对应的最小截面直径和各主应力分量的值代入式(1)和式(2)进行计算,从而得到各试样的断裂应变和应力三轴度。表2给出了三组试样在起裂时对应的最小截面直径及计算的断裂应变与应力三轴度的值。用Johnson-Cook断裂失效模型拟合表2中最后两组数据,可确定材料参数D1、D2和D3分别为-0.35、0.619和-0.441。因此，在不考虑应变速率和温度影响时,AZ31B镁合金室温条件下的断裂失效模型为

(3)

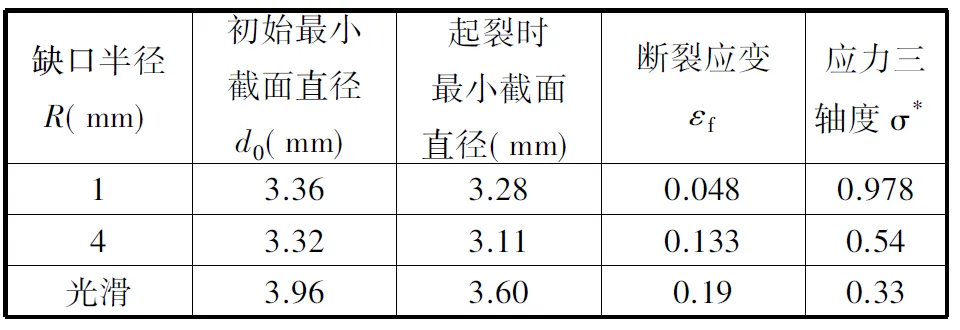
表2　试样的相关参量

图6给出了应力三轴度与断裂应变的关系,可看出,随着应力三轴度的增大,AZ31B镁合金的断裂应变逐渐减小。

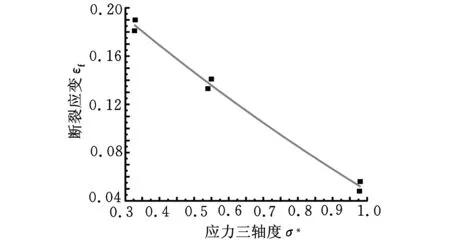
图6　断裂应变与应力三轴度的拟合曲线

3　模型的验证

为了验证得到的AZ31B镁合金断裂应变与应力三轴度的关系模型,将参数D1=-0.35、D2=0.619和D3=-0.441代入ABAQUS中,对缺口半径R=2 mm的圆棒准静态拉伸过程进行仿真模拟,将模拟结果与试验结果进行比较。试样有限元模型如图7a所示,图7b为试样仿真计算后的应力分布图。仿真结果与试验载荷-位移曲线的比较见图8,验证了AZ31B镁合金室温条件下的断裂失效模型的正确性。由图8可知，在载荷达到最大值之前，仿真结果与试验结果十分吻合，当载荷达到最大值后，即试样应力达到其抗拉强度时，材料开始发生颈缩，进而产生裂纹直至失效断裂，此时材料的横截面面积不再均匀变化，试样不再处于单向拉应力状态而是三向应力状态，因此此时通过试验测得的应力应变不是材料真实的应力状态，需要用数值模拟的方法得到材料颈缩后的真实应力状态。

(a)试样有限元模型

(b)试样应力分布图
图7缺口半径R=2 mm试样有限元模型及其应力分布

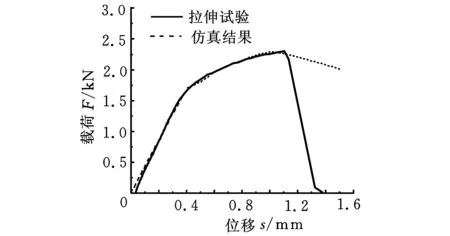
图8　试样有限元仿真结果与试验结果的比较

4　结论

通过准静态拉伸试验,并结合有限元模拟,研究了AZ31B镁合金断裂应变与应力三轴度之间的关系，建立的AZ31B镁合金室温条件下的断裂失效模型为

通过试验和有限元模拟验证了该模型的正确性,说明该模型可以用来描述AZ31B镁合金在不同应力三轴度下的失效关系。研究结果表明：不同应力状态下材料的断裂性能有所不同，随着应力三轴度的减小，AZ31B镁合金的等效弹性模量和等效屈服应力越来越小，断裂应变逐渐增大。

[1]余琨,黎文献,王日初,等.变形镁合金的研究、开发及应用[J].中国有色金属学报,2003,13(2):277-288.Yu Kun,Li Wenxian,Wang Richu,et al.Research，Development and Application of Wrought Magnesium Alloy[J].The Chinese Journal of Nonferrous Metals,2003,13(2):277-288.

[2]Mordike B L,Ebert T.Magnesium : Properties Applications Potential[J].Materials Science and Engineering:A,2001,302(1):37-45.

[3]Gray J E,Luan B.Protective Coatings on Magnesium and Its Alloys a Critical Review[J].Journal of Alloys and Compounds,2002,336(1/2):88-113.

[4]Hancock J W,Brown D K.Onthe Role of Strain and Stress State in Ductile Failure[J].Journal of the Mechanics and Physics of Solids,1983,31(1):1-24.

[5]Mirza M S,Barton D C,Church P.The Effect of Stress Triaxiality and Strain-rate on the Fracture Characteristics of Ductile Metals[J].Journal of Materials Science,1996,31(2):453-461.

[6]Børvik T,Hopperstad O S,Dey S,et al. Strength and Ductility of Weldox 460E Steel at High Strain Rates,Elevated Temperatures and Various Stress Triaxialities[J].Engineering Fracture Mechanics,2005,72(7):1071-1087.

[7]Hopperstad O S,Børvik T,Langseth M,et al.On the Influence of Stress Triaxiality and Strain Rate on the Behaviour of a Structural Steel.Part I.Experiments[J].European Journal of Mechanics A/Solids,2003,22(1):1-13.

[8]Børvik T,Hopperstad O S,Berstad T.On the Influence of Stress Triaxiality and Strain Rate on the Behaviour of a Structural Steel. Part Ⅱ.Numerical Study[J].European Journal of Mechanics A/Solids,2003,22(1):15-32.

[9]陈刚,陈忠富,徐伟芳,等.45钢的J-C损伤失效参量研究[J].爆炸与冲击,2007,27(2):131-135.

Chen Gang,Chen Zhongfu,Xu Weifang,et al.Investigation on the J-C Ductile Fracture Parameters of 45 Steel[J].Explosion and Shock Waves,2007,27(2):131-135.

[10]朱浩，朱亮，陈剑虹. 应力三轴度和应变率对6063 铝合金力学性能的影响及材料表征[J]. 材料科学与工程学报，2007，27(3):358-362.

Zhu Hao,Zhu Liang,Chen Jianhong.Influence of Stress Triaxiality and Strain Rate on the Mechanics Behavior of 6063 Aluminum Alloy and Material Characterization[J].Journal of Materials Science & Engineering,2007,27(3):358-362.

[11]张伟,肖新科,魏刚.7A04铝合金的本构关系和失效模型[J].爆炸与冲击,2011,31(1):81-87.

Zhang Wei,Xiao Xinke,Wei Gang.Constitutive Relation and Fracture Model of 7A04 Aluminum Alloy[J].Explosion and Shock Waves,2011,31(1):81-87.

[12]张伟,魏刚,肖新科.2A12 铝合金本构关系和失效模型[J].兵工学报,2013,34(3):276-282,Zhang Wei,Wei Gang,Xiao Xinke.Constitutive Relation and Fracture Criterion of 2A12 Aluminum Alloy[J].Acta Armamentarii,2013,34(3):276-282.

[13]Johnson G R,Cook W H.Fracture Characteristics of Three Metals Subjected to Various Strains,Strain Rates,Temperatures and Pressures[J].Engineering Fracture Mechanics,1985,21(1):31-48.

[14]谢凡,张涛,陈继恩,等.应力三轴度的有限元计算修正[J].爆炸与冲击,2012,32(1):8-14.

Xie Fan,Zhang Tao,Chen Ji’en,et al.Updating of the Stress Triaxiality by Finite Element Analysis[J].Explosion and Shock Waves,2012,32(1):8-14.

(编辑苏卫国)

Research on Relationship of AZ31B Magnesium Alloy Fracture Strain and Stress Triaxiality

Zhou MengchengFeng FeiHu JianhuaLei YuHe PengHuang ShangyuZou Fangli

Wuhan University of Technology,Wuhan,430070

Series of quasi-static tensile tests were conducted on smooth and notched round rod made of AZ31B magnesium alloy.ABAQUS software was used to simulate the tensile process of each sample.Part material constants of Johnson-Cook fracture failure model were fitted out,and the relational model between fracture strain and stress triaxiality of AZ31B magnesium alloy were established.Inputing the fracture failure model into ABAQUS for simulation,the simulation results and experimental results are basically consistent,thus the correctness of the fracture failure model was verified.

AZ31B magnesium alloy;quasi-static tensile experiment;Johnson-Cook failure model;finite element simulation

2013-11-08

国家自然科学基金资助项目(50875192，51205298)；材料成形与模具技术国家重点实验开放基金资助项目(2010-P08)

TG146.2DOI：10.3969/j.issn.1004-132X.2015.05.022

周梦成,男,1991年生。武汉理工大学材料科学与工程学院博士研究生。主要研究方向为材料成形新技术。冯飞，男，1986年生。武汉理工大学材料科学与工程学院博士研究生。胡建华,男,1966年生。武汉理工大学材料科学与工程学院副教授。雷雨,男,1989年生。武汉理工大学材料科学与工程学院博士研究生。何鹏,男,1986年生。武汉理工大学材料科学与工程学院博士研究生。黄尚宇(通信作者),男,1963年生。武汉理工大学材料科学与工程学院教授、博士研究生导师。邹方利,女,1979年生。武汉理工大学材料科学与工程学院博士研究生,武汉工程大学机电学院讲师。