机电集成电磁蜗杆传动在系统参数激励下的稳定性分析

关雪梅　郝秀红

燕山大学，秦皇岛，066004

机电集成电磁蜗杆传动在系统参数激励下的稳定性分析

关雪梅郝秀红

燕山大学，秦皇岛，066004

考虑到机电集成电磁蜗杆传动系统的参数振动由外界的激励产生，通过系统内参数的周期性改变间接地实现，推导出描述参数振动的数学模型为周期变系数的常微分方程；通过对系统转动惯量波动进行分析可知系统是稳定的；利用系统参数刚度矩阵和小参数导出系统微分方程，将其正则化得到系统微分方程的通解，进而得到判断因子，从而确定系统的动力稳定状态，并用具体算例进行了验证。

机电集成；电磁蜗杆传动；转动惯量；啮合刚度；稳定性分析

0　引言

随着现代科学技术的不断发展，多学科之间的交叉与渗透越来越深入，实现机、电与控制有机结合的广义复合传动机构已成为机械科学领域的国际性前沿课题[1-2]。本文给出了一种机电集成电磁蜗杆传动机构，该机构是电磁驱动技术与传统蜗杆传动技术相结合的一种新型传动形式，是一种有源、无接触的广义复合运动，它集蜗杆传动和电动机功能于一体，进一步增强了蜗轮蜗杆传动的功能，具有实际应用价值，可广泛应用于航空航天、军事、车辆等要求结构紧凑的领域。

机电集成电磁蜗杆传动机构的驱动特点是蜗杆产生的环面旋转磁场驱动以多个永磁体为轮齿的蜗轮转动，从而带动支撑蜗轮的输出轴转动而实现低速大扭矩的动力输出。参数振动由外界的激励产生，但激励不是以外力形式施加于系统，而是通过系统内参数的周期性改变间接地实现。由于参数具有时变性，所以参数振动系统为非自治系统。描述参数振动的数学模型为周期变系数的常微分方程，对参数振动的研究归结于对时变系统常微分方程组零解稳定性的研究。

1　转动惯量波动分析

机电集成电磁蜗杆传动系统结构如图1所示，该机构由中心环形蜗杆及装有永磁齿的蜗轮组成。中心环面蜗杆上均匀分布着螺旋槽，槽内安放电磁线圈。当线圈内通以三相交流电时产生交变磁场，磁场力驱动蜗轮转动，输出转矩。传动系统中，蜗轮围绕其支撑轴旋转，由于存在安装、制造误差，蜗轮质心不可能恰好位于支撑轴轴心位置，这导致了蜗轮回转中心会发生周期性波动，从而使得其转动惯量产生周期性波动，波动幅值ΔMp与蜗轮质量以及蜗轮偏心距有关。波动频率ωr与蜗轮回转速度有关。图1中，φv代表蜗杆的齿冠角。

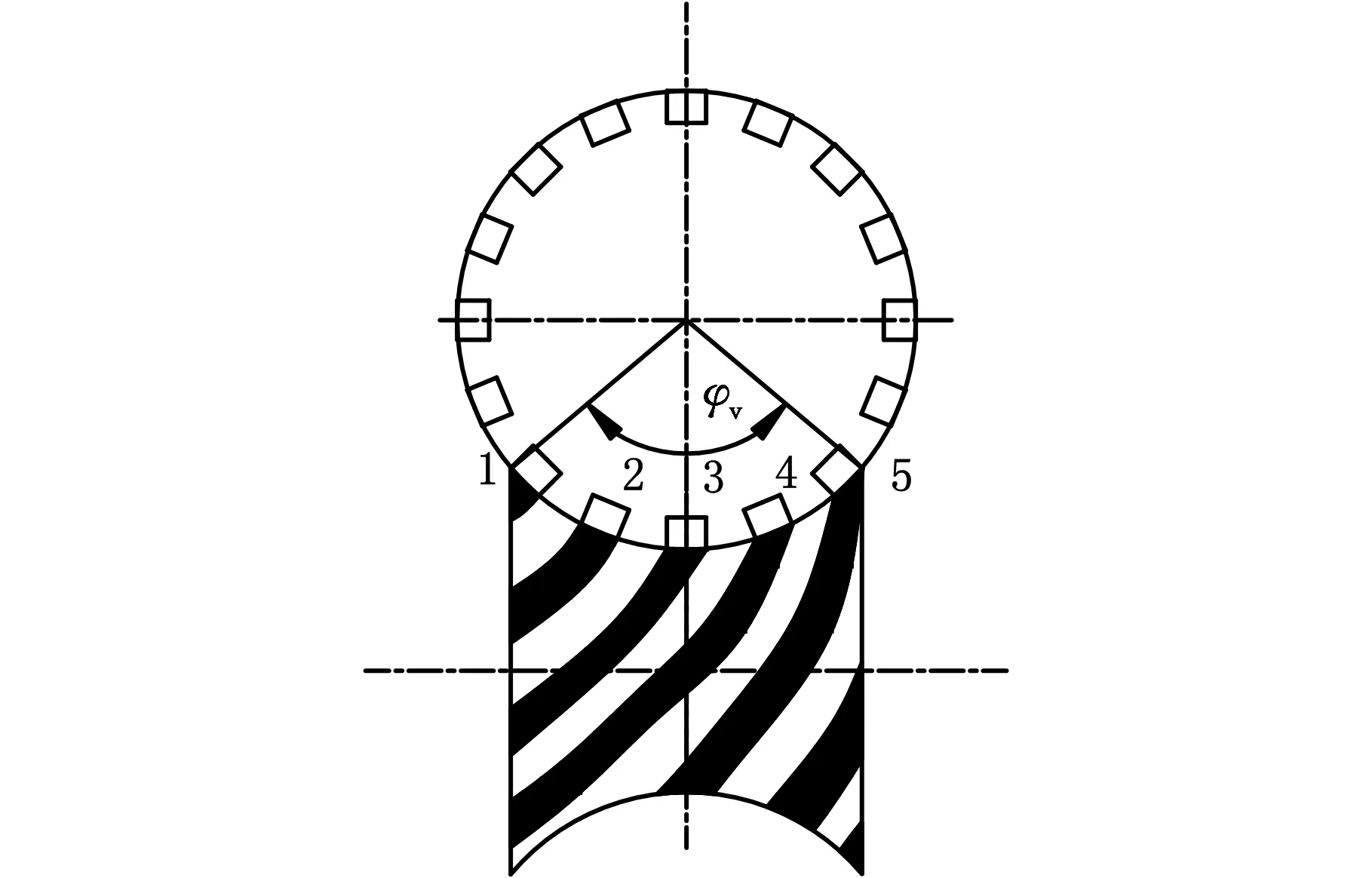
图1　电磁蜗杆传动系统结构示意图

设蜗轮转动惯量呈正弦规律波动，则当ΔM=ΔMpcosωrt时，系统无阻尼自由振动微分方程为[3-4]

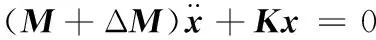
(1)

式中，K为系统刚度矩阵；M为质量矩阵；x为位移矩阵。

由于转动惯量波动幅值很小，故可将式(1)正则化后写为

(2)

MN=diag(MN1,1,MN2,2,…,MNi,i,…,MN3m+1,3m+1)

ΔMN=cosωrt·

diag(ΔMN1,1,ΔMN2,2,…,ΔMNi,i,…,ΔMN3m+1,3m+1)

由ΔMN的形式可知，前三项旋转模态所对应的元素不为零，其他位置元素为零，即蜗轮转动惯量的波动对蜗轮及蜗杆模态没有影响[5-6]，即

(3)

对式(3)进行简化、变形和展开处理可得

(4)

设

(5)

对式(4)进一步化简可得

(6)

式(6)为比较典型的拟周期马蒂厄方程，式(6)的通式可写为

(7)

当ε=0时，为确保线性保守系统的周期解等于π或2π，必须有δ=n2(n=0,1,…)，分别对应于线性无关的特解sinnt和cosnt，除n=0时的周期解为常数值以外，n为偶数时周期为π，n为奇数时周期为2π。利用林滋泰德-庞加莱摄动法，将式(7)的解x(t)和参数δ都展开成ε的幂级数，经过求解可得[7]

(8)

进一步计算可得n取不同值时δ的表达式。

由以上讨论可得到如下结论：当ωr≈ωi时,δ≈4，在δ>4+11ε2/48+…,δ<4-7ε2/48+…范围内系统是稳定的。当ωr≈2ωi时，δ≈1，在δ>1+ε/2-ε2/32+…,δ<1-ε/2-ε2/32+…范围内系统是稳定的。

当ωr≈2ωi/3时，n≈3，此时的稳定边界线近似为一条线，所以系统始终是稳定的，系统稳定图见图2。

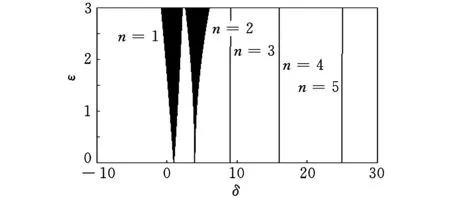
图2　系统稳定图

由上文分析可知，当n逐渐增大时，转动惯量参数激励对系统影响的稳定区域越来越大，转动惯量参数激励频率越低，系统越稳定。当n≥3时，系统稳定边界线近似是一条直线，此时系统总是稳定的。当n>7(ωr<75 rad/s)时，系统总是处于稳定的状态。

ΔMp是转子转动惯量波动幅值，其大小决定了小参数ε的大小。所以考察小参数ε对于系统稳定性的影响，即可以反映惯量波动幅值ΔMp的影响，由图2可知当小参数ε增大时，不稳定区域将会增大，系统稳定性变差,当小参数ε减小时，不稳定区域将会减小，系统稳定性变好。

根据以上理论分析，下面计算当转子转动惯量激励频率ωr≈2ω1时系统的稳定性。当ωr为300 rad/s、600 rad/s、1120 rad/s，ΔMNi,i/MNi,i=0.1时，系统3阶旋转模态固有圆频率分别为295 rad/s、518.5 rad/s、1125.3 rad/s。将上面数据代入式(5)得参数值如表1所示。将表1的数据代入相应公式可得当ωr为300 rad/s、600 rad/s、1120 rad/s时，系统稳定状态值在不同固有圆频率范围内的取值，见表2。

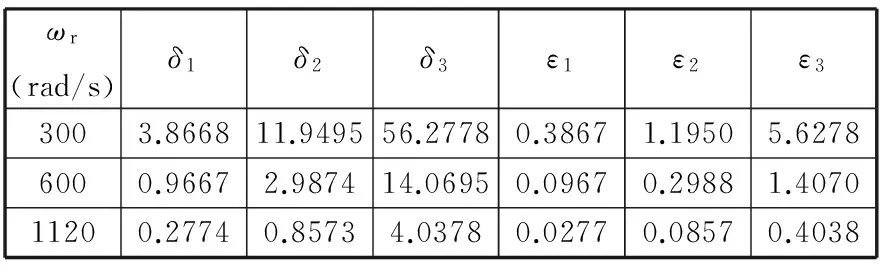
表1　算例系统方程的参数δ和ε

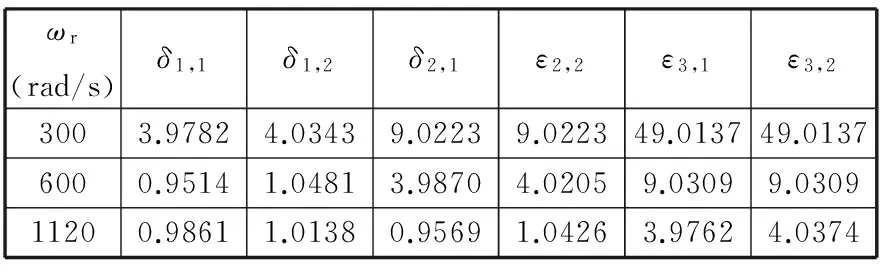
表2　算例系统稳定性参数δi,j和εi,j

由表1和表2各参数可知，当ωr=2ω1时系统各频率对应的状态点均处于稳定区域内。系统的稳定图见图3，可以看出此时系统是稳定的。

2　啮合刚度波动的稳定性分析

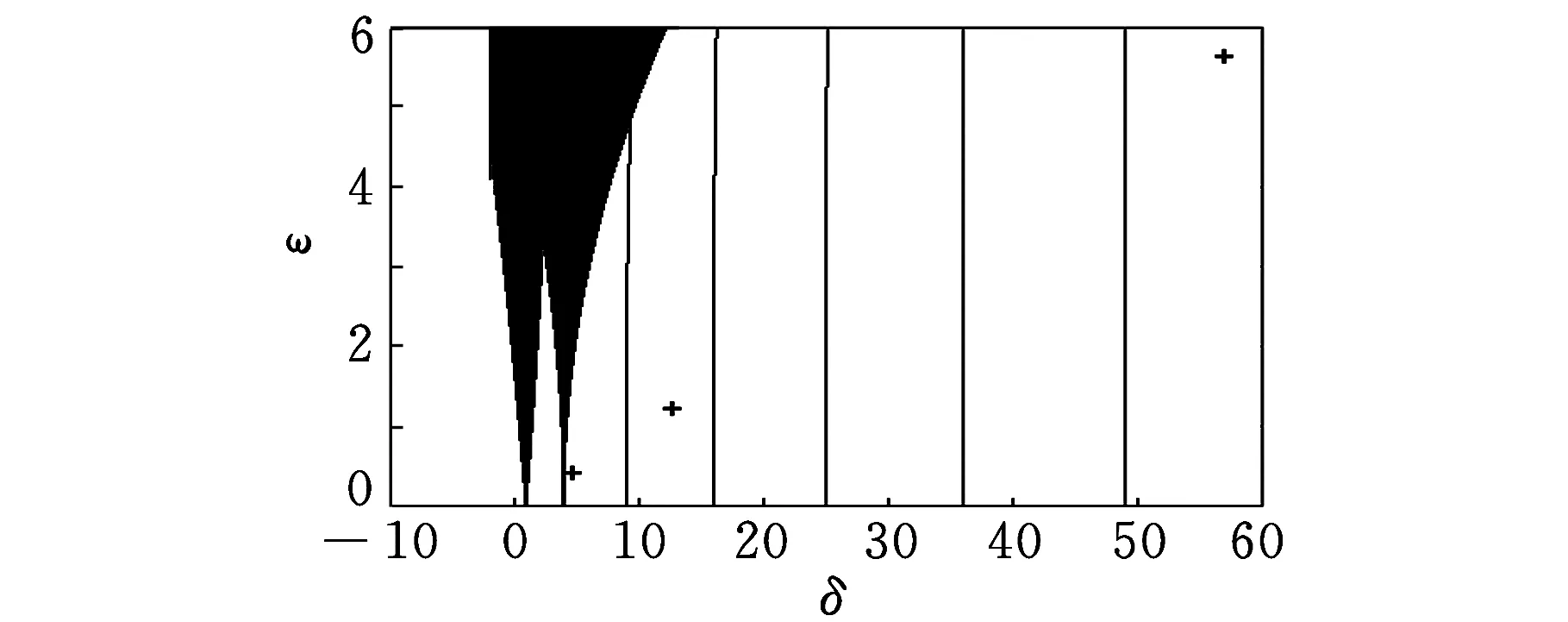
(a)ωr=300 rad/s

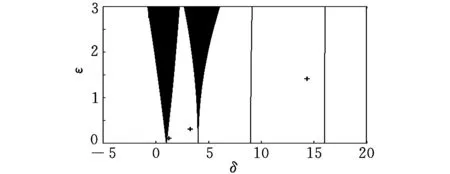
(b)ωr=600 rad/s

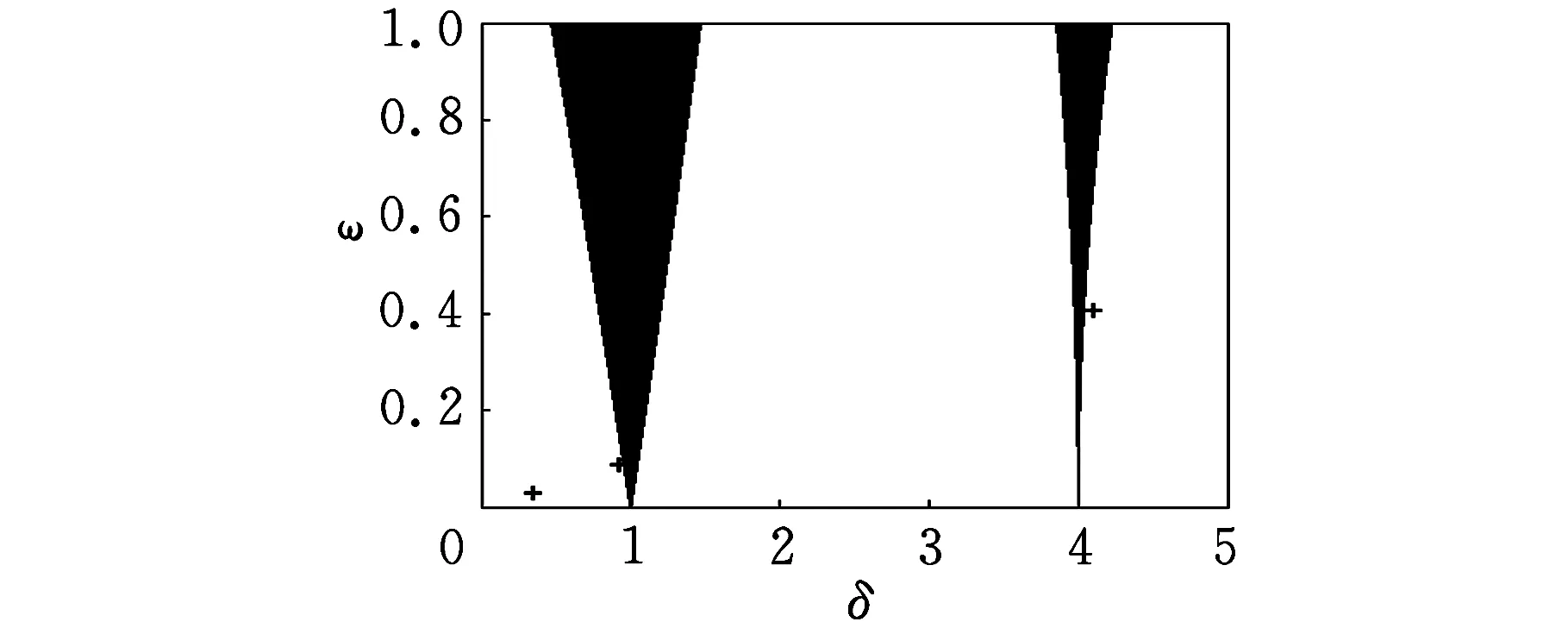
(c)ωr=1120 rad/s图3　转子惯量波动激励下机械系统稳定图

电磁蜗杆传动系统中蜗轮运转时与蜗杆间的啮合齿对数呈周期性变化，蜗轮其他方向的支撑刚度不发生变化，同时由于安放电磁线圈的蜗杆被约束，不发生转动，因此除蜗轮扭转振动外，本文不考虑蜗杆及蜗轮其他方向的振动情况，且假设蜗杆与蜗轮间的包角为90°，蜗轮与蜗杆间啮合轮齿对数的变化如图4所示[8]，其中，k为啮合刚度，θ为包角。

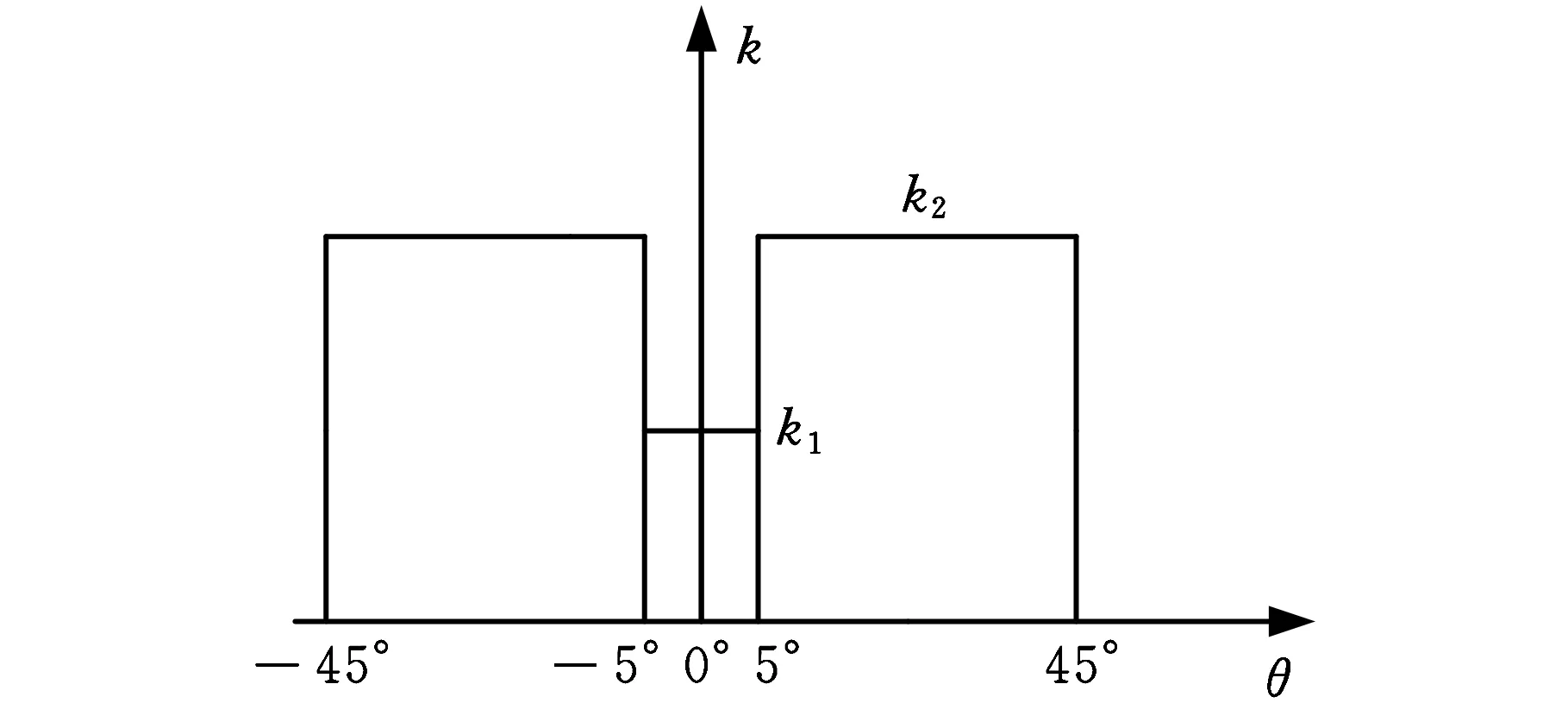
图4　蜗轮与蜗杆间啮合轮齿对数的变化图

由图4可知，蜗轮与蜗杆啮合刚度呈方波形式变化，啮合刚度函数可表示为如下的方波形式:

(9)

当蜗轮旋转角-5°<θp≤5°时，蜗轮扭转振动运动微分方程为

(10)

式中，Mp为系统主质量矩阵。

将式(10)整理可得

(11)

式(11)的通解为

u1=Asinω1t+Bcosω1t

(12)

当蜗轮旋转角5°≤θp≤40°或-40°≤θp≤-5°时，蜗轮扭转振动运动微分方程为

(13)

将式(13)整理可得

(14)

式中，γ为蜗轮与蜗杆接触点的导程角。

式(14)的通解为

u2=Csinω2t+Dcosω2t

(15)

积分常数A、B、C、D满足解的连续性及正规解条件：

(16)

将式(12)和式(15)代入式(16)可得

(17)

从A、B、C、D的非零解条件导出σ应满足的本征方程如下：

σ2-2aσ+1=0

(18)

从式(18)解出本征值为

下面分几种情况进行讨论：

(1)当|a|>1时，σ1、σ2中肯定有一个根的值大于1，其对应的解是无界的，且系统零解不稳定。

(2)当|a|<1时，σ1、σ2为共轭复根，由于σ1·σ2=1，因此共轭复根的模肯定等于1，方程的基本解是有界的，且系统零解稳定。

(3)当|a|=1时，σ1=σ2=±1为重根，其解是以T或2T为周期的周期解，是介于稳定与不稳定之间的临界情形。

代入样机系统参数就可得到刚度呈方波变化的系统微分方程，将其正则化得到如式(11)和式(16)所示的系统微分方程的通解，代入式(18)进而得判断因子|a|，从而确定系统的动力稳定状态[9]。

改变蜗轮与蜗杆的包角，蜗轮与蜗杆啮合过程中啮合齿对数及啮合时间会发生变化。假设蜗轮与蜗杆之间的包角为φv。蜗轮上安装有z个齿，系统设计需要φv>360°/z，这里先假定φv<720°/z，即啮合过程中是单对齿与双对齿的啮合，则传动过程中啮合刚度变化情况为

(19)

由上述分析可知，式(11)和式(14)中积分常数A、B、C、D满足解的连续性及正规解条件，即

(20)

将式(12)和式(15)代入式(20)可得

从A、B、C、D的非零解条件导出σ应满足的本征方程如下：

σ2-2aσ+1=0

以蜗轮永磁体个数取8为例，改变包角φv大小，此时判断因子a的变化情况如图5所示。

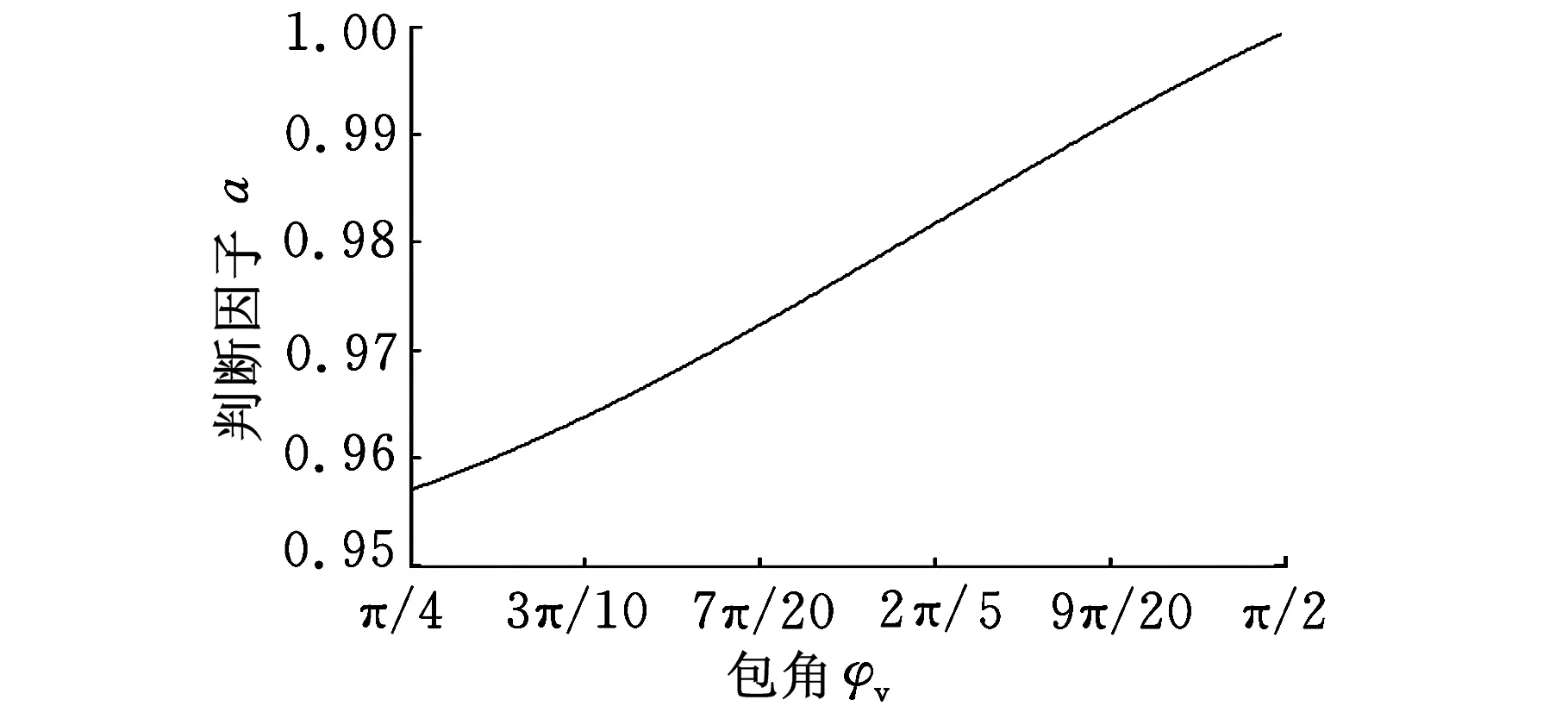
(a)z=6

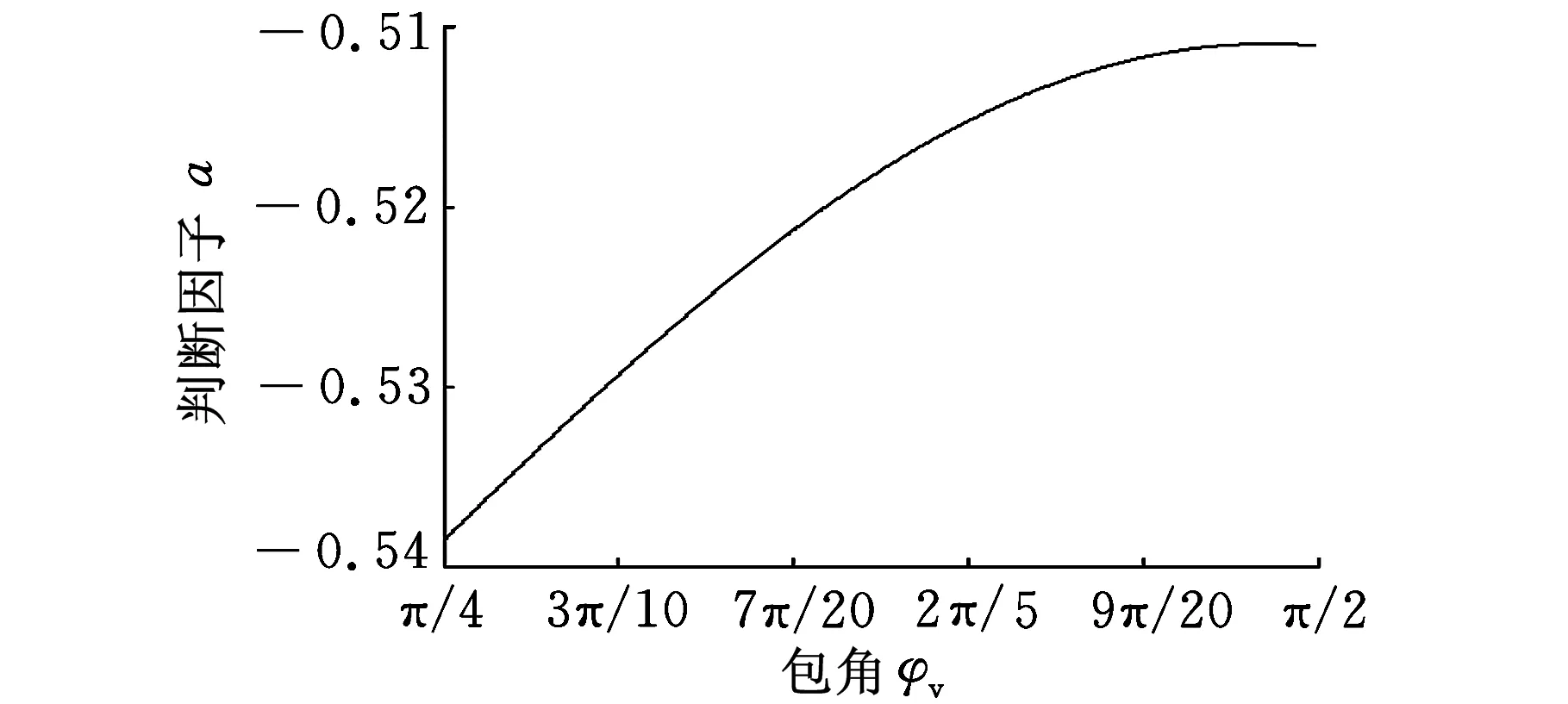
(b)z=8

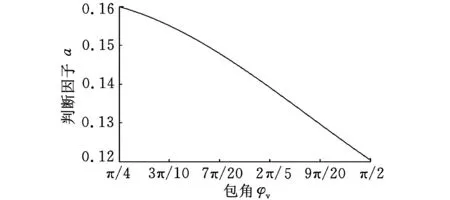
(c)z=10

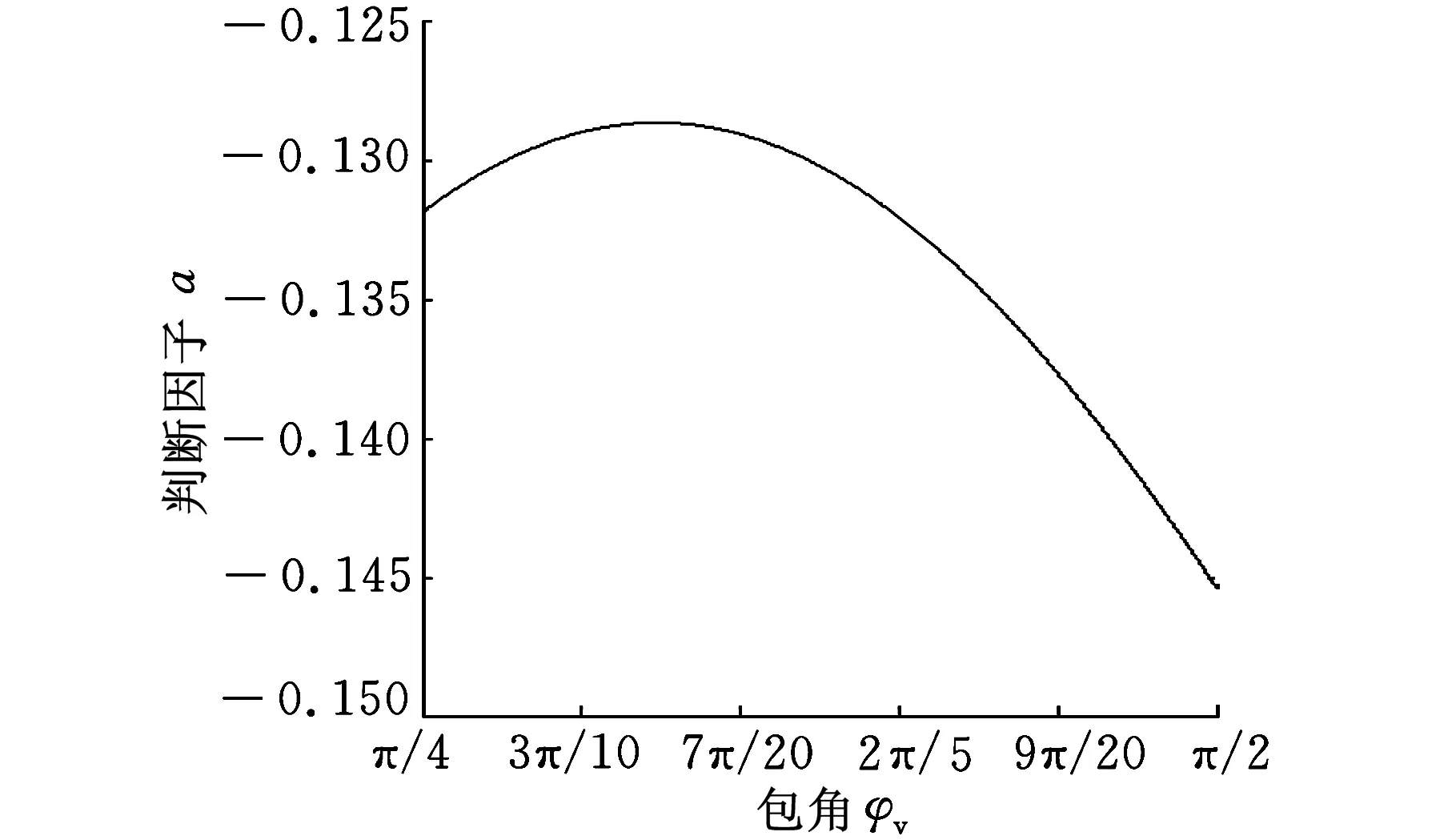
(d)z=12图5　判断因子a的变化图

由图5可知，当蜗轮上安装有6、8、10、12个磁极，且蜗轮与蜗杆间的包角在π/4到π/2之间变化时，判断因子a的绝对值小于1，因此系统始终是稳定的。其中，当蜗轮齿数为10时判断因子a的绝对值较大，接近于1，其他蜗轮齿数分别为6、8、12时判断因子a的值较小。

判断因子a的绝对值小于1时，其值越小，系统稳定性越好，相反则系统稳定性越差。根据上述推导的公式及其变化规律，可进行系统稳定性判断和优化参数的选取。

3　结语

机电集成电磁蜗杆传动系统内参数的周期性改变是由外界的激励产生的，描述参数振动的数学模型为周期变系数的常微分方程，对参数振动的研究归结于对时变系统常微分方程组零解稳定性的研究。通过对系统转动惯量波动分析可知系统是稳定的；利用系统参数刚度矩阵和小参数导出系统微分方程，将其正则化得到系统微分方程的通解，进而得到判断因子，从而确定系统的动力稳定状态，并用具体算例进行了验证。

[1]秦大同.机械传动科学技术的发展历史与研究进展[J].机械工程学报, 2003,39(12):37-44.

QinDatong.DevelopmentHistoryandResearchProgressofMechanicalDriveScienceandTechnology[J].ChineseJournalofMechanicalEngineering,2003,39(12):37-44.

[2]刘冰.浅谈光机电一体化技术的发展方向[J].论坛,2010(12):33-134.

LiuBing.IntroductiontoOpticalIntegrationTechnologyDevelopmentDirection[J].Forum, 2010(12):133-134.

[3]刘金生.机电耦合系统的动力学特性研究[D].沈阳:东北大学, 2006.

[4]YoussefKH,KamalAH.AnalysisoftheElectromechanicalVibrationsinInductionMotorDrivesDuetotheImperfectionsoftheMechanicalTransmissionSystem[J].MathematicsandComputersinSimulation，2003，63(17)：421-433.

[5]XuLizhong,HaoXiuhong.DynamicModelforElectromechanicalIntegratingToroidalDrive[J].InternationalJournalofAppliedElectromagneticsandMechanics. 2005，22(3/4)：199-211.

[6]郝秀红,许立忠. 机电集成超环面传动啮合参数激励下的稳定性分析[J].中国机械工程,2007,18(24):2947-2950.

HaoXiuhong,XuLizhong.StabilityAnalysisforElectromechanicalIntegratingofToroidalDriveundertheParameterExcitationofMesh-stiffness[J].ChinaMechanicalEngineering, 2007,18(24):2947-2950.

[7]许立忠,郝秀红.机电集成超环面行星蜗杆传动机电耦合动力学[M]. 北京:兵器工业出版社,2010.

[8]AhmetK.FreeTorsionalVibrationCharacteristicsofCompoundPlanetaryGearSets[J].MechanismandMachineTheory, 2004,39:953-971.

[9]郝秀红,许立忠. 机电集成超环面传动系统三重内共振[J].中国机械工程,2012,23(24):2955-2961.

HaoXiuhong,XuLizhong.ThreeDOFInternalResonancesofElectromechanicalIntegratingToroidalDriveSystem[J].ChinaMechanicalEngineering, 2012,23(24):2955-2961.

(编辑王艳丽)

Stability Analysis for Electromechanical Integrated Electromagnetic Worm Drive under Parameter Excitation

Guan XuemeiHao Xiuhong

Yanshan University，Qinhuangdao，Hebei，066004

The parametric vibration of electromechanical integrated electromagnetic worm drive was caused by external excitation,and indirectly realized through the system internal parameters of periodic changes. The mathematical model describing parameter vibration was an ordinary differential equation of periodic variable coefficient. The system was stable through the rotational inertia fluctuation analysis.The system differential equation was derived by using system parameters of stiffness matrix and a small parameter,and the general solution was obtained by regularization,the determine factors were obtained, the dynamic stability status of the system was confirmed and verified by an example.

electromechanical integration; electromagnetism worm drive; rotational inertia; meshing stiffness; stability analysis

2013-07-25

国家自然科学基金资助项目(51075350)；秦皇岛市科技支撑计划资助项目(2012021A055)

TH113.1DOI：10.3969/j.issn.1004-132X.2015.05.017

关雪梅，女，1971年生。燕山大学车辆与能源学院高级工程师、博士。研究方向为磁力机械。发表论文6篇。郝秀红，女，1979年生。燕山大学机械工程学院副教授、博士。