复杂环境下的装配路径求解与优化

姜　康　胡　龙

合肥工业大学，合肥，230601

复杂环境下的装配路径求解与优化

姜康胡龙

合肥工业大学，合肥，230601

针对三维复杂环境下的装配路径规划问题，运用栅格法建立了规划空间模型，基于蚁群算法求解出了一条避开障碍物的初始路径；对求解得到的装配初始路径，提出采用二分法插值优化方法缩短装配路径长度，在规划过程中采用目标零件与障碍物的轴向包围盒进行避障。对装配路径的求解及优化进行了实例测试，获得了一条无碰撞的最短的平滑路径，验证了算法的有效性和可行性。

装配路径规划；规划空间；蚁群算法；二分法插值优化

0　引言

良好的装配工艺规划可以提高效率和质量，缩短加工时间，并降低整个产品制造过程中的成本，因此，对装配路径规划进行研究十分必要[1]。

装配路径规划是指在有障碍物的工作环境下，寻找从起始位姿到终止位姿的一系列点或曲线，旨在避开空间障碍并提高装配效率[2]。装配路径的求解是路径规划环节的核心部分，路径的求解一方面是为了避障或满足作业需要，另一方面用于验证产品设计和装配序列规划是否合理[3]。

随着产品日趋复杂化、大型化、精密化，装配路径的求解也愈加复杂，国内外学者在装配路径求解方面取得了大量的研究成果：如VMap法[4]、A*搜索算法[5]、视点跟随法[6]、力反馈引导法[7]、人工势场法[8]、遗传算法[9]、RRT算法[10-11]等。这些算法求解的是二维环境条件下或较简单的三维环境下的装配路径，没有考虑产品在多障碍物环境下的路径规划问题。由于复杂环境下空间规模大、多约束、非线性，对路径的求解必须进行大量的碰撞检测，所以算法效率低，实际工程应用缺乏。

蚁群算法由Dorigo[12]提出，近年来已被广泛应用于路径规划问题、旅行商问题、生产调度问题等。蚁群算法具有群体智能等优势，在路径规划上具有很大的潜力，文献[13]提出了基于可视图法与蚁群算法的装配路径规划方法，该算法解决的是二维环境条件下简单的装配路径求解问题，至于在三维环境条件下的效果还有待验证；文献[14]将蚁群算法用于求解装配序列规划，文献[15]基于改进的蚁群算法和分布式局部导航对多机器人系统的路径进行规划，但只是将蚁群算法用于求解较简单环境下的路径规划。

本文基于蚁群算法对三维复杂环境下的装配路径规划进行了详细的分析，并给出了实例验证，最后对求解的初始路径进行了优化。

1　装配路径规划问题描述

1.1路径规划概述

路径规划是指在有障碍物的工作环境中寻找一条从起点到终点、无碰撞地绕过所有障碍物的运动路径的过程。装配路径规划的总体思路如下：①从产品的CAD模型中抽象出三维规划空间；②应用路径搜索算法求解出一条避障且路径最短的初始路径；③优化初始路径，得到最终装配路径。对装配路径规划的描述如图1所示。

图1　装配路径规划描述

图1中环境空间是一个包含机械零部件、工装夹具、障碍物等信息的无限大的空间，而目标零件从起始点到目标点的路径是一个有限的空间，所以需要对目标零件确定一个有限的规划空间。在规划空间中分布着位置与形状已知的障碍物(图1中的1、2、3)，在路径规划时，将障碍物尺寸根据目标零件的尺寸及运行安全性要求进行相应“膨化”处理，使“膨化”后的障碍物边界为安全区域，这样目标零件就可以看作一个质点。目标零件的路径path由目标零件从起始点S到目标点G绕过障碍物的有限个路径点组成，即

path={S,P1,P2,…,Pi,…,G}i=1,2,…

1.2规划空间建模

装配路径规划首先需要从产品的CAD模型中抽象出三维空间模型。其方法为：以规划空间左下角的顶点作为坐标原点O建立空间直角坐标系；采用栅格法对规划空间进行划分(图2)：设该规划空间由(Xmin,Xmax,Ymin,Ymax,Zmin,Zmax)确定，先沿X轴方向进行Nx等分，再沿Y轴方向进行Ny等分，最后沿Z轴方向进行Nz等分，则沿X、Y、Z轴方向的像素单位分别为a、b、c，其关系如下式所示：

(1)

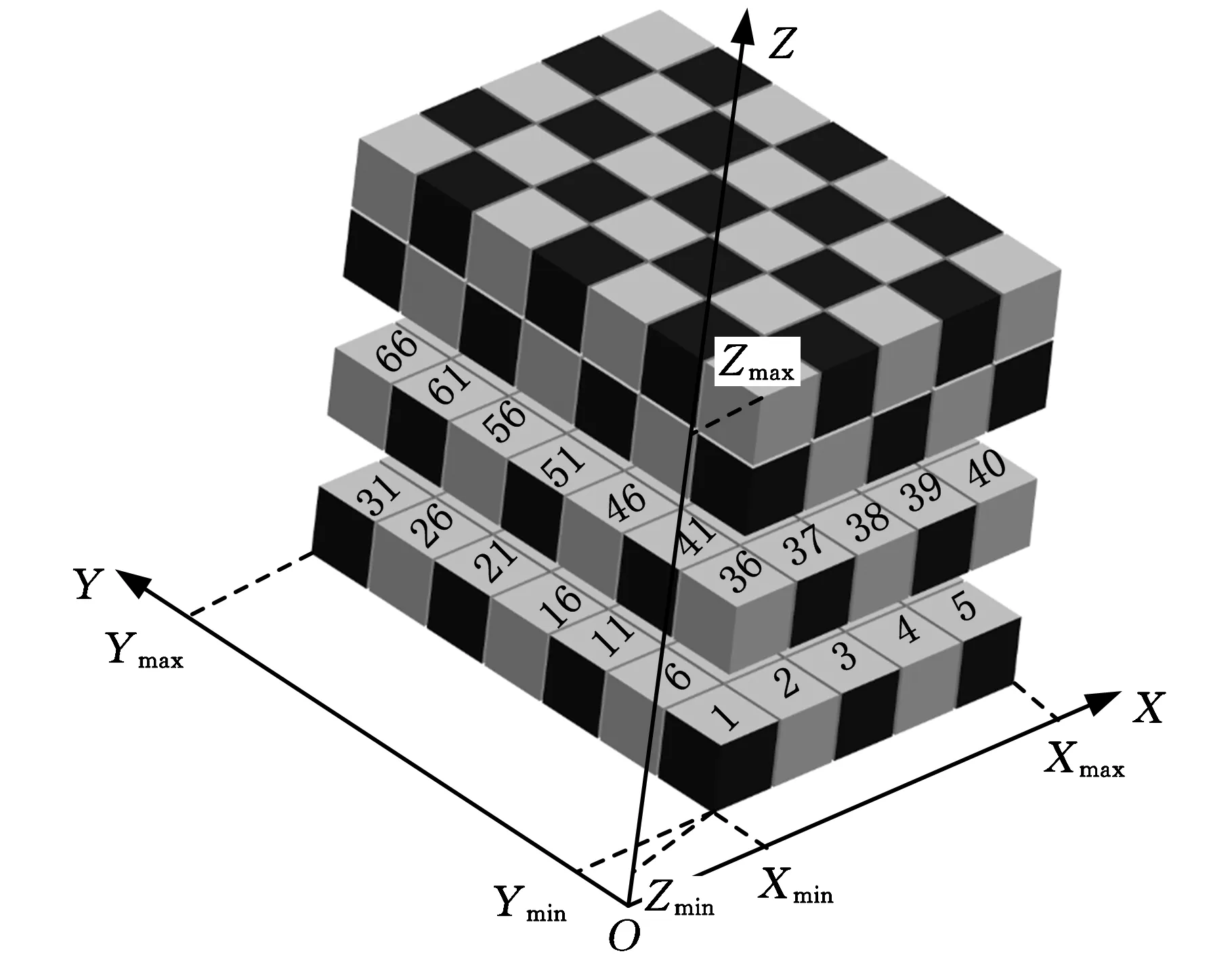
图2　规划空间建模

如此整个规划空间就离散化为一个小长方体集合，集合中的每个元素对应着相应的序号Ri和坐标(Xi,Yi,Zi)，而且序号与坐标一一对应，则可得关系式如下：

(2)

其中，坐标(Xi,Yi,Zi)取长方体栅格的质心处坐标；mod为取余运算，floor为返回小于或等于指定表达式的最大整数函数；ceil为返回大于或者等于指定表达式的最小整数函数。

图2中，Nx=5，Ny=7，Nz=4，第1个小长方体序号R1=1，位置坐标(X1,Y2,Z1)=(0.5a,0.5b,0.5c)；第36个小长方体序号R36=36，位置坐标(X36,Y36,Z36)=(0.5a,0.5b,1.5c)，…，其余以此类推。

2　基于蚁群算法的装配路径规划

2.1装配路径规划分析

装配路径规划要求找到一条从起点到终点的绕过有限个障碍物的最佳路径，为求解装配路径规划问题，首先需要构造规划空间，按1.2节的方法建立规划空间模型。建立规划空间时，像素a、b、c的值需根据障碍物的疏密程度及目标零件的尺寸等进行合理设置。像素小，环境信息描述得更精确，但会加大计算量；像素大，环境信息描述得不够精确，影响路径规划的效果。

在路径规划过程中，蚂蚁只能从当前栅格向其邻域栅格运动，如图3所示。当前栅格Ri的邻域neighbor(Ri)指的是以当前栅格为中心的立方体。图3中除Ri共26个元素，其中N1=NxNy。Ri的邻域为

neighbor(Ri)={Ri-1,Ri+1,Ri+Nx,Ri+Nx-1,

Ri+Nx+1,Ri-Nx,Ri-Nx-1,Ri-Nx+1,Ri+N1,Ri+N1-1,Ri+N1+1,Ri+N1+Nx,Ri+N1+Nx-1,Ri+N1+Nx+1,Ri+N1-Nx,Ri+N1-Nx-1,

Ri+N1-Nx+1,Ri-N1,Ri-N1-1,Ri-N1+1,

Ri-N1+Nx,Ri-N1+Nx-1,Ri-N1+Nx+1,Ri-N1-Nx,Ri-N1-Nx-1,Ri-N1-Nx+1}

栅格Ri、Rj间的距离指两栅格的连线长度，即

(3)

图3　当前栅格的邻域

在用蚁群算法求解路径规划时，由于下一个可以前往的节点可能在障碍物中，所以，当前栅格Ri的可行邻域必须要去除落在障碍物中的栅格及禁忌表中已经过的栅格，即

allow(Ri)=neighbor(Ri)-tabu(m)-obs

(4)

其中，allow(Ri)表示Ri的可行邻域，tabu(m)表示第m只蚂蚁的禁忌表，obs表示障碍栅格集，“-”为集合的差集运算。

在装配路径规划过程中，为了能够尽快找到一条最优路径，需要对已装配的装配体进行简化处理，如用轴向包围盒包围复杂的形状等，并将障碍物尺寸按目标零件尺寸的一半及安全指标同向扩展，进行膨化处理，对环境中存在的障碍物，如果不满一个栅格按一个栅格处理。目标零件的位姿在装配运动过程中保持不变。

2.2路径规划计算步骤

基于蚁群算法的装配路径规划的具体计算步骤如下。

(1)初始化参数。

(2)将循环次数k←k+1。

(3)将蚂蚁数目m←m+1。

(4)创建路径表path、禁忌表tabu，将起点S添加到path、tabu中。

(5)

其中，τij(t)为信息素的浓度，ηij(t)为启发式信息，α、β分别为τij(t)、ηij(t)的权重参数。为了能够尽快找到一条最优路径，ηij(t)取为当前栅格至目标点距离的倒数；allowk表示蚂蚁k下一步允许选择的可行邻域。

(6)若所有蚂蚁都遍历完，则更新信息量；否则跳转到步骤(3)。

(7)重复步骤(2)～步骤(6)，直至达到最大循环次数K，则循环结束并输出结果。

3　基于二分法的装配路径插值优化方法

3.1二分法插值优化方法

由于蚁群算法在选择路径时会走过一些多余的栅格，使得由一系列离散点连接成的装配初始路径不够平滑，同时栅格像素的大小也会增加一些不必要的路径长度，为提高算法的可用性，本文对装配初始路径形成的离散点进行插值优化，尽量使规划的路径更加符合实际。

文献[16]提出一种基于分段线性拟合的装配路径优化技术，但该算法会产生路径冗余中间点。为此，本文提出二分法插值优化方法对规划出的装配初始路径进行优化。

图4　二分法插值优化描述

二分法插值优化描述如图4所示，其中①为初始路径，②为优化后的路径。①中的点从P(1)→P(2)→P(3)→P(4)，起始点为P(1)，若连接点P(1)→P(2)的路径不与障碍物相碰，连接点P(1)→P(3)的路径与障碍物相碰，则查找范围为P(2)→P(3)，再找线段P(2)→P(3)上的一点Q，使得连接点P(1)→Q的路径不与障碍物相碰。3.2路径优化的计算流程

图5为二分法插值优化计算流程，其中P为初始路径中目标零件的位置，L为优化后路径的长度，path记录优化过程中目标零件的位置。

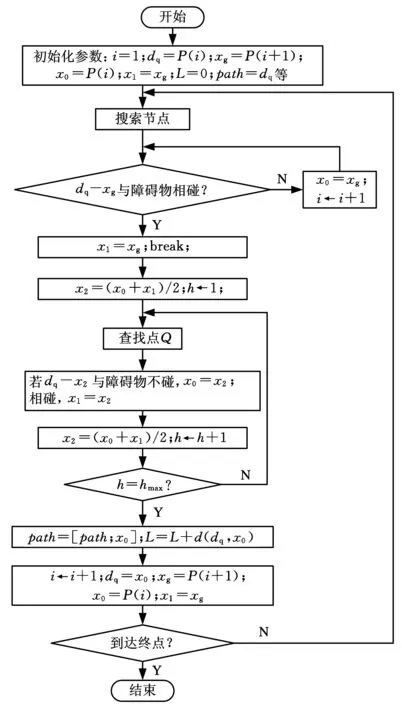
图5　二分法插值优化计算流程

4　装配路径规划实例

为验证算法求解装配路径规划问题的性能，本文用两个实例进行了验证，目标零件与障碍物采用轴向包围盒包围进行避障。

图6为减速器装配中零件螺钉的初始路径求解，图7为安装架装配中零件栏杆的初始路径求解，图中①为装配初始路径，②为优化后的路径。

图6　减速器装配路径规划与优化

图7　安装架装配路径规划与优化

由图6、图7可知，目标零件通过寻找障碍物外的可行栅格进行路径规划；由表1可知，利用蚁群算法能够快速求解出零件在复杂环境下的装配初始路径，整个计算过程用时0.30～0.55 s，蚁群算法具有群体智能等优势，将其应用于路径规划中有很高的求解效率。

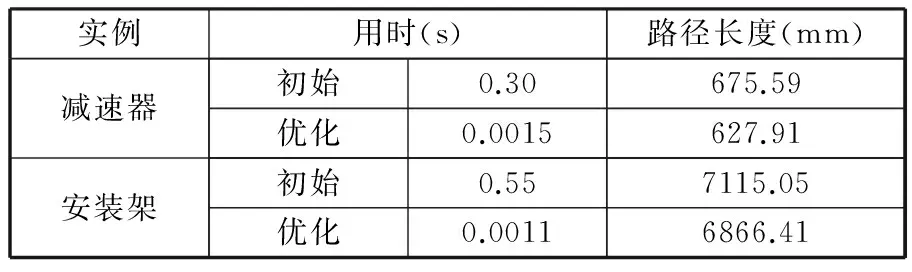
表1　装配路径规划及优化实例结果

对比表1中初始与优化用时及路径长度可得，用二分法插值优化后的路径长度明显比初始路径要短，而且二分法插值优化用时极短，在1.1～1.5 ms之间，显示出了很高的求解效率，优化后的路径是一条较为平滑的路径，更加符合装配实际。

5　结论

(1)本文基于蚁群算法对三维复杂环境下的装配路径规划问题进行了详细的分析，规划出一条避开障碍物的装配初始路径，并对求解得到的初始路径提出采用二分法插值优化方法以缩短路径长度，仿真结果取得了良好的效果。

(2)装配路径规划过程中，在处理目标零件与障碍物的碰撞信息时，通过是否发生碰撞来选择目标零件的可行邻域，并没有充分利用碰撞方向、碰撞点等信息，如何利用上述信息来更有效地规划装配路径将在以后的工作中进一步探索。

[1]Wang L, Keshavarzmanesh S, Feng H Y, et al. Assembly Process Planning and Its Future in Collaborative Manufacturing: a Review[J]. The International Journal of Advanced Manufacturing Technology, 2009, 41(1/2): 132-144.

[2]Geng Junhao, Jia Xiaoliang, Tian Xitian, et al. Assembly Path Planning Method Based on Lightweight Model[J]. Advances in Intelligent and Soft Computing, 2010, 66: 27-40.

[3]余剑峰，程晖，姚定，等.复杂产品装配顺序评价的路径反馈方法[J].西北工业大学学报，2009，27(1)：24-29.Yu Jianfeng, Cheng Hui, Yao Ding, et al. A Path Feedback Method for Evaluating the Assembly Sequence of Complex Products[J]. Journal of Northwestern Polytechnical University, 2009, 27(1): 24-29.[4]管凌峰.薄膜蒸发器三维参数化设计及其CAE研究[D].南京：南京工业大学，2006.

[5]田立中，付宜利，马玉林，等.装配路径规划中基于动态坐标的A*搜索算法[J].计算机集成制造系统，2002，8(4)：316-319.

Tian Lizhong, Fu Yili, Ma Yulin, et al. A*Search Arithmetic Based on Dynamic Coordinate in Assembly Path Plan[J]. Computer Integrated Manufacturing Systems, 2002, 8(4): 316-319.

[6]田富君，田锡天，耿俊浩，等.基于视点跟随的装配路径规划与干涉检查研究[J].中国机械工程，2011，22(15)：1810-1814.

Tian Fujun, Tian Xitian, Geng Junhao, et al. Assembly Path Planning Method Based on Viewpoint Tracking and Collision Detection[J]. China Mechanical Engineering, 2011, 22(15): 1810-1814.

[7]陈成军，周以齐，曲斌.基于力反馈的虚拟示教式机械手臂装配路径规划方法[J].系统仿真学报，2009，21(10)：2945-2950.

Chen Chengjun, Zhou Yiqi, Qu Bin. Assembly Path Planning for Robot Arm Based on Force Feedback Virtual Teaching Method[J]. Journal of System Simulation, 2009, 21(10): 2945-2950.

[8]Christiand, Yoon J, Kumar P. A Novel Optimal Assembly Algorithm for Haptic Interface Applications of a Virtual Maintenance System[J]. Journal of Mechanical Science and Technology, 2009, 23(1): 183-194.

[9]Ali M, Babu N, Varghese K. Collision Free Path Planning of Cooperative Crane Manipulators Using Genetic Algorithm[J]. Journal of Computing in Civil Engineering, 2005, 19(2): 182-193.

[10]Aguinaga I, Borro D, Matey L. Parallel RRT-based Path Planning for Selective Disassembly Planning[J]. The International Journal of Advanced Manufacturing Technology, 2008, 36(11/12): 1221-1233.

[11]Comes J, Jaillet L, Simeon T. Disassembly Path Planning for Complex Articulated Objects[J]. IEEE Transactions on Robotics, 2008, 24(2): 475-481.

[12]Dorigo M, Maniezzo V, Colorni A. Ant System: Optimization by a Colony of Cooperating Agents[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 1996, 26(1):29-41.

[13]Liu Haicheng, Li Yuan, Yu Jianfeng, et al. Path Planning Algorithm for Assembly of Complex Product Based on V-Map and Ant Colony Optimization Algorithm[C]//2010 3rd International Conference on Advanced Computer Theory and Engineering (ICACTE). Chengdu, 2010: V5-398-V5-402.

[14]Wang J F, Liu J H, Zhong Y R. A Novel Ant Colony Algorithm for Assembly Sequence Planning [J]. The International Journal of Advanced Manufacturing Technology, 2005, 25(11/12): 1137-1143.

[15]Liu Shirong, Mao Linbo, Yu Jinshou. Path Planning Based on Ant Colony Algorithm and Distributed Local Navigation for Multi-robot Systems[C]//Proceedings of the 2006 IEEE International Conference on Mechatronics and Automation. Luoyang, Henan, 2006: 1733-1738.

[16]刘密，刘检华，何永熹，等.复杂结构条件下的装配路径求解与优化技术[J].机械工程学报，2013，49(9)：97-105.

Liu Mi, Liu Jianhua, He Yongxi, et al. Research on Assembly Path Planning and Optimization of Complex Structures[J]. Journal of Mechanical Engineering, 2013, 49(9): 97-105.

(编辑王艳丽)

Assembly Path Panning and Optimization under Complex Environments

Jiang KangHu Long

Hefei University of Technology,Hefei,230601

In order to solve the problem of assembly path planning in three-dimensional complex environments, a model of planning space was established by using grid method and the ant colony algorithm was applied to obtain the initial path to avoid obstacles. The dichotomy interpolation optimization was proposed to reduce the original assembly path length. The obstacle avoidance was achieved by using the axis-aligned bounding boxes between target part and obstacles in the planning process. Some example tests were carried out on the assembly path planning and optimization to verify the effectiveness and feasibility of the proposed algorithm by achieving a shortest smooth collision-free path.

assembly path planning; planning space; ant colony algorithm; dichotomy interpolation optimization

2014-01-13

国防基础科研计划资助项目(A1120110003)；国防技术基础计划资助项目(Z312011B003，Z312012B001，B3120110500)

TP391DOI：10.3969/j.issn.1004-132X.2015.05.011

姜康，男，1974年生。合肥工业大学交通运输工程学院副教授。主要研究方向为数字化设计与制造、系统建模与仿真、信息与控制等。发表论文10余篇。胡龙，男，1989年生。合肥工业大学交通运输工程学院硕士研究生。