应用三向测量数据的深空探测器实时滤波定位算法
2015-10-28淡鹏李恒年李志军
淡鹏李恒年李志军
(1宇航动力学国家重点实验室,西安 710043)(2西安卫星测控中心,西安 710043)
应用三向测量数据的深空探测器实时滤波定位算法
淡鹏1,2李恒年1李志军2
(1宇航动力学国家重点实验室,西安 710043)(2西安卫星测控中心,西安 710043)
三向测量数据是深空探测器的一类重要观测数据,文章采用不敏卡尔曼滤波(UKF)算法实现了应用三向测量数据的深空探测器实时滤波定位计算,给出了三向测量体制下的观测模型及观测预测值计算方法,建立了动力学及非动力学两种方式下的滤波预测模型。利用嫦娥三号探测器的实测数据对算法进行了有效性验证,结果表明,文章所给出的观测及预测模型建立方法,适用于三向测量数据,动力学建模算法的稳定性与抗野值能力优于非动力学建模算法,但复杂度又高于非动力学建模方法。上述研究结果对深空探测器的定位或定轨计算具有一定的参考价值。
深空探测器;三向测量数据;实时滤波;定位算法
1 引言
在深空探测器定位数据源中,除了常用的甚长基线干涉测量(VLBI)[1]数据外,利用扩频及S频段统一测控(USB)设备获得的外测测量值也是一类重要的观测数据。由于深空探测任务中电磁波传播时延较长[2],以及地球自转等因素影响,测站有时无法接收到对应的发射信号,使得传统的双向测距体制应用受限,这时就须要通过不同测站的收发进行外测距离及距离变化率的测量。另外,深空目标的扩频及USB外测测角数据精度较差,在定位计算中较少使用,此时就要通过3个测站的测距来几何确定探测器的位置,此种情况一般采用主站发射上行信号,经应答机相干转发后,两个副站及主站同时接收下行信号的方式进行距离测量。在深空任务中,将这种通过一个测站发送上行,另一个测站(或多个测站)接收下行信号进行距离测量的体制称作三向测量,而将一个测站自发自收测量的情况称作双向测量[3]。
三向测量数据的测量元素包括三向测距(距离和)及三向测速(距离和变化率),是深空探测的一类重要的观测数据,在国内外的深空探测任务中有着广泛的应用,如美国NASA在“阿波罗”飞船落月过程中对三向数据的使用[4],以及我国嫦娥三号探测器的三向测量应用等。文献[5]对三向多普勒数据建模,并将其应用到轨道确定计算中。目前,深空三向测量数据在实时定位计算中的应用,多集中于几何计算方法(计算原理类似于三站单程测距几何定位),其应用受几何关系制约,且受数据野值影响大,从而会影响位置曲线的光滑度。为解决上述问题,本文将卡尔曼滤波方法引入三向测量数据定位计算中,并以嫦娥三号探测器飞行背景为例,给出了不同方式下的滤波定位算法及计算结果。
2 实时定位算法
卡尔曼滤波是非线性系统估计[6]的一种有效解决途径,在实时定位计算中有着广泛的应用。其包含了多类不同的滤波算法,如应用较广的扩展卡尔曼滤波(EKF)、不敏卡尔曼滤波(UKF)、容积卡尔曼滤波(CKF)和粒子滤波(PF)等。其中,UKF算法以采样变换为基础,采用卡尔曼滤波框架,对数据点进行确定性采样,而不必直接对函数进行线性化处理,因而具有实现过程简单、避免繁琐的雅可比矩阵求导计算、收敛速度较快和对噪声适应能力强等特点,是实时滤波轨道计算中使用较多的一种方法,因此本文计算中采用这种算法。
UKF算法[7]计算过程包含采样点计算、状态及观测预测、均值与协方差更新和状态更新等步骤,提供了一个通用计算框架,使用时要根据应用背景、观测值类型等对状态及观测模型进行具体设计。考虑到深空探测器飞行过程复杂(如嫦娥三号探测器包括了中途修正、近月制动、动力下降等多个阶段),有时较难进行动力学建模,本文在应用三向测量数据进行UKF滤波计算的过程中,状态外推模型的建立分别采用了动力学建模及非动力学建模的算法。
2.1 三向测量观测模型及观测预测值计算

图1 距离和的测量示意Fig.1 Sketch map for measuring range sum
由于距离和及距离和变化率数据的时标(记为TE)均打在收端站。考虑到电磁波传播时延,其对应的探测器时间(记为TN)、发端站时间(记为TS)必不相同,滤波计算中须要由探测器飞行的当前状态X及滤波状态外推模型进行外推及迭代计算求得。迭代出3个时标后,由信号发端站、信号收端站大地坐标即可计算出两站分别在TS和TE时刻的地心惯性坐标系位置rS和rE,以及速度矢量又由滤波器状态外推模型可计算出TN时刻探测器的位置rN和速度这样就可以得到TE时刻距离和的预测值ρ的表达式。

距离和变化率的预测值为
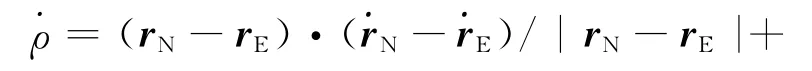

2.2 动力学建模算法
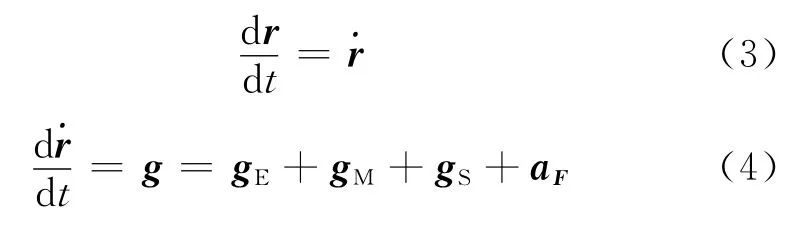
式中:g为总的加速度;gE,gM,gS分别为地球引力、月球引力、太阳引力及光压摄动力产生的加速度。
根据牛顿力学公式,aF=F/m,求导可得设F在一定时间内保持恒定或为小偏差变化量,则有可得到将其记为b,表示单位质量的质量变化率。由于现阶段推力作用是靠质量的减小产生的(消耗燃料产生推力),而即为比冲Isp,进而可推导出,其中的大小,a为加速度大小。据此,可定义滤波计算的系统状态为X=则可得到轨道机动过程增广的动力学模型为
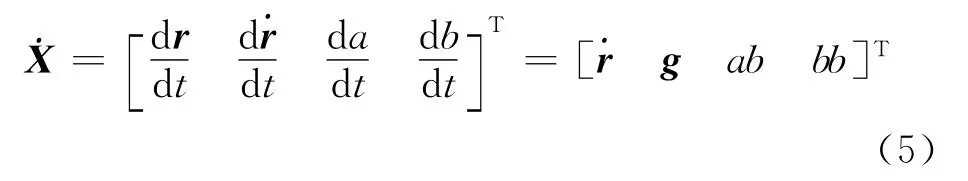
对于矢量aF,可由探测器惯性坐标系下的姿态四元数求得本体坐标系到惯性坐标系的转换矩阵[9](记为M),以及已知的推力方向在探测器本体坐标系的方向矢量(记为Fb),得到惯性坐标系下单位推力矢量aF0=MFb,然后乘上推力加速度大小a求得。
滤波状态的外推可直接通过对式(5)中的模型进行积分运算完成。
2.3 非动力学建模算法
机动目标滤波跟踪计算中,常采用纯数值拟合及统计方法进行非动力学建模计算,这方面应用较多的目标运动估计模型主要有多项式模型[10]和当前统计模型[11]等。以当前统计模型为例,可定义系统状态为其中为加速度矢量,则k时刻到k+1时刻的系统状态外推方程为

式中:Φ(k)为状态转移矩阵;U(k)为输入的状态矩阵;为当前加速度均值;w(k)为离散白噪声序列,其相关计算方法参见文献[11]。
由当前模型算法,状态转移矩阵的一种自适应表达式为

式中:T为数据采样的时间间隔。
2.4 自适应处理方法
滤波计算往往需要一定的时间进行状态收敛,在探测器机动过程中,为了更快地响应机动状态变化的情况,要在UKF计算过程中进行自适应处理。为此,本文在动力学建模及非动力学建模滤波计算过程中采用了以下方法。
(1)根据滤波“新息”[12-13]理论,实现自适应处理要重视“新息”作用,为此,在UKF计算的状态协方差矩阵(记为PXX)更新中引入渐消因子S(S>1),使得PXX适度放大,达到更重视新数据的作用。修正后UKF中状态协方差矩阵PXX计算公式为

式中:Q为状态噪声协方差矩阵;W(i)为第i个采样点的权值;为第i个采样点的状态估计,为状态预测均值。
(2)工作状态已知时,可进行适当的干预,如在轨道控制的点火点及熄火点处,对状态协方差矩阵进行重置,使其快速适应运动加速度突变的情况。
(3)如果滤波器连续多帧出现数据方差检验失败,可认为发生机动,此时采用协方差矩阵重置的方式予以适应。
2.5 算法对比
在应用深空三向测量数据进行实时定位计算中,分别采用动力学建模及非动力学建模的算法进行UKF的状态模型建立,从式(3)~(7)可见,动力学建模算法是对探测器受力运动的加速度进行建模,而非动力学建模算法直接采用多项式拟合或数据统计的方法进行建模与预估,因而在难以进行受力分析的情况下,动力学建模算法应用常常受到限制,但是因为它的外推模型相对精确,抗野值能力会好于非动力学建模算法。
3 算法验证及分析
为了验证算法的可行性,分别使用嫦娥三号探测器中途修正、近月点制动变轨、动力下降过程的实测数据进行滤波计算。
3.1 中途修正计算
对2013年12月3日嫦娥三号探测器中途修正变轨进行滤波计算,此次变轨只有2个测站的双向测量数据,计算时只使用距离和、距离和变化率两类观测量,并采用以下两种算法。动力学建模算法:进行轨道控制过程的动力学建模,在点火点与熄火点进行状态协方差矩阵重置,以加强对状态变化的自适应。非动力学建模算法:采用非动力学建模的当前统计模型进行计算。两种算法计算的轨道半长轴变化曲线如图2所示,图中时间轴给定为相对于点火开始点的秒数。由于非动力学建模算法的滤波发散,计算结果错误,因此图2中未给出对应曲线。
从计算结果来看,少于3个测站时,对于无测角的距离和、距离和变化率观测数据,此处的动力学建模算法是可行的,能够得到正确的结果;而非动力学建模算法出现滤波发散问题,计算失败,其原因在于仅用2个测站的距离和在几何关系上难以进行定位计算,而动力学建模算法外推模型相对精确,因而对测量元素较少的观测数据具有较强的适应能力。另外,从图2中可见,由于使用了自适应处理,在变轨开始点与结束点附近建模算法较好地实现了状态变化的快速响应。
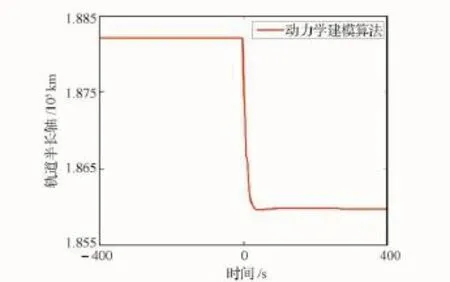
图2 中途修正变轨半长轴曲线Fig.2 Semi-major axis curve of midway orbit correction
3.2 近月制动过程计算
对2013年12月6日嫦娥三号探测器近月制动变轨(将月球J2000惯性坐标系轨道从双曲线变为椭圆)时喀什、佳木斯、三亚测站的三向测量实测距离和数据进行滤波,采用动力学建模与非动力学建模算法,计算的轨道偏心率变化曲线如图3所示(时间轴给定为相对于北京时间17:46的秒数)。
从图3中看出,两种算法的结果均反映出了偏心率调整过程(因模型及参数原因,算法结果误差大小不一致),因而对于3个测站的三向距离和数据,这两种算法均是可行的,且动力学建模算法曲线的光滑度要好于非动力学建模算法。

图3 近月制动变轨偏心率变化曲线Fig.3 Eccentricity curve of perilune orbit controlling
3.3 动力下降过程计算
嫦娥三号着陆器在2013年12月14日成功完成了动力下降及月球软着陆,使用北京时间21:05—21:13的喀什、佳木斯、三亚测站的三向测量数据(包括距离和及距离和变化率两种观测量)进行UKF计算,计算时采用非动力学建模算法的当前统计模型、多项式模型两种状态模型进行滤波实现(因为较难进行动力学建模,所以此处不使用动力学建模算法)。滤波计算的着陆器动力下降高度曲线如图4所示(高程计算时相对月面平均半径,时间轴采用相对北京时间21:00的秒数)。
从图4中看出,对动力下降过程三向测量数据滤波,当前统计模型与多项式模型的计算结果相当,两种结果均是可用的,但受制于实际数据测量及误差修正的精度,两种滤波曲线震荡均较大。对此问题的解决途径,除了提高数据处理精度外,还可通过引入其他类型的高精度测量数据进行融合滤波实现(如引入激光测高数据等)。另外,21:48后只剩下2个测站对着陆器进行跟踪,滤波直接发散(图中未给出)。

图4 动力下降高度曲线Fig.4 Height curve of descent to lunar surface
4 结论
本文对应用深空三向测量数据的滤波算法进行了阐述,从嫦娥三号实测数据滤波计算结果可得到以下结论:
(1)对三向测量数据,直接以距离和、距离和变化率作为观测量的做法是可行的,给出的应用深空三向测量数据的动力学建模及非动力学建模算法是有效的。
(2)采用非动力学建模算法时,计算结果受测量条件影响大,当只有距离和及距离和的变化率,而没有测角数据时,至少要有3个测站才能正确定位。
(3)对于三向测量数据滤波,动力学建模算法抗野值能力和稳定性要好于非动力学建模算法。
(4)由于双向测量可认为是三向测量的一种特例,因此本文算法可直接应用于双向测量计算中。
三向测量数据是深空探测的一类重要观测数据,但此类数据误差源较多,数据误差修正计算将对滤波定位精度产生显著影响,需要更精确的修正处理,也可通过引入其他观测量进行状态约束或融合计算来提高精度。因此,后续的研究重点是数据误差的精确修正及三向测量与其他各类数据(如VLBI等)的融合计算。
(
)
[1]李金岭,张津维,刘鹂,等.应用于深空探测的VLBI技术[J].航天器工程,2012,21(2):62-67 Li Jinling,Zhang Jinwei,Liu Li,et al.VLBI technique applied in deep space exploration[J].Spacecraft Engineering,2012,21(2):62-67(in Chinese)
[2]刘嘉兴.深空测控通信的特点和主要技术问题[J].飞行器测控学报,2005,24(6):1-8 Liu Jiaxing.Features and main technical issues in deep space TT&C and telecommunication systems[J].Journal of Spacecraft TT&C Technology,2005,24(6):1-8(in Chinese)
[3]黄磊,王宏,樊敏.三向测量技术在深空探测中的应用研究[J].飞行器测控学报,2012,31(3):6-10 Huang Lei,Wang Hong,Fan Min.Application of three-way measurement in deep space exploration[J].Journal of Spacecraft TT&C Technology,2012,31(3): 6-10(in Chinese)
[4]Smith E S,Morinelli P J.Analysis of three-way Doppler tracking data from the Lunar Reconnaissance Orbiter mission[C]//Proceedings of SpaceOps 2010 Conference.Washington D.C.:AIAA,2010:309-318
[5]曹建峰,黄勇,胡小工,等.深空探测中多普勒的建模与应用[J].宇航学报,2011,32(7):1583-1589 Cao Jianfeng,Huang Yong,Hu Xiaogong,et al.Modeling and application of Doppler data in deep space exploration[J].Journal of Astronautics,2011,32(7):1583-1589(in Chinese)
[6]Julier S J,Uhlmann J K.Unscented filtering and nonlinear estimation[J].IEEE Aerospace and Electronic Systems,2004,92(3):401-422
[7]潘泉,杨峰,叶亮,等.一类非线性滤波器——UKF综述[J].控制与决策,2005,20(5):481-489 Pan Quan,Yang Feng,Ye Liang,et al.Survey of a kind of nonlinear filters—UKF[J].Control and Decision,2005,20(5):481-489(in Chinese)
[8]李恒年,李济生,黄永宣.有连续推力控制的卫星轨道确定算法[J].系统工程与电子技术,2010,32(9): 1957-1961 Li Hengnian,Li Jisheng,Huang Yongxuan.On-line orbit determinative method for satellites with continuous thrust acceleration[J].Systems Engineering and Electronics,2010,32(9):1957-1961(in Chinese)
[9]李恒年.地球静止卫星轨道与共位控制技术 [M].北京:国防工业出版社,2010 Li Hengnian.Geostationary satellite orbital analysis and collocation strategies[M].Beijing:National Defense Industry Press,2010(in Chinese)
[10]淡鹏,李恒年,张智斌.一种火箭外测弹道实时重建的自适应滤波算法[J].弹箭与制导学报,2013,33(6): 188-190 Dan Peng,Li Hengnian,Zhang Zhibin.An adaptive Kalman filtering algorithm applied to real-time computing of rocket external ballistics[J].Journal of Projectiles,Rockets,Missiles and Guidance,2013,33(6):188-190(in Chinese)
[11]隋红波,房晓颖,吴瑛.改进的当前统计模型及自适应跟踪算法[J].雷达科学与技术,2008,6(3):202-205 Sui Hongbo,Fang Xiaoying,Wu Ying.A modified adaptive tracking algorithm based on current statistic model[J].Radar Science and Technology,2008,6(3):202-205(in Chinese)
[12]周卫东,乔相伟,吉宇人,等.基于新息和残差的自适应UKF算法[J].宇航学报,2010,31(7):1798-1804 Zhou Weidong,Qiao Xiangwei,Ji Yuren,et al.An innovation and residual-based adaptive UKF algorithm[J].Journal of Astronautics,2010,31(7):1798-1804(in Chinese)
[13]淡鹏,李恒年,张定波,等.基于多元非完备信息的实时滤波定轨方法[J].飞行力学,2014,32(3):283-288 Dan Peng,Li Hengnian,Zhang Dingbo,et al.Realtime filtering orbit method based on multiple incomplete observation[J].Flight Dynamics,2014,32(3): 283-288(in Chinese)
(编辑:夏光)
Real-time Filtering Positioning Algorithm Using Three-way Measurement Data for Deep Space Probe
DAN Peng1,2LI Hengnian1LI Zhijun2
(1 State Key Laboratory of Astronautic Dynamics,Xi'an 710043,China)(2 Xi'an Satellite Control Center,Xi'an 710043,China)
The three-way measurement data is one kind of important observation data for deep space probe.By using this type of data,an algorithm based on UKF(unscented Kalman filter)is presented to calculate real-time position of deep space probe.The observation model and forecast method using three-way measurement are given including the implementation method with dynamic modeling and non-dynamic modeling.Then the measured data of Chang'e-3 are used to test and verify the proposed algorithm.The results indicate that the observation and forecast modeling method is correct and feasible,and that the stability and anti-outliers capability of dynamic modeling are higher than those of non-dynamic modeling,but the dynamic modeling's complexity is high.The algorithm can be as a reference in deep space probe's positioning and orbit determination.
deep space probe;three-way measurement data;real-time filtering;positioning algorithm
V557.1
A DOI:10.3969/j.issn.1673-8748.2015.02.004
2014-03-25;
2014-04-23
国家重大科技专项工程
淡鹏,男,硕士,高级工程师,研究方向为航天器动力学与飞行计算。Email:danpeng@126.com。
