应用聚类方法的多卫星无源时差定位算法

双炜吴巍

（1山东航天电子技术研究所，山东烟台 264670）（2海军航空工程学院，山东烟台 264001）

应用聚类方法的多卫星无源时差定位算法

双炜1吴巍2

（1山东航天电子技术研究所，山东烟台 264670）（2海军航空工程学院，山东烟台 264001）

为了提高卫星定位系统的容错能力和鲁棒性，应用聚类方法提出了一种适用于多卫星的无源定位算法。依据三站时差定位原理，将每3颗卫星编成一组，用每组中的卫星分别对地面目标进行三站时差定位；再利用聚类方法融合估计目标的位置。仿真结果表明，此算法定位精度及稳定性优于传统的三站时差定位法和最小二乘法，可减少信息的不确定性，有助于提高系统的定位效果。

多卫星；无源定位；聚类分析；时差定位

1 引言

利用卫星进行高精度测时，并用时间差来进行电磁辐射源的定位，是电磁监测领域的研究热点［1-4］，利用无源时差（TDOA）定位技术使多颗卫星协同工作，实现对地面电磁辐射目标定位的方法已被广泛研究。目前，无源时差定位方法主要有三站时差定位法和最小二乘法等。例如:文献［5］中用最小二乘法估计解算目标位置，在迭代过程中通过地理信息系统查询并不断修正目标高程。文献［6］中分析了卫星群编队飞行时地面辐射源在一定范围内的定位精度分布规律。文献［7］中提出通过对卫星过顶前后的两组弱观测数据进行综合、配对处理的非线性最小二乘（NLS）的三星座时差定位综合算法。文献［8］中提出采用基于子协方差阵加权的最小二乘法来完成卫星时差定位。文献［9］针对传统时差定位时往往会出现定位模糊的问题，提出应用独立测量数据融合的加权最小二乘法（SWLS）。由以上可知，大多数的卫星时差定位算法都是基于三站时差定位法，以及为提高定位精度而提出的一些扩展方法，这些方法在一定程度上能为提高卫星无源定位精度提供参考，但在现代复杂电磁环境中，可能会出现部分卫星测站被干扰或出现故障的情况，从而导致这些方法可能无法实现准确定位。

聚类是雷达网探测目标无源交叉定位中的一种有效方法［10］，借鉴该方法，本文提出一种多卫星无源时差定位算法，可通过信息融合来提高卫星定位系统的鲁棒性和抗干扰能力。

2 传统时差定位问题

假定用n颗卫星对某地面目标进行无源时差定位，地面目标的真实位置坐标为 （x，y，z），卫星测量主站的位置为（x0，y0，z0），第i个卫星测量辅站的位置为（xi，yi，zi），地面目标到主站的距离为r0，到第i个辅站的距离为ri，其中i=1，2，…，n—1，则

式中:

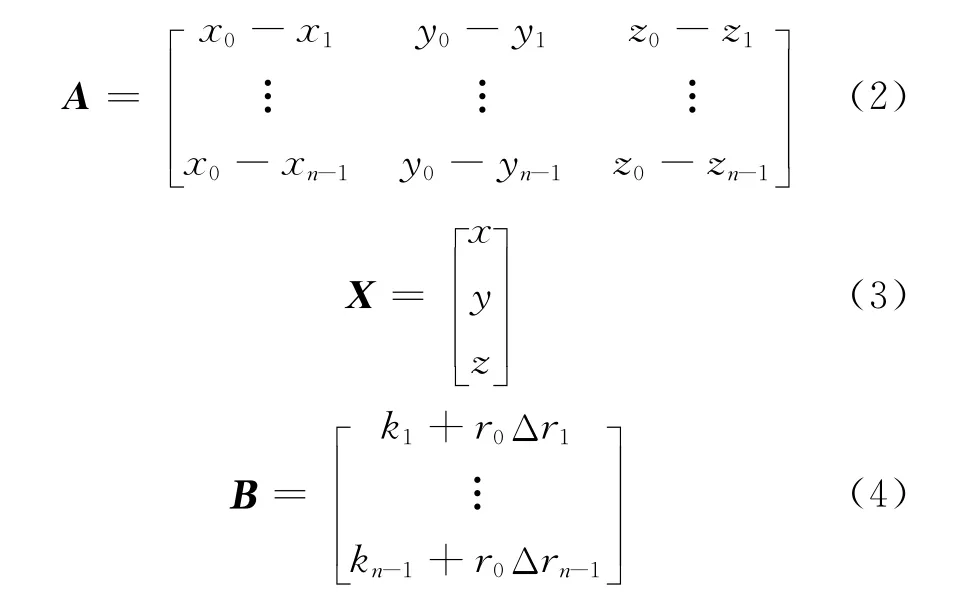
式中:

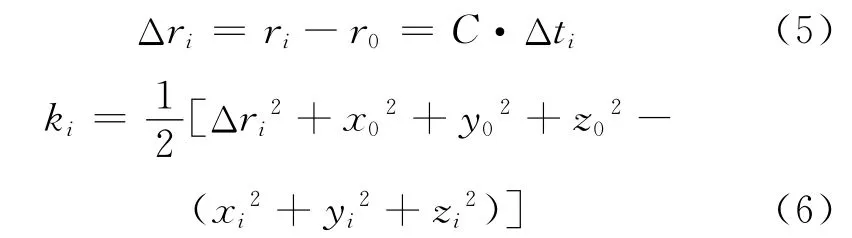
式中:Δti为目标信号到达主站和第i个辅站的时间差；C为光速。

当n＞3时，式（1）可以通过最小二乘法直接求解。

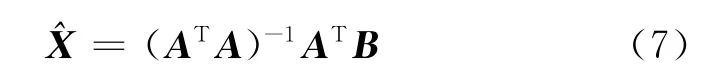
通过式（7）可直接得到目标的无源定位坐标，但由于最小二乘法只是三站时差定位法的一种扩展，它同样可能产生模糊解或无解现象，如果直接求解，会导致定位精度不稳定。另外，最小二乘法没有充分利用多颗卫星产生的冗余信息，因而没有体现出多卫星定位的优势。

3 应用聚类的多卫星时差定位算法

聚类是利用计算机技术实现“物以类聚，人以群分”目的的一种技术。具体来讲，其输入是一组没有分类的数据，且事先不知道如何分类、分成几类，通过分析数据，合理划分数据集合，确定每个数据所属的类别，把相似性大的对象聚集为一个簇。聚类的标准是使簇内数据相似度尽可能高，不同簇数据之间的相似度尽可能低。

为了解决传统三站时差定位法存在的模糊解，或者无解造成定位精度的不稳定问题，利用信息融合思想，依据基于距离的聚类方法，本文提出一种卫星组网时差定位算法，其流程如图1所示，主要步骤如下。

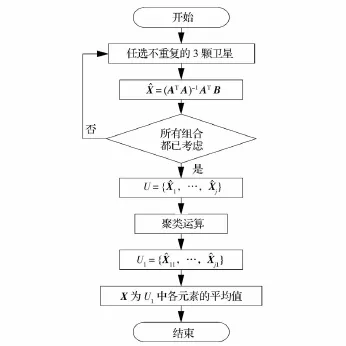
图1 算法流程Fig.1 Algorithm flow

（2）用每组卫星分别对目标进行三站时差定位，得到一个解的集合U。

（3）采用最小距离的聚类方法对解的集合U进行聚类，排除U中干扰元素，较精确地求解出目标的位置。具体步骤为:①计算U中每两个样本Ui和Uj的欧氏距离。因为Ui和Uj的距离dij与Uj和Ui的距离dji相等，所以只计算一个即可。开始时，将U的每个样本自成一类，则类Gp与类Gq之间的距离Dpq就等于两个样本间的距离dpq。②找出类间距最小的Gp的Gq，合并为一个新类，记为Gr。③计算新类与其他类的距离。新类Gr和某一类Gm的距离为Drm，则Drm=min｛Dpm·Dqm｝。④重复第②、③步，直到U中所有解都成为一类或达到设定的分类数，从而完成分类。

（4）得到正确解的集合U1，再对U1各元素取算术平均，作为目标的估计位置X。

4 仿真验证

4.1 仿真条件及结果

假设卫星数目为5颗，位置分别为s1=（0，0，400）km，s2=（30，15，450）km，s3=（30，—15，500）km，s4=（0，30，480）km，s5=（—30，0，420）km。对同一地面目标（X，Y，0），卫星测量距离均方误差为5 m，时间误差为50 ns，分别选取s1，s2，s5卫星用三站时差定位法，5颗卫星用最小二乘法和本文算法进行200次蒙特卡罗仿真，仿真结果如图2所示。用统计平均的方法求出目标在不同位置时3种方法的定位均方根误差，如表1所示。

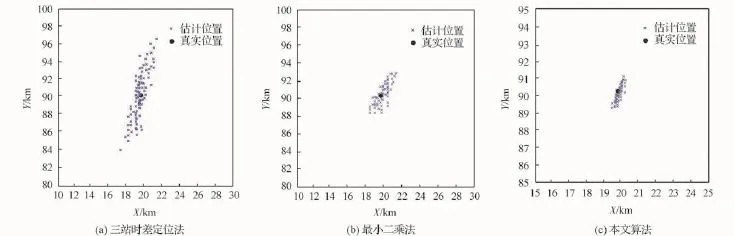
图2 定位分布Fig.2 Location distribution

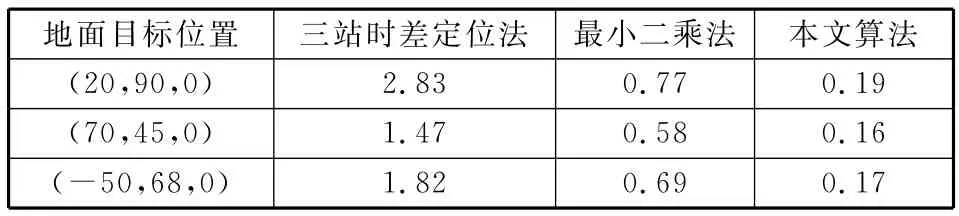
表1 不同位置目标的定位均方根误差Table 1 Root mean square errors of different position targets km

4.2 仿真结果分析

（1）对不同位置的目标，三站时差定位法的定位误差较大，对相距300～500 km的目标，误差在1 km以上（见表1），这是因为卫星相对目标的分布方式对定位结果有较大影响。而本文算法对不同位置的目标，都能得到较准确的定位结果。

（2）当时差测量结果无失真时，三站时差定位法和最小二乘法也能得到较好的定位结果，但只要有一个时差测量失真，三站时差定位法就会产生较大的偏离，而在现实环境中，由于各种噪声的存在，时差测量出现失真的情况是难以避免的。本文算法能够克服个别数据失真的影响，得到较准确的定位结果。

（3）本文算法是先分组定位，得到求解集合，可以避免出现无解现象；再通过聚类方法把求解集合中明显不合理的元素剔除掉；最后对类取算术平均，从而能克服三站时差定位时的模糊解现象。

（4）最小二乘法定位效果整体优于三站时差定位法，但定位精度及稳定性均不如本文算法。

（5）对于3种方法的计算量，本文算法中每增加1颗卫星，三站的组合数目就更多，计算量会相应增加。n颗卫星的不同组合数为颗卫星的不同组合数为组合数增加倍数为（n+1）/（n—2），随着n的增加，倍数逐渐减小，计算量增加倍数迅速减小，且逐渐趋近于1。可见，本文算法计算量虽然有所增加，但增加的倍数有限，现有的计算能力足以应付。

5 结束语

本文提出了一种适用于多卫星的无源时差定位算法，依据三站时差定位原理，将每3颗卫星编成一组，用每种组合分别对目标进行三站时差定位，再利用聚类方法来估计目标的位置，解决三站时差定位会产生模糊解和无解现象导致的稳定性不高问题，通过多卫星的冗余信息提高定位的精度和稳定性。仿真结果表明，本文算法可以对目标进行较好的定位，能提高卫星定位系统的鲁棒性和可靠性。

（

）

［1］沈如松，张育林.海洋监视卫星无源被动定位精度分析［J］.中国空间科学技术，2006，25（3）:35-39 Shen Rusong，Zhang Yulin.Analysis of passive location precision using ocean surveillance satellite［J］.Chinese Space Science and Technology，2006，25（3）:35-39（in Chinese）

［2］陆安南.对电子侦察卫星无源定位技术发展问题的思考［J］.通信对抗，2008（1）:15-20 Lu Annan.Consideration of development of passive localization by signals intelligence satellite［J］.Communication Countermeasures，2008（1）:15-20（in Chinese）

［3］江翔.无源时差定位技术及应用研究［D］.成都:电子科技大学，2008 Jiang Xiang.Research of passive TDOA location technology and application［D］.Chengdu:University of Electronic Science and Technology，2008（in Chinese）

［4］王玲.无源定位技术研究［D］.长春:长春理工大学，2009 Wang Ling.Research of passive location technology［D］.Changchun:Changchun University of Science and Technology，2009（in Chinese）

［5］李廷军，任建存，黄盛霖，等.利用最小二乘估计算法实现无源定位原理研究［C］//2009年中国智能自动化会议论文集（第三分册）.北京:中国自动化学会，2009: 129-133 Li Tingjun，Ren Jiancun，Huang Shenglin，et al.Study on estimation of passive location algorithm using least squares［C］//Proceedings of the 2009 China Intelligent Automation Conference（the Third Volume）.Beijing: Chinese Automation Association，2009:129-133（in Chinese）

［6］李晖，张钦宇，张乃通，等.地球同步轨道编队飞行卫星群无源时差定位精度分析［J］.现代电子技术，2006（z1）: 10-13 Li Hui，Zhang Qinyu，Zhang Naitong，et al.Precision of position using formation flying satellites on geosynchronous orbit［J］.Modern Electronic Techno-logy，2006（z1）:10-13（in Chinese）

［7］李悦，柳征，伍渝江.基于非线性最小二乘的三星座时差定位综合算法［J］.电讯技术，2010，50（3）:27-32 Li Yue，Liu Zheng，Wu Yujiang.Location algorithm of three-satellite constellation TDOA based on NLS［J］.Telecommunication Engineering，2010，50（3）:27-32（in Chinese）

［8］叶浩欢，柳征，姜文利.基于子协方差阵加权的三星时差定位数据综合［J］.国防科技大学学报，2012，34（5）: 63-67 Ye Haohuan，Liu Zheng，Jiang Wenli.Data integration based on sub-covariance weighting for a three-satellite TDOA-based location system［J］.Journal of National University of Defense Technology，2012，34（5）:63-67（in Chinese）

［9］吕明，郭士民.基于数据融合的时差定位处理算法的应用［J］.仪器仪表学报，2007，28（4）:100-103 Lv Ming，Guo Shimin.Application of processing algorithm of TDOA location based on data fusion［J］.Chinese Journal of Scientific Instrument，2007，28（4）:100-103（in Chinese）

［10］Kartik Trasi.Localization algorithms for passive targets in radar networks［D］.Arlington，Virginia: University of Texas，2006

（编辑：夏光）

Algorithm of Multi-satellite TDOA Passive Location Using Clustering Method

SHUANG Wei1WU Wei2
（1 Shandong Aerospace Electro-technology Institute，Yantai，Shandong 264670，China）
（2 Naval Aeronautical and Astronautical University，Yantai，Shandong 264001，China）

In order to improve the satellite positioning system fault tolerance and robustness，a passive location algorithm is presented for multi-satellite.According to the three-station TDOA location principle，three satellites are put into a group，and three-station TDOA location method is used for ground target with the satellites from each group，and then clustering method is used for fusion estimation of target position.The simulation results show that the proposed algorithm can provide better positioning the target and reduce the uncertainty of information，so the precision and stability of this algorithm are higher than those of traditional three-station TDOA location method and least squares method.

multi-satellite；passive location；clustering analysis；TDOA location

TN953

A DOI：10.3969/j.issn.1673-8748.2015.02.022

2014-05-15；

2014-09-05

山东航天基金资助项目（2013JJ006）

双炜，女，硕士，工程师，研究方向为航天测控通信和无源定位。Email：wei_shuang@126.com。