月面着陆器与巡视器同波束差分时延相对定位算法
2015-10-28樊敏黄勇李海涛王宏郝万宏陈少伍
樊敏黄勇李海涛王宏郝万宏陈少伍
(1中国科学院上海天文台,上海 200030)(2北京跟踪与通信技术研究所,北京 100094)
月面着陆器与巡视器同波束差分时延相对定位算法
樊敏1,2黄勇1李海涛2王宏2郝万宏2陈少伍2
(1中国科学院上海天文台,上海 200030)(2北京跟踪与通信技术研究所,北京 100094)
针对月球着陆巡视探测活动中的月面着陆器与巡视器的相对定位问题,建立了月面双目标相对运动方程和状态方程,给出了同波束差分时延测量量关于双目标相对位置的测量方程,进而实现了基于统计估计方法解算双目标相对位置的算法。结合嫦娥三号探测器跟踪测量条件,利用该算法开展仿真分析。结果表明:在测量弧段达到5 min以上、同波束干涉测量(SBI)时延仅有1 ns随机误差的情况下,相对定位精度可达20 m;测量数据存在3 ns系统误差时,相对定位精度为200 m,此时如果增加甚长基线干涉测量(VLBI)时延数据,可将相对定位精度提高到150 m。利用嫦娥三号实测数据处理结果验证了此算法的正确性和仿真分析的有效性,可为合理制定月面双目标相对定位策略提供参考。
月面探测;统计估计方法;相对运动方程;同波束干涉测量模型;甚长基线干涉测量
1 引言
2013年12月14日,我国嫦娥三号探测器首次实施了月球软着陆并开展月面巡视探测。嫦娥三号探测器包含着陆器和巡视器,其中,着陆器在月面软着陆后固定不动,巡视器与着陆器分离后进行巡视、勘察和采样分析工作[1]。利用地基测量数据确定着陆器和巡视器在月面的精确位置,向探测器系统和科学应用系统提供高精度的地理位置信息,以保证准确开展巡视勘察活动,是嫦娥三号任务的一项关键技术,同时也可为地外天体巡视中经典的视觉导航技术提供参考和辅助验证。我国喀什、佳木斯深空站和甚长基线干涉测量(VLBI)分系统的4个台站对嫦娥三号探测器进行跟踪测量。其中,对于着陆器,深空站可以进行测距、测速,VLBI分系统的台站可以进行双差分单向测距(ΔDOR),由此测定着陆器的位置,通过连续跟踪测量,利用统计方法还可逐步改进着陆器月面位置信息,实现着陆器高精度定位。但是,考虑质量、功耗和科学目标等因素,巡视器上配置的X频段测控数传设备不具有利用地面站进行测距和ΔDOR测量的能力,因此无法直接测定巡视器的月面位置。不过,嫦娥三号巡视器仅在着陆器附近区域(相距不超过10 km)进行勘察,由于地月距离遥远,双目标相距较近的特点使得它们相对地面站的角距离非常近,可以在地面天线的同一波束内对双目标进行跟踪测量。利用两副地面站天线对双目标同时进行测量,可以生成高精度的同波束干涉测量(SBI)数据,在美国阿波罗-16、17飞船月球探测任务中,就成功地运用SBI技术确定了月球车相对登月舱的运动轨迹[2]。因此,利用SBI数据是实现着陆器和巡视器相对定位的一种手段,须要进一步研究和实现具体的月面双目标相对定位。
传统的单点定位算法利用单历元时刻的多个测量数据进行定位解算,定位精度主要取决于测量系统的几何构型和测量数据的系统误差。由于月面目标距离地球遥远,利用地基测量系统对其跟踪测量的几何构型较差,而且地基测量数据通常有形式复杂的系统误差,因此,根据现有测量条件和数据精度,利用单点定位算法进行月面目标定位的精度仅能达到数百米量级。为了提高定位精度,可以将长弧段的测量数据归算到同一定位时刻,再进行统计平差,但归算过程无法考虑目标运动规律,从而又引入了额外误差[3]。针对这些问题,本文首先建立了双目标的相对运动方程和SBI差分时延测量方程;然后利用统计估计方法,建立解算双目标相对位置的算法并加以实现。在此基础上,根据嫦娥三号着陆器与巡视器的实际跟踪测量条件进行仿真,并对嫦娥三号探测器获取的实测数据应用此算法进行相对定位,验证了算法的正确性和有效性。
2 算法原理
利用统计估计方法对月面双目标进行相对定位,主要借鉴航天器精密定轨的理论[4-5],包括以下3个方面内容。
2.1 相对运动方程和状态方程
考虑到着陆器在月面着陆后,巡视器行进到指定探测点开展就位探测期间,两器在月心固连坐标系中均静止不动,建立的相对运动方程为

式中:Δr为着陆器位置矢量r1和巡视器位置矢量r2之差,即相对位置矢量,可用直角坐标表示,也可用月球地理坐标表示;Δr0为相对位置矢量初始值;为着陆器与巡视器相对速度矢量。
考虑相对位置、速度信息以外的其他待估参数Pg,例如,影响运动状态的物理参数、地面站坐标的几何参数和测量数据的系统误差等,定义状态矢量X的坐标为由此可得状态方程为

式中:状态矢量初值X0的坐标为[Δr00 Pg0],其中,Δr0可取标称值或根据巡视器遥测数据计算,Pg0可取理论设计值或经验值。
2.2 SBI测量模型和测量方程
SBI测量原理如图1所示,当着陆器与巡视器在角度上非常接近时,可在一副地面天线的同一主波束内被观测,使用两副天线同时对其进行观测,即可生成差分干涉测量量[6]。由于SBI的测量量能够精确确定两个目标在天平面内的相对位置信息,因此可用于相对定位[7]。
假设着陆器(记为SC1)发射信号的时刻为t1,地面站A、B接收到着陆器信号的时刻分别为t和t2。将t时刻A站接收到着陆器t1时刻发射信号的光行时记为着陆器到A站和B站的几何时延记为则着陆器t1时刻发射的信号到达B站的时刻那么,可以将信号从着陆器到B站的光行时记为同时,假设在太阳系质心惯性参考坐标系中,t时刻着陆器与巡视器(记为SC2)的位置矢量分别为RSC1和RSC2,A站和B站的位置矢量分别为RA和RB,着陆器t1时刻发射信号到A站和B站的光行时(c表示光速)可以表示为

着陆器t1时刻发射信号到达A站和B站的几何时延可以表示为

同理可得,巡视器t3时刻发射的信号到达两站的几何时延可以表示为

因此,A站和B站对着陆器与巡视器的SBI差分时延测量模型可表示为
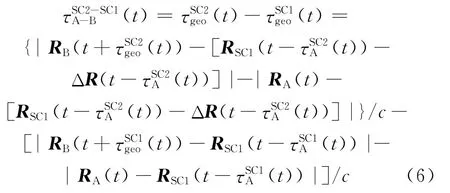
式中:ΔR为着陆器与巡视器在太阳系质心惯性参考坐标系中的相对位置矢量。

图1 着陆器与巡视器同波束干涉测量原理Fig.1 SBI measurement principle of lander and rover
可见,SBI差分时延测量量包含双目标相对位置信息,通过固定着陆器位置,利用该测量量可以解算相对位置。
由于测量模型是在太阳系质心惯性参考坐标系中建立的,相应的坐标时为太阳系质心动力学时(TDB),在进行光行时解算的时候,要计算着陆器和巡视器在太阳系质心惯性参考坐标系中的相对位置,而且要考虑各大天体引力时延等相对论影响。由于着陆器与巡视器相对状态方程是在月心固连坐标系中建立的,而且最终的待估参数为双目标在月心固连坐标系中的相对位置,因此须要考虑月心固连坐标系到太阳系质心惯性参考坐标系的转换。该转换过程涉及到的时间系统包括:地面站采用的协调世界时(UTC)、原子时(TAI)、地球时(TT)和TDB[8]。涉及到的坐标系如表1所示。
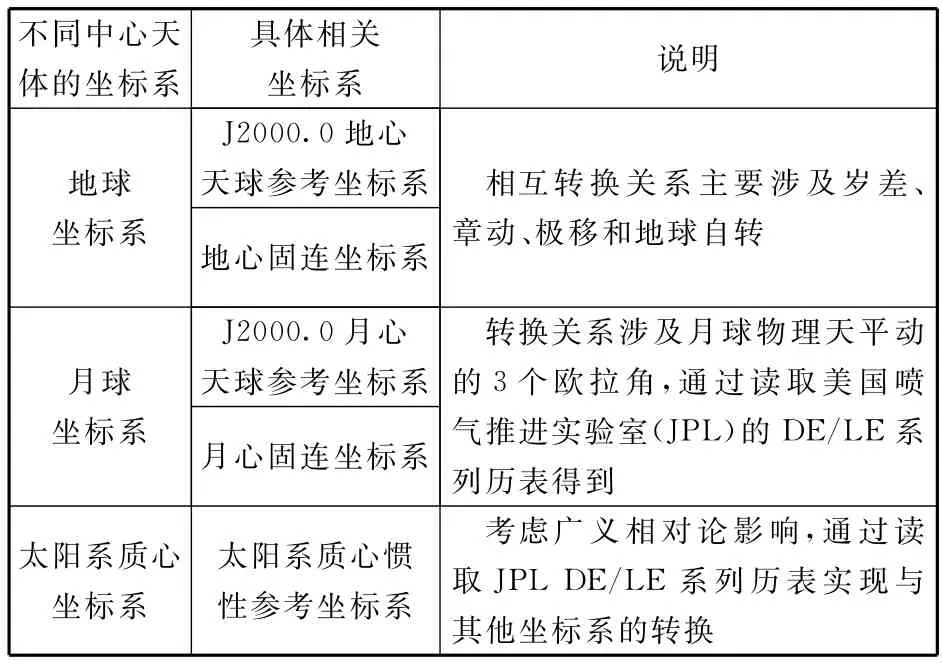
表1 相对运动方程和测量方程涉及的坐标系Table 1 Coordinate systems used in relative movement equation and measurement equation
此外,月心固连坐标系包括主轴(Principal Axes)和平轴(Mean Rotation Axes)坐标系两种[9]。其中,月球历表给出的月球天平动参数和月球重力场采用的是主轴坐标系,而国际天文联合会(IAU)定义的平轴坐标系主要用于描述月面地形和特征。目前,主轴坐标系和平轴坐标系的差异在月面小于1 km,可以根据不同的JPL DE/LE系列历表给出的转换参数进行转换。对于本文采用的DE 421历表[10],转换关系为

式中:P和M分别为主轴坐标系和平轴坐标系中点位置的坐标矢量;Ra(a代表x,y,z)表示绕坐标轴a的旋转矩阵。
基于SBI差分时延的测量模型和上述时间坐标系转换关系,可以建立对着陆器与巡视器进行连续SBI测量的测量方程。将测量值与状态矢量X之间的函数关系记为G(X,t),考虑测量噪声,则测量方程为
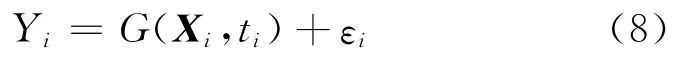
式中:Yi为ti时刻的测量量;Xi为ti时刻的状态矢量;εi为ti时刻的测量噪声。
测量模型中的函数关系是非线性的,须要对其线性化。将测量方程在参考状态X*(ti)处展开,令

式中:Φ(ti,t0)为状态转移矩阵,由于着陆器与巡视器在月心固连坐标系中相对静止,该矩阵为单位矩阵;矩阵Hi中包含双目标相对位置矢量从月心固连坐标系到太阳系质心惯性参考坐标系的转换矩阵及偏导数。
记χ0=X0—X*0,则线性化后的测量方程为

令y=[y1…yk]T,H=[H1…Hk]T,ε=[ε1…εk]T,其中k为测量量的个数,于是可将所有的测量方程总写为

2.3 统计估计方法
建立测量方程后,需要解决的问题是如何确定上述线性系统的最优估计。通常求解这类问题的直接方法是加权最小二乘批处理算法。根据加权最小二乘估计理论,如果已知待估计参数χ0的先验估计和先验估计的加权矩阵,则批处理算法解算的χ0的“最佳”估值为
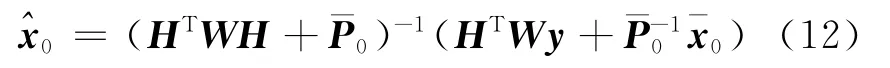
式中:W为权矩阵。
至此,完成了基于月面目标运动规律的统计估计相对定位算法,实现了对着陆器与巡视器相对位置的解算。对于嫦娥三号着陆器,考虑到其着陆后可以利用较长弧段的深空站测距、测速,以及三向测量和VLBI分系统ΔDOR干涉测量数据,解算出高精度的月心固连坐标系位置信息,因此可增加对着陆器位置的先验约束来解算着陆器与巡视器的相对位置。同时,还可以考虑利用目前高精度的月面数字高程模型(DEM)提供高程信息,如美国的ULCN2005模型[11]和我国自主研制的DEM模型[12-13]等,增加相对位置中的高程约束来解算双目标的相对位置。
3 仿真分析与验证
利用FORTRAN程序实现了上述双目标定位算法。根据嫦娥三号着陆器与巡视器的跟踪测量条件,在完成两器分离后,着陆器定向天线向地面发射数传信号,而巡视器在开展就位探测期间(每次约20 min),其测控数传设备也将发射数传信号,地面站可以利用这些单向数传信号对双目标进行SBI干涉测量,以及对单目标进行VLBI干涉测量和单向测速。考虑数传信号的设计形式和实现方式,目前对双目标的SBI干涉测量时延精度为1 ns,对单目标的VLBI干涉测量时延精度为1 ns,对单向测速精度为5 cm/s。针对上述实际情况,仿真生成了在一个跟踪弧段内上海、北京、昆明、乌鲁木齐4台站的SBI和VLBI干涉测量时延数据,以及喀什、佳木斯深空站的测速数据,具体仿真条件如表2所示。在此基础上,利用本文算法对双目标相对定位精度进行仿真分析。

表2 仿真分析条件Table 2 Simulation analysis terms
3.1 利用SBI数据相对定位
根据SBI差分时延的测量模型式(6)可知,SBI差分时延数据除包含双目标相对位置信息外,还包含着陆器本身的位置信息,因此,仅利用SBI差分时延数据进行相对定位时,要增加对着陆器位置的先验约束来解算着陆器与巡视器的相对位置。表3和表4给出了不同测量弧段和不同解算策略下的仿真计算结果。其中,以着陆器着陆点为坐标原点的北东地坐标系中,X方向为当地正北方向,Y方向为当地正东方向,Z方向与X方向和Y方向构成右手系。
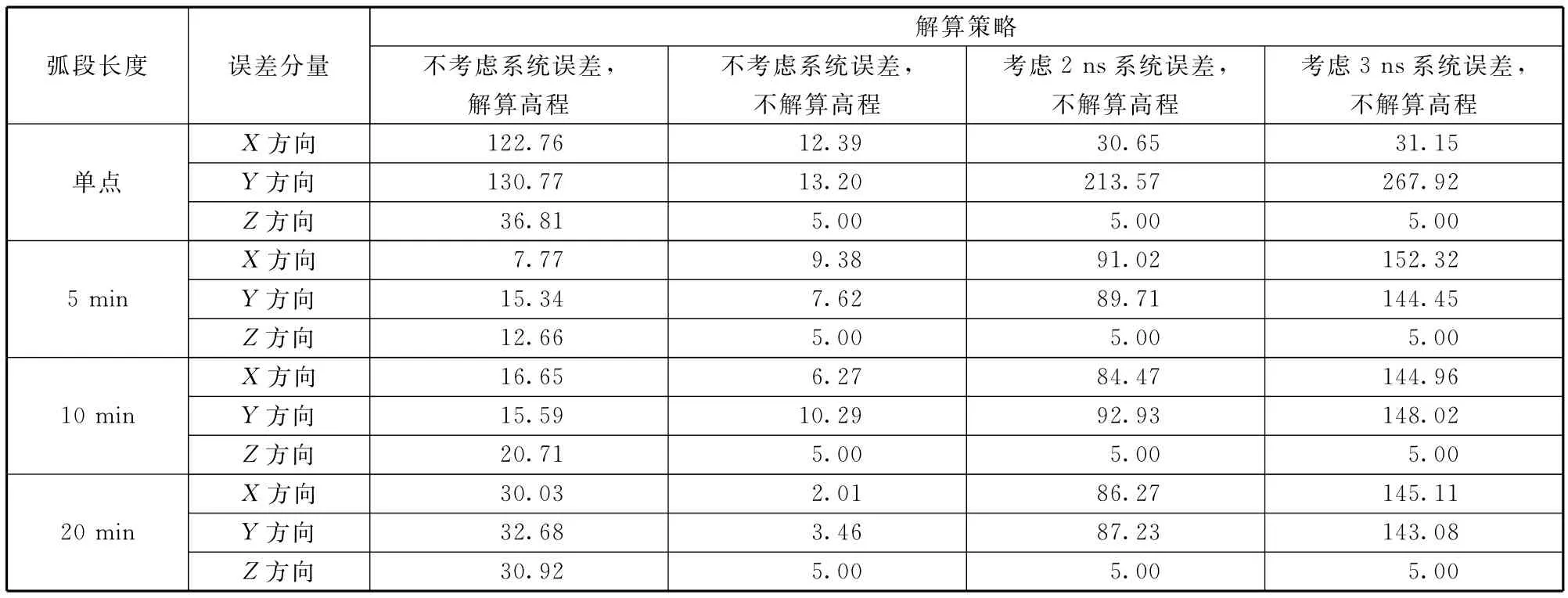
表3 利用SBI数据进行相对定位的仿真分析结果Table 3 Simulation analysis results of relative position determination using SBI data m
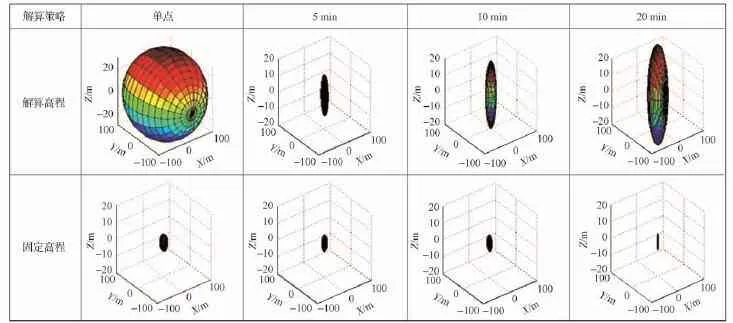
表4 解算高程和固定高程的相对定位仿真误差椭球比较Table 4 Comparison for error ellipsoid of simulation analysis results of relative position determination between estimated and fixed altitudes
可以看出:
(1)利用高精度月面DEM模型增加高程约束,对提高相对定位精度有重要作用。不考虑SBI数据系统误差的情况下,比较同时解算相对纬度、经度和高程的情况与只解算相对纬度、经度的情况,着陆器与巡视器的相对定位误差由百米降至10 m,弧段增加到20 min时,还可达到米级。此外,通过对解算时迭代次数的统计发现,解算高程通常要迭代10次以上,而增加高程约束可以有效减少迭代次数至3~4次,从而提高计算效率。
(2)测量数据系统误差对相对定位精度影响较大。不考虑测量数据系统误差时,测量弧段增加可有效提高相对定位精度,20 min弧段的相对定位精度优于10 m。但是,当测量数据存在系统误差时,增加数据弧段对相对定位精度的进一步提高作用不大。测量弧段在5 min以上的情况下,当SBI差分时延数据系统误差为2 ns时,相对定位误差小于130 m;当系统误差为3 ns时,相对定位误差小于210 m。
综合考虑上述两点,在着陆器与巡视器双目标相对定位时,VLBI分系统应保证获取5 min以上的SBI数据,并尽可能消除测量系统误差,在解算相对位置时,考虑DEM模型增加高程约束,以提高着陆器与巡视器的相对定位精度。
3.2 利用VLBI和SBI数据联合相对定位
考虑到仅利用SBI数据进行相对定位时,要增加对着陆器位置的先验约束以解算着陆器与巡视器的相对位置,而实际上,地面站在对双目标进行SBI测量的同时可以获取单目标的VLBI时延数据。因此,可以综合利用这两种数据进行相对定位。表5给出了5 min以上测量弧段、增加高程约束策略下的仿真计算结果。

表5 利用SBI和VLBI数据联合相对定位的仿真分析结果Table 5 Simulation analysis results of relative position determination using SBI and VLBI data m
比较表5与表3可以看出:①在测量数据没有系统误差时,增加VLBI时延测量数据对提高相对定位精度的作用不明显;②考虑SBI数据的系统误差,增加VLBI数据可将相对定位误差由210 m降低到150 m。考虑到SBI数据可能存在系统误差,因此着陆器与巡视器相对定位时,应综合利用VLBI数据来提高相对定位精度。
根据地面站对着陆器与巡视器的测量条件,VLBI分系统4个台站在对双目标进行SBI测量,以及单目标进行VLBI测量的同时,深空站可以获取对单目标的单向测速数据。为了分析单向测速数据对相对定位精度的影响,仿真分析了综合利用单目标测速和VLBI数据,以及双目标SBI数据进行相对定位的误差,如表6所示。
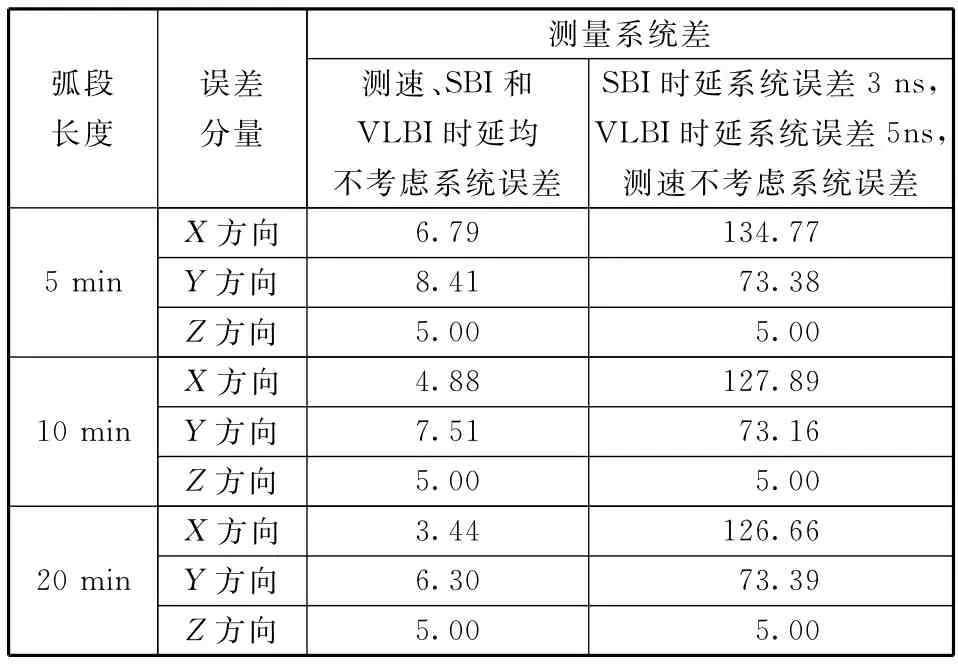
表6 利用测速和SBI及VLBI数据联合相对定位的仿真分析结果Table 6 Simulation analysis results of relative position determination using range rate,SBI and VLBI data m
通过比较表5和表6可见,对于5 min以上测量弧段,采用增加高程约束的相对定位策略,无论是否考虑测量数据的系统误差,加入测速数据对相对定位精度的影响在厘米级,远小于相对定位本身能够实现的精度。因此,在着陆器与巡视器相对定位时,可以不采用深空站的测速数据。
2013年12月14日21:12,嫦娥三号探测器成功实施月面软着陆,之后着陆器与巡视器分离,测控系统获取了实测数据。通过对2013年12月15—24日获取的测量数据进行分析,可得SBI数据随机误差约为1 ns,系统误差约为2 ns。根据本文算法,采用第2.3节增加高程约束的策略,利用实测数据进行相对定位,以精度达到厘米级的视觉导航系统二维相对定位结果为评估基准进行分析,结果如图2所示。从初步分析的10个弧段的相对定位结果来看,最大偏差约为156 m,最小偏差约为53 m,与表3中仿真分析的结果基本吻合,验证了本文算法的正确性和仿真分析结果的有效性。
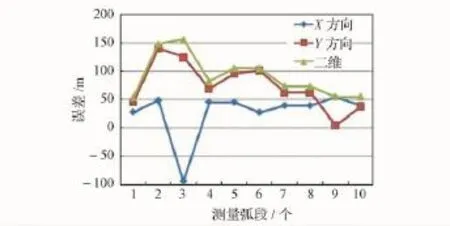
图2 嫦娥三号着陆器与巡视器实测数据相对定位精度Fig.2 Precision of relative position determination using measurement data of Chang'e-3 lander and rover
4 结束语
本文提出的月面着陆器与巡视器相对定位算法,源于经典的航天器动力学统计定轨方法,根据月球的平动和转动模型建立双目标在空间的运动模型,不必考虑复杂的空间飞行动力学建模问题,运动模型的精度仅取决于月球物理天平动参数和月面地理参数的精度,而目前国际通用的月球历表和地理参数精度已达到厘米级,因此完全满足相对定位需求。同时,该算法不同于常规的几何定位归算算法,可以利用双目标相对运动方程精确计算任意时刻的测量值,从而提高解算精度。利用此算法对嫦娥三号探测器实测数据进行处理分析,相对定位结果与仿真结果一致,表明算法正确、有效。利用本文算法对着陆器与巡视器实际测量条件开展仿真分析,可以为合理、有效地制定月面双目标相对定位策略提供参考,后续也可以进一步用于着陆地外天体的两探测器之间的相对定位。
(
)
[1]刘庆会,陈明,熊蔚名,等.基于超高精度多频点同波束VLBI技术的月球车精密相对定位[J].中国科学:物理学力学天文学,2010,40(2):253-260 Liu Qinghui,Chen Ming,Xiong Weiming,et al.High accurate relative positioning of lunar rover using super high accurate multi point frequencies same beam VLBI[J].Science of China,Scientia Sinica Physical,Mechanical& Astronomical,2010,40(2):253-260(in Chinese)
[2]Salzberg I M.Tracking the Apollo lunar rover with interferometry techniques[J].Proceedings of the IEEE,1973,61(9):1233-1236
[3]黄勇,胡小工,李培佳,等.运动学统计定位方法应用于月球着陆器的精密定位[J].科学通报,2012,57(28/29):2686-2692 Huang Yong,Hu Xiaogong,Li Peijia,et al.Precise positioning of the Chang'e-3 lunar lander using a kinematic statistical method[J].Chinese Science Bull,2012,57(28/29):2686-2692(in Chinese)
[4]李济生.航天器轨道确定[M].北京:国防工业出版社,2003:255-258 Li Jisheng.Spacecraft orbit determination[M].Beijing: National Defense Industry Press,2003:255-258(in Chinese)
The paper is written in a good language, the logic is clear and the subject and results are discussed graphically and meaningfully.
[5]刘林,胡松杰,王歆.航天动力学引论[M].南京:南京大学出版社,2005:55-58 Liu Lin,Hu Songjie,Wang Xin.An introduction of astrodynamics[M].Nanjing:Nanjing University Press,2005:56-58(in Chinese)
[6]Thornton C L,Border J S.深空导航无线电跟踪测量技术[M].李海涛,译.北京:清华大学出版社,2005:3-5 Thornton C L,Border J S.Radiometric tracking techniques for deep space navigation[M].Li Haitao,translated.Beijing:Tsinghua University Press,2005:3-5(in Chinese)
[7]董光亮,郝万宏,李海涛,等.同波束干涉测量对月面目标相对定位[J].清华大学学报(自然科学版),2010,50(7):1118-1124 Dong Guangliang,Hao Wanhong,Li Haitao,et al.Relative position determination on the lunar surface using same-beam interferometry[J].Journal of Tsinghua University(Science&Technology),2010,50(7): 1118-1124(in Chinese)
[8]Petit G,Luzum B.IERS conventions(2010)[R/OL].[2013-10-01].http://www.iers.org/TN36/
[9]Archinal B A,A'Hearn M F,Bowell E,et al.Report of the IAU Working Group on cartographic coordinates and rotational elements:2009[J].Celestial Mechanics and Dynamical Astronomy,2011,109(2):101-135
[10]Folkner W M,Williams J G,Boggs D H.The planetary and lunar ephemeris DE421[R/OL].[2013-12-01].http://tmo.jpl.nasa.gov/progress_report/42-178/178C.pdf
[11]Archinal B A,Rosiek M R,Kirk R L,et al.Completion of the unified lunar control network 2005 and topographic model[C]//Proceedings of the 37th Annual Lunar and Planetary Science Conference.Houston:Lunar and Planetary Institute,2006
[12]平劲松,黄倩,鄢建国,等.基于嫦娥一号卫星激光测高观测的月球地形模型CLTM-s01[J].中国科学:物理学力学天文学,2008,38(11):1601-1612 Ping Jinsong,Huang Qian,Yan Jianguo,et al.Lunar topographic model CLTM-s01 from Chang'e-1 laser altimeter[J].Science of China,Scientia Sinica Physical,Mechanical&Astronomical,2008,38(11):1601-1612(in Chinese)
[13]李春来,任鑫,刘建军,等.嫦娥一号激光测距数据及全月球DEM模型[J].中国科学:地球科学,2010,40(3):281-293 Li Chunlai,Ren Xin,Liu Jianjun,et al.Laser altimetry data of Chang'e-1 and the global lunar DEM model[J].Science of China,Earth Science,2010,40(3): 281-293(in Chinese)
(编辑:夏光)
Algorithm of Relative Positioning for Lander and Rover on Lunar Surface Using Differential Time-delay of SBI
FAN Min1,2HUANG Yong1LI Haitao2WANG Hong2HAO Wanhong2CHEN Shaowu2
(1 Shanghai Astronomical Observatory,Chinese Academy of Sciences,Shanghai 200030,China)
(2 Beijing Institute of Tracking and Telecommunications Technology,Beijing 100094,China)
For relative positioning of the lander and the rover in lunar soft landing and surface reconnaissance exploration,an algorithm is presented that can be used in relative positioning for two objects based on the statistical estimation method by establishing the relative kinematic equation,state equation and the measurement model of SBI(same beam interferometry).A simulation of this algorithm is carried out based on emulational measurement data of Chang'e-3 TT&C system.The result shows that the relative positioning error can be 20m when stochastic noise of SBI delay data is 1ns and tracking arc is longer than 5min.Moreover,if there is a bias of 3ns in SBI delay data,the relative positioning error increases to 200m,which can be declined to 150m by adding VLBI delay data.The validity of the algorithm and the effectiveness of the simulation are proved by the analysis of Chang'e-3 measurement data.The algorithm can support effectively determining a strategy of relative positioning of two objects on lunar surface.
exploration on lunar surface;statistical estimation method;equation of relative movement;model of same beam interferometry;very long baseline interferometry
V556
A DOI:10.3969/j.issn.1673-8748.2015.02.003
2014-04-23;
2014-08-13
国家自然科学基金(11473056,11403076)
樊敏,女,工程师,研究方向为航天测控、轨道动力学。Email:fanmin@bittt.cn。
