空间机器人路径规划综合优化方法

金宗耀 谭春林

（北京空间飞行器总体设计部，北京 100094）

空间机器人路径规划综合优化方法

金宗耀 谭春林

（北京空间飞行器总体设计部，北京 100094）

执行复杂操作的空间机器人常具有冗余自由度，从而可以在执行任务过程中通过关节参数的合理规划对指定目标进行优化。振动和操作灵活性是评价空间机器人性能和任务完成质量的两项重要指标，而关节力矩的大小是影响振动的重要因素。文章提出了一种路径规划综合优化方法，在对机器人末端运动速度进行优化处理的基础上，利用其冗余自由度，对关节力矩和评价操作灵活性的条件数指标进行综合优化。以平面3自由度机器人为对象建立数学模型，并在零重力环境下对相同任务进行数学仿真。仿真结果显示，采用文章优化方法，关节力矩与操作灵活性指标均得到了有效优化，验证了所提出方法的有效性。

空间机器人；冗余自由度；路径规划；综合优化

1 引言

空间机器人由于经常要在复杂任务约束下执行操作，因此多具有冗余自由度。具有冗余自由度的机器人在执行相同任务操作时，可以选择不同的路径规划方案，从而能同时满足多种约束条件，或者能有选择地优化运动过程中的多项指标［1］。其中，关节力矩（对振动有重要影响）和操作灵活性，是经常优先考虑的两个指标，尤其对于大型空间机器人，其本体的柔性不可忽略，在路径规划时对上述两项指标进行优化的结果将直接影响任务完成的质量。目前，机器人路径规划优化方法研究多集中在对运动学、动力学的单目标优化效果提升［2］，或者仅针对运动学问题的多目标优化［3-4］，以及对动力学问题的多目标优化上［5］，而对运动学与动力学目标综合优化问题的研究较少，且已有的研究在优化过程中容易出现优化目标相互影响、顾此失彼的情况［6］。

本文提出了路径规划时的一种运动学与动力学综合优化方法，从末端速度和零空间向量出发，对机器人完成任务过程中的关节力矩与操作灵活性评价指标进行综合优化。通过计算仿真，对比了同一仿真模型在零重力空间环境下完成相同任务时未优化和采用本文优化方法的仿真结果，证明了本文方法的有效性。

2 仿真对象及其数学模型

仿真对象设定为一个平面3自由度机器人，末端只跟踪平面2自由度位置向量，因此具有一个冗余自由度，对象示意图及坐标系如图1所示。由于冗余自由度机器人路径规划原理与方法相同，因此本文仿真模型验证的原理与方法可以推广到多自由度大型冗余空间机器人。

图1 平面三自由度机器人Fig.1 Planar 3-DOF robot

图1中:l1，l2，l3是机器人3个臂杆的长度，均为1 m；假设机器人臂杆质量为零，其质量全部集中在关节末端，末端质量分别为m1，m2，m3，均为1 kg；q1，q2，q3分别为3个关节的运动角度。由此，可得机器人的雅克比矩阵为

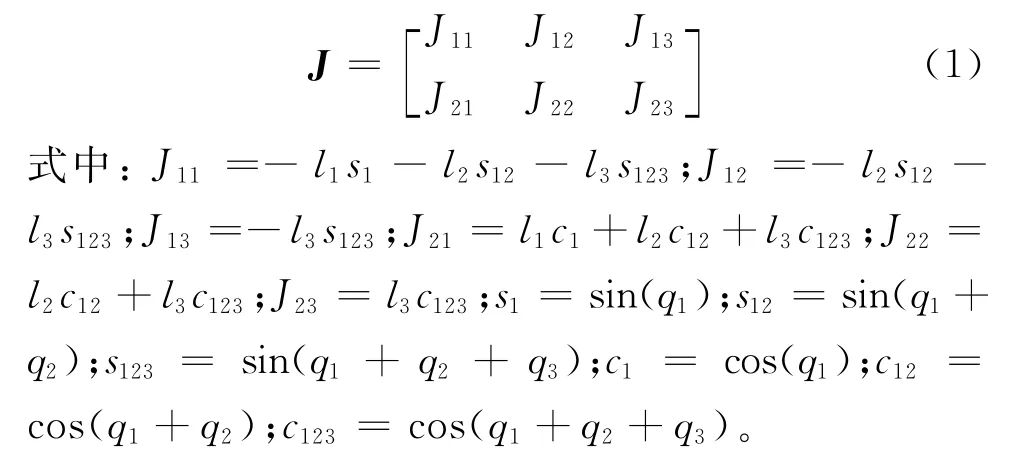
由于本文以关节力矩和操作灵活性为综合优化目标，操作灵活性优化模型可以由关节速度推导，而利用冗余自由度对关节力矩优化则必须通过关节加速度进行推导，因此要建立仿真对象模型与关节加速度的数学表达，以便建立的目标优化数学模型同时适用于关节力矩优化与操作灵活性优化。冗余自由度机器人的速度方程为

式中:χ为末端位置坐标；q为关节角度向量。

将式（2）对时间求导［7］，得到关节加速度为

式中:J+为雅克比矩阵的广义逆矩阵；I为单位矩阵；φ为方程数域中的任意向量，下文利用对φ的合理选取以及对末端速度的合理优化，达到对机器人关节力矩与操作灵活性综合优化的目的。

3 优化目标与综合优化方法数学模型

3.1 关节力矩优化

对于具有一定柔性的机器人来说，操作时所产生的不必要振动，往往对执行任务产生不利影响。关节力矩的大小及关节力矩曲线的平滑性，会对产生的振动有重要贡献，因此在执行相同任务时，减小机器人关节力矩并使力矩变化平缓，可以对抑制振动产生积极影响。

本文从两个方面优化机器人在执行任务时所需要的关节力矩。一是对机器人末端速度规划进行优化；二是利用冗余自由度对关节力矩采取限制措施，从而在保证完成相同任务的同时减小机器人操作所需的关节力矩。这样就可以在得到更小的任务操作关节力矩的同时，提高力矩曲线的平滑性。

3.1.1 末端速度优化

对于在相同时间内末端运行相同轨迹的机器人，通过对末端运动速度的合理规划，能够优化机器人关节力矩变化的平滑性和峰值的大小［8］。本文采用由抛物线过渡梯形速度规划方法处理末端运行路径，从而达到上述效果。

设运动轨迹起点时刻和终点时刻分别为0和tf，加速段和匀速段分别经历时间ta和ts，减速段和加速段对称。加速段和减速段都分为加速度增加、加速度不变、加速度减小3个过程，加速段过渡点分别为ta/3，2ta/3，ta，减速段与加速段对称。方法中规定在加速段和减速段各过渡点处速度、速度曲线斜率均相等，同时在0，ta，ta+ts，tf处斜率为零，从而保证速度曲线的平滑。由此，可以得到速度曲线方程，其中加速段的速度方程为

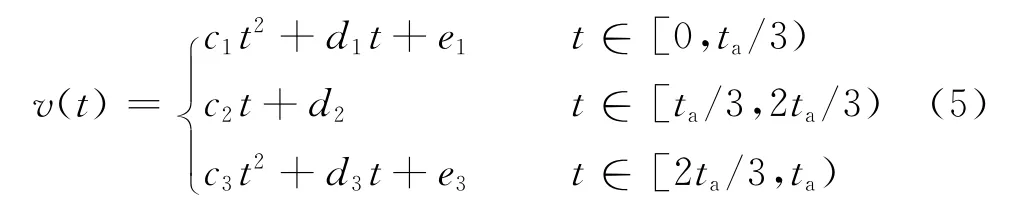
式中:c1，c2，c3，d1，d2，d3，e1，e3表示为了求取平滑曲线方程的暂定未知数。

匀速段的速度方程为

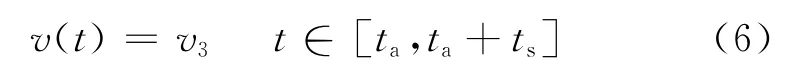
式中:υ3为匀速段速度。

减速段与加速段对称，其加速度方程可根据上述约定对速度方程求导得到。通过推导，可以得到平滑的末端速度规划曲线，从而使机器人在执行相同任务时关节力矩变化平缓，且能够部分减小峰值力矩。

3.1.2 利用冗余自由度优化关节力矩

本文采用Lagrange乘子方法利用冗余自由度对关节力矩优化，用极小化函数推导关节力矩极小化数学表达式。首先，模型中关节力矩的数学表达式为

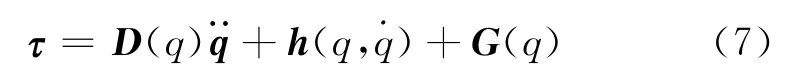
式中:D为力矩系数矩阵；h为耦合项矩阵；G为重力矩阵，此处为零矩阵。

利用极小化函数方法推导关节力矩［2］，有

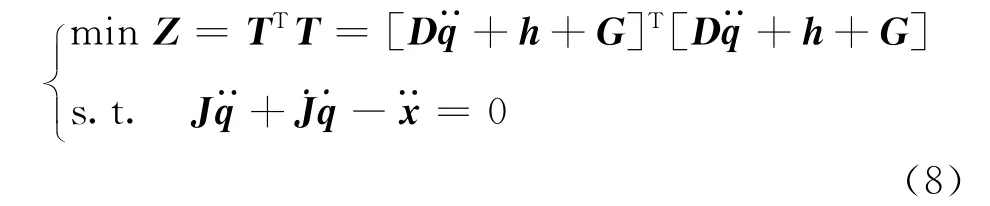
引入Lagrange乘子λ，对式（8）进行整理，得

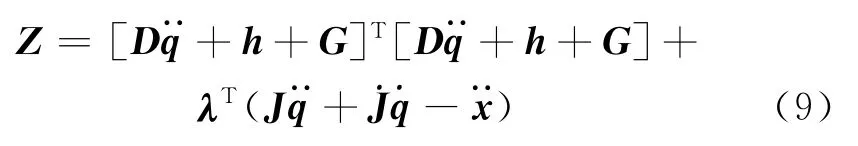
对式（9）中的Z进行极小化处理，得

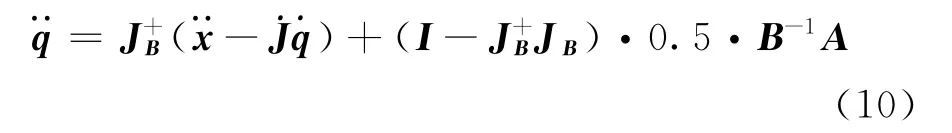
式中:考虑机器人工作在零重力环境，JB=B—1JT·（JB—1JT）—1；B=D2；A=—2Dh。

为了改善方法的稳定性，用广义逆矩阵J+代替式（10）中的整理得

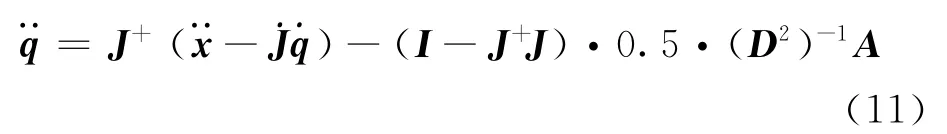
式（11）即为利用Lagrange乘子法推导的关节力矩极小化数学表达式。

3.2 操作灵活性优化

操作灵活性是衡量机器人在完成任务同时其位姿是否有利于下一步任务操作的指标，目前已有多种评价指标。本文采用文献［7］中提出的雅可比矩阵的条件数k衡量操作灵活性能量。对于冗余自由度机器人，条件数k定义为k（J）=‖J‖‖J+‖，k越接近1，矩阵性态越好，操作灵活性越好；k越大，矩阵越趋于病态，操作灵活性越差［10］。

本文采用对雅克比矩阵J的最小奇异值σm（J（q））进行优化的方法来达到改善条件数的目的。在此取最小奇异值为待优化函数，设

对雅克比矩阵进行奇异值分解并取其梯度，有

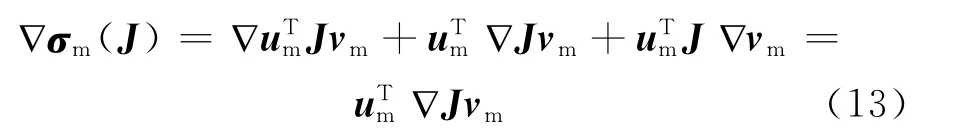
式中:um和vm分别为左、右酉矩阵。

所以有

式中:i=1，2，3。

则最小奇异值的梯度优化函数为

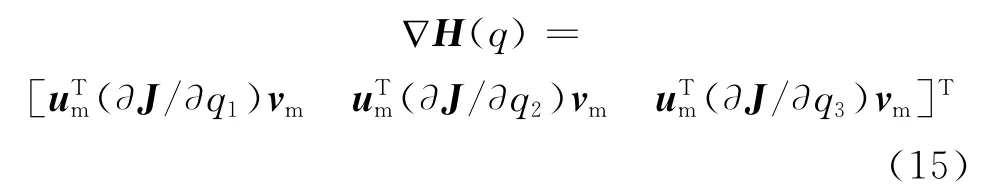
▽H（q）即为满足条件数评价方法的操作灵活性梯度函数，将其代入式（4）的数域内任意向量中，由梯度函数的数学原理可知，该函数项可以在方程中控制最小奇异值，从而降低条件数。

3.3 综合优化方法数学模型

本文希望在优化机器人路径规划的同时，对关节力矩与操作灵活性进行综合优化。第3.1和3.2节中分别推导了关节力矩优化的表达式和最小奇异值的梯度函数。式（11）与式（4）的数学表达形式相同，所以式（11）中0.5·（D2）—1A部分是方程通解中对数域中任意向量的一种选择，又由上述推导可以得到，选择的这个特殊向量可以使关节力矩达到最小。为了达到关节力矩与操作灵活性两个目标综合优化的目的，牺牲一部分力矩优化效果［11］，在其中加入对操作灵活性优化的数学表达，并通过合理选取比例系数，就可以达到关节力矩与操作灵活性综合优化的目的。其具体数学表达式为

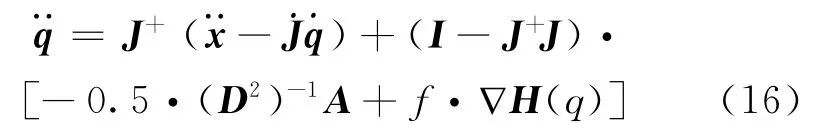
式中:f为任意系数。

4 仿真分析

在仿真分析中，将机器人的任务均设定为在10 s的时间内，末端由初始位置（2，0）运动到终点位置（1，1），对此任务进行两组仿真。在未优化组仿真中，末端速度采用基本的梯形曲线进行规划，且不对关节空间向量进行优化。在优化组仿真中，对笛卡尔空间的末端速度采用式（5）、式（6）中的平滑过渡曲线进行规划，对关节空间向量采用式（16）中的关节力矩与操作灵活性综合优化方法，其中f取为

1.2。仿真结果见图2～图5。

由图4可得:优化组仿真获得的3个关节的峰值力矩，比未优化组仿真的分别降低了约20%、30%、5%，并且力矩变化的平缓程度有所优化。由图5可得:优化组仿真获得的条件数在机器人任务执行过程中70%的时间里低于未优化组仿真获得的条件数，两者最多相差12%。

图2 末端速度Fig.2 Velocity of end-effector

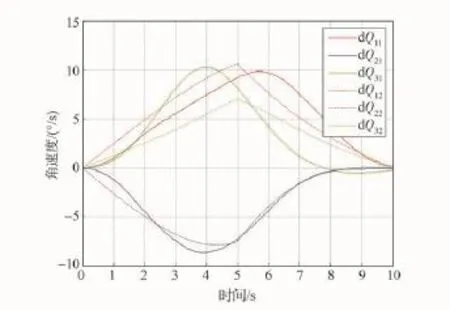
图3 关节速度Fig.3 Velocity of joints

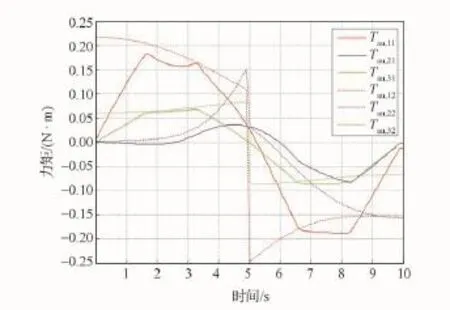
图4 关节力矩Fig.4 Torque of joints

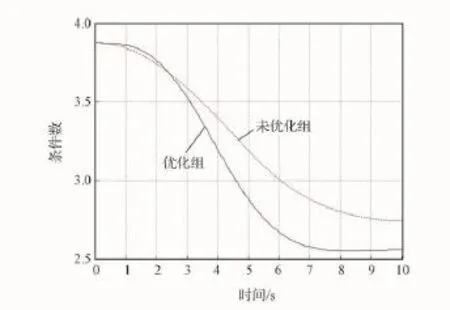
图5 条件数Fig.5 Condition numbers

5 结束语

针对大型空间机器人在执行复杂任务时经常面对复杂任务约束，并需要对多类目标进行优化的应用背景，本文选取其中实用程度较高的关节力矩和操作灵活性为优化目标，提出了一种路径规划的综合优化方法，并配合机器人末端速度平滑规划方法，以平面3自由度机器人为对象，进行了仿真分析。通过对比在零重力仿真环境下，同一模型在执行相同任务时采用本文的优化方法与不进行优化的运动路径及其相关参数仿真结果，可以证明，本文的方法能够同时对机器人的关节力矩与操作灵活性产生优化效果。本文的仿真对象及数学模型建立所应用的基本原理与数学理论具有通用性，因此本文方法在同类空间机器人运动路径规划中具有通用性。

（

）

［1］熊有伦.机器人学［M］.北京:机械工业出版社，1993 Xiong Youlun.Robotics［M］.Beijing:Mechanical Engineering Press，1993（in Chinese）

［2］Lee Heow Pueh.Motions with minimal joint torques for redundant manipulators［J］.ASME Journal of Mechanical Design，1993，115（3）:599-603

［3］余跃庆，刘林涛.多冗余度柔性机器人运动规划［J］.机械科学与技术，2003，22（4）:588-590 Yu Yueqing，Liu Lintao.Kinetic planning of hyper redundant robot［J］.Mechanical Science and Technology，2003，22（4）:588-590（in Chinese）

［4］Kazuya Yoshida.Zero reaction maneuver:flight validation with ETS-VII space robot and extension to kinematically redundant arm［C］//Proceedings of IEEE International Conference on Robotics and Automation.New York:IEEE，2001:441-446

［5］胥宏，张绪平，余跃庆.冗余度柔性机器人动力规划研究［J］.设计与研究，2002，31（5）:27-29 Xu Hong，Zhang Xuping，Yu Yueqing.Dynamic planning research of flexible and redundant robot［J］.Design and Research，2002，31（5）:27-29（in Chinese）

［6］孙奎，谢宗武，刘宏，等.梯度投影法多性能准则优化的应用研究［J］.控制与决策，2007，22（12）:1433-1440 Sun Kui，Xie Zongwu，Liu Hong，et al.Application of gradient projection method for multi-target optimization［J］.Control and Decision，2007，22（12）:1433-1440（in Chinese）

［7］陆震.冗余自由度机器人原理及应用［M］.北京:机械工业出版社，2007 Lu Zhen.Theory and application of redundant robot［M］.Beijing:Mechanical Engineering Press，2007（in Chinese）

［8］陈伟海.冗余自由度机器人优化控制研究［D］.北京:北京航空航天大学，1996 Chen Weihai.Optimization control study of redundant robot［D］.Beijing:Beihang University，1996（in Chinese）

［9］Hollerbach J M，Suh K C.Local versus global optimization of redundant manipulators［C］//Proceedings of IEEE International Conference on Robotics and Automation.New York:IEEE，1987:619-624

［10］Dubey R V，Euler J A.An efficient projection optimization scheme for a seven-degree-of-freedom redundant robot with spherical wrist［C］//Proceedings of IEEE International Conference on Robotic and Automation.New York:IEEE，1988:28-36

［11］Kazerounian K，Nedungadi A.An alternative method for minimization of the driving forces in redundant manipulators［C］//Proceedings of IEEE International Conference on Robotic and Automation.New York: IEEE，1987:1791-1706

（编辑：夏光）

Multi-objectives Optimization Method for Path-planning of Space Robot

JIN Zongyao TAN Chunlin
（Beijing Institute of Spacecraft System Engineering，Beijing 100094，China）

Space robots for complicated missions are usually redundant，so they can finish missions with different selection of joints parameters to fulfill different optimization objectives.Vibration and flexibility of movement are two important criteria for evaluating performance of space robots，and magnitude of joints torque is an important factor which can affect the vibration.For path-planning this paper proposes a method which can simultaneously optimize joints torque and condition number，based on the optimization of the velocity of robot end and by employing the redundant DOF（degree-of-freedom）of robot.A strategy for smoothing the velocity curve of end-effector is also employed in this method.A simulation study is conducted in this paper.In this study，the simulated subject is a planar 3-DOF robot in zero-gravity environment，a mathematical model is established and two results of the same mission with different path-planning are presented.By contrasting their results，effectiveness of the proposed method is proved，including the optimization of torque and condition number.

space robot；redundant degree-of-freedom；path-planning；multi-objectives optimization

TP24

A DOI：10.3969/j.issn.1673-8748.2015.02.006

2014-02-07；

2014-03-10

国家重点基础研究发展计划（973计划）（2013CB733000）和装备预先研究项目“航天器在轨服务技术”（617010105）

金宗耀，男，硕士，研究方向为航天器机械总体设计、空间机器人技术。Email：jzyyzr@126.com。