全电推进GEO卫星的变轨策略研究

田百义 雪丹 黄美丽

（北京空间飞行器总体设计部，北京 100094）

全电推进GEO卫星的变轨策略研究

田百义 雪丹 黄美丽

（北京空间飞行器总体设计部，北京 100094）

针对采用全电推进平台的GEO卫星的轨道转移问题，在给定电推进轨道控制模型的基础上，开展卫星由GTO向GEO的变轨策略研究。首先，在轨道远地点高度不变的基础上，给出了给定控制解析解的变轨策略，并给出了该种策略轨道控制律的解析解。其次，文章基于李雅普诺夫优化原理给出了优化的变轨策略，并结合仿真算例计算了该种策略控制律的数值解。在电推进优化转移策略研究的基础上，还分析了全电推进平台卫星在不同推力下的变轨时间需求。文章的变轨策略可为电推进系统在航天领域的应用提供参考。

全电推进；小推力；地球静止轨道；轨道转移

1 引言

从20世纪60年代至今，电推进技术的发展经历了原理样机研制、在轨飞行验证、工程化应用三个主要阶段，随着技术发展的深化和不断的改进优化，电推进技术已日趋成熟，并且在轨得到了广泛应用。当前，电推进技术在地球静止轨道（GEO）卫星中主要应用于南北位置保持，这是由于电推进推力较小的特点决定的。随着电推进技术的成熟，电推进技术的应用已逐渐从控制静止轨道南北位置保持向完成整个轨道转移任务的方向转变，这类应用拥有着巨大的发展前景，能够显著节省卫星携带的推进剂的质量，提高有效载荷比。然而但轨道转移与在轨位置保持的要求不同，它对电推力器的能力提出了更高的要求。电推进系统推力较小，一般在几十毫牛到几百毫牛之间，远远小于化学推进的几百牛，因此使用电推进从地球同步转移轨道（GTO）变轨至GEO的时间将长达数月，且变轨策略与采用大推力化学推进系统相比也有很大区别［1-4］。

2012年3月，波音卫星系统公司在一次商业通信卫星竞标中推出了全球首款全电推进平台——BSS-702SP平台，拉开了全电推进卫星研制的序幕。所谓全电推进，即放弃化学推进，只依靠电推进系统完成所有的轨道机动。全电推进平台正在成为未来地球静止轨道卫星的一个发展方向。

本文主要研究GEO卫星采用全电推进平台的变轨策略问题［5-7］，并以GEO卫星轨道转移任务为例，分析电推进系统进行轨道转移的能力，并给出给定控制解析解和优化的轨道转移两种策略，为我国电推进系统在航天领域的应用研究提供参考。

2 轨道控制模型

由于电推进系统提供的推力加速度位于10—3～10—5m/s2的量级，与航天器自身受到的摄动加速度处于同一量级，因此，可将电推进加速度作为摄动加速度进行处理。本文采用高斯摄动方程作为轨道控制模型［6］，形式如下:

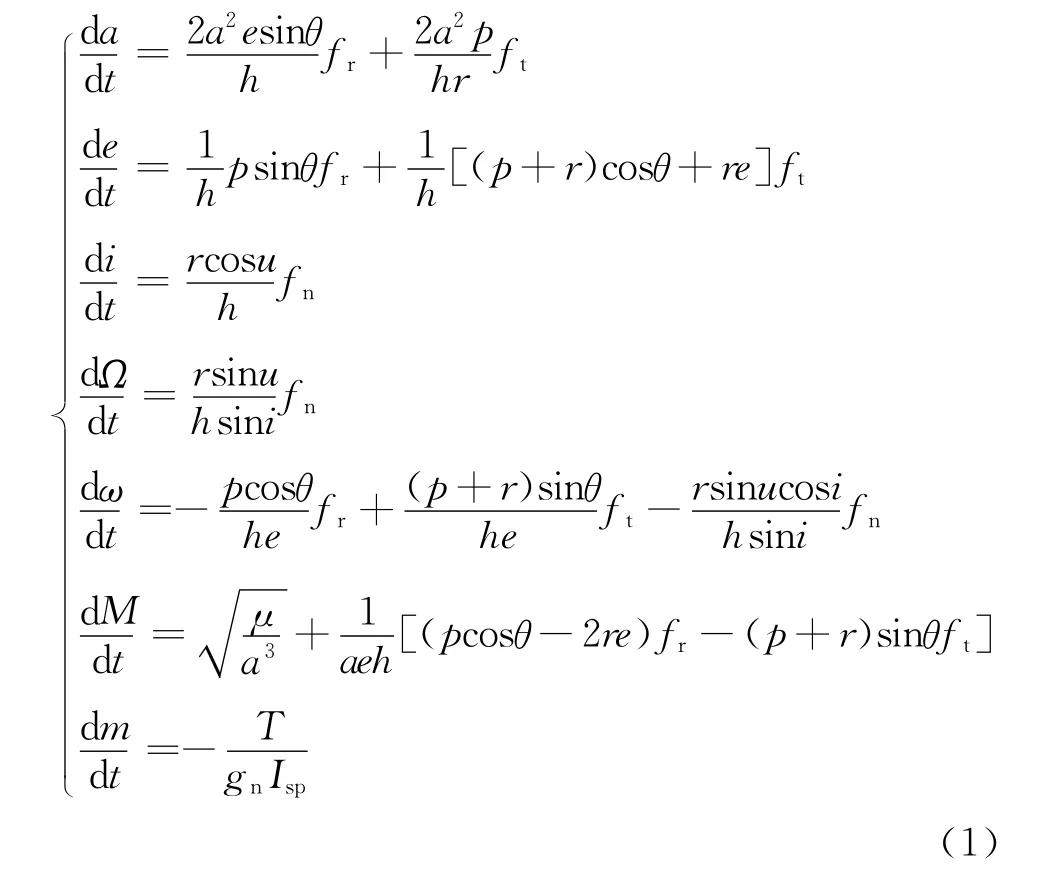
式中:a为轨道半长轴；e为轨道偏心率；i为轨道倾角；Ω为升交点赤经；ω为近地点幅角；M为平近点角；m为卫星质量；θ为真近点角；u=ω+θ，为纬度幅角；p=a（1—e2），为轨道半通径；为轨道角动量大小；为卫星地心距大小；fr，ft，fn分别为航天器径向、横向和法向控制加速度；T为发动机推力大小；Isp为发动机比冲；μ为地球引力常数。

定义控制推力角α为推力矢量在轨道面内投影与航天器地心矢径垂线方向的夹角，推力矢量指向径向为正；定义控制推力角β为推力矢量与轨道面的夹角，推力矢量指向角动量方向为正，则fr，ft，fn可表示如下。

对于GTO—GEO变轨任务，卫星的目标轨道倾角和偏心率为零，但在工程中，可对目标轨道偏心率和倾角作如下处理:

（1）当偏心率e≤1×10—5时，认为轨道偏心率到达目标值零；

（2）当倾角|i|≤1×10—5时，认为倾角到达目标值零。

由于电推进加速度大小与地球J2项摄动加速度处于同一量级，因此，本文的轨道动力学模型引入地球J2摄动模型，J2项摄动加速度在径向、横向和法向的分量如下:

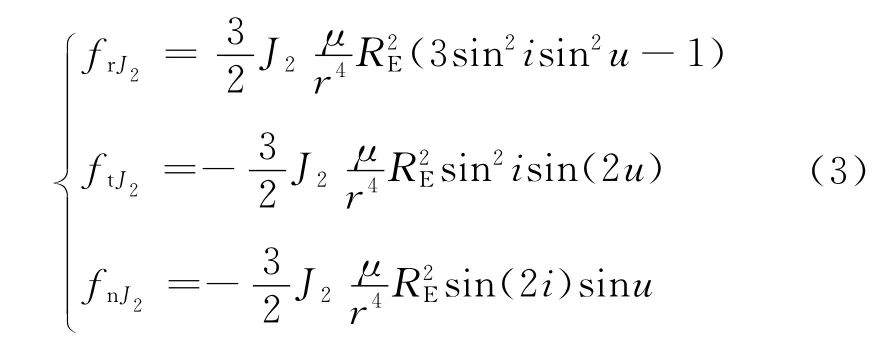
式中:常数J2取1 082.63×10—6；RE为地球赤道半径，取6 378.14 km。如果需要考虑更多的摄动力，只需在式（1）右端增加更多的摄动项，不影响本文变轨策略的制定。

3 GEO卫星轨道转移任务描述

本文针对采用全电推进方式将卫星由GTO向GEO转移的任务进行分析，给出不同轨道转移策略所需的时间和推进剂消耗。假设卫星初始轨道（GTO）参数和目标轨道（GEO）参数如表1所示。

表1 初始轨道和目标轨道参数Table 1 Initial and target orbit elements

在固定推力情况下，变轨策略的制定，主要是选择点火时间、每次点火时长及点火时的推力方向，不同的组合可以得到不同结果，对应着不同的转移时间和推进剂消耗，可按任务需求选取其中推进剂或转移时间最优的策略。GTO—GEO轨道转移任务只需要调整以下3个参数:半长轴、偏心率和倾角，下面针对这3个参数的调整提供不同的策略。

4 轨道转移策略

4.1 轨道转移解析解策略

发动机推力可分解为轨道面内和轨道法向2个分力，分别进行轨道面内调整和轨道面外调整，暂时忽略两者之间的耦合，可以分别得到控制推力角的解析解，以此作为已知控制律的变轨策略。该策略由于采用解析解，可以方便星载计算机自动控制参考使用。

4.1.1 α角解析解

轨道面内调整时，只改变GTO的近地点高度，而远地点高度不变，因此，应选择在轨道远地点附近弧段进行变轨。

变轨过程中，轨道远地点高度Ra始终不变，即Ra=a（1+e）为常值，该等式两边微分，即0。可得到

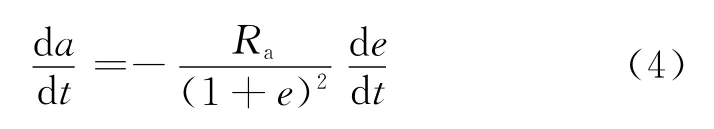
将轨道控制模型公式（1）代入，可得发动机工作在真近点角θ时的控制推力角

以GTO为例，一个轨道周期内，α角的取值变化情况如图1所示。

计算过程中，当轨道近地点高度到达目标值之后，应取卫星径向和横向推力加速度为零，即fr=0，ft=0。

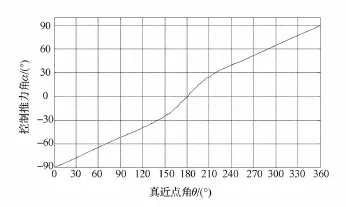
图1 一个轨道周期内α角的取值变化曲线Fig.1 Pitch steering over one period

4.1.2 β角解析解

轨道面外的转移主要表现为倾角的调整，由轨道控制模型可知，倾角调整最有效的位置位于升交点或降交点处，即卫星纬度幅角u=0或π时，取|β|=。当时，倾角的调整效率为零，此时应取|β|=0。

因此，控制推力角β可设计如下:

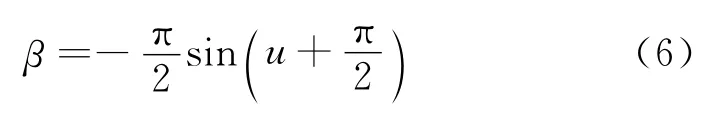
当发动机全弧段工作时，一个轨道周期内，β角的取值变化情况如图2所示。

图2 发动机全弧段工作时β角在一个轨道周期内的取值变化曲线Fig.2 Yaw steering over one period for all thrusting arc

计算过程中，当轨道倾角到达目标值之后，应取β=0，也就是fn=0。

4.1.3 变轨仿真计算结果

当卫星控制推力角α和β确定之后，卫星径向、横向和法向的推力加速度可由式（2）得出。卫星变轨过程如图3所示，变轨过程为:在时发动机开机，在时发动机关机，φ表示发动机工作弧段的长度。

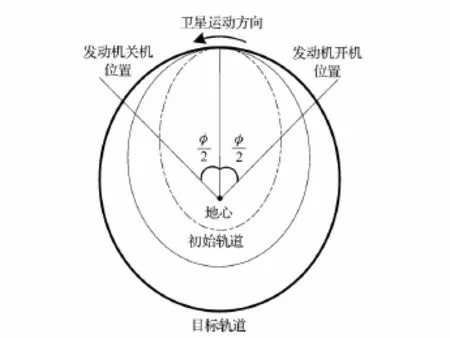
图3 GTO—GEO控制示意图Fig.3 Thrusting around apogee for GTO—GEO transfer

表2 给定解析解的变轨策略所需轨道转移时间和推进剂预算Table 2 Time and propellant budget for a given strategy GTO—GEO transfer

由表2可知，发动机工作弧段越长，所需的轨道转移时间越短，但所需的推进剂和速度增量越大。当发动机全弧段工作时，即φ=2π时，轨道转移时间最短，为417.21 d，但所需的推进剂最多，为367.67 kg。在工程中，可根据任务时间和推进剂需求情况，综合选择发动机工作弧段的长度。

以φ=2π为例，轨道半长轴、偏心率、倾角和轨道高度变化历程如图4所示。

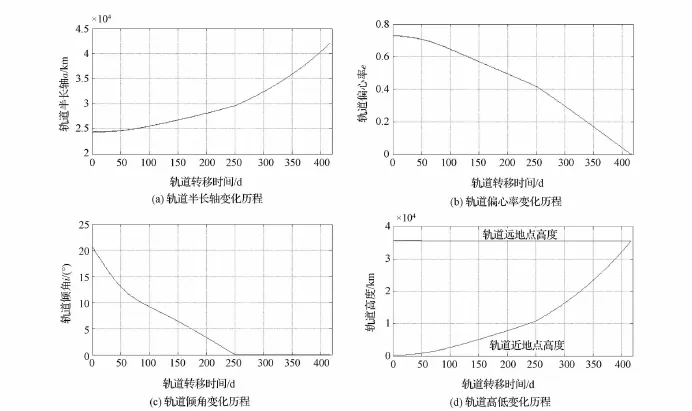
图4 变轨期间轨道参数变化历程Fig.4 Element variation over the transfers for the given strategy GTO—GEO transfer

由图4可知，采用该策略的变轨过程中，前期表现为轨道近地点高度和倾角的同时调整，待倾角到达目标值后，只进行近地点高度的调整。整个变轨过程，轨道远地点高度不变，说明了近似解析解的正确性。

4.2 轨道转移数值解析策略

4.1节给出了一种给定控制解析解的策略，所需最短变轨时间为417.21 d，对应的推进剂消耗为367.67 kg，为了进一步减少轨道转移时间，转移轨道的优化设计便显得尤为重要。本节基于李雅普诺夫优化原理进行GTO—GEO转移轨道的优化设计分析，从而得到优化的轨道控制律［8-9］。

在轨道转移过程中，主要控制对象为:半长轴a、偏心率e和倾角i，通过控制推力角α和β的设计，可实现3个变量的单独控制或耦合控制的目的，因此，控制推力角α和β可通过3个权重系数wa、we和wi来表征:

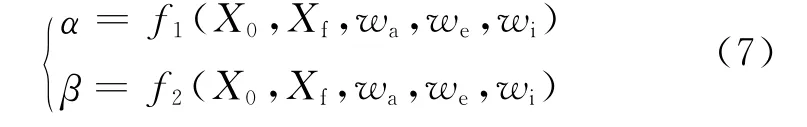
式中:X0和Xf分别为卫星初始时刻和末端时刻的状态。

不同的权重系数分配，卫星完成由初始轨道向目标轨道转移所需的时间和推进剂消耗也不同，因此，为了获得时间最优的电推进转移轨道，需对权重系数进行优化。当已知探测器初始时刻t0的状态时，对轨道控制模型（公式（1））积分，得到探测器在末端时刻tf的状态因此，当给定卫星目标轨道参数［afefif］T时，对应的电推进转移轨道优化问题便转为如下的非线性规划问题。

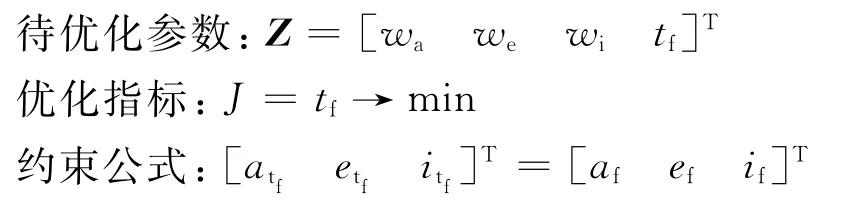
通过优化设计，GTO—GEO轨道转移任务所需的轨道转移时间和推进剂消耗情况见表3。

表3 优化的电推进轨道转移时间和推进剂预算Table 3 Time and propellant budget for optimal transfer strategy

由表3可知，整个转移任务所需的总时间为338.88 d，推进剂消耗298.44 kg，对应的速度增量为2.66 km/s。相对于给定控制律的轨道转移策略，轨道转移时间减少了18%以上，推进剂消耗量也实现了优化。可见，通过轨道转移策略的优化设计，实现了进一步减少轨道转移时间的目的。

为方便卫星总体设计参考，表4给出了200 mN、600 mN和800 mN推力对应的优化转移时间。由数据可知，当发动机推力减小至200 mN时，卫星轨道转移所需时间增至638 d，而当推力分别增大至600 m N和800 m N时，轨道转移所需时间分别减少至192 d和149 d。可见，在卫星质量固定的情况下，推力越大，轨道转移所需时间也就越短。建议卫星总体设计时综合考虑卫星轨道转移时间需求，以及卫星质量大小和推力大小约束。

图5给出了轨道半长轴、偏心率、倾角和轨道高度的变化历程，控制推力角随轨道转移时间的变化情况如图6所示。

由图5可知，采用优化转移策略，整个变轨期间都在进行轨道半长轴、倾角和偏心率的调整，三者以单调递增或递减的方式同时到达目标值。变轨期间轨道远地点高度表现为先增后减。

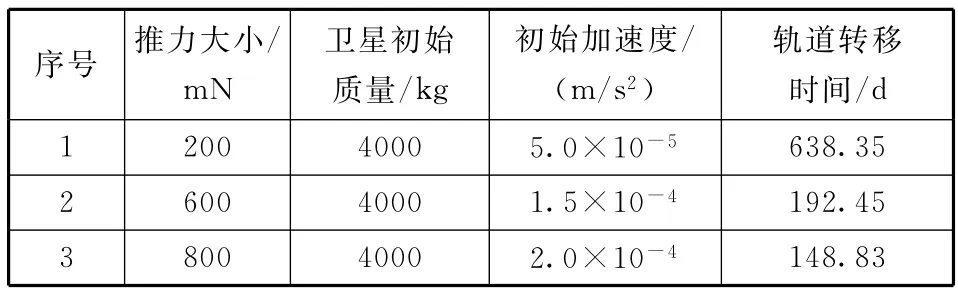
表4 200 mN、600 mN和800 mN推力所需的优化转移时间Table 4 Time budget for optimal transfer strategy with 200mN，600mN and 800mN thrust

由图6可知，轨道转移初期，控制推力角α在0°附近变化，随着轨道转移时间的增加，变化范围逐渐增大，在190 d左右，α角开始在［—180°，+180°］范围内变化，直到变轨完成；控制推力角β前期以负值为主，约为—50°。随着轨道转移时间的增加，β角变化范围逐渐增大，并呈现正负值持续时间各为变化周期的一半的现象，在190 d左右，变化范围达到最大，为［—90°，+90°］，随后，变化范围逐渐减小，当轨道倾角到达目标值后，β角为0°。

图5 变轨期间轨道参数变化历程Fig.5 Element variation during transfers for the optimal trajectory

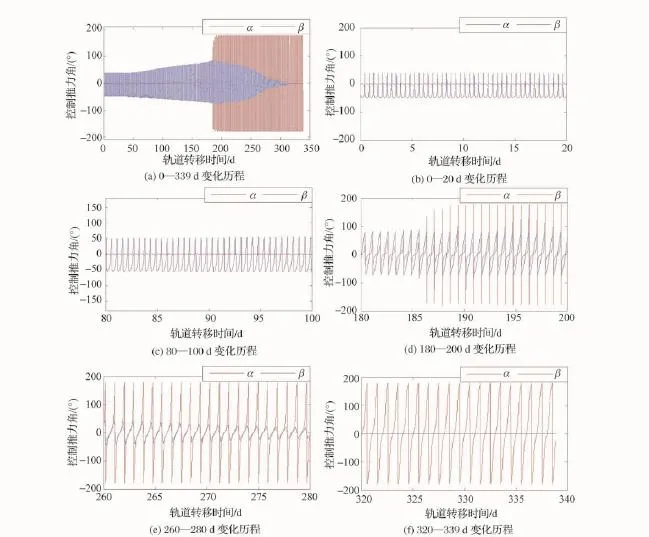
图6 优化的控制推力角随轨道转移时间的变化情况（全过程及局部放大）Fig.6 Pitch and yaw steering over the transfers for the optimal trajectory

4.3 半数值半解析策略

优化转移策略是通过数值优化的方法获得轨道转移控制律，所得结果较给定解析解的转移策略节约转移时间和推进剂消耗，具有最优的特性，但其计算量大，而且数值结果复杂，后续可根据优化结果进行控制推力角α和β的曲线拟合工作，从而获得控制律的拟合公式，以便于星载计算机自动控制解算应用。

5 结束语

针对GEO卫星采用全电推进平台的变轨策略进行了研究分析，给出了两种轨道转移策略，并对各策略的轨道控制律进行了设计，其中给定控制解析解的轨道转移策略，其控制律设计过程简单，具有解析表达式，适用于项目论证阶段电推进系统能力的分析或者推进剂约束较弱的轨道转移任务，而且方便星载计算机自动控制参考使用；而电推进优化转移策略，具有轨道转移时间和推进剂消耗最优的特性，但其控制律不具有解析表达式，需通过优化获得，设计过程复杂，可为电推进系统在工程中的应用提供依据。

本文研究表明，采用电推进方式仅需要数百千克推进剂即可完成GEO卫星轨道转移任务，相对于传统有限推力变轨方式而言，可以大量节省轨道转移段的推进剂消耗，但卫星入轨时间也大幅度延长。对于本文给定的电推力器水平，优化之后的轨道转移策略所需时间长达百天之久，这对卫星初始轨道需要重新定位，并对卫星变轨期间的长期运行管理和抗辐射等提出了新的技术挑战。

（

）

［1］张郁.电推进技术的研究应用现状及其发展趋势［J］.火箭推进，2005，31（2）:27-36 Zhang Yu.Current status and trend of electric propulsion technology development and application［J］.Journal of Rocket Propulsion，2005，31（2）:27-36（in Chinese）

［2］段传辉，陈荔莹.GEO卫星全电推进技术研究及启示［J］.航天器工程，2013，22（3）:99-104 Duan Chuanhui，Chen Liying.Research and inspiration of all-electric propulsion technology for GEO satellite［J］.Spacecraft Engineering，2013，22（3）:99-104（in Chinese）

［3］John W Dunning，John A Hamley，Robert S Jankovsky，et al.An overview of electric propulsion at NASA，AIAA 2004-3328［R］.Washington D.C.: AIAA，2004

［4］G Saccoccia，J Gonzalez.An overview of electric propulsion activities in Europe［C］//40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit.Washington D.C.:AIAA，2004:1-9

［5］R Killinger，R Kukies.Orbit raising with ion propulsion on ESA's ARTEMIS satellite［C］//38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference& Exhibit.Washington D.C.:AIAA，2002:2-14

［6］Gopinath N S，Srinivasamuthy K N.Optimal low thrust orbit transfer from GTO to geosynchronous orbit and station keeping using electric propulsion system［C］//54th International Astronautical Congress of the International Astronautical Federation.Paris:IAF，2003: 2-3

［7］Andrew V Llin.Low thrust trajectory analysis，JSC-66428［R］.Bay Area Blvd Webster:Ad Astra Rocket Company，2012

［8］任远.星际探测中的小推力转移轨道设计与优化方法研究［D］.哈尔滨:哈尔滨工业大学，2007:54-70 Ren Yuan.Design and optimization of low-thrust interplanetary transfer trajectory［D］.Harbin:Harbin Institute of Technology，2007:54-70（in Chinese）

［9］彭成荣.航天器总体设计［M］.北京:中国科学技术出版社，2011 Peng Chengrong.System design for spacecraft［M］.Beijing:China Science and Technology Press，2011（in Chinese）

（编辑：张小琳）

Orbit Transfer Strategies for GEO Satellites Using All-electric Propulsion

TIAN Baiyi XUE Dan HUANG Meili
（Beijing Institute of Spacecraft System Engineering，Beijing 100094，China）

Based on the low-thrust orbit control model，orbit transfer strategies for GEO satellites that use all-electric propulsion from GTO to GEO are analysed in this paper.Firstly，the analytical strategy is investigated based on the fixed orbit apogee，and the analytical control law is given for this strategy.Secondly，the optimal transfer strategy is studied based on the Lyapunov feedback control law，and the numerical control law is given combined with an example.Besides，the transfer time required is evaluated for different thrust according to the optimal transfer strategy，which is helpful to providing advice for the application of electric propulsion in space exploration.

all-electric propulsion；low-thrust；GEO；orbit transfer

V474.3

A DOI：10.3969/j.issn.1673-8748.2015.02.002

2014-08-25；

2015-02-09

国家重大航天工程

田百义，男，工程师，从事航天器轨道设计工作。Email：tianbaiyi@163.com。