弹簧中的图像问题探讨

毕泽

摘   要：弹簧模型是高中物理中最常考的物理模型之一，由于弹簧弹力是变力，学生往往对弹力大小和方向的变化过程缺乏清晰认识，不能建立与之相关的物理模型并进行分类，导致解题思路不清、错误率较高。弹簧和图像组合起来的题目难度比较大，学生们往往无从下手，因此针对弹簧中的图像问题本文列举了一些典型例题进行探讨。

关键词：弹簧;图像;临界;分离

中图分类号：G633.7 文献标识码：A    文章编号：1003-6148（2015）9-0036-5

题型1：F-x图

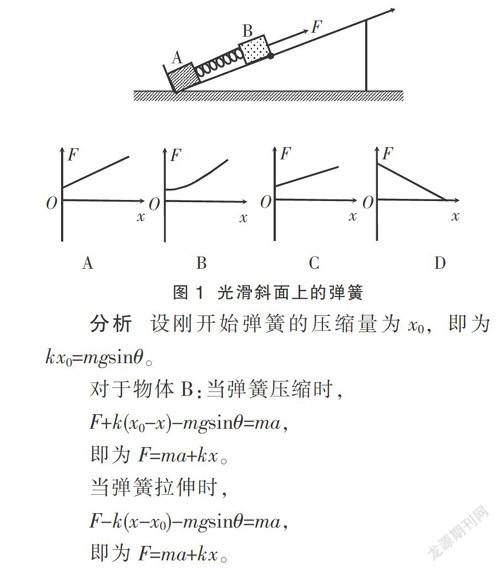
例1  如图1，光滑斜面的底端固定一垂直于斜面的挡板，质量相同的A、B两物体由轻弹簧连接，放在斜面上，最初处于静止状态。现用一平行于斜面的力F拉B物体沿斜面向上做匀加速直线运动，以B物体的初始位置为坐标原点、沿斜面向上建立Ox坐标轴，在物体A离开挡板之前（弹簧一直处于弹性限度内），外力F和挡板对A物体的支持力N随B物体的位置坐标x的变化关系图线正确的是（     ）

A                 B                 C                   D

分析  设刚开始弹簧的压缩量为x0，即为kx0=mgsinθ。

对于物体B：当弹簧压缩时，

F+k（x0-x）-mgsinθ=ma，

即为F=ma+kx。

当弹簧拉伸时，

F-k（x-x0）-mgsinθ=ma，

即为F=ma+kx。

对于物体A：当弹簧压缩时，

N=mgsinθ+k（x0-x），

即为：N=2mgsinθ-kx。

当弹簧拉伸时，N+k（x-x0）=mgsinθ，

即为：N=2mgsinθ-kx。

综上分析：答案为选项A、D。

点评  解决图像类问题首先应看清楚题目中的横、纵坐标分别代表什么物理量，其次对物体进行受力分析，最后分别对应过程列方程进行求解。该题目从物体B开始运动到物体A离开挡板，弹簧经历了先压缩后拉伸两个过程，因此要对这两个过程分别列方程进行求解，结果发现F和N的规律在这两个过程中都是一样的。

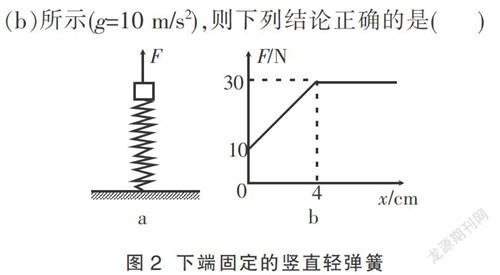
例2  如图2（a）所示，轻质弹簧的下端固定在水平面上，上端放置一小物体（物体与弹簧不连接），初始时物体处于静止状态。现用竖直向上的拉力F作用在物体上，使物体开始向上做匀加速直线运动，拉力F与物体位移x的关系如图2（b）所示（g=10 m/s2），则下列结论正确的是（     ）

A.物体与弹簧分离时，弹簧处于压缩状态

B.物体的质量为3 kg

C.物体的加速度大小为5 m/s2

D.弹簧的劲度系数为7. 5 N/cm

分析  从图像中可以看出当x=4 cm，拉力由变力变为恒力，即小物体只受到拉力F和重力作用，此点就是物体脱离弹簧的临界状态，即为弹簧的原长，A选项错误。脱离时：30-mg=ma（1），拉力刚作用在物体上时：10=ma（2） ，两式联立可得：m=2 kg，a=5 m/s2，B选项错误，C选项正确。拉力没施加前，弹簧处于压缩状态，压缩量为x=4 cm，mg=kx可得k=5 N/cm，D选项错误。综上分析：答案为C。

点评 此题的突破口在于找到x=4 cm时拉力由变力变为恒力，即小物体脱离弹簧的临界状态。

题型2：F-θ图

例  如图3所示，在水平板左端有一固定挡板，挡板上连接一轻质弹簧，紧贴弹簧放一质量为m的滑块，此时弹簧处于自然长度。已知滑块与板间滑动摩擦因数μ=，可认为最大静摩擦力与滑动摩擦力相等。现将板的右端缓慢抬起使板与水平面间的夹角为θ，最后直到板竖直。此过程中弹簧弹力的大小F随夹角θ的变化规律可能是下图中的（     ）

A                                        B

C                                        D

分析  设板与水平面的夹角为θ，滑块相对于板刚要滑动，则mgsinθ=μmgcosθ，得tanθ=μ即θ=，因此θ在0～范围内，弹簧处于原长弹力F=0，当板与水平面的夹角大于时，滑块相对板缓慢滑动，由平衡条件得F=mgsinθ-μmgcosθ=sin（θ-），说明F与θ成正弦形式的关系，当θ=，F=mg，因此C答案正确。

点评  此题的突破口在于随着θ的增加，物体刚要发生滑动的临界状态为：mgsinθ=μmgcosθ，得tanθ=μ，在这之前F=0，之后滑块相对板缓慢滑动，列出平衡条件既可解决此题。

题型3：v-t图

例  如图4（a）所示，一轻质弹簧的下端固定在水平面上，上端叠放两个质量均为M的物体A、B（B物体与弹簧连接），弹簧的劲度系数为k，初始时物体处于静止状态。现用竖直向上的拉力F作用在物体A上，使物体A开始向上做加速度为a的匀加速运动，测得两个物体的v-t图像如图4（b）所示（重力加速度为g），则（     ）

A.施加外力前，弹簧的形变量为 2Mg/k

B.外力施加的瞬间，AB间的弹力大小为M（g-a）

C.AB在t1时刻分离，此时弹簧弹力恰好为零

D.弹簧恢复到原长时，物体B的速度达到最大值

a                          b

分析  施加外力前：2Mg=kx0即x0=2Mg/k，即A答案正确，对AB整体法：F=2Ma（1），隔离A：F-Mg+FBA=Ma （2） 由（1）（2）联立可得FBA=M（g-a）即B答案正确。AB脱离的临界条件是vA=vB，aA=aB，从图中可以看出t1时刻AB脱离，此时对于B，kx-Mg=Ma，可见弹簧仍处于压缩状态，因此C答案错误。此后由于弹力大于重力，B做加速度越来越小的加速运动，当满足弹力等于重力时（图中t2），速度达到最大。t2后重力大于弹力，根据公式Mg-kx=Ma 随着压缩量x的减小，物体做加速度越来越大的减速运动，因此弹簧恢复到原长时速度不是最大值。综上分析：答案为A、B选项。

点评  此题的突破口在于AB脱离的临界条件是vA=vB，aA=aB，即为图中的t1时刻，此时物体B有向上的加速度，弹簧仍处于压缩状态。

题型4： v-x图

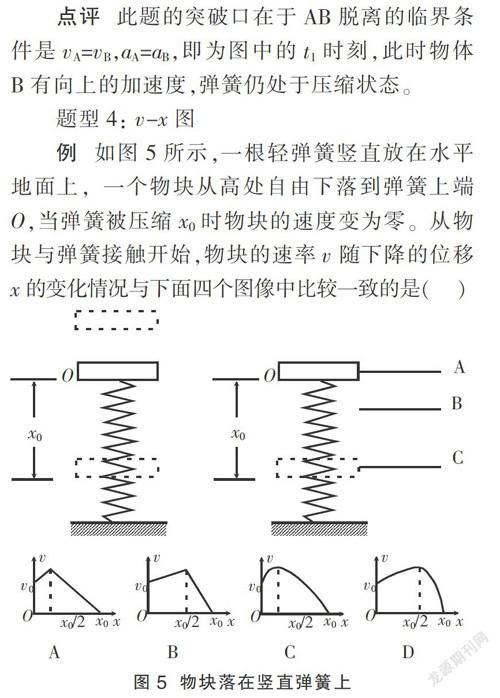
例  如图5所示，一根轻弹簧竖直放在水平地面上，一个物块从高处自由下落到弹簧上端O，当弹簧被压缩x0时物块的速度变为零。从物块与弹簧接触开始，物块的速率v随下降的位移x的变化情况与下面四个图像中比较一致的是（    ）

A                 B                 C                 D

分析  设刚接触弹簧为A点，弹力等于重力的点为B，最低点为C。

物块和弹簧接触后的下落运动是先做加速度减小的加速运动（AB段），然后做加速度增大的减速运动（BC段），物块在B点获得最大速度。物块从A运动到C，根据简谐运动的对称性可知，AB

点评：此题突破口在于物块接触弹簧到运动到最低点经历先加速后减速的过程，此过程可以看作简谐运动，再根据简谐运动的对称性就可以解决。

题型5：a-x图

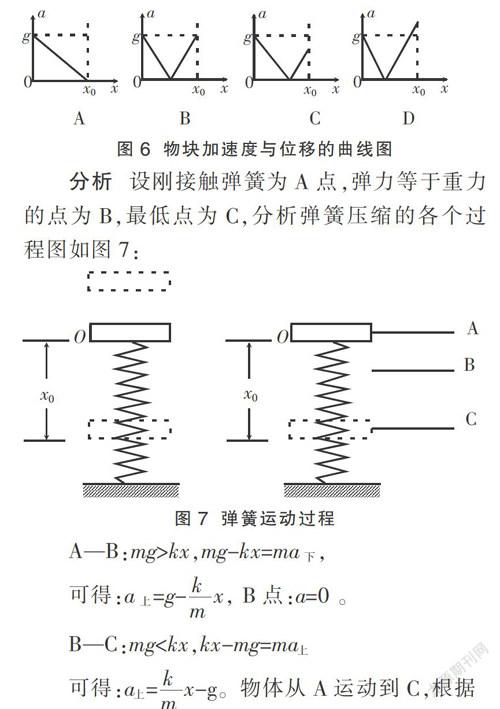
例  如题型4例题情形，一根轻弹簧竖直直立在水平面上，下端固定。在弹簧正上方有一个物块从高处自由下落到弹簧上端O，将弹簧压缩。当弹簧被压缩了x0时，物块的速度减小到零。从物块和弹簧接触开始到物块速度减小到零过程中，物块的加速度大小a随下降位移大小x变化的图像，可能是图6中的（     ）

A               B                   C             D

分析  设刚接触弹簧为A点，弹力等于重力的点为B，最低点为C，分析弹簧压缩的各个过程图如图7：

A—B：mg>kx，mg-kx=ma下，

可得：a上=g-x， B点：a=0 。

B—C：mg

可得：a上=x-g。物体从A运动到C，根据

简谐运动对称性可知，AB

点评  物体接触弹簧到运动到最低点经历先加速后减速的过程，因此对这两个过程分别求出加速度的表达式，再根据简谐运动的对称性就可以解决。

题型6：a-t图

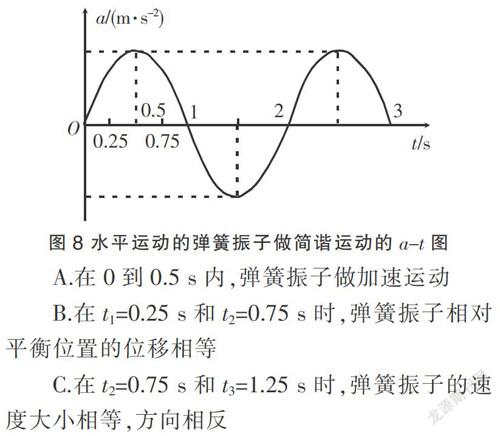
例  一水平弹簧振子做简谐运动，它的加速度a随时间t变化的图线为正弦曲线，如图8所示。下列说法正确的是（ ）

A.在0到0.5 s内，弹簧振子做加速运动

B.在t1=0.25 s和t2=0.75 s时，弹簧振子相对平衡位置的位移相等

C.在t2=0.75 s和t3=1.25 s时，弹簧振子的速度大小相等，方向相反

D.在0到1 s内，t=0.5 s时刻弹簧振子回复力的功率最大

分析：振子在0到0.5 s间，加速度明显增加在远离平衡位置，即在做减速运动，A选项错误。很容易看出B选项正确。t2=0.5 s到t3=1.5 s间物体速度从0先增大后减小到0，根据简谐运动对称性t2=0.75 s和t3=1.25 s时速度大小相等，方向相同，因此C选项错误。功率P=Fv，t=0.5 s时虽然F最大但是v=0，可见P=0，因此D选项错误。综合分析：答案为B选项。

点评  解决此题的关键是题中的已知条件：水平弹簧振子做简谐运动，只要知道振子在做简谐运动，此题的突破口就找到了。

题型7：EK–x图

本题探究的是EK–h，可以看作是EK–x图。

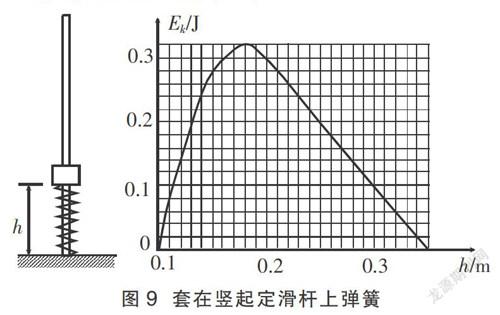
例  如图9所示，竖直光滑杆固定不动，套在杆上的弹簧下端固定，将套在杆上的滑块向下压缩弹簧至离地高度h=0.1 m处，滑块与弹簧不拴接。现由静止释放滑块，通过传感器测量到滑块的速度和离地高度h并作出滑块的Ek-h图像，其中高度从0.2 m上升到0.35 m范围内图像为直线，其余部分为曲线，以地面为零势能面，取g=10 m/s2，由图像可知（    ）

A.小滑块的质量为0.1 kg

B.轻弹簧原长为0.2 m

C.弹簧的最大弹性势能为0.5 J

D.小滑块的重力势能与弹簧的弹性势能总和最小为0.4 J

分析  在EK-h图像中，图线的斜率表示滑块所受的合外力，由于高度从0.2 m上升到0.35 m范围内图像为直线，其余部分为曲线，说明滑块从0.2 m处上升到0.35 m所受作用力为恒力。可见0.2 m，滑块与弹簧分离，故B选项正确。从0.2 m处上升到0.35 m，图线的斜率绝对值为：k=mg=2 N，所以m=0.2 kg，故A选项错误。 根据能量的转化与守恒可知，当滑块上升至最大高度时，增加的重力势能即为弹簧最大弹性势能，所以Epm=mg△h=0.2×10×（0.35-0.1）=0.5 J，故C选项正确。在滑块整个运动过程中，系统的动能、重力势能和弹性势能之间相互转化，因此动能最大时，滑块的重力势能与弹簧的弹性势能总和最小，系统总的机械能为：E总=E弹max+mgh=0.7 J，滑块的动能最大为0.32 J，因此小滑块的重力势能与弹簧的弹性势能总和最小为0.38 J，因此D选项错误。综上分析：答案为B、C选项。

点评  此题的突破口在于：高度0.2 m～0.35 m的图像为直线，EK-h图中图线的斜率表示滑块所受的合外力，根据0.2 m～0.35 m这段的斜率就可以求出质量。0.2 m处滑块脱离弹簧，因此弹簧处于原长。这两点找到了，此题就容易突破了。

题型8：混合型图

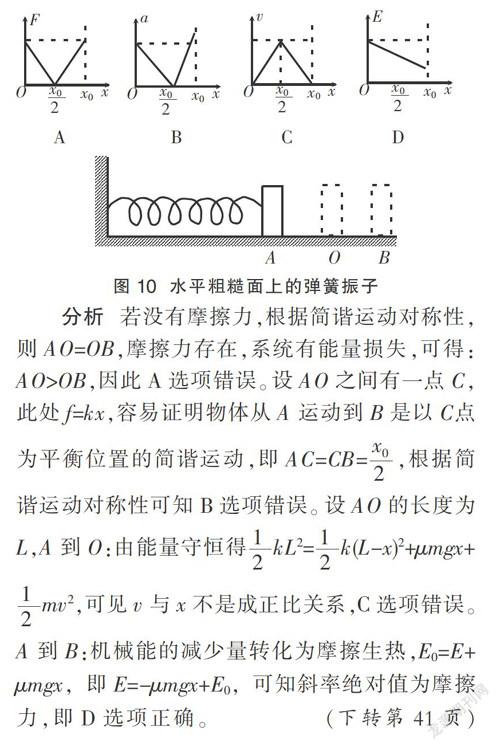
例1  如图10所示，一根轻弹簧左端固定，右端系一物块，物块置于摩擦不能忽略的水平面上。现将弹簧压缩到A点后释放，物块运动到B点时速度变为零，O为弹簧处于自然长度时的位置，AB距离为x0。物块从A到B的过程中，弹簧弹力的大小F、物块加速度的大小a、物块速度的大小v、物块和弹簧组成的系统机械能E随物块的位移x变化的图像可能是（     ）

A                 B                C                D

分析  若没有摩擦力，根据简谐运动对称性，则AO=OB，摩擦力存在，系统有能量损失，可得：AO>OB，因此A选项错误。设AO之间有一点C，此处f=kx，容易证明物体从A运动到B是以C点为平衡位置的简谐运动，即AC=CB=，根据简谐运动对称性可知B选项错误。设AO的长度为L，A到O：由能量守恒得kL2=k（L-x）2+μmgx+mv2，可见v与x不是成正比关系，C选项错误。A到B：机械能的减少量转化为摩擦生热，E0=E+μmgx，即E=-μmgx+E0，可知斜率绝对值为摩擦力，即D选项正确。

点评  此题的突破口是物体从A运动到B是以C点为平衡位置的简谐运动，即AC=CB=。抓住这点再根据简谐运动的对称性就可以解决此题。

例2   如图11所示，水平面绝缘且光滑，一绝缘的轻弹簧左端固定，右端有一带正电荷的小球，小球与弹簧不相连，空间存在着水平向左的匀强电场，带电小球在电场力和弹簧弹力的作用下静止，现保持电场强度的大小不变，突然将电场反向，若将此时作为计时起点，则下列描述速度与时间、加速度与位移之间变化关系的图像正确的是（   ）

A                 B                 C                 D

分析  电场反向后：qE+kx=ma，

即a=x+，

随着x的减小，物体在做加速度越来越小的加速运动，当物体运动到弹簧原长时x=0，a=，此后做匀加速直线运动，因此A、C选项正确。

点评  此题的突破口在于物体在弹簧原长时脱离，脱离时物体受到的合外力为F=qE，此后保持不变。

综上所述：针对弹簧中的图像问题，要能分析有关图像所表达的物理意义，抓住图像的斜率、截距、交点、临界点等几个要点，常常就可以方便、简明、快捷地解决此类问题。

参考文献：

[1]路天明.对一道双平衡位置振动问题的讨论[J].物理通报，2011（10）：92.

[2]高正球.高考中弹簧类问题分析[J].物理教学探讨，2008，26（11）：5—6.

[3]叶正勇.谈弹簧的弹力与弹性势能[J].物理教师，2015，36（1）：56—59.

[4]熊翠华.利用弹簧的特点解决疑难问题[J].中学物理，2013，31（12）：82—83.

（栏目编辑  罗琬华）