思维的广度、梯度和深度
2015-10-27陈信余
陈信余





摘 要:本文以一道具体的测试题为例,在分析试题特点的基础上,结合部分学生的答题情况,对思维的广度、梯度和深度与学生的能力层次做了简要的分析,强调在物理教学中要重视思维层次、培养思维能力,提出思维能力培养可以通过“讨论与判断”问题的方式来实现。
关键词:思维;广度;梯度;深度
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2015)9-0028-3
分析、综合、比较以及抽象、概括等既是思维活动的基本过程,又是思维活动的基本方法。考查学生解决或处理物理问题能力的试题,其着力点往往会落在思维的过程和方法上。而思维的广度、梯度和深度则是这个过程和方法的具体表现。现以2015广州市理科综合(物理)测试第36题为例,在分析试题特点的基础上,结合部分学生的答题情况,对思维的广度、梯度和深度与学生的能力层次做简要分析,为思维能力培养的方法和途径提供参考。
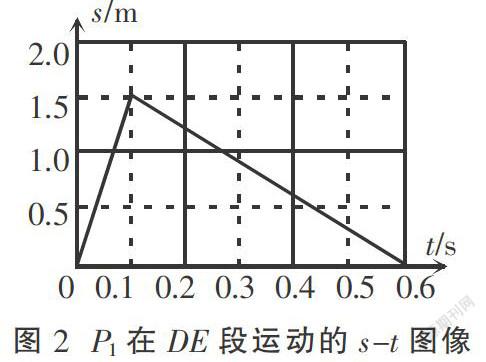
案例1 如图1,轨道固定在竖直平面内,水平段DE光滑、EF粗糙,EF上有一竖直挡板, ABCD光滑并与水平段平滑连接,ABC是以O为圆心的圆弧,B为圆弧最高点。物块P2静止于E处,滑块P1从D点开始水平向右运动并与P2发生碰撞,且碰撞时间极短。
已知:P1的质量m1=0.5 kg,与P2碰撞前后的位移图像如图2。P2的质量m2=1.8 kg,与EF轨道之间的动摩擦因数μ=,与挡板碰撞时无机械能损失。圆弧半径R= m,P1、P2可视为质点且运动紧贴轨道。(取g=10 m/s2)
求:(1)P2被碰后获得的速度大小?
(2)P1经过B时受到的支持力大小?
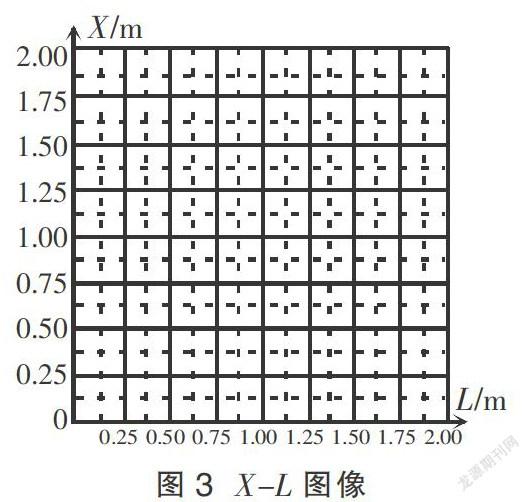
(3)用L表示挡板与E的水平距离。若P2最终停在了EF段距离E为X的某处,试通过分析与计算,在图3中作出X-L图线。
1 试题特点的分析
1.试题设置了一个较真实的情境,物体在水平面内和竖直面内运动,涉及直线运动和曲线运动。2.涉及较多的知识点,主要包括s-t图像、匀速直线运动、匀变速直线运动、动量守恒定律、圆周运动、机械能守恒定律、牛顿运动定律。3.信息量大,有文字信息、图片信息、图像信息。4.过程往复,P1向右运动,与P2碰撞后向左运动,冲上圆弧后离开。P2被P1碰撞后向右运动,碰挡板后又向左运动,冲上圆弧后返回水平面又向右运动。5.思维周密、严谨,而且有层次、有梯度和深度。P2最终停在EF段的情况有多种可能性,一种是直接减速到停下来;第二种是与挡板碰撞后返弹减速到停下来;第三种是返弹经过E处后进入DE段再冲上圆弧又返回到水平段向右减速到停下来,其中这里面还要判断与挡板是否有多次碰撞,思维深度要求很高。6.数学要求比较全面,主要涉及基本的运算和推断、识图、用图和作图、分段函数的表达与作图。
2 思维层面的考查
试题的第(1)(2)问考查的是比较基本的、常规的物理知识,对思维能力要求不高。下面结合学生答题重点就第(3)问做简要的评析。
2.1 思维的广度
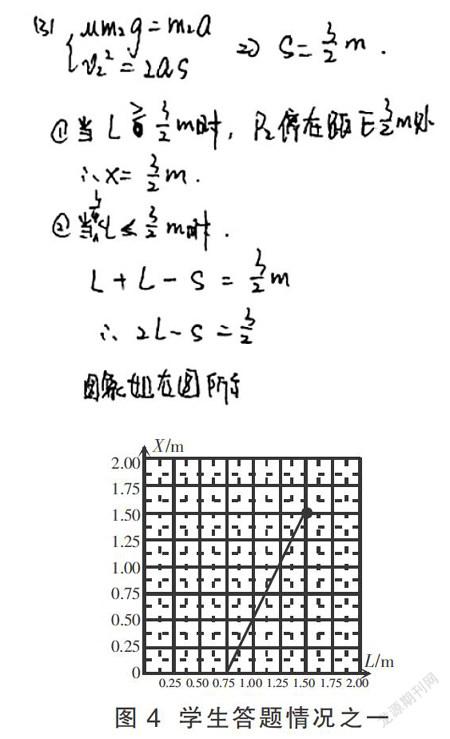
思维广度是指在同一思维层面上,对影响、制约问题的各种可能因素有一个大致的认识。各因素之间没有递进和深浅的并列关系,讲究思维的发散度,如简单的分类和事实罗列之类。此类思维层次学生的答题情况如图4。
对学生来说,解答物理问题就是一种认识过程。从该类学生的答题来看,学生没有从具体的现象、条件出发,运用相关知识,由此及彼、由表及里地揭示该题中存在的物理现象及内在联系,实现从认识表面现象到认识内在本质及其联系的转变。学生只认识到挡板距E的距离L≥1.5 m和L<1.5 m时,P2停在EF段的两种可能情况,至于为什么要0.75≤L这个条件,没有在这个解题中留下思维痕迹,反映出学生条件意识的缺乏。由于没有从已有条件出发,对P2停在EF段有两种可能情况的确立,在思维层面上属于同一层次的,没有梯度。而且思维广度也不够,因为第三种停在EF段的可能情况没有反映出来。
2.2 思维的梯度
思维梯度是在思维广度的基础上,不仅能找出影响、制约问题的各种因素,而且还能将各种因素的逻辑关系理顺,各因素之间有层层递进的关系,讲究的是思维的周密性。在具体处理问题时,往往表现为有条件意识,能充分考虑到已知条件的作用与限制,在已有的条件下分析与讨论问题。这类思维层次学生的答题情况如图5。
可以看出,该类学生的思维层次比上一类学生明显有提高。对P2能停在EF段的各种可能情况做了全面的考虑,并对其中几种可能情况的相应条件也做了比较清楚的表述。但思维的深度仍有欠缺。学生分析论证了当L<0.75 m时,P2总能返回到EF上来。但对L<0.5 m时P2有可能冲出轨道的情况没有考虑周全,反映出学生思维的严谨性不够。从思维方法上来看,学生采用的是分析法而不是综合法,即把事物的整体分解成若干个部分来考虑,而不是把事物的各个部分、各种特性联系起来从整体上考虑。本试题中P2与挡板碰后能停在EF段的条件是:P2不会从弯曲轨道飞出。设此时挡板距E的距离为L1,即:m2v-μm2g·2L1
2.3 思维的深度
思维的深度是指在纵横两个纬度对问题的全面思考,讲究的是思维的严谨性。在处理具体问题时,往往表现为不仅仅能充分应用已有的条件,而且还能挖掘隐含条件,在分析、比较的基础上,还会对一些特殊情况做出必要的判断。这类思维层次学生的答题情况如图6。
从答题情况来看,这类学生的思维严谨程度显然比前面两类学生要高,反映出该类学生具备一定的思维深度。对控制P2最终能停在EF段的因素有清楚的认识:挡板到E的距离L、曲面的高度和P2向左运动经过E的速度大小。在这个大前提下又对各种情况做了比较详细的分析,对每一种情况都有逻辑推理和分析,层层递进,且每一种可能情况也都有对应的条件,思维比较周密、严谨。对L<0.5 m时,P2会从B点冲出这一隐含条件挖掘出来了,并做了判断和说明,显然思维的广度、梯度和深度很明显地展现出来了。但该类学生的思维深度也没有达到最高状态,对P2返回EF后,是否与挡板存在多次碰撞的问题,没有留下任何思维痕迹(虽然作图没有问题,但分析与计算中没有反映这一点),也许学生根本就没有考虑或发现这个问题,或者想当然地认为只发生了一次碰撞。而这个问题必须做出判断,否则,L在0.5~0.7 m之间还有其他可能情况出现。判断是对思维对象是否存在、是否具有某种属性以及事物之间是否具有某种关系的肯定或否定。判断是思维活动中最基本的过程,也是最基本的方法,往往要结合具体的情境,充分利用已有的条件,进行分析、综合和比较。本题在确定P2最终停在EF段的条件是L≥0.5 m后,可以通过假设或比较判断来确定P2与挡板发生碰撞的次数。设挡板距E的距离为L1≥0.5时,P2与挡板能碰N次,此时满足:mv>μmg·(2N-1)L,求出N的具体值。或者通过能量比较:mv≤3μmg·L来确定碰撞的次数。该问题可以考查学生思维的周密、细致和严谨,把学生的能力层次区分出来。
3 思维层次与能力
从以上的分析可以看出,学生处理或解决物理问题的能力,往往可以通过思维层次来体现。因此,在物理教学中重视思维层次,培养思维能力就显得尤为重要。
培养思维能力的方法和途径多种多样,其中通过“讨论与判断”问题的训练是一种不错的选择。“讨论”涉及到分类,可以保证思维广度这个层面的训练;“讨论”容易诱发新的问题,这可以让思维的梯度得到训练;“判断”是推理的最基本的思维形式。推理就是根据一个或几个已有的判断得出一个新判断的思维形式。因此,“判断”可以确保思维深度的训练。
讨论与判断问题对学生独立分析问题的能力和思维周密性、严谨性要求较高,因为任何物理问题都是由物理情境和条件组成的,物理情境和条件发生变化,必然会使物理现象和相应结果发生变化。对在什么条件下遵循什么样的物理规律、在什么情境下发生什么样的物理现象,必须全面考虑。另外经数学处理后得到的结果,在物理上是否合理、是否合乎实际以及所得结果的物理意义如何,都需要进行讨论和判断,这既是一种能力,也是一种科学态度。
参考文献:
[1]袁守华.物理解题思维的理论和方法[M].北京:北京师范大学出版社,2011.(栏目编辑 李富强)