Weitjenbock不等式证明的再探究

吴启斌，刘红艳，李雪婷，席维鸽，李鑫瑞

（1.咸阳师范学院数学与信息科学学院，陕西咸阳712000；2.铜川市耀州区庙湾中学，陕西铜川727102）

Weitjenbock不等式证明的再探究

吴启斌1，刘红艳2，李雪婷1，席维鸽1，李鑫瑞1

（1.咸阳师范学院数学与信息科学学院，陕西咸阳712000；2.铜川市耀州区庙湾中学，陕西铜川727102）

Weitjenbock不等式是一个典型的用代数方法证明几何不等式，自从1919年几何学家Weitjenbock给出这个著名的不等式并于1961年选为第三届国际奥林匹克试题，近百年来在数学界引起了极大的研究热情并给出了许多不同的证明方法。论文给出Weitjenbock不等式的5种多向思维新的证明方法，用三角的方法给出Finsler加强结果的一个新证明，进一步给出Weitjenbock不等式发散的几个新的证明。

Weitjenbock不等式；Finsler加强；发散

文献［1-2］给出Weitjenbock不等式的证明、推广、发散及Finsler加强结果，并把Weitjenbock不等式和Finsler加强结果推广到n边形，文献［3-4］介绍了Finsler加强结果并从纯几何的角度证明了Finsler加强结果，文献［4-6］介绍了Weitjenbock不等式及推论的多向思维证明。本文在此基础上给出Weitjenbock不等式的一些新的证明方法，并用三角的方法给出Finsler加强结果的一个新证明。

1　Weitjenbock不等式的几种新的证明方法

定理1设a，b，c分别为三角形三边之长，S为其面积，则有a2+b2+c2≥4S。

（当且仅当a=b=c时等号成立）。

证法1：利用秦九韶——海伦公式证明。

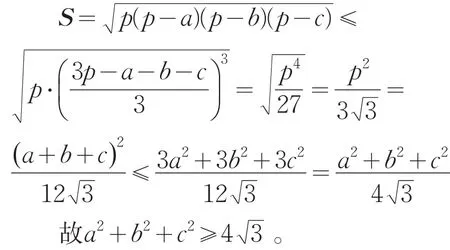
证法2：记∠A对应边BC的高为ha，中线为ma，BC的中点为D，在△ABC和△ABD中由余弦定理

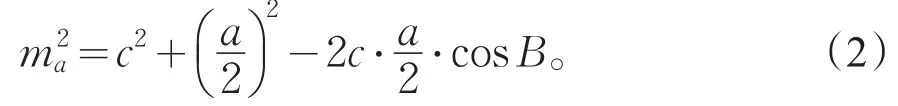
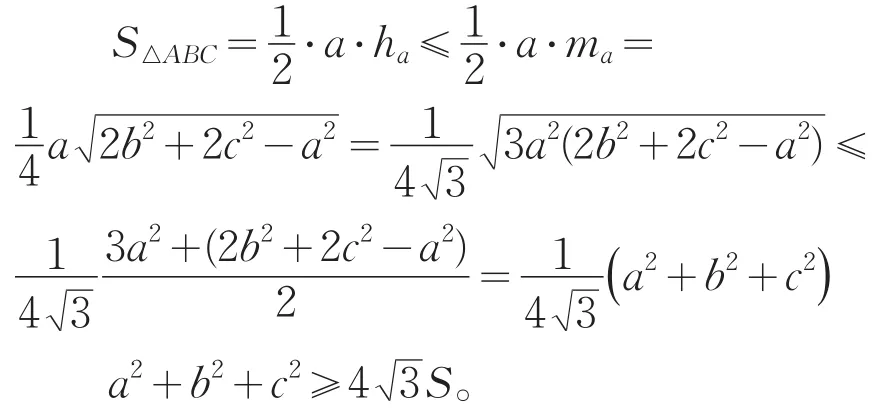
证法3：因为在周长一定的三角形中，正三角形的面积最大，设周长为a+b+c的正三角形的面积为S′，则

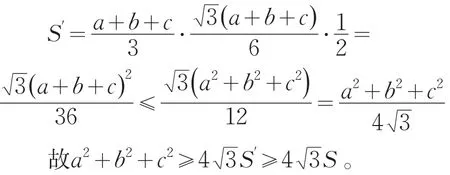
证法4：利用分析法证明

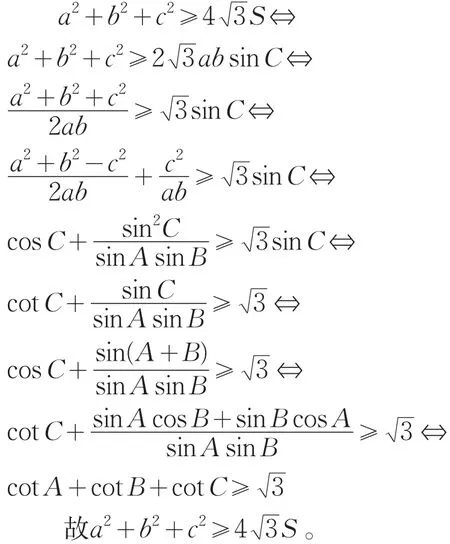
证法5：利用△ABC中

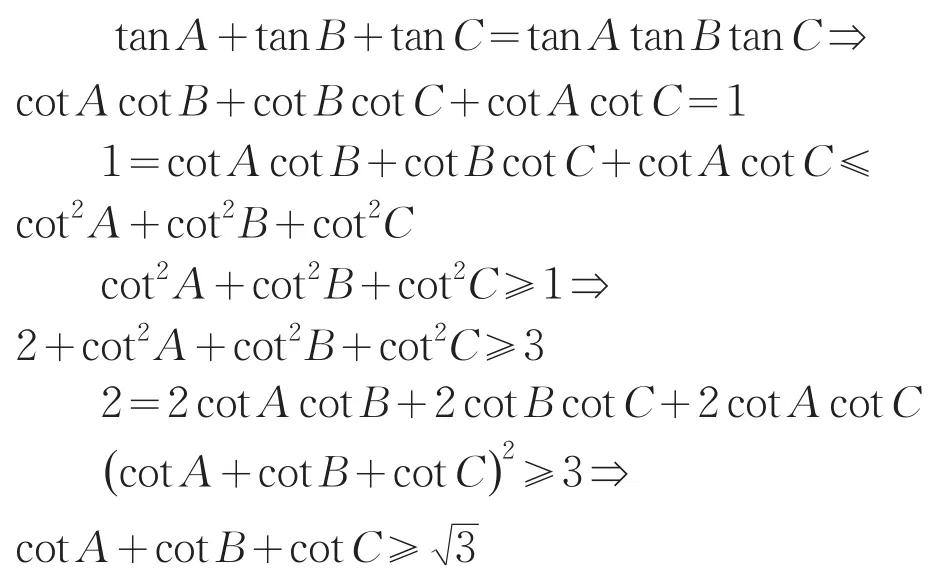
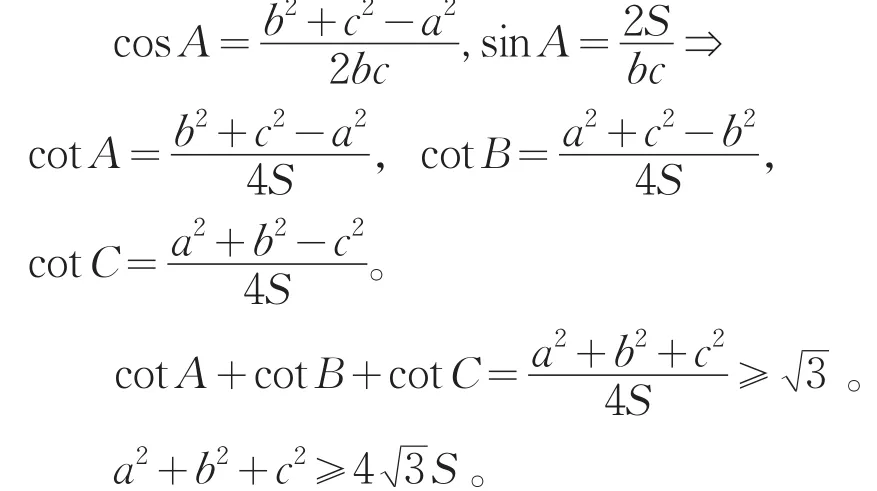
2　Finsler的加强结果的新证法

1938年著名几何学家Finsler用几何的方法给出了Weitjenbock不等式的加强结果。设a，b，c分别为三角形三边之长，S为其面积，则有

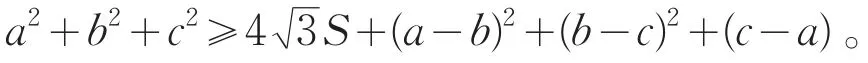
现在给出一种新的证明方法。

证明：在△ABC中有

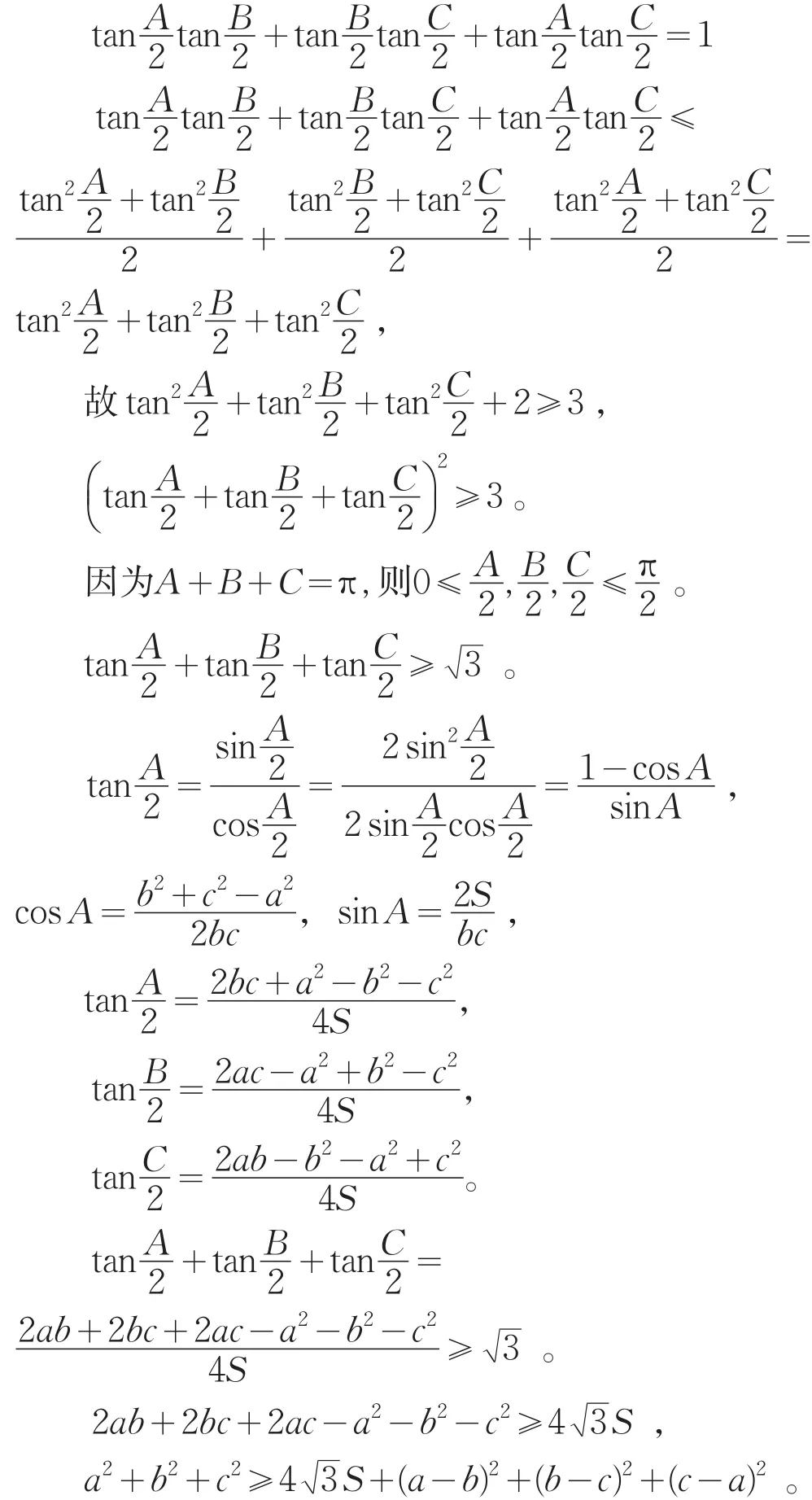
3　Weitjenbock不等式的推论

推论1设a，b，c分别为三角形三边之长，S为其面积，则有ab+bc+ac≥。当且仅当a=b=c时等号成立。

推论2设a，b，c分别为三角形三边之长，S为其面积，则有，当且仅当a=b=c时等号成立。

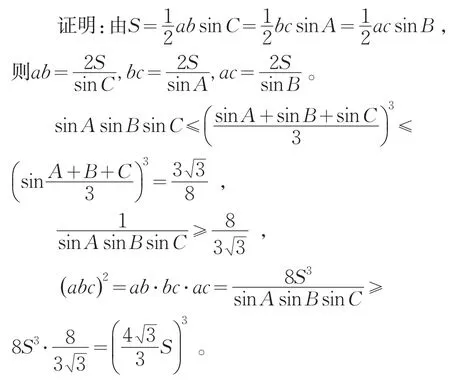
推论3设△ABC与△A'B'C'的三边及面积分别为a，b，c，s与a'，b，'c'，s，'则a2a′2+b2b′2+c2c′2≥16SS′，当且仅当a=b=c时等号成立。

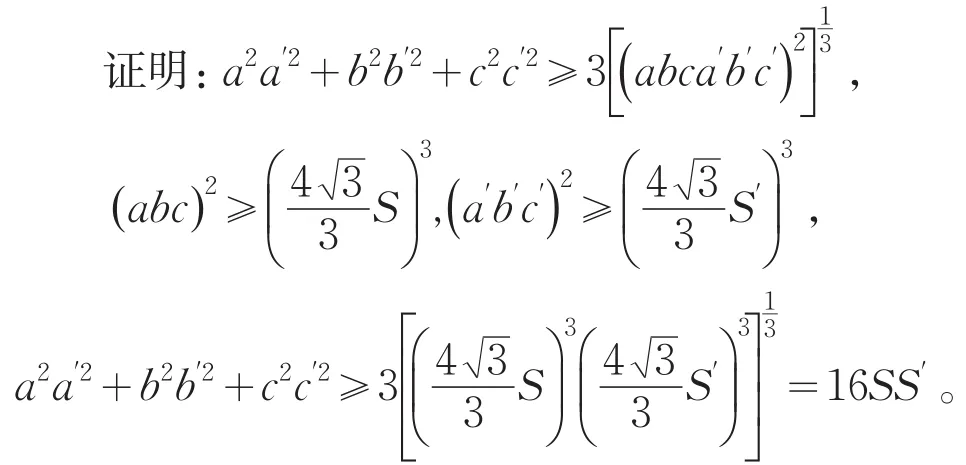
4　结论

从对Weitjenbock不等式的研究可以看出几何不等式涉及的内容非常丰富，处理问题的方法与技巧灵活多变，往往与三角、代数等知识有密切的联系，因而历来是数学奥林匹克热点之一。因此，抓住几何图形的特征，挖掘其中所蕴含的基本几何不等关系，常常是解决几何不等式的重要方法。教学中通过引导学生对Weitjenbock不等式的多向思维证明的研究，有利于培养学生的发散思维和创新能力，有利于提高学生发现问题、分析问题和解决问题的能力。

［1］吴启斌.Weitjenbock不等式的证明与推广［J］.咸阳师范学院学报，2005，20（6）:13-15.

［2］吴启斌.Finsier不等式的证明与推广［J］.中学数学教学参考，1998（10）:38.

［3］朱恩宽.初等几何教程［M］.西安:陕西师范大学出版社，1991:204-205.

［4］张奠宙，张广祥.中学几何研究［M］.北京:高等教育出版社，2005:71-72.

［5］任璋辉.数学思维理论［M］.南宁:广西教育出版社，2001: 216-219.

［6］陈传理，张同君.竞赛数学教程［M］.北京:高等教育出版社，2013:220-221.

Exploration on the Demonstration of Weitjenbock Inequality

WU Qibin1，LIU Hongyan2，LI Xueting1，XI Weige1，LI Xinrui1
（1.School of Mathematics and Information Science，Xianyang Normal University，Xianyang 712000，Shaanxi，China；2.Miaowan Middle School，Yaozhou District，Tongchuan 727102，Shaanxi，China）

Weitjenbock inequality is a typical geometric inequality of algebraic method to prove. Since 1919，the famous inequality was given by Weitjenbock，and it was chosen as the Third International Olympic Games in 1961.In the last hundred years，it has aroused great enthusiasm in the field of mathematics and gave a lot of different methods to prove it.The main purpose of this paper is to use the elementary method o propose some new different methods on the proof of Weitjenbock inequality in muti-direction thinking and to put forward a new mean over the proof of Finler strengthen result.Furthmore，some new proofs about Weitjenbock inequality were raised as well.

Weitjenbock inequality；Finsler strenthen；divergency

O122.3

A

1672-2914（2015）06-0051-03

2015-04-10

吴启斌（1956-），男，陕西乾县人，咸阳师范学院数学与信息科学学院教授，研究方向为数学教学论和数学竞赛。