基于多分类支持向量机的船舶桨叶数识别研究
2015-10-26戴卫国邱家兴王易川程玉胜
戴卫国† 邱家兴 王易川 程玉胜
(海军潜艇学院 青岛 266042)
⋄研究报告⋄
基于多分类支持向量机的船舶桨叶数识别研究
戴卫国†邱家兴王易川程玉胜
(海军潜艇学院青岛266042)
分析了目前常用的支持向量机多分类方法以及存在的不足,本文提出了一种混合纠错输出编码的多分类支持向量机改进算法,并应用于利用船舶目标辐射噪声DEMON谱进行船舶桨叶数分类的实验。理论分析与实验结果表明,该改进算法编码明确、具备纠错能力,是一种有效的多分类支持向量机方法,在船舶桨叶数识别中,其分类性能优于一对余、一对一及最小输出编码支持向量机等多分类方法,可适用于船舶桨叶数的分类识别。
船舶辐射噪声,支持向量机,多分类,螺旋桨桨叶数
1 引言
船舶目标桨叶数物理意义明确,与船舶工况无相关性,是进行水声目标识别最重要的识别特征之一,在某些情况下单凭桨叶数即可识别目标,这对船舶目标识别具有特别的意义。通过对船舶辐射噪声的DEMON(Detection of envelope modulation on noise)谱分析可以获取船舶目标桨叶数特征[1]。
支持向量机(SVM)是一种基于统计学习理论的模式识别方法,建立在统计学习理论VC维(Vapnik Chervonenkis dimension)理论和结构风险最小原理基础上,采用结构风险最小化原则代替了传统机器学习方法中的经验风险最小化原则,与其他学习机相比具有良好的推广能力和很强的普适性,已经被成功地应用到目标识别与分类等问题中[2-4]。但是,传统的SVM是基于两类目标分类问题,而实际需要解决的一般是多类问题,如何有效地将其推广到多类问题仍是当前SVM研究的重要内容之
一[5-6]。
本文通过对目前SVM分类方法的分析,在纠错输出编码(Error correcting out code,ECOC)SVM多分类的基础上,克服纠错输出编码的编码随机的不足,以一对余、一对一的多分类方法为基础,将稠密型和稀疏型纠错输出编码方法融合在一起,提出了一种混合纠错输出编码(MECOC)SVM多分类算法,该算法编码明确、具备纠错能力。通过利用船舶目标辐射噪声DEMON谱进行螺旋桨桨叶数分类的实验,表明该算法是一种有效的SVM多分类方法。
2 传统的SVM多分类方法
目前通常使用的SVM多分类方法主要有用多个两类分类器实现、用层次型两类分类器实现、用一个最优化问题一次性实现和用纠错输出编码实现等方法[5-7]。
2.1用多个两类分类器实现多类分类
用多个两类分类器实现多类分类的方法主要有一对余、一对一两种方式。
2.1.1一对余
“一类对余类(One-versus-all,简称一对余)”算法是SVM解决多分类问题的一种方法,对于k(k≥2)类分类问题,构造k个两类分类器,将k分类问题转化为k个两类分类问题。第i个SVM分类问题是把第i类作为一类,其余k-1类为另一类。对于给定的l个训练样本(x1,y1),···,(xl,yl),j,j=1,2,···,l,yj∈{1,...,k},第i个SVM可通过求解下面的最优化问题得到
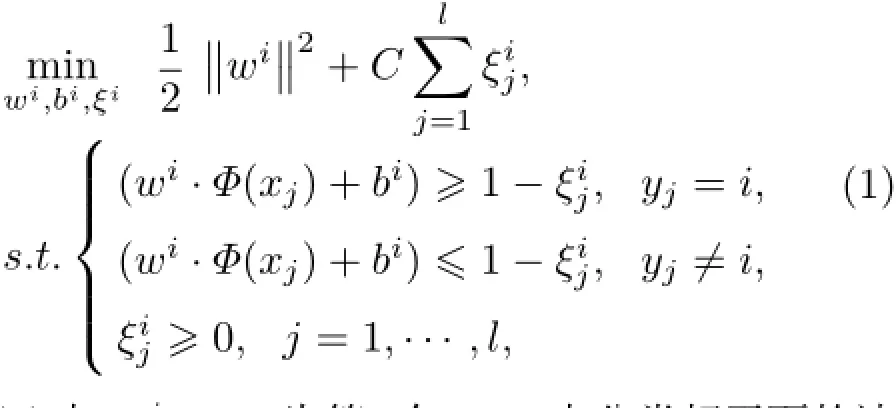
式(1)中:wi∈Rn为第i个SVM中分类超平面的法向量;bi∈R为偏置量;ξj∈R为约束条件中非负的松弛项;C为惩罚因子;Φ是所采用的核函数。
对未知样本x进行分类时,用k个两类决策函数进行判定,x属于wi·Φ(x)+bi中最大值的上标i所对应的类别[6-7]。
2.1.2一对一
“一类对一类(One-versus-one,简称一对一)”算法是SVM解决多分类问题的另一种方法,该算法是在每2类之间训练一个SVM分类器,因此对于一个k类问题,训练阶段共构造k(k-1)/2个两类分类器,每个分类器是取任意2个类别的数据进行训练。对第i类和第j类之间的分类器,可通过求解下面的最优化问题得到

对未知样本x进行分类时,常用的一种方法是“最大投票法”,x属于最后票数最多的那一类[7]。
2.2用纠错输出编码实现多类分类
2.2.1纠错输出编码
纠错输出编码SVM分类方法是对类别通过二进制编码将多类问题转化为多个两类问题,采用具有纠错能力的编码对类别进行编码,并将SVM作为码位分类器的一种多分类算法。
对于k类数据的分类问题,定义一个k×m的编码矩阵M,每一行称为“码字”,每一个编码元素称为“码位”,每个元素的取值范围可采用二符号{-1,+1}表示,“1”和“-1”表示正、负两类(即稠密型编码),或采用三符号{-1,0,+1}表示,“0”表示该码字位所对应的类不参加该分类器的训练(即稀疏型编码),这就把k类分类问题转化为m个两类分类问题。由于每个码位上的分类器只需要做两类分类,所以可以采用SVM作为码位分类器。
对于一个新样本,m个SVM分类结果构成一个码字S,k个编码中与S汉明距离最小的码字所代表的类别就是这个新样本所属类别。对于一个最小汉明距离为d的编码来说,最少能修正(d-1)/2位错误[8-9]。
2.2.2最小输出编码
最小输出编码(MOC)是在纠错输出编码方法基础上进行的一种改进方法,而改进的重点就是采用确定的最少的两类支持向量机实现多类分类。在二进制数的基础上构建分类编码矩阵,建立采用能够对多类问题进行分类的最小数目的两类分类器。其中,四类分类问题只需要两个二类分类器即可构造分类编码矩阵。但该编码的最小汉明距离为2,不具备纠错能力[10]。
2.2.3最小汉明距离译码
在译码过程中,一般采用最小汉明距离译码的方式进行译码,在编码过程中存在稀疏编码的情况下,即在{-1,0,1}三符号编码情况下,两向量U,V∈{-1,0,1}l之间的汉明距离为[8]

其中,l为编码长度。
3 混合纠错输出编码SVM多分类方法
3.1传统SVM多分类存在的主要问题
从目前常用的SVM多分类方法来看,主要存在以下问题:
(1)用一个最优化问题一次性实现多类分类,由于需要同时优化选择多个SVM的模型参数,不利于SVM的参数寻优,分类精度一般;
(2)用层次型两类分类器实现多类分类,主要是用有向无环图和二叉树结构多分类SVM进行多分类。由于存在误差积累问题,应用存在一定的局限性;
(3)应用最普遍的一对一、一对余方式用多个两类分类器实现多类分类,但存在误分、拒分区域较大的问题;
(4)最小输出编码不具备纠错能力,且也存在误差积累问题;
(5)常规的纠错输出编码具备(d-1)/2位的纠错能力,但其在编码过程,尤其详尽码(Exhaustive codes)编码[10]时,对实际问题的聚类性质考虑不够,在划分目标类型时,常把不相干的两类及多类目标混成一类目标进行训练,人为地增加了SVM的训练难度和测试误差。
3.2混合纠错输出编码的基础编码
3.2.1一对余编码
一对余的SVM分类方法可以看作是纠错输出编码的一种特殊方式,属于稠密型编码类型(即二符号编码),该方式的编码方式为在每个分类器基中都把对应的类作为正类而把其他作为负类来训练。具体编码形式为

该编码的码间最小汉明距离为2[8],不具备纠错能力。
3.2.2一对一编码
一对一的SVM分类方法仍可以看作是纠错输出编码的一种特殊方式,属于稀疏型编码类型(即三符号编码),所有类两两之间的每一个组合都对应于一个分类器。具体形式为

该编码的码间最小汉明距离为(C2k-1)/2+1[8],在k≥4的情况下,具备纠错能力。
3.3混合纠错输出编码的SVM多分类编码
在纠错输出编码的基础上,以一对余、一对一的多分类SVM为依托,将稠密型和稀疏型纠错输出编码方法融合在一起,提出了一种混合纠错输出编码多类SVM算法。
3.3.1混合纠错输出编码多分类支持向量编码原则
(1)“冗余编码”
按照一对余、一对一的SVM二分类器的原则,分别训练各SVM分类器,并进行各分类器的分类模型寻优。然后将一对余、一对一的所有分类器均参加分类编码,各分类可采用不同的模型参数,不同的核函数和不同类型的SVM算法。
(2)“分区配置”
将一对余配置的各分类器放置于I区,将一对一配置的各分类器放置于II区,两区平行配置。
3.3.2混合纠错输出编码多分类支持向量编码方法
按照3.3.1的编码原则,以“+1”表示将此类目标样本编入正类;以“-1”表示将此类目标样本编入负类;“0”表示将此类样本不参加训练,构建了混合纠错输出编码的编码方法:

该编码的码间最小汉明距离为(C2k-1)/2+3,在多类(k≥3)的情况下,具备(C2k-1)/4+1位的纠错能力。
混合纠错输出编码的理想输出为该编码的编码方案,以四类(A、B、C、D)为例,A类的理想输出编码为{1-1-1-1 1 1 1 0 0 0};B类的理想输出编码为{-1 1-1-1-1 0 0 1 1 0};C类的理想输出编码为{-1-1 1-1 0-1 0-1 0 1};D类的理想输出编码为{-1-1-1 1 0 0-1 0-1-1}。
但在实际的目标译码过程中,A目标在“B对C”、“B对D”、“C对D”的分类判决中,同样会有“+1”或“-1”的输出,不可能先知先觉地输出“0”而到达理想的输出。因此在实际输出中,在3分类混合纠错输出编码到理想输出编码的最小汉明距离为0.5,在4分类混合纠错输出编码到理想输出编码的最小汉明距离为1.5,在5分类混合纠错输出编码到理想输出编码的最小汉明距离为3.0。
3.4混合纠错输出编码最小汉明距离译码算法
(1)按照混合纠错输出编码方案对目标样本进行分组,可分为正类、负类,或不参加训练;
(2)按照分组方案分别训练各二分类SVM分类器,寻求最优分类模型参数,构建支持向量机分类模型;
(3)应用各二分类SVM分类器对待识别目标样本进行分类,输出其分类编码;
(4)分别计算该输出编码与各类理想输出编码之间的汉明距离;
(5)汉明距离最小的类别即为该目标输出类别。
4 实验及分析
4.1实验准备
目前,船舶螺旋桨叶片数一般为三叶、四叶、五叶、六叶和七叶共五类,根据叶片数从三叶到七叶的顺序,可将舰船目标分为A~E五类。
桨叶数识别主要包括特征提取和分类识别两部分。在特征提取部分,通过对船舶目标辐射噪声进行DEMON谱分析,提取DEMON谱轴频的1至15阶谐波线谱的幅度、线谱宽度,轴频的频率稳定度、幅度稳定度,谐波簇信噪比共33维特征,进行归一化处理后作为桨叶数识别的特征;在分类识别部分,为验证本文提出的基于混合纠错输出编码的SVM算法有效性,本文同时采用“最小输出编码SVM”、“一对余SVM”、“一对一SVM”、“BP(Back propagation)神经网络”和“近邻法”共5种分类算法进行桨叶数识别,作为对比参照算法。
进行试验的船舶目标辐射噪声样本全部为海上综合声纳听测波束实际录取的船舶目标噪声,试验样本的选取条件:(1)在综合声纳对噪声目标探测和稳定跟踪后输出得到的远场单目标噪声信号;(2)船舶目标噪声DEMON谱中存在可见的调制线谱;(3)船舶目标的类型特征、桨叶数明确。通过样本选取共获取了3725个船舶目标噪声样本,按叶片数进行分类,其中A类样本1466个、B类样本1101个、C类样本570个、D类样本240个、E类样本348个。
4.2桨叶数识别特征提取
对船舶辐射噪声依次进行带通滤波、检波、低通滤波、降采样、FFT(Fast Fourier transformation)变换得到DEMON谱[1],如图1所示,横坐标为频率,纵坐标为幅度。DEMON谱中一般存在很多频率成倍数关系的谐波线谱,这组谐波中的第一根线谱频率对应螺旋桨转速。根据谐波线谱的幅度关系、宽度特征、稳定度、信噪比等特征,可以判断螺旋桨的桨叶数信息,图1为典型的4叶桨目标DEMON谱图。
本文提取的桨叶数识别特征是由以下5部分特征组成的33维特征矢量:
(1)轴频的1至15阶谐波线谱的归一化幅度大小;
(2)轴频的1至15阶谐波线谱的归一化宽度大小;
(3)轴频的频率稳定性,本文以30 s数据中轴频频率变化的方差作为频率稳定性特征;
(4)轴频的幅度稳定性,本文以30 s数据中轴频幅度变化的方差作为幅度稳定性特征;
(5)谐波簇信噪比,本文以15阶谐波线谱相对背景干扰线谱的突出程度作为信噪比特征。
据此对图1所示DEMON谱进行分析,得到33维桨叶数识别特征矢量如图2所示。
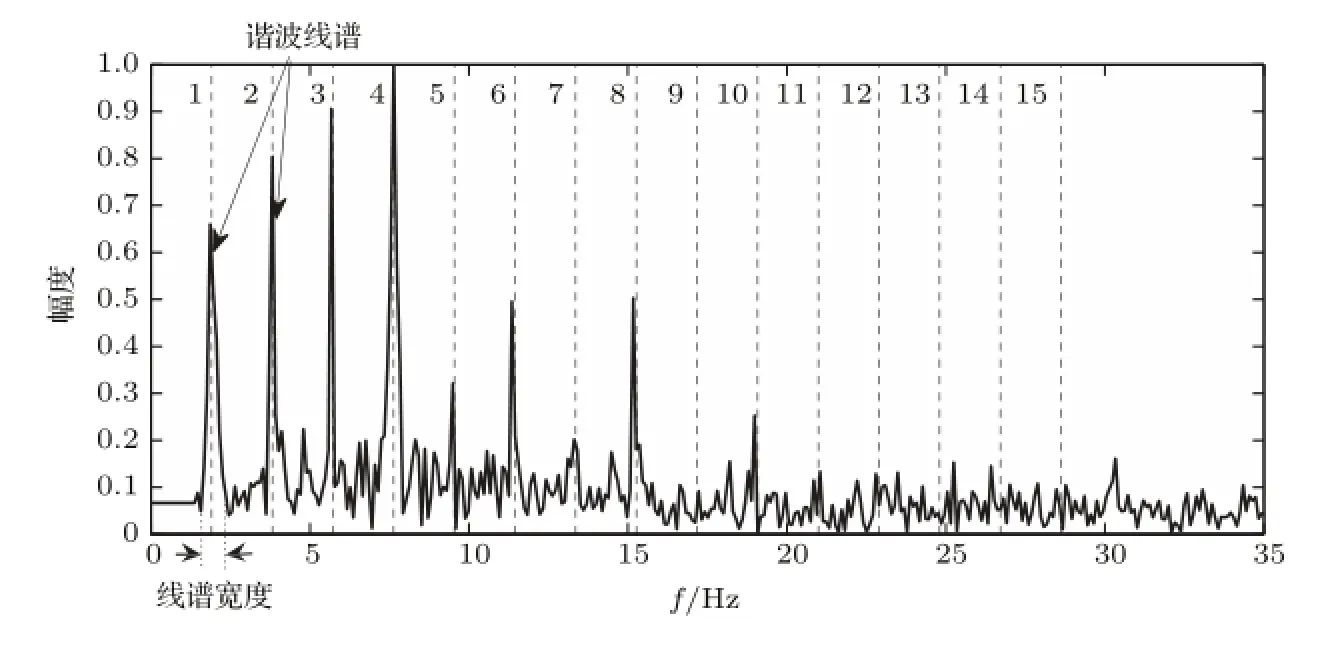
图1 某典型4叶桨目标DEMON谱图Fig.1 A typical DEMON spectrum of one 4 blades ship

图2 33维特征矢量示意图Fig.2 Schematic diagram of 33 dimension feature vector
4.3基于SVM的实验
利用混合纠错输出编码—最小汉明距离译码算法进行船舶目标螺旋桨叶片数的SVM多分类实验,并与一对多、一对一编码方式,以及最小输出编码方法进行了对比。
在实验中将样本随机分为两部分,50%用于训练,50%用于测试,应用径向基核函数SVM对样本进行实验,采用网格搜索法,在惩罚因子C=1~100之间,以1为单位步进;径向基核函数,σ=0.1~10之间,以0.01为单位步进,根据总样本的错误识别率最小原则,分别获取各SVM算法模型的最优参数,以此模型参数对训练样本、测试样本进行测试。
其中,最小输出编码方法采用了3个分类器,其具体编码为

一对余编码方法共应用了5个分类器,其具体编码为

一对一编码方法共应用了10个分类器,其具体编码为
混合纠错输出编码法的I区为前5列,对应一对余编码区,II区为后10列,对应一对一编码区,共应用了15个分类器(f1—f15)。其具体编码方式如表1所示。
按照混合纠错输出编码—最小汉明距离译码算法的过程,依据各支持向量机算法的具体编码方式,随机进行10次多分类实验。
4.4基于BP神经网络的实验
BP算法为目前应用最为广泛的神经网络学习算法,近90%的神经网络应用是基于BP算法的[11]。本文对同一批数据,采用随机抽取50%样本训练,50%进行测试,通过综合考虑和模型寻优后,采用输入层为33个神经元,中间层为12个神经元、输出层为5个神经元的三层BP神经网络进行了10次分类实验。
4.5实验结果
基于支持向量机各编码方式以及BP神经网络、近邻法的各实验结果平均正确率(百分比%)如图3所示。
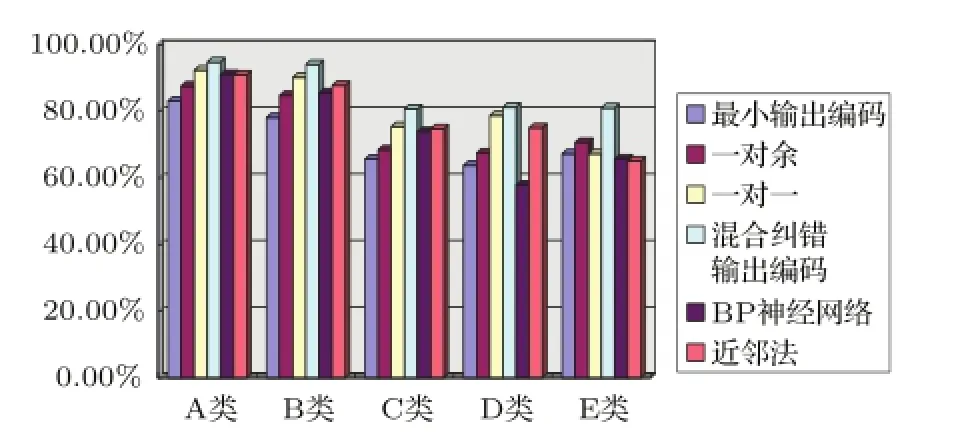
4.6实验分析
本实验属于5类目标的多分类问题,其实验结果分析如下:
(1)最小输出编码和一对余算法,采用了二符号编码方式,编码之间最小汉明距离为2,不具备纠错能力,所有的训练样本均参加每一个基础二分类的训练,分别应用了3个和5个基础两分类器进行分类,总体多类分类效果一般;
(2)一对一算法,采用了三符号编码方式,编码之间最小汉明距离为5.5,具备纠正2位输出错误的能力,每一个基础分类器仅有两类样本参加训练,其他三类样本不参加训练,虽然应用了10个基础两分类器进行分类,但由于每个基础分类器的训练样本数量少,从而总的训练计算量仍小于一对余的5个基础两分类器的总训练量,总体分类效果优于最小输出编码和一对余算法;
(3)混合纠错编码-汉明距离译码应用了二符号编码和三符号编码的混合纠错输出编码方式,编码之间最小汉明距离为7.5,具备纠正3位输出错误的能力,综合运用了一对余算法、一对一算法共15个基础两分类器进行分类,其编码配置虽然存在一定的冗余,但编码明确、训练和测试时计算量为“一对一”、“一对多”的计算量之和,不大于“一对多”算法的2倍的计算量。其总体多类分类效果最优,尤其是在C类、D类、E类不均衡小样本的分类中明显优于其他算法;
(4)经过参数寻优后的三层BP神经网络以及近邻法,其总体性能弱于一对一和混合输出纠错编码的支持向量机算法,尤其是在小样本的分类中明显弱于混合输出纠错编码算法。

表1 5分类混合纠错输出编码的具体编码方式Table 1 The detailed coding method of MECOC for 5 classes’classification
综合而言,在对船舶桨叶数分类识别中,本文所提出的混合纠错输出编码方法是一种有效的支持向量机多分类方法。
5 结论
通过对支持向量机多分类方法的理论分析和应用对比,提出了混合纠错输出编码的支持向量机多分类算法,该算法编码明确,采用了分区配置、冗余编码的方法,虽然所用的基础分类器有所增加,但总体计算量不大于2倍“一对多”算法的计算量,且具备(C2k-1)/4+1位的纠错能力。应用于船舶目标辐射噪声的螺旋桨桨叶数分类实验,表明该算法的多分类算法性能优于“一对余”、“一对一”、最小输出编码等传统的多分类方法,可适用于船舶桨叶数分类,是一种有效的多分类算法,可以进一步研究和应用。
[1]程玉胜,王易川,史广智.基于现代信号处理技术的舰船噪声信号DEMON分析[J].声学技术,2006,25(1):71-74.
CHENG Yusheng,WANG Yichuan,SHI Guangzhi.DEMON analysis of underwater target radiation noise based on modern signal processing[J].Technical Acoustics,2006,25(1):71-74.
[2]刘向东,陈兆乾.一种快速支持向量机分类算法的研究[J].计算机研究与发展,2004,41(8):1327-1330.
LIU Xiangdong,CHEN Zhaoqian.A fast classification algorithm of support vector machines[J].Journal of Computer Research and Development,2004,41(8):1327-1330.
[3]CHANG Y W,LIN C J.Feature ranking using linear SVM[J].Journal of Machine Learning Research,2008,3:53-64.
[4]Ryan Rifkin,Aldebaro Klautau.In defense of one-vsall classification[J].Machine Learning Research,2004,5:101-141.
[5]赵春晖,陈万海,赵春燕.多类支持向量机方法的研究现状与分析[J].智能系统学报,2007,2(2):11-17.
ZHAO Chunhui,CHEN Wanhai,ZHAO Chunyan.Research and analysis of methods for multiclass support vector machines[J].CAAI Transactions on Intelligent Systems,2007,2(2):11-17.
[6]黄勇,郑春颖,宋忠虎.多类支持向量机算法综述[J].计算技术与自动化,2005,24(4):61-63.
HUANG Yong,ZHENG Chunying,SONG Zhonghu. Multi-classsupportvectormachinesalgorithmsummarization[J].Computing Technology and Automation,2005,24(4):61-63.
[7]Vojtěch Franc,Václav Hlaváč.Statistical pattern recognition toolbox for Matlab user's guide[EB/OL].[2013-12-12].ftp://cmp.felk.cvut.cz/pub/cmp/articles/Franc-TR-2004-08.pdf.
[8]ALLWEIN E L,SCHAPIRE R E,SINGER Y.Reducing multiclass to binary:a unifying approach for margin classifiers[J].Journal of Machine Learning Research,2000,1:113-141.
[9]吴成东,杜崇峰,杨丽英.基于误差修正码的支持向量机大类别分类方法[J].沈阳建筑工程学院学报,2004,20(1):66-70.
WU Chengdong,DU Chongfeng,YANG Liying.A multiclass classification method of support vector machine based on error correcting output codes[J].Journal of Shenyang Arch.and Civ.Eng.Univ.,2004,20(1):66-70.
[10]HSU C W,LIN C J.A comparison of methods for multiclass support vector machines[J].Neural Networks,2002,13(2):415-425.
[11]许东,吴铮.基于MATLAB6.X的系统分析与设计——神经网络[M].西安:西安电子科技大学出版社,2003.
Ship propeller blade number classification based on multi-class support vector machine
DAI WeiguoQIU JiaxingWANG YichuanCHENG Yusheng
(Navy Submarine Academy,Qingdao 266042,China)
The paper first analyzes the common multi-class support vector machine(SVM)classification algorithms and points out the disadvantages of these algorithms,and then presents an advanced multi-class SVM classification algorithm based on mix error correcting out code(MECOC).Experiment of ship propeller blade number classification which is based on DEMON spectrum of ship target radiated noise has been done by using this algorithm.Theoretical and experimental results show that the proposed algorithm with clear code and error correction ability is an efficient multi-class SVM classification algorithm.In the ship propeller blade number classification experiment,the classification performance of this algorithm is better than one-versus-all,one-versus-one and minimum output coding(MOC)multi-class SVM classification algorithm,which is suitable for ship propeller blade number classification problem.
Ship-radiated noise,SVM,Multi-class,Propeller blade number
O427.9
A
1000-310X(2015)03-0236-07
10.11684/j.issn.1000-310X.2015.03.008
2014-09-01收稿;2015-03-17定稿
戴卫国(1968-),男,河北深州人,博士,副教授,研究方向:水声目标识别。†
E-mail:dwg1968@163.com
