基于ZnO/SiC结构的Lamb波传感器研究∗

陈　喆　范　理†　张淑仪　张　辉

（南京大学声学研究所　南京　210093）

⋄2014年度全国检测声学会议优秀论文专栏⋄

基于ZnO/SiC结构的Lamb波传感器研究∗

陈喆范理†张淑仪张辉

（南京大学声学研究所南京210093）

由于超声波传感器的工作需要极高的灵敏度和稳定度，其性能优化一直是研究的重点之一。本文采用传递矩阵法计算了基于ZnO/SiC结构的Lamb波传感器的各项性能，包括机电耦合系数，插入损耗，灵敏度以及较小的最小检测域。根据模拟结果，对Lamb波传感器的以上性能参数进行了优化，得到了优化工作条件。研究发现，Lamb波多模特性为这种传感器的性能优化提供了丰富的选择性，选择不同的模式，可以对各项性能参数进行不同目的的优化。研究结果对研制高性能的Lamb波超声传感器具有理论指导作用。

Lamb波传感器，高阶模式，碳化硅

1　引言

近年来，超声波传感器凭借着极高的灵敏度和稳定度，体积小，并且可实现无线传输等特点成为了声学研究的热点。超声波传感器的应用范围很广，包括测量温度、气压、湿度、流量、电压等物理量；借助敏感薄膜，可以用来检测有害气体微量的泄漏；在生物化学领域，可以检测溶液中微量的化学物质［1-2］。近年来，随着薄膜技术使用的不断成熟以及在微机电领域的广泛地使用，利用叉指换能器，在压电薄膜上激发出弹性声波，就可以制成各种类型的声学器件，包括Lamb波传感器［3-4］。由于薄膜材料的厚度远小于体压电材料，所以制成的传感器具有十分高的灵敏度，并逐渐替代传统的以体压电材料为载体的超声传感器［5-6］，而且薄膜基底采用硅（Si）这种材料，可以和处理外部数据的电路进行集成，因此，国际上对基于薄膜材料的超声波传感器的研究更加广泛。

近年来，人们发现碳化硅（SiC）材料具有高声速，高硬度，低成本等特点，使其在微机电系统中也具有巨大的应用潜力，因此以SiC为基底的新型超声传感器也开始得到了重视［7-9］。在超过200多种不同晶体对称性的SiC材料中，主要使用的是六角晶系（4H，6H-SiC）和立方晶系（3C-SiC），并且已经成功在这两种材料上生长了高质量的压电薄膜。其中氮化铝材料（AlN）是第一种生长在SiC基底上并用于实用化研究的材料。由于声波在AlN薄膜和SiC基底中都具有高声速的特点，因此在AlN/SiC结构中可以获得更长的声波波长，从而可以很方便地实现在超过1 GHz的高频下工作的超声波传感器［7-8］，同时另一种最常用的压电材料氧化锌（ZnO）也已经成功生长在SiC基底上［10-11］。以此为基础，基于SiC的超声波延迟线［12］以及紫外线传感器［13］也被研制成功了。

为了提高超声波传感器的性能，Caliendo等对AlN/SiC双层结构中的Rayleigh波［14］和Lamb波［15］的传播进行了大量的数值计算和理论研究，计算了声波相速度，机电耦合系数和温度系数等参数。此外，Fan等对采用SiC基底的Rayleigh波和Lamb波传感器进行了理论优化，分别采用了两种不同的压电薄膜材料ZnO和AlN，对上述所提的三个参数进行了比较［16］。除了常用的A0和S0两种基本模式，高阶模式的Lamb波也被应用在了Si基底的传感器中［17-18］。此外，最近几年，Lin等成功研制了基于AlN/SiC结构的高阶Lamb波四端口滤波器［19］，并且进一步研究了基于S3模式的Lamb波物理传感器［20］。

为了对拓展基于SiC基底的Lamb传感器在化学和生物检测方面的应用，本文采用传递矩阵法对基于敏感层/压电薄膜/SiC基底多层结构的超声波传感器中的五个重要的性能参数进行了理论模拟计算，包括机电耦合系数（kECC），质量灵敏度（Sm），电导率灵敏度（Sc），插入损耗（IL）和最小可检测质量（K）。通过选取合适的工作模式，我们可以确定工作条件使其可以同时优化上面五个重要的参数。

2　理论研究

本文使用传递矩阵法对对基于多层材料的Lamb波传感器进行理论研究，如图1所示为传感器的基本模型。图1中采用了A和B两种不同结构，其中A为WO3/ZnO/SiC三层结构，SiC为基底材料，ZnO为压电薄膜，WO3为吸附被测物质的敏感层，它们都是在超声波传感器中常用的材料；B结构是在ZnO和SiC基底之间插入一层铝（Al）薄膜作为短路电极，以加强某些频段的机电耦合系数。

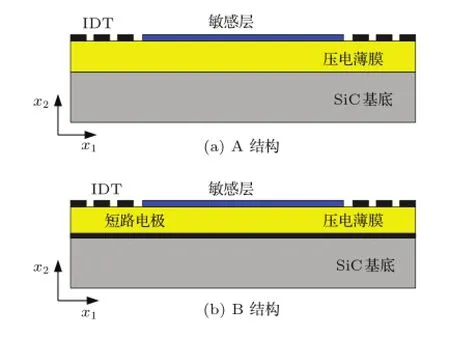
图1　超声波传感器的多层结构模型Fig.1　Models of ultrasonic sensors based on multilayered structures

多层复合材料中的声波和电磁波动方程可以表示为［21-22］

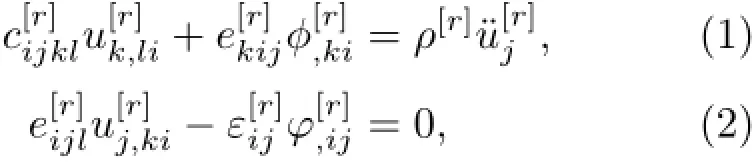
对每一层材料，由图1中的坐标系可知，Lamb波的通解可以表示为

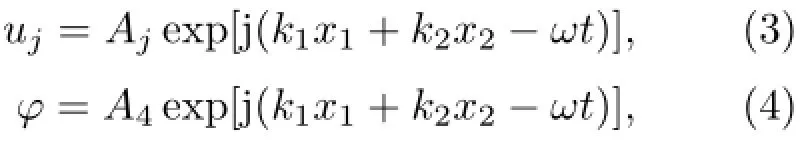
其中k1表示声波在x1方向传播的波数，k2表示声波在x2方向传播的波数，Aj，4表示位移和电势的振幅，ω表示角频率，t表示时间。将公式（3）和（4）两式分别带入公式（1）和（2）式中，可以得克里斯托夫方程：

其中Γmn为对称的4×4的克里斯托夫矩阵Γ的元素。由线性代数可知，矩阵行列式为零是方程（5）具有非零解的条件，即

因此，对于一定的角频率ω和波数k1，可以解出k2的8个根，同时可以得到相应的8个振幅解即αmq，q=1，2，···，8，因此，质点的位移和电势就可以用它们的线性叠加进行表示：

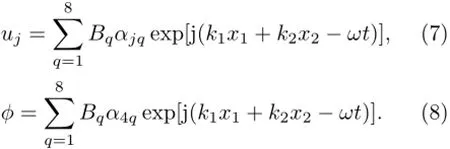
在每一层材料中，法向应力T和电位移D可以表示为

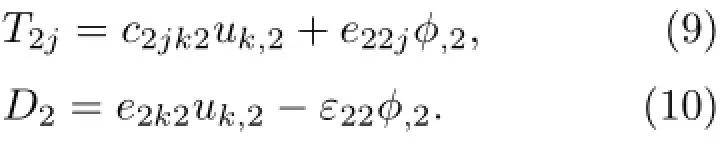
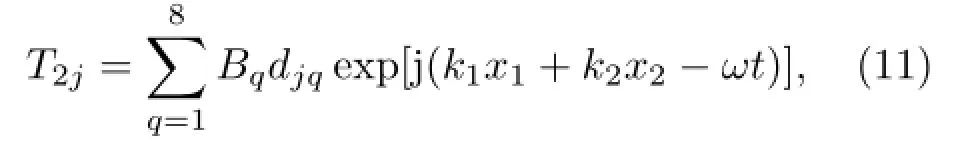
将公式（7）和（8）两式代入公式（9）和（10）可得法向应力和电位移的方程：对于多层材料，可以连续应用以上公式（22）～（27），再根据相应的边界条件，表面应力自由时则T2j=0；而当传感器上下表面开路时，电荷为零，则有σ=0；短路时，电势为零，有φ=0。将边界条件代入方程（27）中，可以得出Lamb波的色散曲线。进一步，可得机电耦合系数为

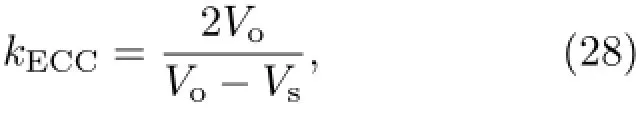
其中Vo和Vs分别为Lamb波在开路和短路时的相速度。同时，根据吸附被测质量Δm后引起的相速度变化和中心频率的偏移可以表示出相对质量灵敏度在超声波传感器的优化中，一般只关注质量灵敏度，但是研究发现，传感器的表面电导率也会随着吸附质量发生变化，同样引起相速度和中心频率的偏移因此，类比质量灵敏度可以将电导率灵敏度定义为在这种情况下，必须考虑到敏感层中的传导电流的影响，并且对电磁波动方程和电学边界条件进行修正。其实质只需要在等效介电常数εik中引入电损耗量得到εik-σik/jω。此时，相速度变为复数V0-jV1（V0，V1＞0），其中虚数部分表示传导电流引起的电损耗。进一步可以得到，由电损耗引起的插入损耗和相应的最小检测质量系数则可以分别表示成［22］：

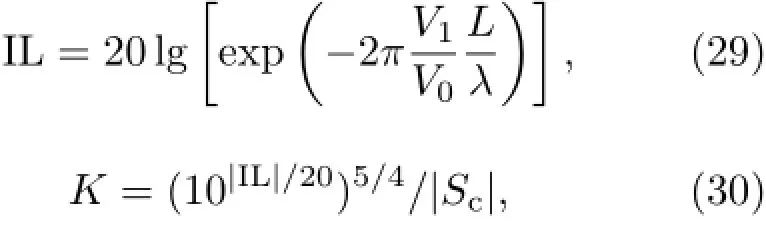
其中λ是传感器工作时的波长，而L是激发换能器和接收换能器之间的距离。

本文主要根据以上理论对Lamb波反对称模式A0-A1以及对称模式S0-S1四种模式进行模拟，计算这些模式下Lamb波传感器的机电耦合系数，插入损耗，质量灵敏度，电导率灵敏度，并在此基础上获得了传感器的最小可检测质量。其中模拟中使用的主要材料参数如表1所示。在模拟中，假设WO3的密度和电导率随吸附质量变化分别为20 ng/cm2 和10 mS/m3。

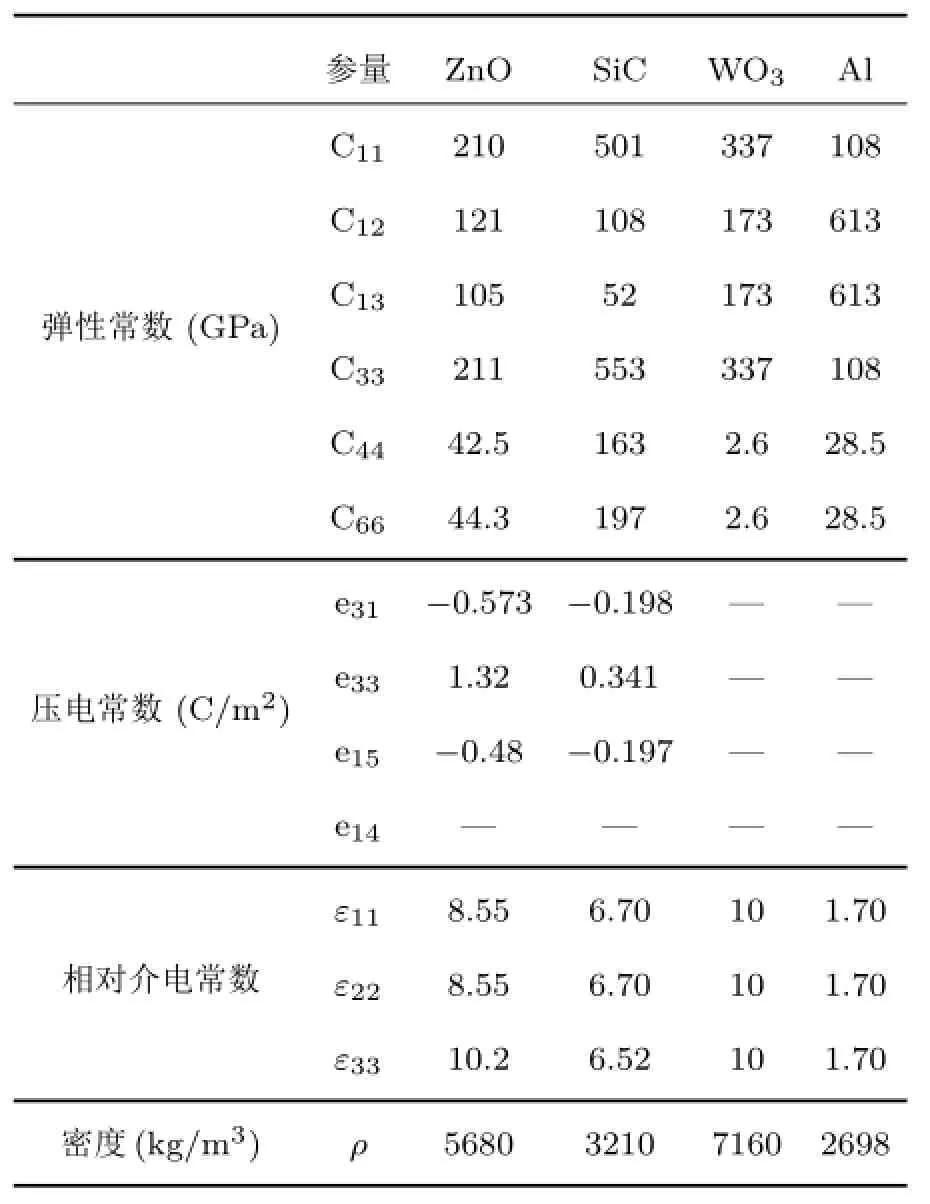
表1　ZnO薄膜和SiC基底的弹性常数，压电常数，相对介电常数和密度Table 1 Elastic constants，piezoelectric constants，relative dielectric constants and densities of ZnO piezoelectric film and SiC substrate

3　结果与讨论

对Lamb波传感器的优化，首先要保证有较高的机电耦合系数，增强激发声波的强度，并增加传感器的信噪比。此外，传感器的灵敏度是十分重要的参数，这主要由质量灵敏度和电导率灵敏度共同决定。同时，需要注意的是，较高的电导率灵敏度往往伴随较高的电损耗，同样会使插入损耗和最小可检测质量增加。因此，对Lamb波传感器优化的目标是获得较大的机电耦合系数，质量灵敏度和电导率灵敏度，以及尽可能减小损耗和最小可检测质量。

3.1色散曲线

图2所示为A结构的4种不同相对基底厚度，以SiC为基底的Lamb波传感器A0～S1种模式的色散曲线，其中hs为SiC基底的厚度，横轴表示为压电薄膜的相对厚度hf/λ，hf为压电薄膜ZnO的厚度，λ 为Lamb波的波长，纵轴为相速度v。由于短路电极厚度远小于其它几层材料，所以它对相速度的影响很小，因此，图2中只列出A结构的相速度。

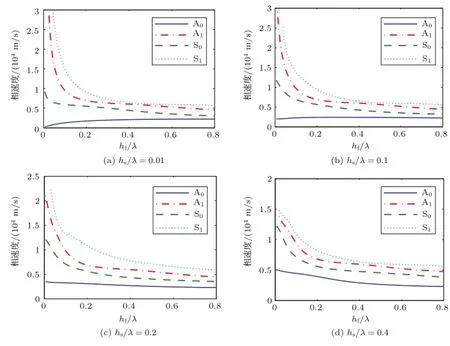
图2　以SiC为基底的Lamb传感器四种不同相对基底厚度的四种模式色散曲线Fig.2 Dispersion curves Lamb wave sensors based on SiC substrates with different relative thicknesses

3.2机电耦合系数和质量灵敏度

图3所示为四种不同的相对SiC基底厚度的Lamb波传感器的机电耦合系数和质量灵敏度，图3中表示了A和B两种结构的机电耦合系数，而质量灵敏度只选择了A结构，因为质量灵敏度几乎不受叉指结构的影响。从图3中可以看出，A0和S0两个模式的机电耦合系总体要高于A1和S1模式，尤其是B结构的S0模式可以达到6%。但是，A1和S1模式的质量灵敏度要明显高于A0和S0两个模式。因此，我们基于这两个参数对传感器性能进行第一步优化，将kECC≥1%和|Sm|≥2.5×10-5的工作条件总结列在表2中。从表2中可以看出，采用A1模式可以同时获得较高的质量灵敏度和机电耦合系数。使用A结构，当相对基底厚度hs/λ=0.01时，在相对薄膜厚度hf/λ=0.03处，机电耦合系数可以取到4.4%，同时质量灵敏度也达到了5.3×10-5。同样是A1模式，当相对基底厚度hs/λ=0.2时，在相对薄膜厚度hf/λ=0.15，可以获得5.0×10-5的质量灵敏度，此时的机电耦合系数为1.4%。在B结构中，A1模式当hs/λ=0.1和hf/λ=0.19时，可以获得5.6×10-5的质量灵敏度，此时的机电耦合系数为1.5%；而当相对基底厚度hs/λ分别为0.2和0.4时，在相对薄膜厚度为hf/λ=0.15～0.17，质量灵敏度可以分别取得5.4×10-5和4.6×10-5，同时可以获得机电耦合系数分别为2.1%和1.2%。B结构中S1模式在相对基底厚度hs/λ为0.1和0.2时，在相对薄膜厚度hf/λ分别为0.036和0.042处，质量灵敏度可以达到2.5×10-5，机电耦合系数也可以分别达到2%和1%，可以满足优化工作条件。

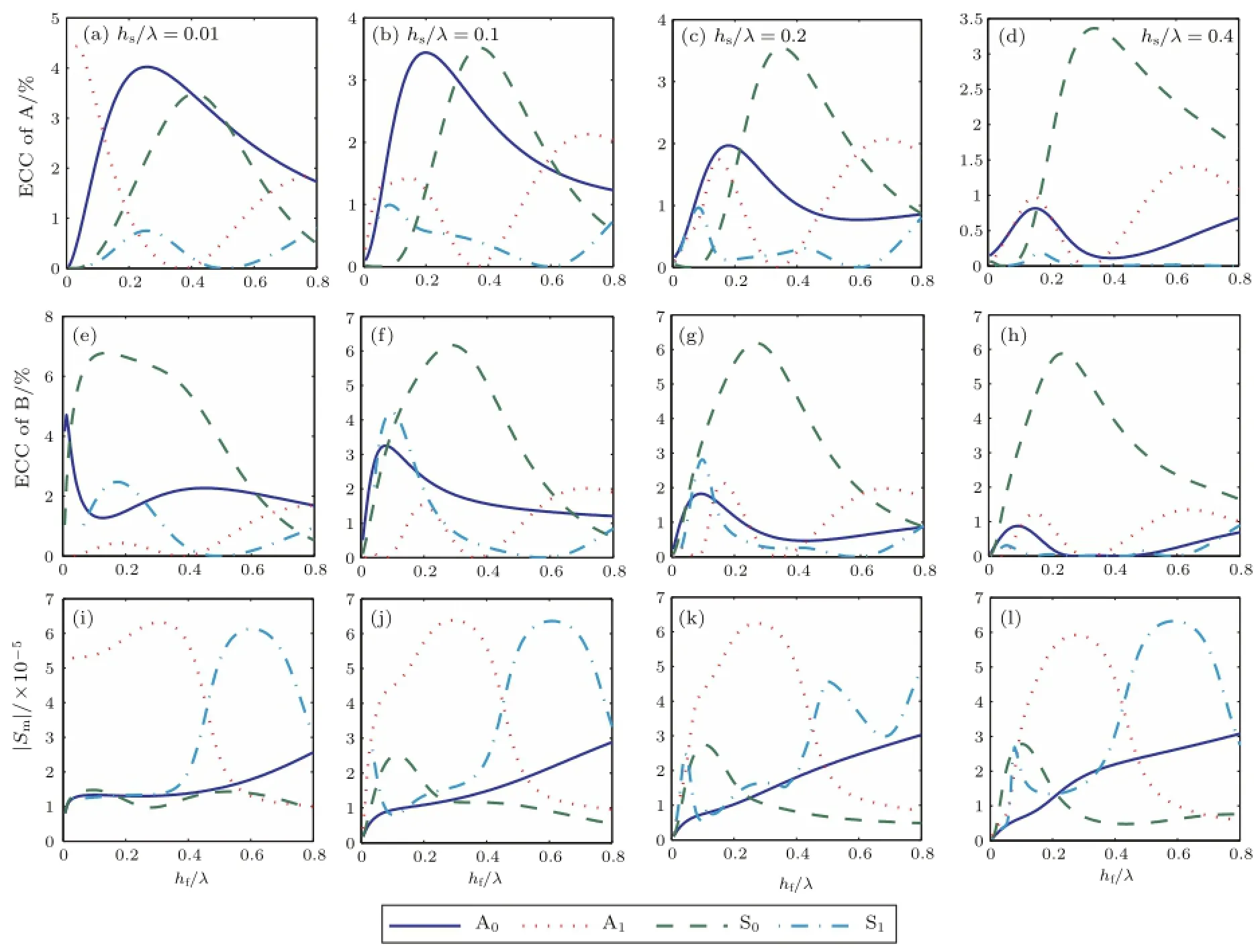
图3　以SiC为基底的Lamb传感器四种不同相对基底厚度的机电耦合系数和质量灵敏：（a）～（d）为A结构的机电耦合系数；（e）～（h）为B结构的机电耦合系数；（i）～（l）为质量灵敏度Fig.3 ECCs and Smof Lamb wave sensors based on SiC substrates with different relative thicknesses：（a）～（d）ECCs with IDT structures A；（e）～（h）ECCs with IDT structures B；（i）～（l）mass sensitivities

3.3电导率灵敏度，插入损耗和最小可检测质量

当传感器表面吸附被测物质时，除了产生质量负载，其敏感层的电导率也会发生变化，从而引起中心频率的偏移，图4、图5分别以SiC为基底的A结构和B结构的Lamb传感器的电导率灵敏度，插入损耗和最小可检测质量。类似于机电耦合系数，由图4和图5可以见，A0和S0模式的电导率灵敏度要高于A1和S1模式，如在A结构中A0模式的电导率灵敏度可以达到4×10-5。但是，较高的电导率灵敏度意味着更强的电学扰动，同时也伴随着较高的电损耗，比如S0模式由电扰动引起的插入损耗可以达到600 dB，从而降低了传感器信噪比，使最小可检测质量增大，这是需要避免的。因此，根据表2，从满足机电耦合系数可和质量灵敏度优化条件的点中，再次筛选出合适的工作条件，使其具有较大的电导率灵敏度，较小的插入损耗和最小可检测质量。在优化工作条件e和g中，S1模式的插入损耗都比较小，不超过2 dB，但是其电导率灵敏度比较小，只有10-8量级；而工作条件d，f和h中，A1模式具有较高的电导率灵敏度，但是插入损耗超过70 dB，最小可检测质量系数为K≈10-10。此外，工作条件b 和c，A1模式都可以取到相对较高的电导率灵敏度|Sc|＞4×10-6，并且插入损耗都不超过46 dB。其中，最优化的工作条件是a，其电导率灵敏度可以达到|Sc|=1.3×10-5，同时插入损耗IL=16 dB和最小可检测质量K≈10-6，都是相对比较小的，可以满足同时优化五个条件。

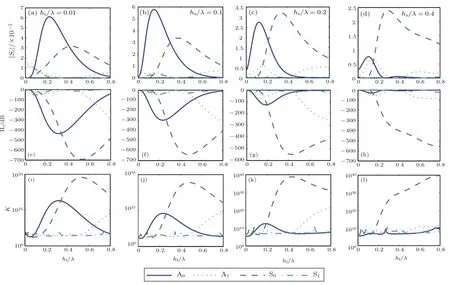
图4　以SiC为基底的A结构的Lamb传感器的电导率灵敏度（a）～（d），插入损耗（e）～（h）和最小可检测质量（i）～（l）Fig.4 Performances of Lamb wave sensors based on SiC substrates with IDT structure A：（a）～（d）Sc；（e）～（h）IL and（i）～（l）K

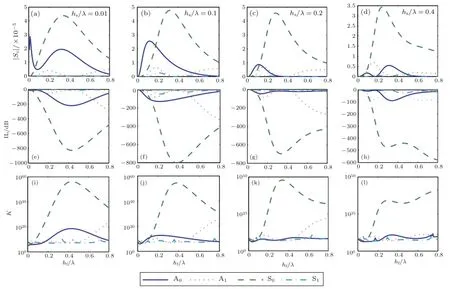
图5　以SiC为基底的B结构的Lamb传感器的电导率灵敏度（a）～（d），插入损耗（e）～（h）和最小可检测质量（i）～（l）Fig.5 Performances of Lamb wave sensors based on SiC substrates with IDT structure B：（a）～（d）Sc；（e）～（h）IL and（i）～（l）K

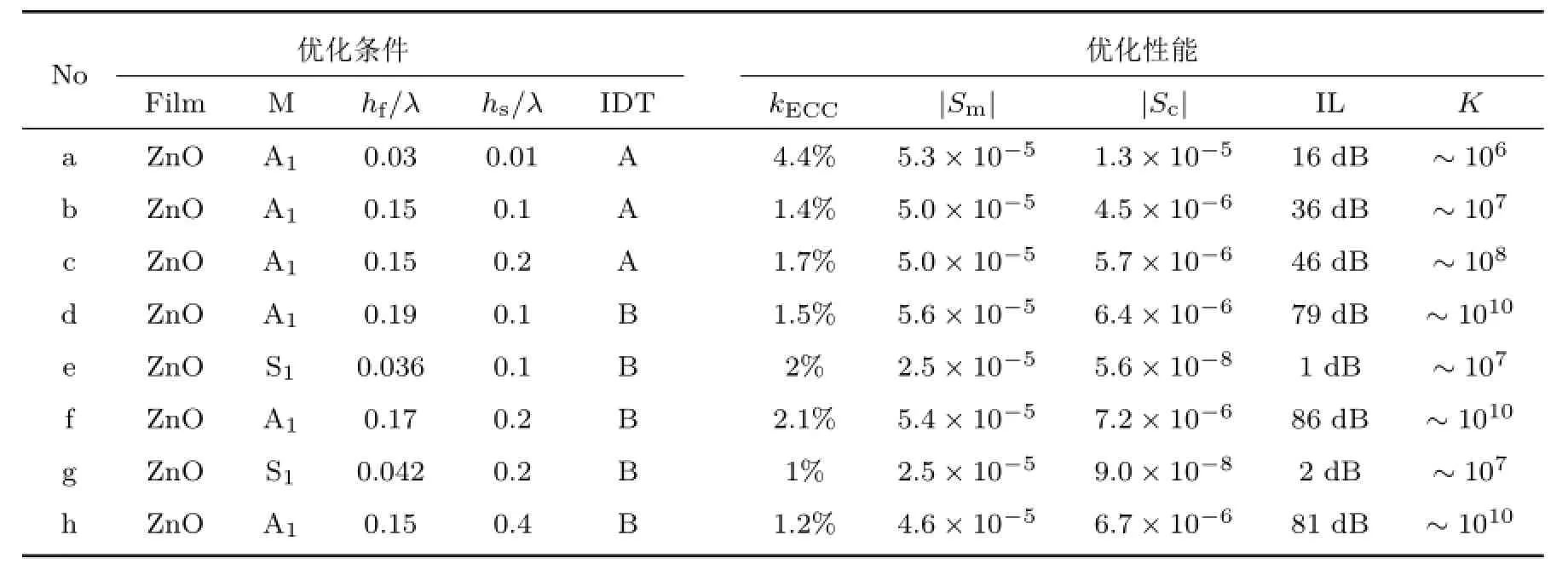
表2　不同模式下的优化工作条件Table 2 Optimized working conditions and performances Lamb wave sensors adopting different modes of Lamb waves

4　结论

本文使用传递矩阵法对对基于WO3/ZnO/SiC三层材料的Lamb波传感器进行了理论研究，分别计算了A和B两种不同结构的Lamb波传感器的性能，主要对A0-A1以及S0-S1四种Lamb波模式进行了性能模拟，计算了这些模式下Lamb波传感器的机电耦合系数，插入损耗，质量灵敏度，电导率灵敏度，并在此基础上获得了传感器的最小可检测质量。为了获得最优的Lamb波传感器性能，必须同时获得高机电耦合系数，低插入损耗，高灵敏度并且实现更小的可检测质量。根据计算结果，我们选择了合适的工作条件，实现了同时对以上五个参数进行优化的目标，为基于SiC的超声波传感器的实用化研究打下了基础。

［1］TALBI A，SARRY F，BRIZOUAL L L，et al.Sezawa mode SAW pressure sensors based on ZnO/Si structure［J］. IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2004，51（11）：1421-1426.

［2］CALIENDO C，VERARDI P，VERONA E，et al.Advances in SAW-based gas sensor［J］.Smart Materials and Structures，1997，6（6）：689-699.

［3］ZHOU F M，LI Z，FAN L，et al.Experimental study of Love-wave immunosensors based on ZnO/LiTaO3structures［J］.Ultrasonics，2010，50（3）：411-415.

［4］WHITE R M，WICHER P J，WENZEL S W，et al. Plate-mode ultrasonic oscillator sensors［J］.IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，1987，34（2）：162-171.

［5］VELLEKOOP M J.Acoustic wave sensors and their technology［J］.Ultrasonics，1998，36（1-5）：7-14.

［6］D'AMICO A.SAW sensors［J］.Sensors and Actuators，1989，17（1-2）：55-66.

［7］TAKAGAKIY，SANTOSPV，WIEBICKEE，et al.Superhigh-frequency surface-acoustic-wave transducers using AlN layers grown on SiC substrates［J］.Applied Physics Letters，2002，81（14）：2538-2540.

［8］UEHARA K，YANG C M，FURUSHO T，et al.AlN epitaxial film on 6H-SiC（0001）using MOCVD for GHz-band SAW devices［C］.Proceeding of International Ultrasonics Symposium，2003.

［9］LIN C M，LIEN W C，FELMETSGE V V，et al.AlN thin films grown on epitaxial 3C-SiC（100）for piezoelectric resonant devices［J］.Applied Physics Letters，2010，97（14）：141907.

［10］CHEN Y，SARAF G，REYES P I，et al.Structural，electrical，and piezoelectric properties of ZnO films on SiC-6H substrates［J］.J.Vac.Sci.Technol.B，2009，27（3）：1631.

［11］HICKERNELL F S.The characterization of zinc oxide films on silicon carbide［C］.Proceeding of International Ultrasonics Symposium，1998.

［12］PHAN D T，SUH H C，CHUNG G S.Surface acoustic wave characteristics of ZnO films grown on a polycrystalline 3C-SiC buffer layer［J］.Microelectronic Engineering，2011，88（1）：105-108.

［13］PHAN D T，CHUNG G S.Fabrication and characteristics of a surface acoustic wave UV sensor based on ZnO thin films grown on a polycrystalline 3C-SiC buffer layer［J］. Current Applied Physcis，2012，12（2）：521-524.

［14］CALIENDO C.Theoretical investigation of high velocity，temperature compensated Rayleigh waves along AlN/SiC substrates for high sensitivity mass sensors［J］.Applied Physic.Letters，2012，100（2）：021905.

［15］LIN C M，CHEN Y Y，PISANO A P.Theoretical investigation of Lamb wave characteristics in AlN/3C-SiC composite membranes［J］.Applied Physcs Letters，2010，97（19）：193506-193506-3.

［16］FAN L，ZHANG S Y，GE H，et al.Theoretical investigation of surface acoustic wave devices based on different piezoelectric films deposited on silicon carbide［J］.Journal of Applied Physics，2013，114（2）：024504.

［17］PALMA A.Acoustic Lamb wave-electric field nonlinear interaction in YZ LiNbO3plate［J］.Applied Physics Letters，1985，46（1）：25-27.

［18］PALMA A.Lamb-wave electroacoustic voltage sensor［J］. Journal of Applied Physics，1985，58（8）：3265-3267.

［19］LIN C M，CHEN Y Y，FELMETSGE V V，et al.Twoport filters and resonators on AlN/3C-SiC plates utilizing high-order Lamb wave modes［C］.Micro Electro Mechanical Systems（MEMS），2013 IEEE 26th International Conference on.IEEE，2013.

［20］LIN C M，CHEN Y Y，FELMETSGE V V，et al.Acoustic characteristics of the third-order quasi-symmetric Lamb wave mode in an AlN/3C-SiC plate［C］.IEEE International Ultrasonics Symposium，Prague，Czech Republic，2013.

［21］FAN L，ZHOU F M，WANG C，et al.Influence of surface conductivity on sensitivity of acoustic wave gas sensors based on multilayered structures［J］.IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2011，58（2）：451-460.

［22］FAN L，GE H，ZHANG S Y，et al.Optimization of sensitivity induced by surface conductivity and sorbed mass in surface acoustic wave gas sensors［J］.Sensors and Actuators B，2012，161（1）：114-123.

Research on Lamb wave sensor based on ZnO/SiC structure

CHEN ZheFAN LiZHANG ShuyiZHANG Hui
（Lab of Modern Acoustics，Institute of Acoustics，Nanjing University，Nanjing 210093，China）

The optimization of the ultrasonic sensor is the key to the research because high sensitivity and stability must be assured.In this paper，the transfer matrix method is used to calculate the performance of the Lamb wave sensor based on ZnO/SiC structure，in which the electromechanical coupling coefficients，sensitivities，insert losses and minimum detectable masses are simulated.According to the simulated results，proper working conditions are obtained for optimizing the abovementioned parameters.It is found that different modes of the Lamb wave can be used to optimize different performance parameters.The research results are useful to the design of high-performance Lamb wave sensors.

Lamb wave sensor，High-order mode，SiC

TP212.1

A

1000-310X（2015）03-0207-09

10.11684/j.issn.1000-310X.2015.03.004

2014-12-16收稿；2015-03-17定稿

∗973项目课题（2012CB921504），国家自然科学基金项目（11374154，10904067，11174142）

陈喆（1991-），男，江苏南通人，硕士研究生，研究方向：光声学。

E-mail：Fanli@nju.edu.cn