基于有限元的空耦超声相控阵Lamb波激发与检测∗

张 迪†吴先梅

（中国科学院声学研究所声场声信息国家重点实验室　北京　100190）

⋄2014年度全国检测声学会议优秀论文专栏⋄

基于有限元的空耦超声相控阵Lamb波激发与检测∗

张 迪†吴先梅

（中国科学院声学研究所声场声信息国家重点实验室北京100190）

近些年来，基于非接触式空气耦合超声换能器的无损检测技术在常规板材、纤维复合材料、层状结构材料、粘接界面等的检测中已经有了长足的发展。但是由于空气耦合超声自身特性的限制，如何提高空气声换能器的发射效率和接收灵敏度、提高接收信号的信噪比已成为这一领域的重要课题。本文提出了电容式空气超声换能器阵列的构建和制作方法，能够有效提高空气耦合超声换能器的发射效率和接收灵敏度，并应用有限元方法对一维空气声线阵的声束动态偏转特性进行了模拟，构建流固耦合模型对空气声场及各向同性板材中的位移场进行了计算。计算发现，相控阵声束动态偏转在板中能够激励出Lamb波A0和S0模式，并对其频域特性进行了分析。此模型可以用于模拟空气耦合超声相控阵对板材的Lamb波无损检测。

空气耦合超声换能器，无损检测，Lamb波激发，一维线性相控阵，有限元仿真

1　引言

近年来，超声已经在工业无损检测中获得了很多的应用，其中的非接触式超声激发及检测方法由于可以避免在换能器与待检材料之间使用耦合剂（通常为油、凡士林或蜂蜜等）作为媒介，并且可以实现快速在线检测等优点，将有望在工业检测中得到越来越广泛的应用。通常的非接触式超声激发及接收方法主要包括使用空气耦合超声换能器［1］（ACUT）、激光超声方法［2］（LU）、或电磁声换能器［3］（EMAT）等。通过激光激发材料中的超声并且使用换能器或干涉仪进行检测的方法具有频带宽、适应性好等优点，但是由于成本较高不适合在线检测等问题，现在还主要限于实验室研究阶段。电磁超声换能器由于只适用于金属等磁导材料，也限制了其进一步的应用。作为一种低成本普适性好的超声检测解决方案，空气耦合超声换能器能够用于金属、聚合物或复合材料的检测，并且常规的空气声换能器已经在常规板材、纤维复合材料［4］、层状结构材料、粘接界面［5］等的检测中有了不少应用。

应用空气耦合超声换能器这种非接触式检测方法的困难主要在于空气与固体材料的声阻抗失配，在流固界面传播时超声波会发生很大的衰减。这种情况发生在换能器与空气界面和空气与待检材料界面，例如在空气-铝材料界面垂直入射的200 kHz单频超声会发生54 dB的衰减。另外超声在空气中传播时也有较大的衰减，在高频情况下衰减尤其严重。在常用超声频段（100 kHz～1 MHz），空气中传播的超声衰减系数与频率的关系为αdB=1.64f2×10-10（dB/m）［6］，例如对于1 MHz的超声波在传播30 cm后衰减了49 dB，因此要实现对材料在较低频段下的空气耦合超声检测，换能器需要很高的发射效率及接收灵敏度，这样才能得到较高的信噪比，从而可以实现对固体材料的缺陷或损伤进行无损检测或成像。本文基于电容式的空气耦合超声换能器技术提出了用于无损检测的空气耦合阵列，通过有限元模型模拟了相控阵动态偏转时空气中的声场，以某一种入射角度斜入射到板中从而激发出板中对应的Lamb波模式，进而实现对板的材料和结构检测。

2　电容式超声换能器阵列

目前，主要有两种类型的空气耦合超声换能器，即压电式空气超声换能器和电容式空气超声换能器。应用压电式空气超声换能器时，由于压电材料与空气的声阻抗相差较大，存在声阻抗失配问题，通常会通过在换能器辐射面增加一层或数层阻抗匹配层以提高超声波发射效率和接收灵敏度。由于压电式换能器的特点和匹配层的滤波作用，限制了压电空气耦合超声换能器的频带宽度。

另一种解决方案是使用电容式的空气超声换能器，它的结构如图1所示，它是根据金属基底和导电薄膜之间的电容相互作用的原理发射超声波［7］。金属基底表面通过加工产生一定的粗糙度，与聚合物金属镀膜间形成平行电容器，通过在上表面金属镀层与金属基底间加一定的偏置电压Vbias，由于静电作用上表面膜会压紧基底表面。在上下表面间施加相应频率的电压信号Vsignal，上表层镀层与基底表面间的粗糙空穴成为声学共振腔，从而通过上表面薄膜向空气中发射与输入电压信号成正比的声波振动。

图1　电容式空气耦合超声换能器阵列结构及其相控阵聚焦示意图Fig.1 Schematic of the air-coupled capacitive ultrasonic linear array and its focusing

当此换能器用作接收器时，到达表面的空气中的声波振动压迫换能器表面，使得上表面与基底间的电容发生变化，从而使输出电压与到达的声波振动成正比变动。由于使用金属镀层的聚合物薄膜作为与空气接触的材料，并且相互作用发生在薄膜面下，解决了传统压电材料的阻抗失配问题，能够达到较高的发射效率和接收灵敏度。由于基底表面的空穴共振特性，电容式空气超声换能器也具有较宽的频带宽度。如图1所示，通过将换能器基底进行切割并在其间填注环氧树脂作为填充剂，周期排列的基底金属柱作为一维线阵阵元。构建的一维线阵通过激发信号的延时发射，成为一维空气声相控阵。为了抑制在空气中形成的旁瓣，相控阵阵元空间周期应小于λmin/2［8］，其中λmin为发射或接收的声波波长的最小值。由于在空气中传播的超声波长很小，频率为200 kHz的声波波长约为1.7 mm，16阵元的一维线阵总长度为13.6 mm。通过采用不同的阵元信号延时法则，该相控阵可以实现声波聚焦或偏转等特性。

3　基于有限元的流固耦合数值模型

根据电容式空气声一维相控阵构建流固耦合的有限元模型，用于模拟空气中相控阵换能器的激发和接收以及空气声耦合在各向同性板中的波的激发及特性。有限元模型示意图如图2所示。

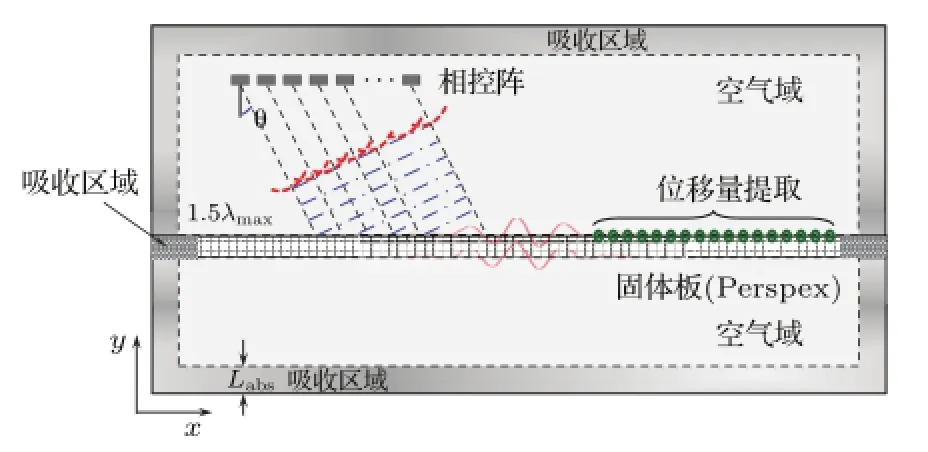
图2　利用空气耦合超声线阵换能器激发板中的Lamb波及其检测的有限元模型示意图Fig.2 Finite element model of Lamb wave excitation with linear array in air-solid-air domain condition

模型中包含空气-固体-空气域，固体材料参数采用聚合物Perspex材料，空气与固体域的外围边界需要使用吸收层边界条件吸收入射声波。激励声源为空气中的一维相控阵，并通过在频域内各阵元间的相移实现声束偏转或聚焦。通过控制相控阵阵元之间的相移可以产生波前为平面波的声场。通过改变各阵元的相位延迟量就可以改变声束的入射角度，即可在板中激发出不同模式的Lamb波。

3.1有限元模型的PDE形式

二维有限元模型设定包括空气-固体板材-空气计算域，采用Comsol中的PDE模块［9］进行求解。在考虑与时间无关的频域下的波在介质中传播的PDE方程，如式（1）所示：

其中u为变量，在空气域中为声压p，在固体中为位移矢量u，f为声源。后面两个方程分别为诺依曼边界条件和狄利克莱边界条件，各个边界的边界条件根据这两种条件分别设定。空气域与固体中的各参数分别不同，在空气域中，各参数为

其中Kf为空气的体模量，ρf为空气的密度，ω为入射波的圆频率。F为换能器或阵列在相应区域施加的源。在固体中，式（1）中的各参数分别为

对于具有正交特性的固体材料来说，由于晶体的对称性，材料弹性常数Cij的非零分量只有C11，C22，C12，C66，对于各向同性材料，可以用C11和C66分量来表示，有关系C22=C11，C12=C11-2C66，因此式（3）参数c各分量为

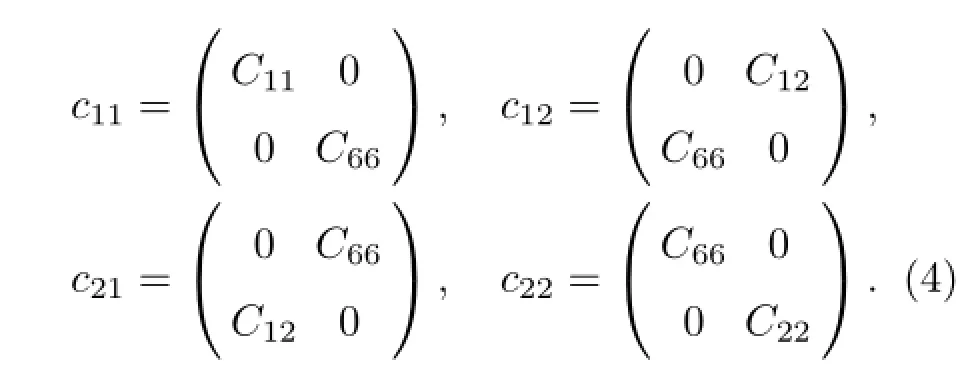
3.2吸收层及边界条件

有限元模型使用频域波动方程静态求解器进行求解，对于边界反射回波并不能如同在时域中使用时间窗口进行限制，因此在求解域的周围要设置吸收边界消除反射回波，用于模拟无限传播媒质的情况。这里采用频域媒质粘滞吸收层［10］，同时应用PML完美匹配吸收层的概念。对频域的材料参数来说，使用材料的复数弹性常数表示材料的可压缩性能。复数的实部是可压缩常数，其虚部表示声波在其中的粘滞阻尼。因此，通过逐渐增加吸收层内的粘滞来达到逐步吸收声波的目的，并且通过将吸收层的媒质阻抗设定为和波传播媒质内的相同，从而避免界面上入射波的反射。对空气来说，声阻抗为，因此需要在声传播区域内及吸收层之间保持材料的声阻抗Z不变。根据这些设定要求，将吸收层内的材料的体模量及密度分别设定为

其中为吸收层区域内的空气的体模量，对于固体材料来说对应刚度常数模量为声波传播区域内的空气的体模量分别为吸收层和传播区域内的空气密度。d为吸收层内的某一点到吸收层与波传播区域的距离，La为吸收层的厚度。常数A决定了吸收层对入射波吸收的强度。通过适当的常数A的设定，使得反射回波的强度衰减达到相应的要求，通常要求反射回波的幅度小于入射波的0.1%。通过数值实验发现，这样设定的有限元的吸收层厚度达到La=1.5λ时可以得到符合要求的吸收效果。在固体材料中使用和空气中的吸收层相似的设定，吸收层处于固体材料的两端，其厚度为1.5倍的纵波波长［11］。

对于二维流固耦合的有限元模型，需要在空气与固体材料边界设置流固耦合边界条件，即式（1）中的诺依曼边界条件。对于弹性接触界面来说，需要符合在边界处应力连续及法向位移连续的条件。因此可以分别在空气中通过设置位移连续，利用式（1）中的诺依曼边界条件设置为

其中n为边界法向矢量，规定正方向为从固体指向流体，ρf为流体的密度，us为固体的边界处法向

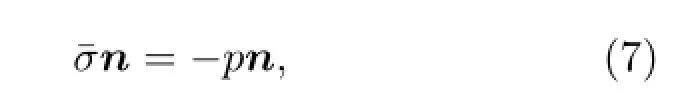
其中¯σ为固体在界面处的应力张量，p为流体中的声波声压。

3.3空气超声相控阵发射及接收模型

空气耦合超声激励的重要问题是流固界面的反射及空气中的超声衰减，因此需要较高的发射效率及接收灵敏度。对于使用相控阵发射及接收的空气声阵列来说，需要在有限元模型中相应的声源对各个阵元进行相位延迟或提前，选择一维相控阵的声束动态偏转模式，以形成具有某一特定入射角的波束从而可以激励出所需的Lamb波模式。由于有限元模型直接在频域求解，因此可以对相控阵的各个阵元所形成的声压在频率域直接进行相位变换。

对于发射换能器的各阵元来说，各阵元发射的声场叠加形成的总声场的声压为

其中pi（x，y；ω）为各个阵元在二维坐标下的频域的发射声场声压，Δφi为施加于各阵元对应的相移，Δli为各阵元中心相对于第一阵元起点沿声场波束指向方向的距离。

而对于接收换能器来说，需要在各阵元接收到相应信号后进行相应相位变换，然后对所有经过处理的波形进行叠加后得到某一偏转方向的接收声场的灵敏度表示。接收相控阵接收到的总的声场声压为

其中PR（x，y；ω）为接收换能器接收到的场点的声场声压，Δdi为各接收相控阵阵元中心相对于某一阵元起点沿接收指定方向的投影距离。对于发射换能器来说，各阵元间发射声场的相移为提前Δφi，而对于接收换能器需要对各个阵元的相位进行延迟达到声束沿某一方向偏转接收的目的。位移矢量。在固体中，利用法向应力连续设置边界条件为

4　基于有限元的空气声激发Lamb波模型结果

使用空气耦合相控阵进行导波激发及检测需要选择板中的Lamb波的某一模式，对于低频空气超声来说，一般使用低阶的A0模式或S0模式。由斯涅耳定律，利用一维线性相控阵的波束偏转模式。

对于以某一中心频率入射的波形来说，其入射角度满足条件sinθi=ca/cl，其中ca为空气中的声速，cl为沿板传播的某一模态指定频率Lamb波的相速度［12］。

有限元模型使用4 mm厚度Perspex材料板，从空气中入射的超声使用中心频率为250 kHz的高斯包络的Toneburst信号进行激发。如图3（a）所示，为空气声以16.5°入射（Lamb波A0模式的入射角）在频率为250 kHz时的空气声压及固体中的法向应力。可以看出，使用这个角度入射的空气声可以在板中激发出明显的沿板传播的反对称模态。由于是在频域求解，通过求解各个频率下激发的Lamb波情况，并分别提取出各个频率下板表面的法向位移量，从而可以得到对应Lamb波的波数频率（k-f）域的频散图，如图3（b）所示，可以看出，板中激发出了比较纯的A0模式。

图3（c）为激发出的Lamb波的S0模式，声束入射角度为9.9°，从固体中的法向位移显示可以看出，空气超声激发出的是沿板传播的对称模式。通过变换到频散图3（d）可以看出，在原有A0模式下，出现了S0模式，同时A0模式强度减弱，但并未消失，即在此入射角度上空气声激发出的S0模式仍叠加有一定强度的A0模式。通过使用空气声激发的某一模式对检测对象的变化情况，即可以实现空气耦合超声相控阵Lamb波的在线无损检测。

图3　利用空气耦合超声相控阵偏转扫描激发板中的Lamb波模式示意图及对应的频率波数频散图Fig.3 The excited Lamb wave modes in plate through the incident of beam steering plane wave emitted by air-coupled ultrasonic linear array and their corresponding k-f domain spectrums

5　结论

本文引入了一种新的电容式空气声换能器，并基于此构建了一维线性相控阵。通过基于PDE的有限元模块对相控阵声束动态偏转激发流固耦合模型进行了数值模拟，有限元模型需要设置空气域与固体域的偏微分方程形式、粘滞匹配吸收层、耦合边界条件及相控阵阵元相移等。有限元模型激发出二维各向同性板中的板波，通过控制偏转入射角度，分别激发出了板中的Lamb波的A0模式或S0模式。此模型可以用于模拟空气耦合超声相控阵对板材的Lamb波无损检测中。

［1］HIETANEN J，STOR-PELLINEN J，LUUKKALA M.A model for an electrostatic ultrasonic transducer with a grooved backplate［J］.Meas.Sci.Technol.，1992，3（11）：1095-1097.

［2］MONCHALIN J P.Laser-ultrasonics：from the laboratory to industry［P］.Thompson DO.AIP Conf.Proc.，2004，700（1）：3-31.

［3］GAO H，ALI SM，LOPEZ B.Inspection of austenitic weld with EMATs［P］.Thompson DO，AIP Conf.Proc.，2010，1211（1）：1175-1181.

［4］KAYS R，DEMENKO A，MAEIKA L，et al.Air-coupled ultrasonic non-destructive testing of aerospace components［J］.Insight-NDT and Cond.Moni.，2007，49（4）：195-199.

［5］SCHINDEL W，FORSYTH S，HUTCHINS A，et al.Aircoupled ultrasonic NDE of bonded aluminum lap joints［J］. Ultrasonics，1997，35（1）：1-6.

［6］BASS E，SUTHERLAND L C，ZUCKERWAR A J，et al.Atmospheric absorption of sound：Further developments［J］.J.Acoust.Soc.Am.，1995，97（1）：680-683.

［7］MATTILA P，TSUZUKI F，VAATAJA H，et al.Electroacoustic model for electrostatic ultrasonic transducers with V-grooved backplates［J］.IEEE Trans.Ultrason.Ferroelectr.Freq.Control，1995，42（1）：1-7.

［8］LELEUX A，MICHEAU P，CASTAINGS M.Long range detection of defects in composite plates using lamb waves generated and detected by ultrasonic phased array probes［J］.J Nondestruct Eval.，2013，32（2）：200-214.

［9］HOSTEN B，CASTAINGS M.Finite elements methods for modeling the guided waves propagation in structures with weak interfaces［J］.J.Acoust.Soc.Am.，2005，117（3）：1108-1113.

［10］GALÁN J M，ABASCAL R.Numerical simulation of Lamb wave scattering in semi-infinite plates［J］.Int J. Num.Meth.Eng.，2002，53（5）：1145-1173.

［11］KE W，CASTAINGS M，BACON C.3D finite element simulations of an air-coupled ultrasonic NDT system［J］. NDT&E International，2009，42（6）：524-533.

［12］CASTAINGS M，CAWLEY P.The generation，propagation，and detection of Lamb waves in plates using aircoupled ultrasonic transducers［J］.J.Acoust.Soc.Am.，1996，100（5）：3070-3077.

The numerical simulation of the excitation and detection of Lamb waves using air-coupled ultrasonic phased array with finite element method

ZHANG DiWU Xianmei
（State Key Laboratory of Acoustics，Institute of Acoustic，Chinese Academy of Sciences，Beijing 100190，China）

The non-contact air-coupled ultrasonic transducer and its use in non-destructive testing methods have been greatly advanced recent years.It has been used in the testing of thin plate，fiber-reinforced composite plate，laminated structure and bonding strength testing.However，due to the limitation nature of the air-coupled ultrasonic detection，the problem remaining is how to improve the transmitting and receiving efficiency and sensitivity.In this paper，an air-coupled capacitive ultrasonic phased array has been proposed for the enhancement of the efficiency.The finite element method is used to explore the dynamic transmitting characterization of a 1D linear phased array.The acoustic fields in air transmitted by the ultrasonic array are calculated and analyzed.The displacement fields in plate excited by the ultrasound are calculated and monitored.Lamb waves in plate are excited and then received in this model.Several Lamb wave modes，i.e. A0and S0are excited based on the dynamic scanning along the plate surface.This model could be used in the simulation of the air-coupled ultrasonic Lamb wave testing of a plate.

Air-coupled ultrasonic transducer，Non-destructive testing，Lamb waves excitation，1D linear phased array，Finite element simulation

O426.9

A

1000-310X（2015）03-0201-06

10.11684/j.issn.1000-310X.2015.03.003

2014-12-17收稿；2015-01-28定稿

∗国家自然科学基金项目（11274337）

张迪（1985-），男，山东巨野人，助理研究员，博士，研究方向：超声换能器与检测技术。†

E-mail：d.zhang@mail.ioa.ac.cn