多通道超声兰姆波检测板状结构中的裂纹∗
2015-10-26张正罡他得安
张正罡 刘 丹 他得安†
(复旦大学电子工程系 上海 200433)
⋄2014年度全国检测声学会议优秀论文专栏⋄
多通道超声兰姆波检测板状结构中的裂纹∗
张正罡刘丹他得安†
(复旦大学电子工程系上海200433)
超声兰姆(Lamb)波在结构缺陷检测方面愈来愈受到重视,但目前Lamb波的应用局限于单信号源激励,单通道接收的方法,容易受到噪声干扰,其后续的信号分析处理也比较复杂。本文旨在采用多通道Lamb波对板状结构中的裂纹进行定量分析与诊断。在铝板的表面凿刻出不同深度的凹槽作为裂纹,通过线阵换能器采集在一定传播距离内的多通道Lamb波信号,并采用二维傅里叶变换分析在不同深度的裂纹下,Lamb波模式能量的变化规律。结果表明,相对于完好铝板中的Lamb波信号,裂纹的存在会使Lamb波发生模式转换现象,并且转换模式能量百分比随裂纹深度的增加而线性增加。其结果为Lamb波评价板状结构中的裂纹状况提供了一种可能的方法。
Lamb波,裂纹,多通道,模式转换
1 引言
超声波是目前广泛应用的结构损伤检测手段之一。超声波的传播特性与介质的弹性特征、微观结构等密切相关,通过提取和分析超声波信息,可评估介质的结构和性能。尤其对于大型板状或管状介质,超声导波可沿轴向传播较远的距离,且声场遍及整个厚度方向。在有限接收位置采集到的超声导波信号就能够反映整个传播范围内介质的特性,这与传统超声的逐点扫描法相比,具有快速、高效等优点,已成为近年来无损检测领域的研究热点[1-4]。ROSE J L等[5]在理论上求解了规则形状波导(板状、管状等)中超声导波的频散方程,并指出超声导波的多模式特性。相应的导波多模式分离算法也相继被提出来分离出单一的导波模式[6-8]。他得安等[9-10]分析了板中导波的位移分布特点,为在实际应用中选择何种模式的导波提供参考。张正罡等[11-12]实验观察了在离体长骨样本中的非线性超声导波,发现基频导波所激励出的二次谐波的幅度随传播距离的增加而增加。
裂纹是导致众多材料和结构失效的主要原因,超声Lamb波在裂纹检测方面的研究也受到极大关注[13]。SHIN H J等[14]指出(兰姆)Lamb波在裂纹处会发生不同模式相互转换的现象。SANTHANAM S等[15]提出可用Lamb波在板中遇到裂纹时的反射与透射系数来定量评价裂纹深度。TASHI S等[16]采用有限元法对裂纹板中Lamb波进行仿真,得出透射Lamb波能量会随裂纹长度的增加而减少。XU K等[17]在时域上对转换模式信号进行分离,并发现转换模式能量随裂纹深度呈正相关。但目前,Lamb波在裂纹检测领域的应用,局限于单信号源激励,单通道接收的方法,容易受到噪声干扰,其后续的信号分析处理也比较复杂。本文在一系列不同深度裂纹的铝板上,通过线阵换能器接收在一定距离范围内的多通道Lamb波信号,并利用经典二维傅里叶变换把Lamb波信号从距离-时间域变换至相速度-频率域,通过计算透射Lamb波中原始模式与转换模式能量百分比,来定量分析其与裂纹深度的关系。
2 超声Lamb波理论
对于厚度为2h的单层自由板状结构,受控于运动方程和边界条件,导波问题的求解可表示为

其中w为角频率,k为波数,cL为纵波速度,cT为横波速度。方程(1)描述的是对称Lamb波模式(记为Sn模式,n=0,1,2,···为模式阶数),方程(2)为反对称Lamb波模式(记为An模式,n=0,1,2,···为模式阶数)。求解方程(1)和(2),可得到角频率w与波数k表示的Lamb波模式的理论频散曲线,再由式k=w/cp可将频散曲线转化为角频率w和相速度cp的关系。
3 二维傅里叶变换
二维傅里叶变换是有效测量Lamb波频散曲线的一种方法,它将不同传播距离下的多通道Lamb波时间信号转换为波数-频率的形式,从而识别出各个单一模式的Lamb波。设多通道Lamb波为r(x,t),其中x为传播距离,t为传播时间,则二维傅里叶变换可表示为[18]
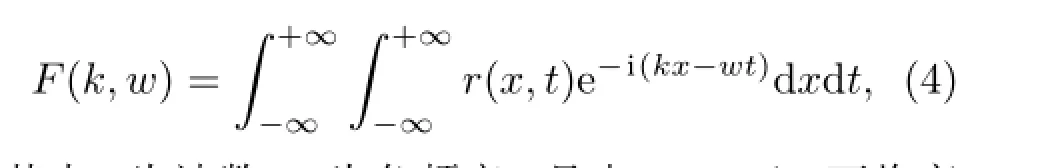
其中k为波数,w为角频率。且由k=w/cp可将变换结果转化为相速度cp和角频率w的关系。二维傅里叶变换的优点在于可同时得到Lamb波的相速度和幅值大小。文中将相速度的结果与理论相速度频散曲线进行匹配,以识别不同模式的Lamb波。而将幅值作为衡量不同模式Lamb波能量大小的标准。
4 实验设计
采用厚度分别为3 mm、4 mm和5 mm的一系列铝板作为实验样本。铝板材料的密度为2700 m/s,横波速度为3130 m/s,纵波速度为6320 m/s。在铝板的下表面凿刻出宽度为1 mm,不同深度的横穿矩形凹槽作为裂纹。其中3 mm系列铝板的裂纹深度为0.5 mm~2.5 mm;4 mm铝板的裂纹深度为0.5 mm~3.5 mm;5 mm铝板的裂纹深度为0.5 mm~4 mm。裂纹深度的间隔均为0.5 mm。图1为厚度为3 mm,裂纹深度为0.5 mm至2.5 mm的铝板样本实物图。
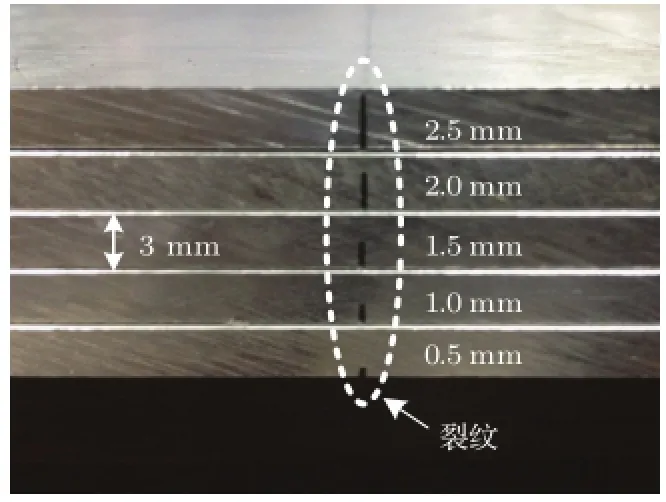
图1 3 mm铝板样本实物图Fig.1 Photo of 3 mm aluminum plate
实验采用轴向传输法测量铝板中的多通道Lamb波信号,图2为实验装置框图。发射换能器(AT014,Valpey-Fisher,MA,USA)和接收线阵换能器(P4-1,Bothell,WA,USA)分别置于铝板的上表面,裂纹的左右两侧,二者的中心位置距裂纹均为30 mm。发射换能器的中心频率为1 MHz,并置于倾斜角为45°的斜块上。激励源为中心频率2 MHz,15周期的正弦信号,由任意波形发生器(33220A,Agilent,CA,USA)产生,经过放大后输入到发射换能器。铝板中的Lamb波传播遇到裂纹时,会发生模式转换现象,实验未考虑在裂纹处的反射Lamb波,只由接收线阵换能器采集在一定范围内铝板上表面的多通道透射Lamb波信号。经由多通道超声接收仪(Vantage-128,Verasonics,WA,USA)接收后并转换为数字信号,存入计算机以作进一步处理。接收换能器的-3 dB频带范围为1.0 MHz至4.0 MHz,共96个通道,相邻通道的间隔为0.25 mm。
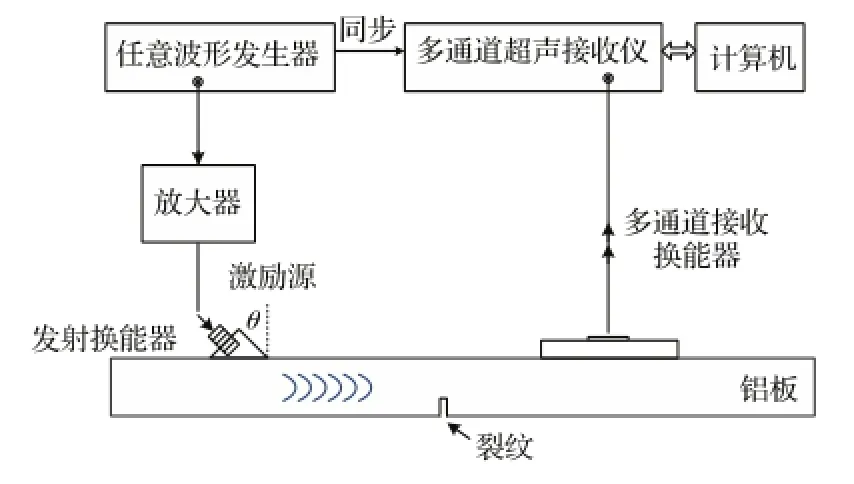
图2 实验装置框图Fig.2 Block diagram of experiments
5 结果与讨论
以厚度为5 mm的铝板为例,图3为铝板上表面传播距离为48 mm~72 mm的多通道Lamb波距离-时间图,其中图3(a)为完整无裂纹铝板中的Lamb波信号,图3(b)为裂纹深度为3 mm铝板中的Lamb波信号。相对于完整铝板,存在裂纹铝板中的Lamb波更为散乱。采用二维傅里叶变换将Lamb波信号从距离-时间域变换至波数-频率域,并进一步将波数转化为相速度。图4中,伪彩色为不同深度裂纹铝板中Lamb波相速度-频率域表示,三条曲线表示由式(1)和式(2)计算求得的相速度理论频散曲线。其中图4(a)为完整铝板;图4(b)、4(c)、4(d)和4(e)分别为1 mm、2 mm、3 mm和4 mm裂纹深度的铝板。由图4(a)可知,在完整铝板中,Lamb波信号主要为S2模式和极少量的A3模式。而在有裂纹的铝板中,Lamb波在裂纹处发生了模式转换现象。在图4(b)中,1 mm深度的裂纹使部分S2模式的能量转移到A3模式。当裂纹深度为2 mm时,S2模式的更多能量转移到A3模式,并且出现了少量的A2模式。本文中,将完整铝板中主要存在的S2模式作为原始模式,而把A2和A3模式作为转换模式来进行讨论。当裂纹深度增加至3 mm时,原始模式S2的能量进一步降低,而转换模式A2和A3的能量则随之升高。最后,到裂纹深度达到4 mm时,Lamb波中能量最高的模式为转换模式A3,原始模式S2次之,另外一个转换模式A2的能量相比与3 mm裂纹时的能量也有所增加。
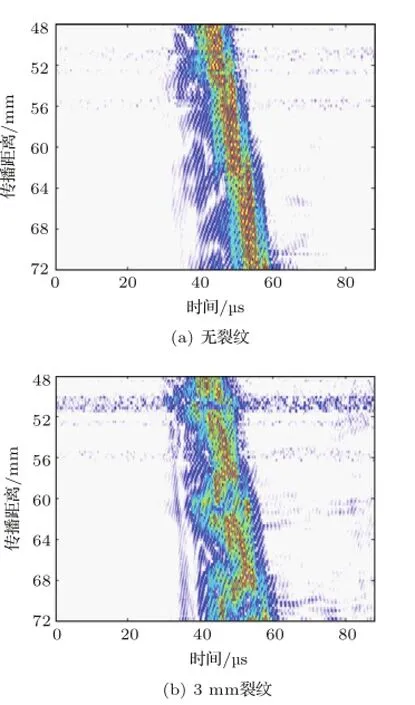
图3 5 mm铝板中多通路超声Lamb波距离-时间图Fig.3 Distance-time plot of multi-channel ultrasonic Lamb wave in 5 mm aluminum plate
为定量分析不同深度裂纹中的Lamb波原始模式与转换模式的能量关系,在相速度-频率表示域中,分别计算各个模式对应区域的能量。并统计原始模式S2和转换模式(包括A2和A3模式)所占Lamb波总能量的百分比,以降低测量条件以及在裂纹处的反射Lamb波对结果造成的影响。由于转换模式A2和A3各自的能量百分比与裂纹深度的关系较为复杂,本文把A2和A3作为统一的转换模式来讨论。图5为S2以及转换模式所占能量比与裂纹深度之间的关系,直线为对应的线性拟合结果。图5(a)、图5(b)和图5(c)分别是3 mm、4 mm和5 mm厚度铝板中的结果,直线拟合的相关性分别为0.911、0.867和0.986。以5 mm铝板为例,可以看到,在完整铝板中Lamb波主要为原始模式,而随着裂纹深度的增加,原始模式所占能量比线性下降,其能量逐渐转移到转换模式,转换模式能量线性上升。当裂纹深度约为2.8 mm时,原始模式与转换模式能量各站总能量的50%。当裂纹深度增加至4 mm时,转换模式的能量百分比为67.5%,而原始模式则降低为32.5%。
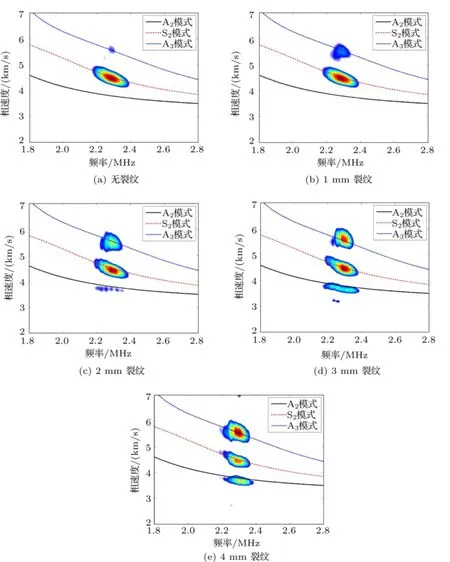
图4 5 mm铝板中多通道Lamb波相速度-频率图Fig.4 Wavenumber-frequency plot of multi-channel ultrasonic Lamb wave in 5 mm aluminum plate
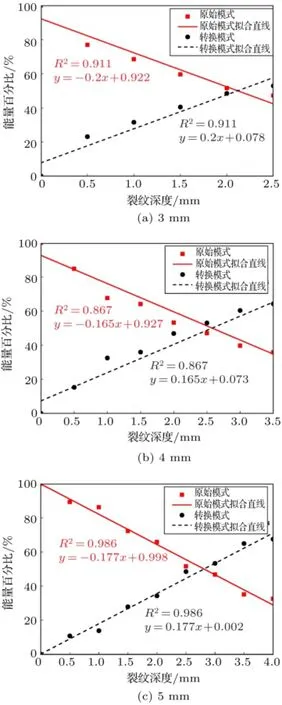
图5 原始模式S2与转换模式能量百分比与裂纹深度的关系Fig.5 Relationship between energy percentages of original S2and converted modes with crack thicknesses
值得注意的是,Lamb波遇到裂纹时发生的模式转换现象非常复杂,本文通过优化实验条件,使得完整铝板中的Lamb波主要为单一的模式,进而在裂纹深度逐渐增加时,讨论该单一Lamb波模式能量的变化情况,极大的简化了模式转换现象的分析,使得利用透射Lamb波来评价裂纹状况有一定的实际意义。
6 结论
本文以一系列不同深度裂纹铝板为实验样本,定量分析了Lamb波在经过裂纹时不同模式之间能量转移的现象。对由线阵换能器接收到的多通道Lamb波信号,进行二维傅里叶变换将其转化到相速度-频率域,用以识别原始Lamb波模式以及转换Lamb波模式,并进一步计算原始模式和转换模式所占总能量的百分比与裂纹深度的关系。结果表明,相对于完整铝板,存在裂纹铝板中的Lamb波在遇到裂纹时会发生模式转换现象,部分原始模式的能量会转移到转换模式。原始模式的能量百分比随裂纹深度的增加而线性下降;反之,转换模式的能量百分比随裂纹深度的增加线性上升。当裂纹深度接近于整个铝板厚度时,转换模式的能量会超过原始模式。本文的结果有助于应用Lamb波来评价板状结构中的裂纹状况。
[1]SU Z,YE L.Identification of damage using Lamb waves:from fundamentals to applications[M].Berlin:Springer,2009.
[2]刘镇清.无损检测中的超声兰姆波[J].无损检测,1999,21(9):410-423.
LIU Zhenqing.Ultrasonic Lamb waves in nondestructive testing[J].Nondestructive Testing,1999,21(9):410-423.
[3]罗宏建,周重回,王炯耿,等.铝制焊接容器超声导波成像检测[J].应用声学,2014,33(6):520-527.
LUO Hongjian,ZHOU Chonghui,WANG Jionggeng,et al.Ultrasonic guided waves imaging testing on aluminum welded shell[J].Journal of Applied Acoustics,2014,33(6):520-527.
[4]陈军,李志浩,林莉,等.铝板中Lamb波检测的实验研究[J].应用声学,2011,30(2):98-104.
CHEN Jun,LI Zhihao,LIN Li,et al.Experiment investigations of Lamb waves in an aluminum plate[J].Journal of Applied Acoustics,2011,30(2):98-104.
[5]ROSE J L.Ultrasonic waves in solid media[M].UK:Cambridge University Press,1999.
[6]SONG X,Ta D,WANG W.Analysis of superimposed ultrasonic guided waves in long bones by the joint approximate diagonalization of eigen-matrices algorithm[J].Ultrasound in Medicine&Biology,2011,37(10):1704-1713.
[7]XU K,TA D,WANG W.Multiridge-based analysis for separating individual modes from multimodal guided wave signals in long bones[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,2010,57(11):2480-2490.
[8]XU K,TA D,MOILANEN P,et al.Mode separation of Lamb waves based on dispersion compensation method[J]. Journal of the Acoustical Society of America,2012,131(4):2714-2722.
[9]他得安,刘镇清,贺鹏飞.复合管状结构中超声导波的位移分布[J].复合材料学报,2003,20(6):131-136.
TA Dean,LIU Zhenqing,HE Pengfei.Displacement distribution of longitudinal guided waves in composite pipes[J].Acta Materiae Compositae Sinica,2003,20(6):131-136.
[10]TA D,WANG W,WANG Y,et al.Measurement of the dispersion and attenuation of cylindrical ultrasonic guided waves in long bones[J].Ultrasound in Medicine&Biology,2009,35(4):641-652.
[11]ZHANG Z,LIU D,DENG M,et al.Experimental observation of cumulative second-harmonic generation of Lamb waves propagating in long bones[J].Ultrasound in Medicine&Biology,2014,40(7):1660-1670.
[12]DENG M.Cumulative second-harmonic generation of Lamb-mode propagation in a solid plate[J].Journal of Applied Physics,1999,85(6):3051-3058.
[13]郑阳,何存富,周进节,等.超声兰姆波斜入射裂纹时的散射特性[J].机械工程学报,2013,49(a):6-12.
ZHENG Yang,HE Cunfu,ZHOU Jinjie,et al.Scattering characteristic of Lamb wave at crack with oblique incident[J].Journal of Mechanical Engineering,2013,49(a):6-12.
[14]SHIN H J,SONG S.Observation of Lamb wave mode conversion on an aluminum plate[C].15thWorld Conference on Nondestructive Testing,2000.
[15]SANTHANAM S,DEMIRLI R.Reflection and transmission of fundamental Lamb wave modes obliquely incident on a crack in a plate[C].IEEE International Ultrasonics Symposium Proceedings,2012:2690-2693.
[16]TASHI S,ABEDIAN A,KHAJEHTOURIAN.The finite element simulation of Lamb wave propagation in a cracked structure with coupled filed elements[J].Advanced Materials Research,2012,463-464:618-623.
[17]XU K,TA D,SU Z,et al.Transmission analysis of ultrasonic Lamb mode conversion in a plate with partialthickness notch[J].Ultrasonics,2014,54(1):395-401.
[18]ALLEYNE D,CAWLEY P.A two-dimensional fourier transform method for the measurement of propagating multimode signals[J].Journal of the Acoustical Society of America,1991,89(3):1159-1168.
Detection of crack in plate structure using multi-channel ultrasonic Lamb waves
ZHANG ZhenggangLIU DanTA Dean
(Department of Electronic Engineering,Fudan University,Shanghai 200433,China)
Utilizing ultrasonic Lamb waves to detect cracks in plate structures has been an important technique in non-destructive testing(NDT)area.However,up to now,most practical applications just use one source to excite and one receiver to obtain Lamb wave signals,which is susceptible to noise.Besides,the one channel signal processing method is usually complex because of the multi-mode and dispersion characteristics of Lamb waves.The object of this study is using multi-channel ultrasonic Lamb waves to quantitatively evaluate cracks in aluminum plates.Notches with various depths were curved out from the aluminum plate to regard as cracks.The multi-channel Lamb waves were collected in a certain propagation distance range through linear array transducer.The relationship between energy of different Lamb wave modes and the depth of crack was analyzed using two dimensions Fourier transform(2DFT).Results show that comparing to the intact aluminum plate,new Lamb wave modes would occur due to exist of cracks.And,the energy percentage of converted modes increases linearly with the depth of crack.This study may provide a rapid and reliable method to evaluate the crack condition in plate structures.
Lamb waves,Crack,Multi-channel,Mode conversion
O426.2;O426.9
A
1000-310X(2015)03-0189-06
10.11684/j.issn.1000-310X.2015.03.001
2015-01-15收稿;2015-03-17定稿
∗国家自然科学基金(11174060,11327405),上海市科技支撑计划(134419011900),教育部博士点基金资助项目(20130071110020)
张正罡(1990-),男,陕西榆林人,博士研究生,研究方向:医学超声信号处理。
E-mail:tda@fudan.edu.cn
