被动线谱检测的子带分解和分方位区间融合算法∗

戴文舒†　陈新华　孙长瑜

（1中国科学院声学研究所　北京　100190）

（2中国科学院大学　北京　100049）

⋄研究报告⋄

被动线谱检测的子带分解和分方位区间融合算法∗

戴文舒1，2†陈新华1孙长瑜1

（1中国科学院声学研究所北京100190）

（2中国科学院大学北京100049）

目标辐射噪声低频线谱丰富，线谱相对谱级高，且较稳定，可直接应用于目标检测。基于子带分解处理的现有融合方法适用于信噪比相对较高情况，而对于相干干扰噪声或强宽带噪声，线谱目标的有效检测仍没很好解决。本文从子带空间谱统计特性出发，利用线谱谱级高出连续谱10～25 dB，线谱频带所在方位区间的输出方位波动小，而其它分区间的输出方位波动大的特点，提出了一种在信噪比低，多目标并存情况下更有效的线谱提取融合方法。理论仿真和海试实验数据处理结果验证该算法较常规方法稳定，对于高谱级线谱，算法适用范围广、检测效果好，直观、简便，为实际工程应用提供了一种新方法。

低频线谱检测，信息融合，子带分解，分方位信号处理

1　引言

上世纪70年代以来，具有大型基阵的被动声纳普遍采用了线谱检测技术。对于一定的深度和航速，舰船噪声功率谱存在一个临界频率，一般在100～1000 Hz之间，低于此频率主要是机械噪声和螺旋桨噪声线谱，高于此频率主要是空化产生的宽带连续谱，对舰船噪声线谱的测量表明，其强度有时可高于附近连续谱10～25 dB，且稳定性高［1-2］。舰船辐射噪声的包络线谱（调制线谱）是一个重要特征，对发现和识别目标有重要作用，这是因为包括螺旋桨在内的船用机械设备转动时，对空泡脉冲、桨叶负荷脉冲或其它脉冲型激励激发的壳体振动等宽带噪声产生周期性作用［3］，这种乘性调幅的频率与轴频，叶片频相对应。但各频带上调制深度的分布等，需要从时变谱或双重谱了解规律性特征［4-6］。螺旋浆转动时对随机序列脉冲宽带噪声作周期性调制，辐射低频线谱［3］，解调后谱分析即DOMEN低频线谱，通过其二阶循环统计量分析即获直接辐射低频线谱。文献［7］从求解背景噪声中检测包络线谱所需的最小可检测信号角度，估算了高斯背景中检测舰船噪声中周期调制的性能。文献［8］给出包络线谱相对于连续谱的信号高度衰减规律，大信噪比下几乎不衰减，小信噪比下随信噪比的平方衰减。文献［9］从调制谱和低频线谱在信噪比减小时，其相对幅度的下降速度这一角度进行对比分析，得出低频线谱在相同可检测最小信号前提下，其随信噪比减小而下降的相对幅度总是低于调制谱。

鉴于低频线谱检测的优越性，国内已有一些学者对未知线谱的目标检测问题展开研究。在信噪比相对较高情况下，对频域分频带处理的每个频率单元做波束形成，利用干扰噪声频率单元方位估计结果随机，其均值趋于零，而目标线谱方位估计结果具有确定性，其均值为某一定值的特点，对线谱频率和干扰噪声频率所作的多次方位估计结果进行方位统计平均，实现对目标的检测［10-11］。文献［12］分析了多目标干扰严重时，近处强目标给检测远程弱目标带来困难，但当目标线谱的谱级足够高时，文中算法仍旧可以实现检测。然而上述融合算法在弱目标信噪比进一步下降或存在相干干扰时，各频率单元方差权值的误差会变大，对目标的有效检测仍未很好解决。本文将研究高斯背景噪声中高强度稳定线谱目标经过频域分频带波束形成后，各子带分方位区间的方位统计方差特征、空间谱累加特征，以及峰均比统计特征，在此基础上提出一种基于子带分解和分方位区间统计的未知线谱融合算法，并仿真研究多干扰情况下线谱目标的检测性能，以及方位区间对目标检测性能的影响。最后，以海试数据处理结果验证这一新算法的有效性。

2　子带分解统计融合的未知线谱检测理论

2.1阵元接收模型

设含某频率线谱的海洋舰船辐射噪声为

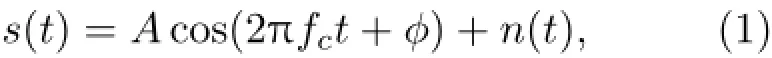
式中A为线谱幅值，fc为未知线谱频率，φ为均匀分布的随机相位，n（t）为宽带连续谱噪声。舰船线谱与连续谱的谱级比为10～25 dB。阵元接收信号模型如文献［13］，舰船目标方向为θ0。

2.2空间谱的特征分析

基阵接收到的信号经前置滤波，降采样处理后，经FFT变换到频域，分频带作常规波束形成（CBF）处理后得到每个频率单元的空间谱，由背景噪声的非平稳性以及低频传播衰减弱的特点，进行N次统计，基于未知线谱目标谱级高于连续谱谱级，而且统计时间内目标方位变化缓慢。位于θ0方位的上述线谱目标有以下特点：

（1）信噪比较高时，目标线谱fc单元的方位输出为空间谱在整个区间上最大谱值对应的方位，稳定性好，N次输出结果都聚集到信号方位θ0。

（2）信噪比较高时，目标线谱fc单元N次方位输出的统计方差δθ与其他噪声频率单元的方差相比是最小的。

（3）信噪比下降时，一次处理中目标线谱fc单元方位输出在整个方位区间上波动大，而且输出方位上的空间谱值有可能不是所有频带单元中最大的。

图1是信噪比低情况下，线谱频带一次波束输出的空间谱，线谱目标位于125°正方形标记处，若在整个方位区间上按照传统方位稳定性算法进行方位方差的统计，那么线谱频率单元的统计方差和噪声频带各单元的方差相近，不能充分利用信号信息，容易丢失目标。图2给出线谱所在频带N次空间谱叠加的结果，线谱目标所在方位125°对应的空间谱输出显著增高。

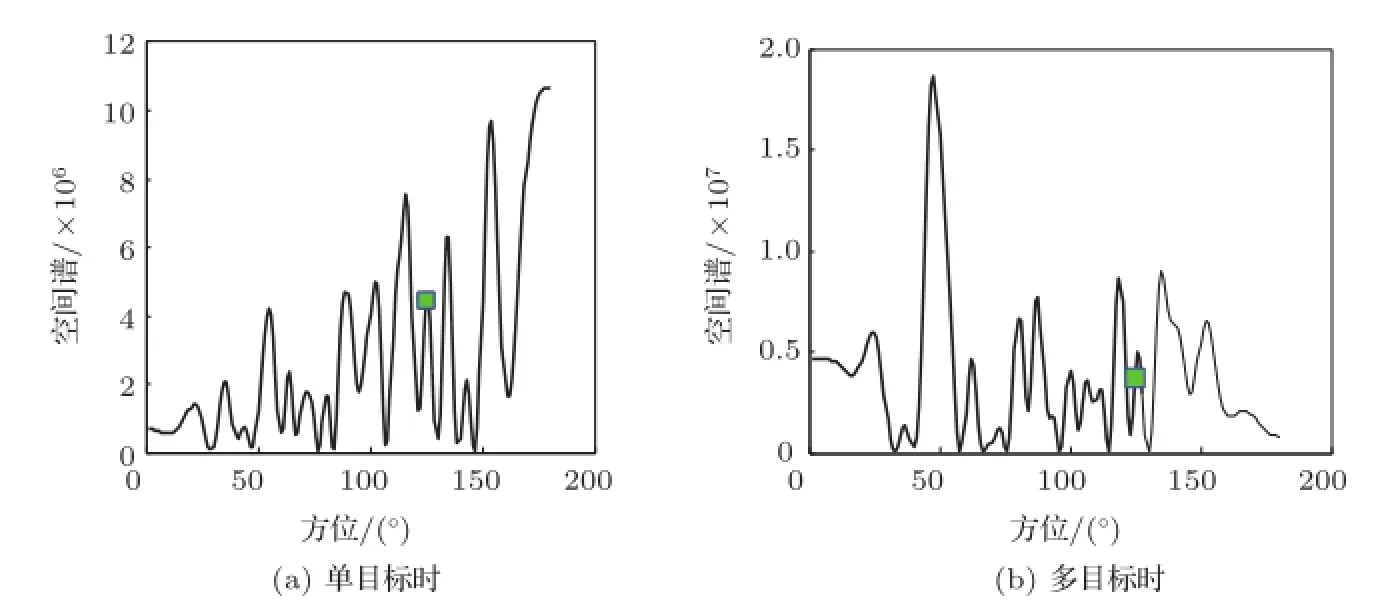
图1　信噪比低情况下目标线谱频带一次波束输出的空间谱Fig.1 One result of spatial spectrum in target frequency band when SNR is low

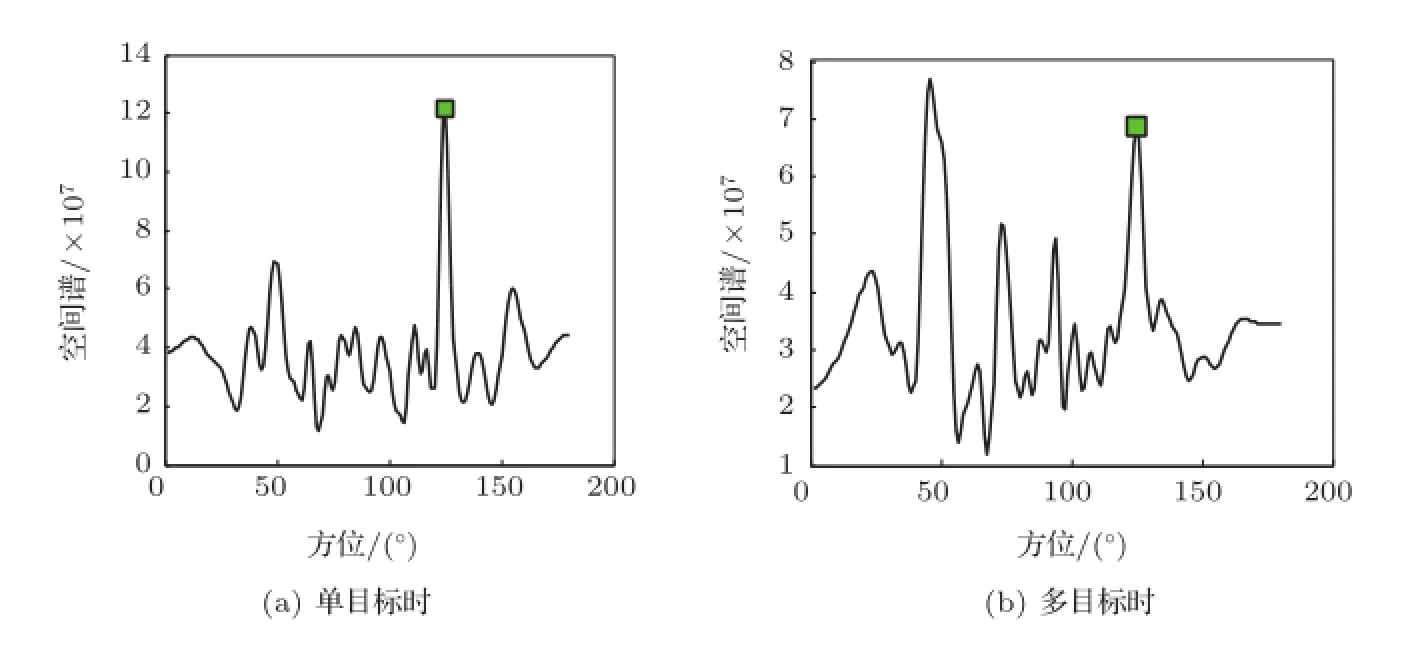
图2　信噪比低情况下目标线谱频带N次叠加后的空间谱Fig.2　Result of spatial spectrum after the superposition of N times in target frequency band when SNR is low

当存在相干干扰或宽带强干扰时，为了使整个区间的方位统计值方差变差这一状况得到改善，本文依据图2所示特性，提出一种子带分解和分方位区间统计融合方法，将整个区间划分为K个区间，有以下特征：

（1）目标线谱fc单元，每个区间上的空间谱值的最大值对应方位记为该区间上的方位输出，统计N次，记为θij，i=1，···，K；j=1，···，N；线谱目标方位θ0所在的区间上的统计方差相比于其它区间是最小的；

（2）各频率单元作区间划分，区间上空间谱值最大值在该区间上所有极大值中最大的，若该区间没有极大值，最大值输出对应方位选择在区间端点处；

（3）存在宽带强干扰情况下，并且谱级小于目标线谱的谱级，强干扰方位所在区间的N次统计方差与其他K-1个区间的统计方差相比较小。

下面基于分区间的方差特征和分频带的空间谱特征融合，给出具体算法流程。

3　子带分解和分方位区间统计融合的未知线谱检测算法

设子带个数为M个，记作fp，p=1，···，M，波束预成方位180个，记为θq，q=1，···，180。连续处理N帧数据信号，按以下算法处理，每个频率单元的波束输出记为R（fpj，θqj），j=1，···，N：

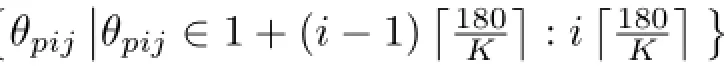
步骤2：重复步骤1，连续处理N帧，同时按公式（2）累加第i区间，i=1，···，K上N次波束输出的空间谱。最终得到NMK个谱值和方位值以及累加后的空间谱SumN（p，i）。

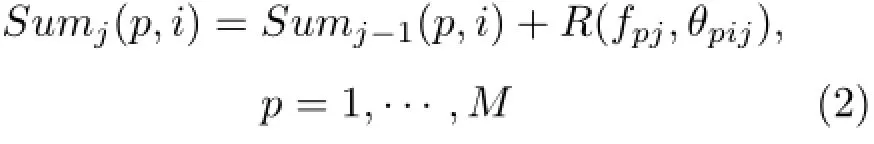
步骤3：每个子带，对K个区间分别处理。在每个区间，保存步骤1累加后的空间谱SumN（p，i）最大谱值及其方位，记作Rmax（p，i）和ˆθmax（p，i），p=1，···，M；i=1，···，K，得到MK个谱值和方位值。

步骤4：每个子带，对K个区间分别处理。在每个区间，将步骤2中保存的N个方位判断野值，去除野值。

步骤5：每个子带，对K个区间分别处理。在每个区间，计算并保存步骤4保留的方位的方差，方差计算采用公式（3）计算，均值为步骤3中保存的该区间的方位。采用步骤2中叠加谱归一化结果Q（ˆθpij）对保留的方位的方差贡献加权，如目标线谱频率fcHz的观测［123°，121°，134°，125°，124°，129°］，由步骤1计算的归一化结果为［0.6，0.3，0.1，1，0.8，0.2］。那么θ0=125°对方差计算的贡献大，这样便减少了线谱频带的方差。

步骤6：计算M个子带，各自K区间的输出。区间方位输出为步骤3的保存的方位，区间的空间谱输出为步骤3保存的谱值。

步骤7：计算子带输出。每个子带，提取K个区间输出谱值中大于半功率点的所有区间，保存这些区间中按步骤5中计算的方差中最小的3个区间作为该子带的输出区间。这3个区间的空间谱谱值和方位值就是该子带的输出。

步骤8：比较M个子带所有输出区间的空间谱值，提取大于最大谱值0.717倍的所有子带。若其中Mp1，Mp2两子带的有相同的输出方位，则取步骤5保存的该方位下较小的方差所在的子带的输出作为最终该方位下的空间谱值Pout。

步骤9：将步骤8的融合输出结果用最大值Pmax和非零值中最小值P¯0按下列公式归一。

信号检测流程示意于图3。

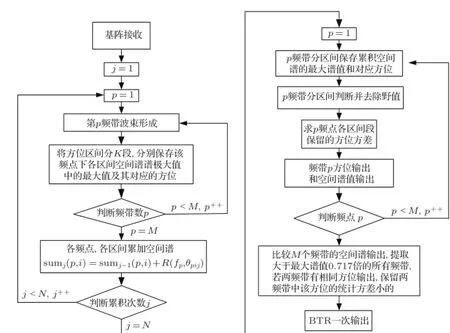
图3　基于子带分解和分方位统计融合的未知线谱检测流程图Fig.3 The flow chart of fusion algorithm for detecting the target of linespectrum based on the sub frequency and sub interval statistics

4　子带分解和分方位区间统计融合的未知线谱检测算法理论仿真

4.1多目标条件下的检测性能

仿真条件：设目标线谱频率，线谱与连续谱谱级比为18 dB。采用均匀线列阵处理。阵元个数32，阵间距8 m，连续处理10帧信号，每帧1 s，分方位区间9个，1°—20°，21°—40°，···，161°—180°。在信噪比为-30 dB情况下，有信干比为-13 dB的非同向强高斯噪声干扰“目标”，二者落入不同的方位区间，线谱目标位于125°，强干扰目标位于50°。单个水听器接受信号和线谱目标辐射功率谱图如图4所示。

图5（a）采用对文献［9］改进的方位稳定算法，该文第4节中算法步骤（4）计算每个子带统计方位方差时，该频带N次累加波束输出谱中最大值为R（fp，θp，m），p=1：M，对应的方位记为θp，m，作为计算方差的均值。每帧波束输出谱值前3个极大值记为R（fp，θp，x），x=1，2，3，对应的方位θp，x，x=1，2，3。|R（fp，θp，x）-R（fp，θp，m）|最小的方位作为该子带的方位输出。图5（b）除50°的强干扰目标外，隐约有125°的弱线谱目标，而在图5（c）中，可明显看到125°存在目标，本文算法有效的提取了弱线谱目标。

4.2落入不同方位区间的多目标检测性能

当信噪比为-30 dB，分方位区间9个同上，声纳视野中有三个运动目标，即线谱目标和2个强干扰目标，彼此不在同一个区间：干扰1的信干比-13 dB，位于50°；干扰2的信干比为-10 dB，位于70°；线谱目标位于130°。其他处理条件同4.1节。

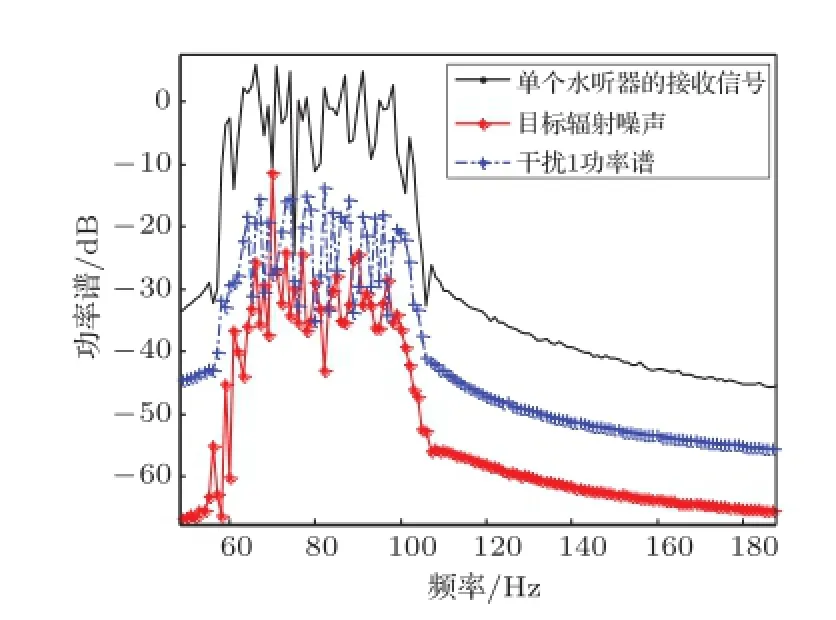
图4　单个水听器接收信号和目标辐射信号功率谱Fig.4 Signal received by single hydrophone and the power spectrum of signal radiated by target

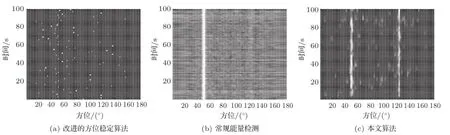
图5　存在强干扰目标时，弱线谱的提取算法对比Fig.5 Contrast of weak line spectrum extraction algorithms under the strong target interference

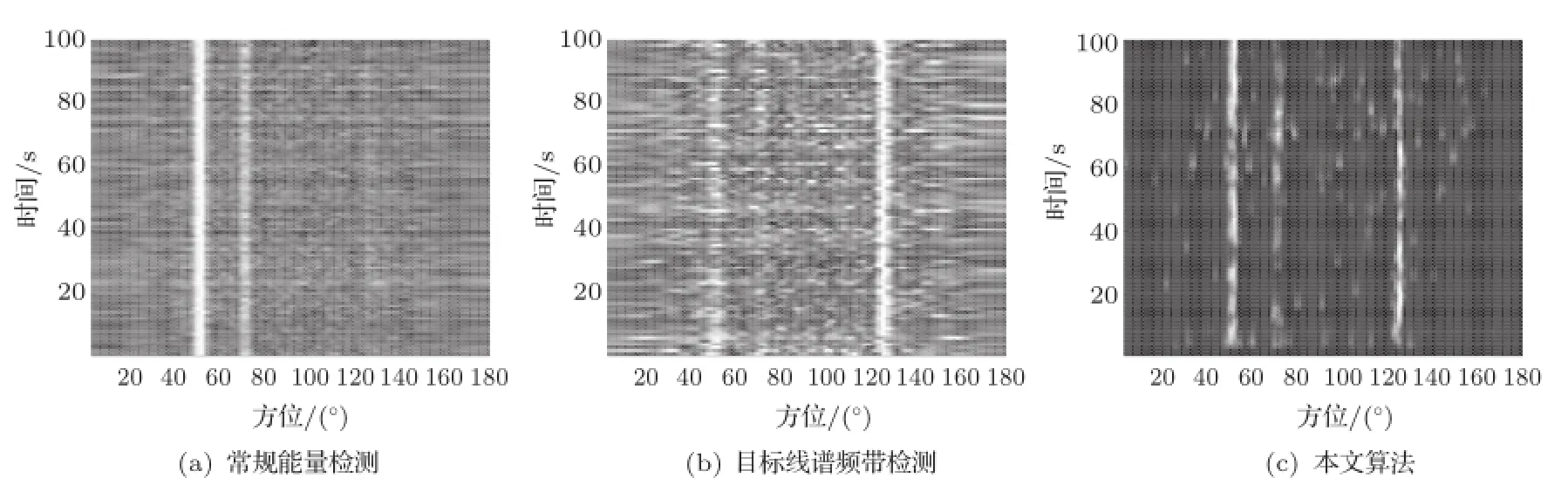
图6　3个目标落入不同方位区间时，弱线谱目标检测Fig.6 Contrast of weak line spectrum detection when targets are located in different subintervals

图6（a）可明显检测到分别位于50°和70°方位的两强干扰，图6（b）图是线谱子带的检测结果，线谱谱级高而且稳定，图6（c）是采用本文融合算法后的检测结果，因为此方法步骤8中涉及门限选择，合理调整门限可以同时检测到三个目标。

4.3线谱目标和强干扰位于同一方位区间的检测性能

声纳视野中有三个运动目标，其中线谱目标和较强干扰“目标”位于同一个方位区间，方位分别为125°和135°，而另一干扰落入不同区间，方位是70°，其他处理条件同4.2节。图7（a）常规能量检测，位于125°的弱线谱目标被淹没，但可明显检测到两强干扰目标；图7（b）是线谱频带的检测结果；图7（c）采用本文融合算法后检测结果，可以明显发现位于125°的弱线谱目标和位于135°的强干扰，70°方位的干扰同时可见。

4.4两干扰位于同一方位区间的检测性能

当两干扰目标位于同一区间而与线谱目标不同区间，其他处理条件同上。图8（a）常规能量积分下125°的弱线谱目标被淹没，50°和65°的强干扰清晰可见；图8（b）线谱频带检测下结果；图8（c）采用本文算法可以清晰检测到方位125°的弱线谱目标，落入同一区间的较弱的干扰则受影响，但依然可以检测到。图9中2个干扰目标方位相差仅10°时，本文算法无法区分这两干扰“目标”。

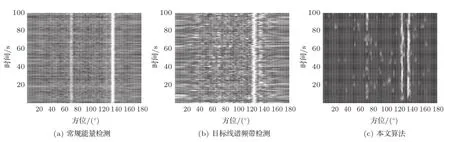
图7　弱线谱目标与某一强干扰位于同一方位区间时，线谱目标的检测Fig.7　Contrast of weak line spectrum detection when weak target and strong interference are located in the same subinterval

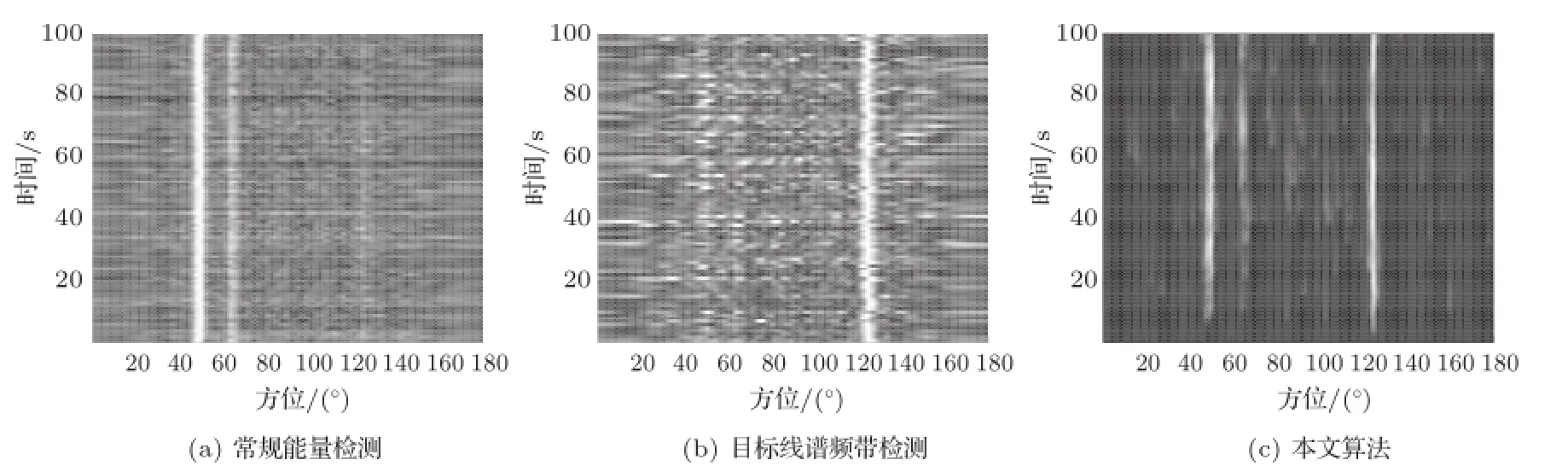
图8　干扰落入同一方位区间下的弱线谱目标检测Fig.8 Contrast of weak line spectrum detection when interferences are located in the same subinterval

5　实验数据处理和结果

下面将本文提出的基于子带分解和分方位区间融合检测弱线谱的方法，运用到实际海试实验数据处理中，通过海试数据的处理和分析进一步验证本文方法的有效性。该海试数据源于2012年在中国某水域的一次水声实验，实验期间水面弱线谱目标受海洋环境噪声和水面、水下其它目标的干扰等多种影响。既有近处强干扰抑制远处弱线谱目标的情况，又存在多干扰之间相互交叉，相互干扰的情况，与文中仿真条件相符。接收阵采用32元线列阵，带通前置滤波器带宽40 Hz，分40个频带处理，方位区间划分为19个，表1～表3记录了大约1200 s左右的一次统计，连续处理20帧，分别是每频带各区间方位方差统计特性，空间谱统计特性，峰均比统计特性。

图9　落入同一方位区间的2个干扰目标彼此方位太近时，目标检测性能Fig.9 Contrast of detection performance when targets in the same subinterval are too close

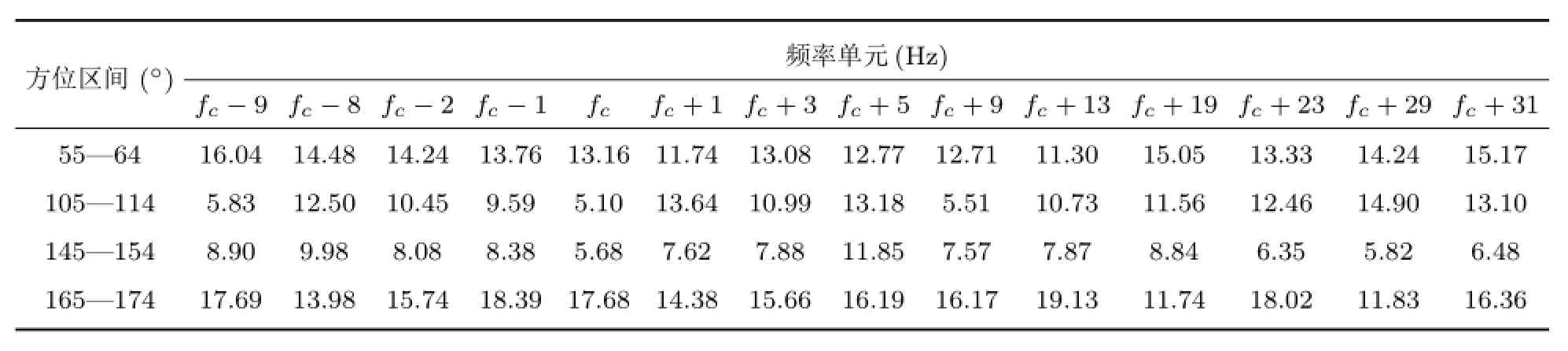
表1　子带分解、分方位区间算法方位方差统计特征Table 1　Statistical characteristic of orientation variance of algorithm based on sub frequency and sub interval statistic fusion

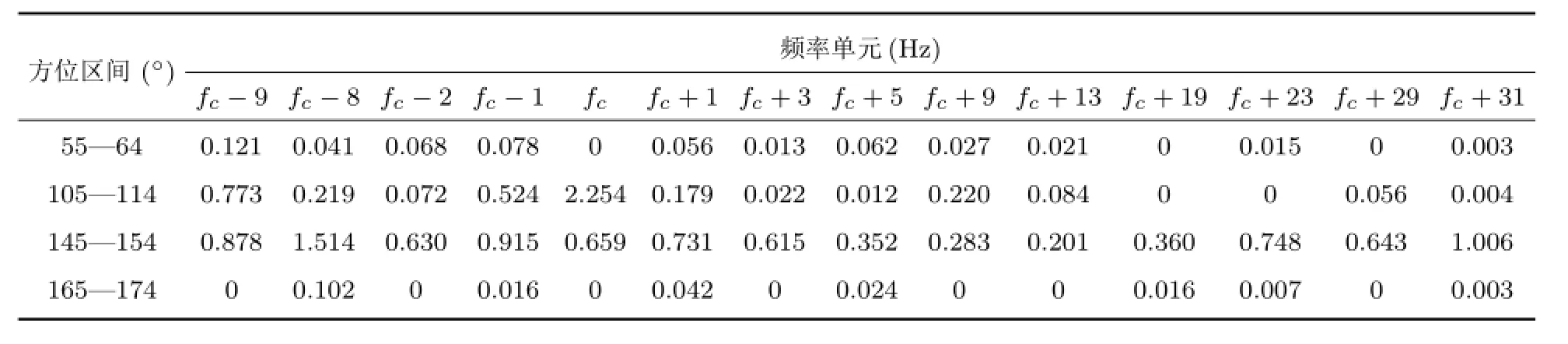
表2　子带分解、分方位区间算法空间谱极大值累加和统计特征（1.0×107）Table 2 Statistical characteristic of cumulative maximum value of spatial spectrum of algorithm based on sub frequency and sub interval statistic fusion

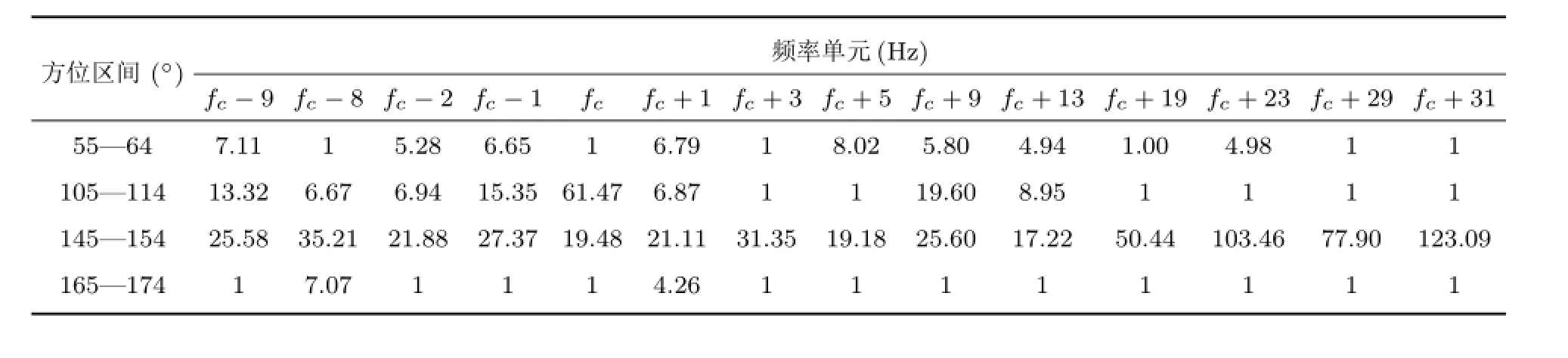
表3　子带分解、分方位区间算法空间谱峰均比统计特征Table 3 Statistical characteristic of peak to average ratio of algorithm based on sub frequency and sub interval statistic fusion

从图10（a）可以看到此时至少有3个运动目标，其中150°方向的干扰较强，而从图10（b）已知在110°左右存在线谱目标，而左图却被淹没。为了节约篇幅，方位区间列出几个特征区间，由于目标线谱此时位于110°左右，它所在区间上方位波动较小，而其他区间上方位波动较大；150°左右存在强宽带干扰，所以各频带率单元在它所在的区间的方位波动同样很小。从表1可以看出fc频率单元一列，区间105°～114°上方位方差是5.10，相比其他3个区间的方位方差较小。而145°～154°一行，各频率单元的方位方差都较小。其他频带和区间的统计方差相对较大。

表2代表对整个区间上保存前四个极大值，统计20次后计算分别落入每个区间的个数并累加极大值。实验表明落入目标线谱频带的极值最多。每行所在方位区间、每列所在频率单元上的值对应累加后的最大值输出，单位1.0×107，反映了该区间的空间能量分布。由2.2节特征5，每次的方位输出取谱极大值中的最大值，来由于此。可以发现目标线谱频带所在方位区间的值高于该区间的其他频带，为2.254。宽带强干扰各频带在它所在的方位区间的值都比第1，4行要大。第3行所有频带值累加值大于第2行累加，所以宽带能量积分时，弱线谱目标被淹没。

表3反映了各行所在方位区间、每列所在频率单元上20次统计时，最大空间谱输出的峰均比，可知目标线谱频带fcHz、方位105°～114°区间内的峰均比为61.47，相比该频带其他区间最大；但fc+23 Hz以及未列出频率单元的峰均比大于该频带，注：计算时均值相同。结合表1，2可知，选择频带输出时，选取累加波束输出中超过半功率点中方位方差最小的区间。融合各频带空间谱输出时，保留频带输出中超过各频带空间谱输出最大值一定门限的频带输出，若有不同频带取相同的方位输出时，取这些频带中方位方差最小的。图10是取10次连续统计的结果，本文方法可以有效的检测到弱线谱目标。

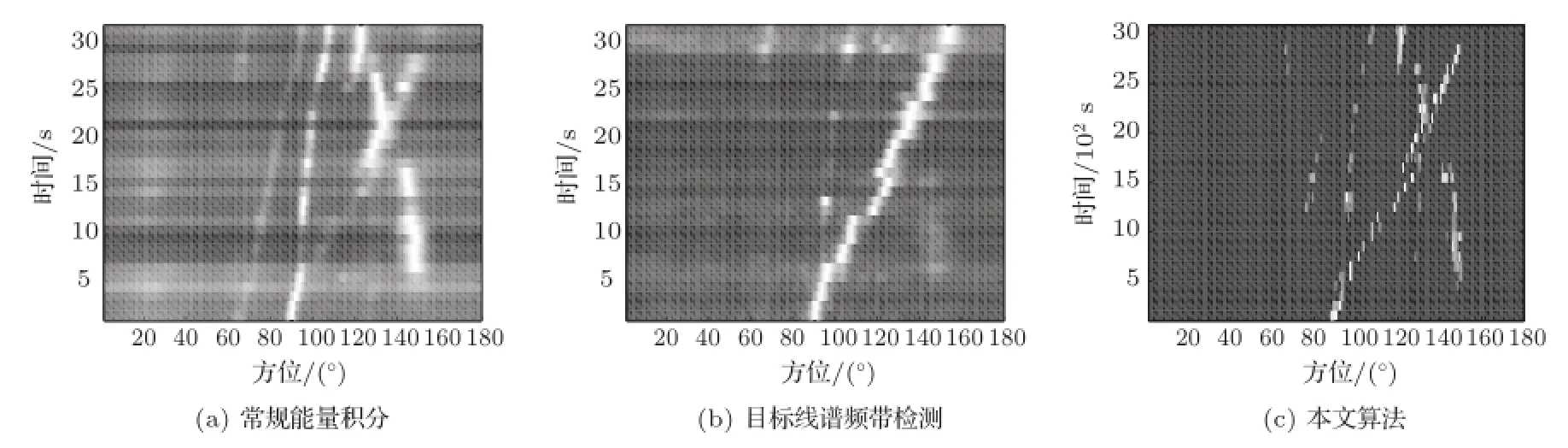
图10　海试实验数据处理的检测结果Fig.10 Contrast of sea trail data processing results

6　结论

本文从线列阵频域波束形成子带分解频带统计特性和实验分析结果出发，提出子带分解和分方位区间融合算法，获得以下初步结论：

（1）当线谱相对谱级足够大，得以稳定检测目标时，分方位区间统计方位方差比整个区间统计方位方差能更多利用辐射噪声线谱的信息；

（2）相干干扰的存在会使常规方位稳定性算法的目标频带方位统计方差变差，而分方位区间统计融合的算法，线谱目标所在区间内统计的方位仍然有很大的精确性；

（3）宽带强干扰的存在同样会使常规方位稳定性算法的目标频带方位统计方差变差，分方位区间统计融合的算法，仍能有效利用目标线谱大而稳定的特性；

（4）当目标线谱频带未知时，为了利用最大输入信噪比检测信号，传统方法需要对分析频带内每个频率单元的波束输出结果循环判断才能实现目标的正确检测，本文提出的方法则不需要。

子带分解和分方位区间融合方法，检测效果好，结果输出直观、简便，适合工程使用。

［1］侯自强.声纳信号处理—原理和设备［M］.北京：海洋出版社，1983：32-33.

［2］李启虎.声纳信号处理引论［M］.北京：海洋出版社，2000：120-123.

［3］蒋国健，林建恒，马杰，等.舰船螺旋桨空泡噪声的数理模型［J］.声学学报，1998，23（5）：401-408.

JIANG Guojian，LIN Jianheng，MA Jie，et.al.Theoretical model of noise caused by ship propeller cavitation［J］. Acta Acustica，1998，23（5）：401-408.

［4］吴国清，王美刚，陈耀明.水声波导中包络线谱强度数值预报［J］.声学学报，2012，37（4）：432-439.

WU Guoqing，WANG Meigang，CHEN Yaoming.Numerical prediction of envelope line spectrum intensity in underwater acoustic waveguide［J］.Acta Acustica，2012，37（4）：432-439.

［5］吴国清.周期性局部平稳过程双重谱图分析和测量［J］.声学学报，1980，（2）：100-109.

WU Guoqing.Analysis and measurement of double frequency spectra of periodically locally stationary radom process［J］.Acta Acustica，1980，（2）：100-109.

［6］COETZER M W，LOURENS J G.Signal processing techniques to analyze and simulate radiated underwater ship noise［M］.Proc.of NATO ASI on Underwater，（D.Reidel Publishing Co.），Boston，1984.

［7］吴国清.背景噪声中检测舰船辐射噪声的周期调制的性能估算［J］.声学学报，1982，7（4）：222-232.

WU Guoqing.Performance prediction about detection of periodical modulations of ship noise in background noise［J］.Acta Acustica，1982，7（4）：222-232.

［8］WILLIS W H.Principle of the statistical theory of communication［M］.New York：McGraw-Hill，1963：194-206.

［9］吴国清，魏学环，周刚.提取螺旋桨识别特征的二种途径［J］.声学学报，1993，18（3）：210-216.

WU Guoqing，WEI Xuehuan，ZHOU Gang.Two ways of propeller recognition feature extraction［J］.Acta Acustica，1993，18（3）：210-216.

［10］陈新华，鲍习中，李启虎.水下声信号未知频率的目标检测方法研究［J］.兵工学报，2012，33（4）：471-475.

CHEN Xinhua，BAO Xizhong，LI Qihu.Research on detection of underwater acoustic signal with unknown frequency［J］.Acta Armamentarii，2012，33（4）：471-475.

［11］陈新华，余华兵，孙长瑜.一种水声目标信号检测和识别方法：中国，101738611A［P］.2012-08-15.

［12］陈阳，王自娟，朱代柱.一种基于频率方差加权的线谱目标检测方法［J］.声学学报，2010，35（1）：76-80.

CHEN Yang，WANG Zijuan，ZHU Daizhu.A detecting method for line-spectrum target based on variance-of-frequency weight［J］.Acta Acustica，2010，35（1）：76-80.

［13］郑恩明，陈新华，孙长瑜.基于频率方差加权的时延差估计方法［J］.系统工程和电子技术，2014，36（2）：224-229.

ZHENG Enming，CHEN Xinhua，SUN Changyu.Time delay difference estimation weighted method based on frequency variance［J］.System Engineering and Electronics，2014，36（2）：224-229.

A fusion algorithm for passive detection of the line spectrum target based on the sub frequency and sub interval statistics

DAI Wenshu1，2CHEN Xinhua1SUN Changyu1
（1 Institute of Acoustics，Chinese Academy of Sciences，Beijing 100190，China）
（2 University of Chinese Academy of Sciences，Beijing 100049，China）

As we all know，the target underwater radiates abundant low frequency line elements with not only high spectrum level but also intensive stability.The existing methods based on sub frequency band processing are appropriate for the situation where the signal to noise（SNR）ratio is high enough.While the coherent or wide band interferences exist，effective detection of the target of line-spectrum is not yet having a good solution.This article studies the characteristics of spatial spectrum after frequency domain beam forming and makes full use of characteristic that a line spectrum is 10～25 dB higher than that of the continuous spectrum level.Since the output azimuth of the subinterval where the target lies has a smaller fluctuation than the other subintervals，we propose an effective fusion algorithm which applies in a situation with lower SNR as well as the coexistence of multi-objective.The innovation and the effectiveness have been demonstrated by the simulation and the sea trial data processing results and this method can be more wildly used than the conventional azimuth stability algorithm.It's very much suitable for engineering applications.

Low frequency line spectrum detection，Information fusion，Sub frequency，Sub interval signal processing

TB561

A

1000-310X（2015）03-0227-09

10.11684/j.issn.1000-310X.2015.03.007

2014-06-04收稿；2014-08-26定稿

∗国家自然科学基金面上项目资助（61372180）

戴文舒（1987-），女，山西祁县人，博士研究生，研究方向：水声信号低频线谱检测。†

E-mail：dws.01@163.com