基于数字地面模型的立式金属罐底量测量方法研究

王龙龙， 侯松梁， 黄朝晖， 刘子勇， 佟 林， 暴雪松

（1.江苏省计量科学研究院，江苏 南京 210007； 2.中国计量科学研究院，北京 100029）

基于数字地面模型的
立式金属罐底量测量方法研究

王龙龙1， 侯松梁1， 黄朝晖1， 刘子勇2， 佟 林2， 暴雪松2

（1.江苏省计量科学研究院，江苏 南京 210007； 2.中国计量科学研究院，北京 100029）

针对如何准确测量出发生不规则变形的立式金属罐底量，提出一种基于数字地面模型的测量方法，该方法通过解算由罐底三维坐标点构建的不规则三角网所对应体积而求出罐底量。所构建不规则三角网能够以等高线形式完整表达罐底的起伏特征，为后期罐底变形研究提供参考。实验中以容量比较法为标准，对几何测量法和数字地面模型测量法进行对比实验研究，结果表明该方法适用于立式金属罐的底量测量，相对误差较几何测量法平均降低了2.5%。

计量学；立式金属罐；底量；几何测量法；数字地面模型；不规则三角网；全站仪

1　引 言

立式金属罐是油品、化工品贸易交接和仓储计量的主要计量器具，其结果的准确程度直接影响企业的经济效益。在立式金属罐的检定项目中，底量是其计量不确定度的主要来源之一。检定规程要求优先采用容量比较法测量底量，该方法测量准确度高，但实际中因财力、物力、人员、时间等方面的消耗过大而难以施行。几何测量法适用于规则对称且没有发生变形的罐底测量，国际建议OIML R71：2008对此亦有明确说明［1～5］。

针对如何准确测量形状不规则对称或已发生不规则变形的罐底，提出一种基于数字地面模型（Digital Terrain Model，简称DTM）的立式金属罐底量测量方法。该方法根据被测罐底的起伏特征，对罐底的特征位置进行逐点测量，通过解算罐底三维坐标点所构建的不规则三角网实现对形状不规则对称或已发生不规则变形的罐底底量测量［6～10］。

2　几何测量法与DTM底量测量法

几何测量法是解算同心等面积圆环对应体积的过程，DTM底量测量法在解算三角网的基础上计算罐底量，它在三角网的基础上解决了不规则变形罐底难以准确测量的问题。

2.1几何测量法

几何测量法原理是将罐底分成m个同心等面积圆环和n条均匀分布的半径线，如图1所示，用水准仪读取各个交点以及中心点与基准点的高程坐标，通过计算各圆环对应体积求得罐底量。

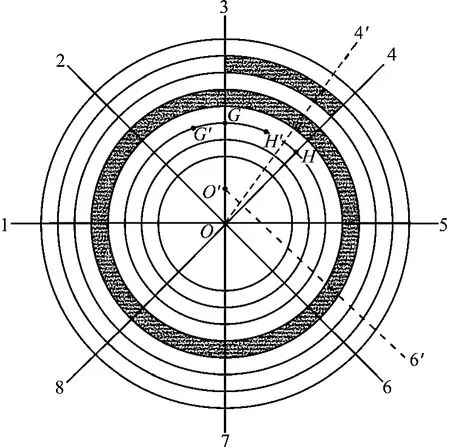
图1　测量点分布示意图

几何测量法在点位布置上具有一定的局限性，测量点位相对确定，不能完整的表达罐底的起伏特征。图1中H点、H′点、G点、G′点4点处的起伏较大，依据规程要求，测量H点和G点的同时不能对H′点和G′点进行测量，即不能同时对4点进行测量。可见几何测量法在点位布置上具有一定的局限性。几何测量法中的实际测量位置易偏离理论预期位置。如图1所示，O4线和O6线为理论预期位置，因罐内结构复杂或其他因素导致实际测量的位置为O4′线和O′6′线。这种因罐内结构复杂而造成的情况往往很难避免，同时规程中也缺乏相关情况的说明，导致结果误差偏大。

2.2DTM底量测量法

DTM底量测量原理：测取一系列能表达罐底起伏特征的坐标点（特征点），将坐标点连接成连续且互不重叠的三角形，组成不规则三角网，如图2、图3所示，将三角网向基准点对应的水平面投影，投影网与三角网之间的体积加上边缘弧形对应的体积即为罐底死量，扣除罐底最高点与基准点之间的体积即为罐底量。式中SA′B′C′为△A′B′C′的面积。则三角网与基准点对应水平面之间的体积V△为：

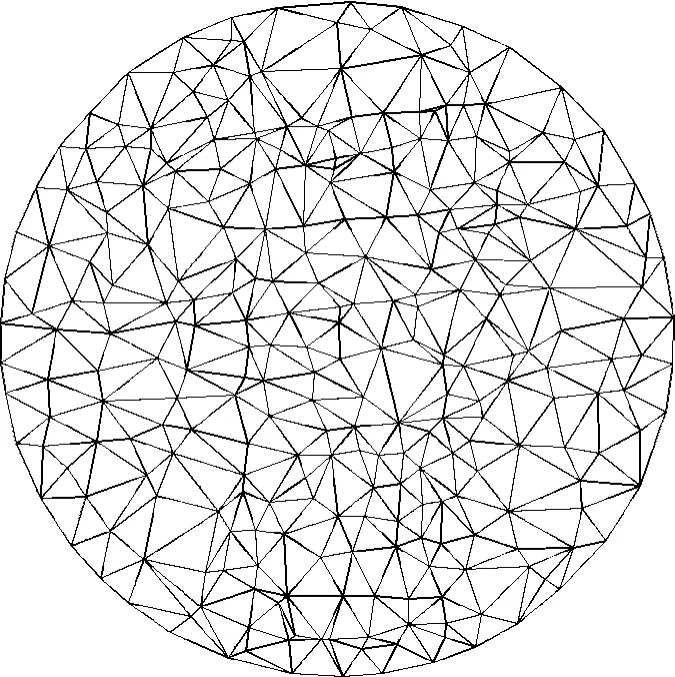
图2　不规则三角网示意图

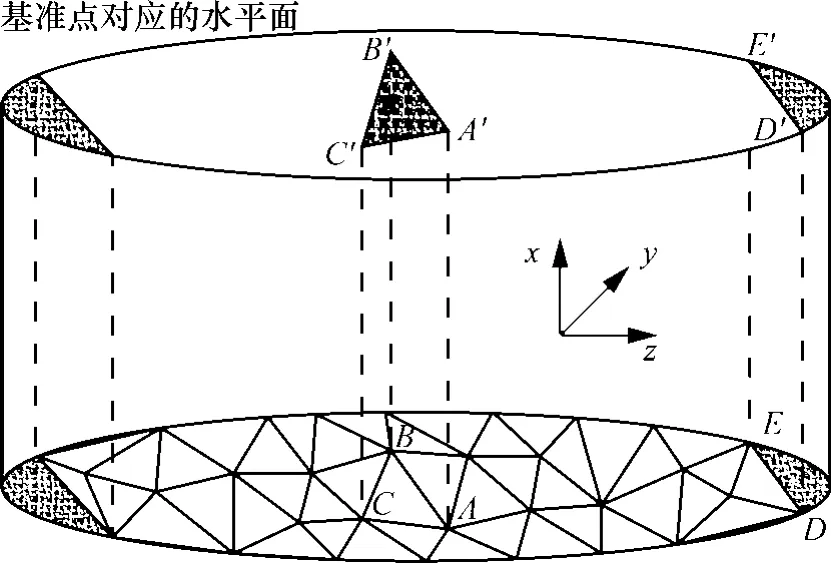
图3　三角网投影示意图

式中R为罐底直径。则图3中边缘弧形Y与基准点之间的的体积VY为：

3　对比实验及数据分析

对DTM底量测量法进行现场实验验证，并与几何测量法、容量比较法进行对比实验研究，分析结果，判断其准确性与适用性。

3.1对比实验系统

实验以H-20204-050、V-202、TA-204三个罐底发生不规则变形，标称容量为5000 m3的立式金属罐为研究对象，进行DTM底量测量法、容量比较法和几何测量法的对比实验研究。实验步骤如下：第1步，采用容量比较法和几何测量法分别进行测量，具体操作要求参照JJG 168-2005规程；第2步，采用DTM底量测量法进行测量，先测基准点，后取边缘点，最后特征点。基准点可重复测量多次，必要时记录在原始记录上。边缘点测取时注意闭合，见图2。特征点测量方式可参照SH 3046-1992［11］中的底板排列方式进行逐一测量。为保证测量精度，对直径超过6 m的立式金属罐，采取棱镜测量，从而减小入射角，提高测距精度［12］。DTM底量测量系统属于半自动测量系统。采用人工判别点位的方式获取特征点，主要是为避免自动扫描时因罐内结构复杂而难以判别所造成的数据失准。测量数据全部使用软件进行处理，整体工作效率较高。

3.2实验数据分析

根据上述要求对H-20204-050、V-202、TA-204进行测量，测量结果见表1、表2、表3，其中相对偏差为各方法相对容量比较法的偏差。

表1　H-20204-050测量结果

表2　V-202测量结果

表3　TA-204测量结果

由表1～表3中数据可知，测得H-20204-050、V-202、TA-204的相对偏差较几何测量法分别提高2.2%、1.8%、3.4%，平均提高2.5%，说明DTM底量测量法优于几何测量法。

采用DTM底量测量法进行测量时，罐底的特征点数量见表4。其中，V-202特征点最稀疏，相对偏差最大，TA-204特征点最密集，相对偏差最小。说明使用DTM底量测量法进行测量时，单位面积的特征点越多，该方法越逼近容量比较法，相应结果的准确度也越高。

表4　特征点数量

H-20204-050、V-202、TA-204采用DTM底量测量法进行测量时，底量部分引入整体的不确定度分别是7.11×10-5、2.72×10-4、4.28×10-5。置信概率为95%，包含因子为2时，H-20204-050、V-202、TA-204的总不确定度分别为0.062%、0.082%、0.061%，均小于0.1%，满足立式金属罐的计量要求。

对罐底数据进行可视化处理。通过数学建模，利用等高线表达罐底起伏特征实现数据可视化，使其能明确有效地传递罐底信息，加深对罐底数据的认识与理解。理论上，规则倾斜罐底的等高线是一系列均匀分布的弧线，实际中，立式金属罐罐底在罐料压力的作用下会随着时间的推移而发生不规则变形。如图4中的等高线表明TA-204罐是一发生了不规则变形的倾斜罐底，其等高线突变的位置即是罐底发生变形的位置。数据可视化实现了罐底形态的直观表达，对罐底变形预测与变形研究具有重要指示作用。

图4　TA-204罐底等高线示意图

4　结 论

（1）针对如何准确测量形状不规则或已发生不规则变形的立式金属罐罐底，提出一种基于数字地面模型的立式金属罐底量测量方法，该方法解决了几何测量法中点位布置受限和测点易偏离理论预期位置的问题。（2）对比实验表明，以容量比较法为参考依据，DTM底量测量法测得底量的相对偏差明显小于几何测量法，其测量准确度随着特征点密度的增加而提高，满足不确定度小于0.1%（k=2）的计量要求，验证了这种方法的有效性。（3）DTM底量测量法实现了罐底形态的可视化表达，对罐底的变形预测与变形研究具有重要指示作用。

［1］ 国家质量监督检验检疫总局.JJG 168-2005立式金属罐容量［S］.

［2］ OIML R712008，Fixedstoragetanks，General requirements［S］.

［3］ 刘子勇.容量计量［M］.北京：中国计量出版社，2009.

［4］ Nosach V V，Belyaev B M.The Calibration of Large Vertical Cylindrical Tanks by a Geometrical Method［J］. Measurement Techniques，2002，45（11）：1153-1157.

［5］ Richard M S.Calibrationofstoragetanks［C］// Proceedings of the Internation School of Hydrocarbon Measurement，Ohio，USA，1985：428-432.

［6］ 王金涛，刘子勇，佟林，等.基于点云分析的大型立式液态石化产品储罐容量计量方法研究［J］.计量学报，2011，32（2）：110-113.

［7］ 佟林，王金涛，刘子勇，等.基于光电内测法的立式罐容量计量中圈板半径拟合算法的研究［J］.计量学报，2011，32（6）：522-525.

［8］ 刘焕桥.立式金属罐的底量计量问题［J］.油气储运，1988，7（6）：56-59.

［9］ 慕永峰，朱昌勇，李建.三角网结构DTM的土方计算及应用［J］.测绘工程，2000，9（1）：52-56.

［10］ 柯正谊，何建邦，池天河.数字地面模型［M］.北京：中国科学技术出版社，1993.

［11］ 中国石油化工总公司.SH 3046-1992石油化工历史圆筒形钢制焊接储罐设计规范［S］.1992.

［12］ 夏立福，李井春，胡友健，等.免棱镜全站仪测距性能的测试及精度分析［J］.地理空间信息，2008，6（2）：133-135.

Research on the Volume Measurement Method of the Vertical Metal Tank Bottom Based on Digital Terrain Model

WANG Long-long1， HOU Song-liang1， HUANG Zhao-hui1，LIU Zi-yong2， TONG Lin2， BAO Xue-song2
（1.Jiangsu Institute of Metrology，Nanjing，Jiangsu 210007，China；2.National Institute of Metrology，Beijing 100029，China）

In order to accurately measure the irregular deformation for the bottom of the vertical metal tank，a method based on digital terrain model was proposed.The bottom was calculated by the capacity of the triangulated irregular network which was built by three dimensional coordinates.This method will provide useful guidelines for future studies of the bottom deformation under the contour line expressed the undulations of the bottom completely.With a standard of the volumetric method，there is a comparison between the geometric method and the digital terrain model method in this experiment.The experiment results showed that the method is applicable to the bottom measurement of the vertical metal tank.Compared with the geometric method，the relative error was reduced 2.5%averagely.

metrology；vertical metal tank；bottom；geometric method；digital terrain model；triangulated irregular network；electronic total station

TB938.3

A

1000-1158（2015）05-0487-04

10.3969/j.issn.1000-1158.2015.05.09

2014-07-21；

2015-01-15

国家自然科学基金（51105347，51475440）

王龙龙（1989-），男，内蒙古乌兰察布人，江苏省计量科学研究院助理工程师，主要从事容量计量科学技术的研究。489480915@qq.com