一种圆鞍形磁屏蔽线圈的设计与性能研究

赵伟霞， 董全林， 孙茂多， 丁 莹， 杨娅姣， 党玉杰

（北京航空航天大学仪器科学与光电工程学院，北京 100191）

一种圆鞍形磁屏蔽线圈的设计与性能研究

赵伟霞， 董全林， 孙茂多， 丁 莹， 杨娅姣， 党玉杰

（北京航空航天大学仪器科学与光电工程学院，北京 100191）

以毕奥-萨伐尔定律为基础，推导了一种圆鞍形线圈在空间任意点处的磁场分布表达式，优化了一种线圈结构，证明了圆鞍形线圈可以产生一定区域的稳恒磁场，并定量地给出了线圈内部磁场的空间分布情况。所设计线圈产生的磁场中，1%均匀度的磁场均匀区占轴上区域的28%，0.1%均匀度的磁场均匀区占轴上区域的10%；在1 mA的电流下，单圈线圈最大磁场补偿值为15 nT，相对偏差量不超过0.14 nT，验证了所推导表达式的正确性，为多维磁场补偿系统设计与研究提供了理论依据和参考。

计量学；稳恒磁场；毕奥-萨伐尔定律；圆鞍形线圈；磁屏蔽

1　引 言

在原子陀螺、电子显微镜、超冷原子团温度和密度测量、超高灵敏度磁强计等许多精密测量领域中，地磁场、杂散磁场等环境磁场会引起测量误差［1～3］，因此需要进行补偿和屏蔽。目前广泛采用的是磁场产生系统，它利用3组轴心线互相垂直的线圈组，通以适当的稳恒电流，沿3个不同方向产生可控稳恒磁场与外部磁场矢量叠加抵消，使预定区域达到零磁场（磁场强度微弱）的效果，从而屏蔽环境磁场的影响［4］。

磁场产生系统的主体是产生磁场的线圈，用来描述线圈的指标有线圈常数和磁场均匀度［5］。线圈常数是指线圈中心产生的磁场强度与通入的电流强度之比，反映了线圈产生磁场的能力；磁场均匀度是指一定半径球面上的磁场与圆心处磁场的相对变化量，反映了线圈磁场的均匀性。可产生均匀磁场的线圈有螺线管形、方形、环形、矩鞍形等线圈。传统的螺线管线、方形、环形线圈结构庞大，不易安装，而鞍形线圈相较其他线圈可使系统结构简化、体积减小、安装方便、耗能降低，非常适用于原子陀螺、原子钟等需要微小结构的磁屏蔽系统。另外由于矩鞍形线圈特有的异型形状切合圆柱形人体，因此在无线内窥镜、核磁共振成像等医疗领域得到应用［6～8］。

由于矩鞍形线圈存在不易绕制、拐角处易偏移和漆包线涂层破损等情况，本文考虑了不存在直形拐角的圆鞍形线圈，研究其内部任意点处的磁场变化情况，并进行仿真验证，避免直形拐角存在，提高磁场精度，为其在原子陀螺、电子显微镜等领域的应用开辟一条新的设计方法。

2　圆鞍形载流线圈的空间磁场分析

2.1圆鞍形载流线圈空间磁场理论计算

圆鞍形是圆形紧贴柱面上弯曲后形成的马鞍形状，如图1所示。以对称放置的圆鞍形载流线圈S1、S2的中心为原点建立空间直角坐标系O-xyz，穿过线圈圆心O1、O2的方向为x轴，向右垂直O1O2的方向为y轴，z轴垂直于xOy平面。

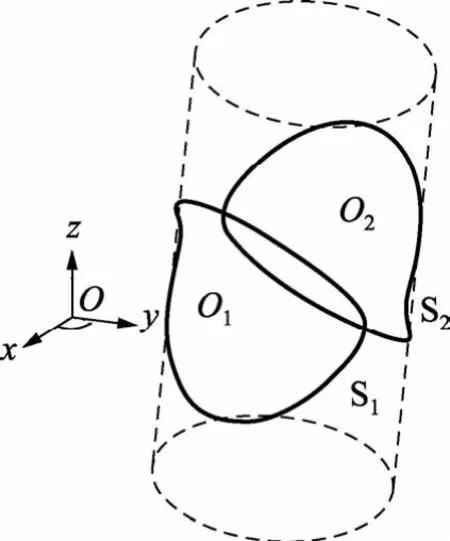
图1　圆鞍形载流线圈坐标图

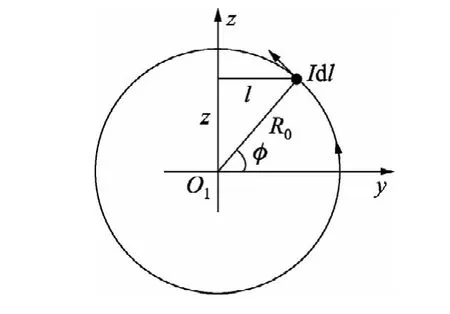
图2　未弯曲前的线圈形状

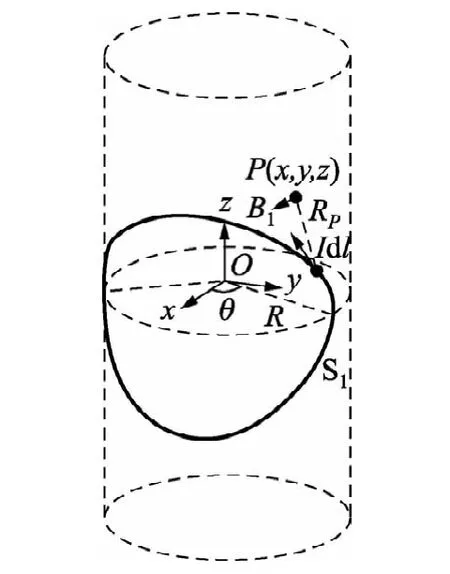
图3　线圈电流元在场点处磁场分布示意图

式中，μ0为真空磁导率，单位是H·m-1；R为电流元到场点的距离，单位是m；I为线圈电流，单位是A；B为磁感应强度，单位是T。

由式（1）～（3）可得单侧线圈S1在空间任意一点产生的x、y、z三个方向的磁场强度为：

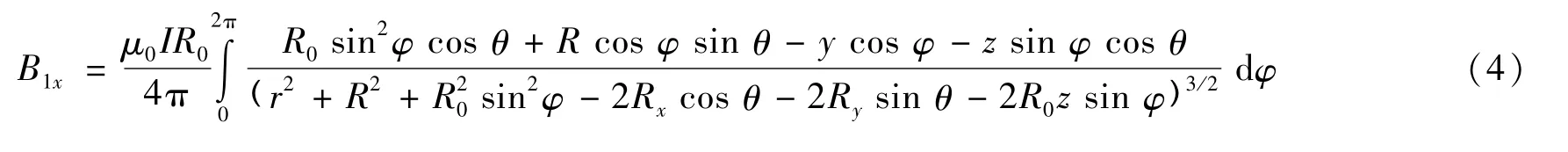
同理可求得中心线放置在x轴负半轴的圆鞍形线圈S2产生的空间磁场强度。单侧线圈S2在空间任意一点各方向产生的磁场强度为：

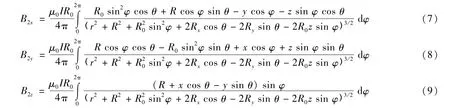
式（4）～式（9）中，μ0为真空磁导率，I为线圈通入的电流，R0为弯曲前圆形线圈的半径，R为弯曲后圆鞍形线圈柱体的半径，r2=x2+y2+z2，θ=R0cos φ/R。

通过以上分析，一组对称放置的圆鞍形线圈S1和S2叠加作用在空间任意场点产生的x、y、z三个方向的磁场强度为：

S1和S2在空间任意场点产生的总磁场强度为：

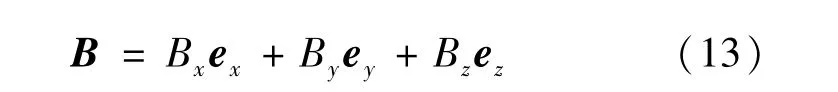
同理，两个对称放置的圆鞍形载流线圈中心线位于y轴时，可以得到与式（10）～式（13）相似的表达式。

2.2圆鞍形载流线圈轴上磁场理论计算

为进一步了解圆鞍形线圈内部磁场分布情况，对圆鞍形系统进行轴上磁场分布分析。当场点P位于x轴时，即令式（4）～式（9）中的y、z为0，得圆鞍形线圈组S1和S2产生的x、y、z三个方向的磁场强度为：

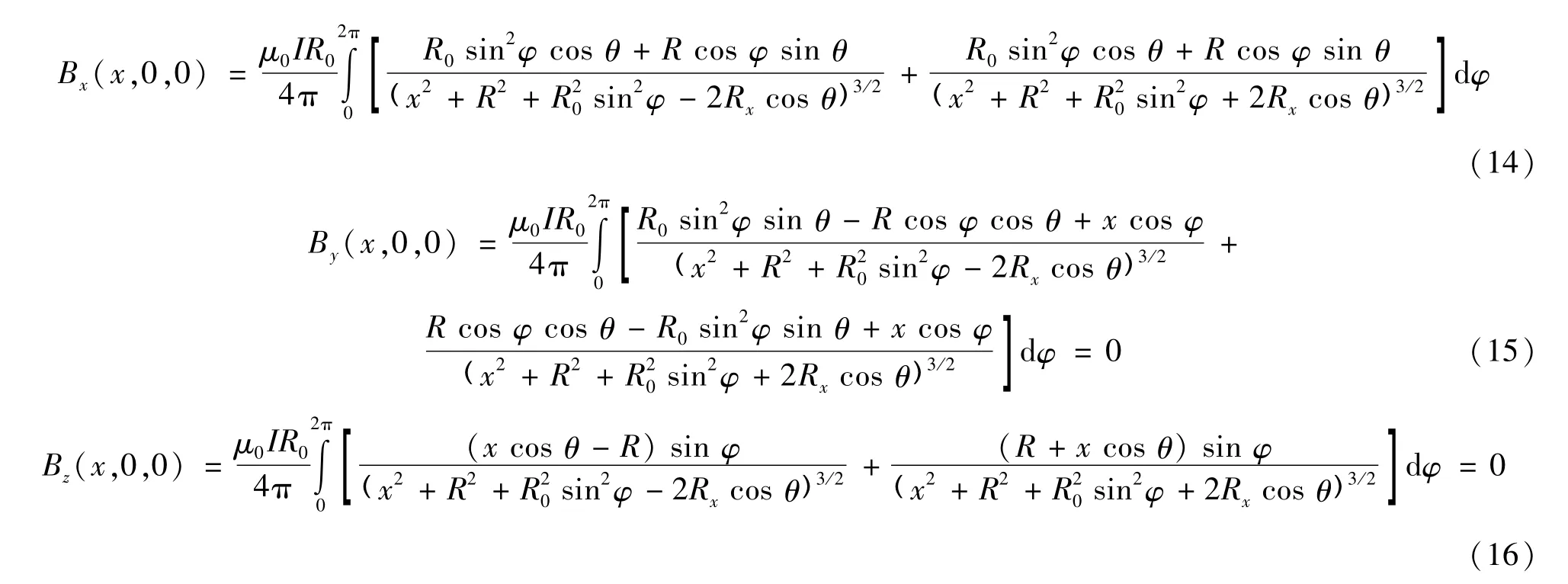
可见，在x轴上y、z两个方向的磁场强度为0，线圈只产生x方向的磁场强度，这为线圈的分析和利用打下了基础。同理可以求出，当场点P位于y、z轴时，线圈在该点处也只产生x方向的磁场强度。

通过上面分析，x轴放置的圆鞍形线圈在轴上只产生x方向的磁场，其它方向的磁场强度为0。这样，可以通过把几组线圈放置在不同轴上来对相应轴向磁场进行独立补偿，彼此间不受影响。

2.3圆鞍形线圈产生均匀磁场的条件

由上面的分析可知x轴上放置的圆鞍形线圈在轴上产生的磁场为B（x）=Bx（x，0，0），将其在x=0处泰勒展开为：

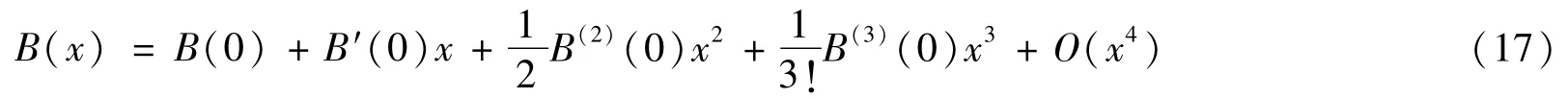
由于B（x）为偶函数，故奇次项导数B′（x）=0、B（3）（0）=0，…，B（2n+1）（0）=0，而当x的值很小时（0＜x＜1），O（x4）≈0，可以忽略它对磁场的影响。若使得圆鞍形线圈在中心附近产生均匀的磁场，要满足的条件为：

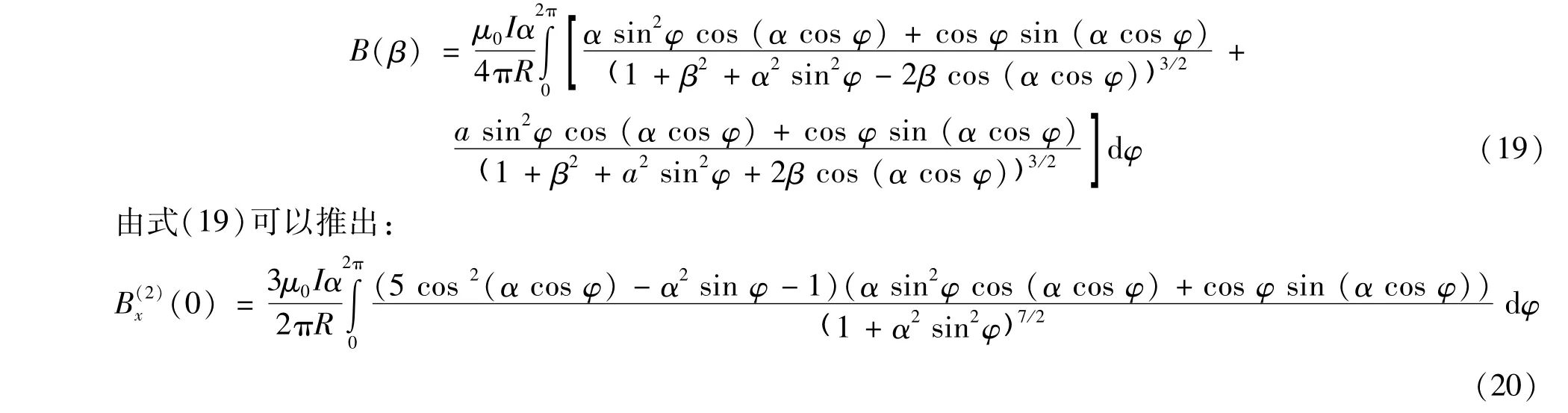
式（20）不存在解析解，因此利用逐步逼近法由式（18）、式（20）计算得出数值解α=2.119 5，即圆鞍形线圈产生均匀磁场的条件为R0=2.1195 R，其中R0为线圈半径，R为柱体半径。

3　圆鞍形载流线圈磁场仿真结果

由上面的分析可以确定，圆鞍形线圈弯曲程度即柱体半径决定了其均匀磁场的范围。对线圈性能进行定量分析，取I=1 mA，R=50 mm，R0=105.975 mm，对模型进行Matlab仿真。圆鞍形线圈在3个坐标轴上产生的磁场强度分布曲线和磁场均匀性分别如图4（a）、图4（b）所示。

为更准确地展示圆鞍形线圈产生的磁场强度情况，表1给出了线圈在x轴上不同点处产生的磁场强度值和磁场偏差量。

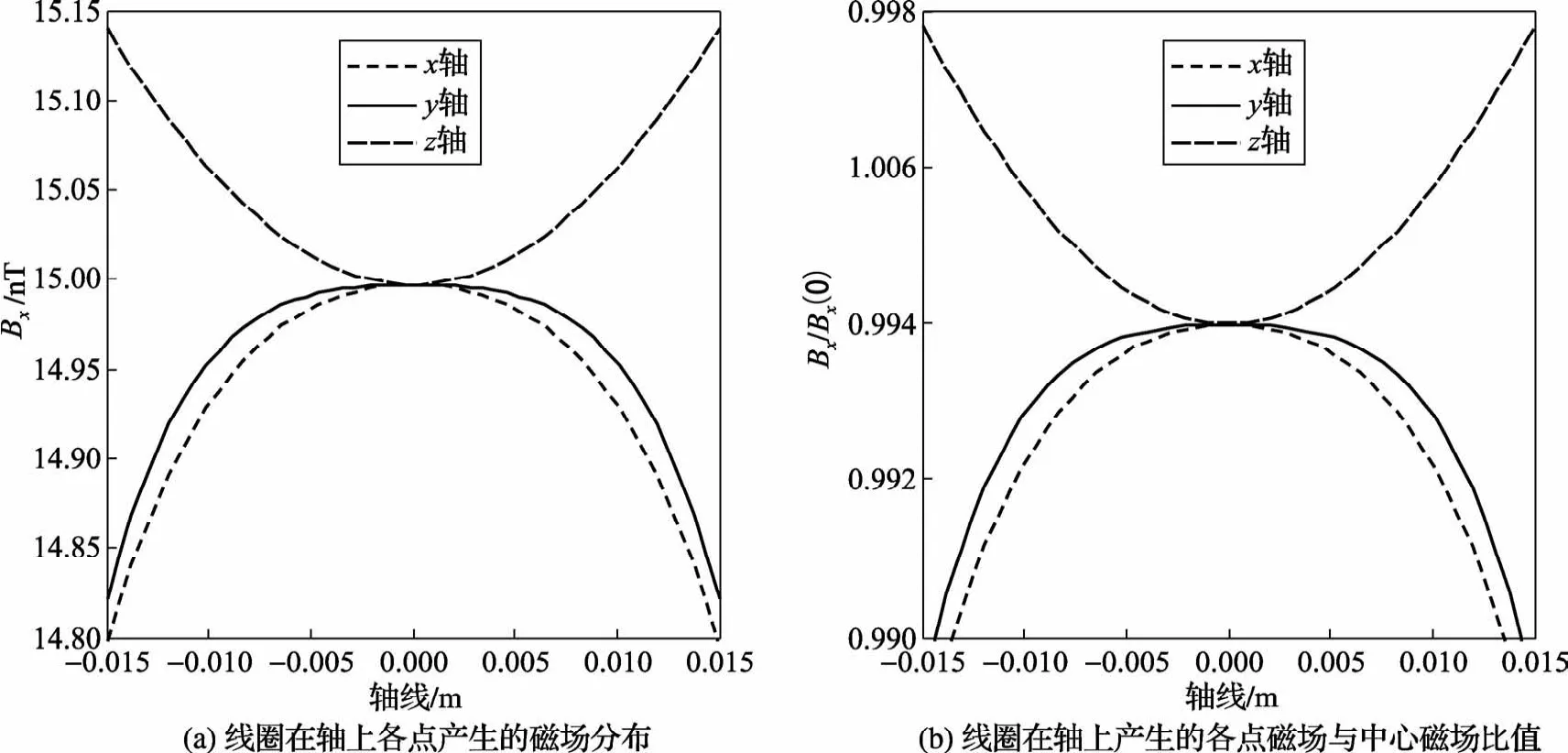
图4　圆鞍形线圈轴上磁场分布情况

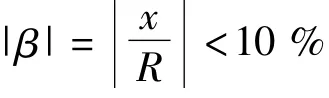
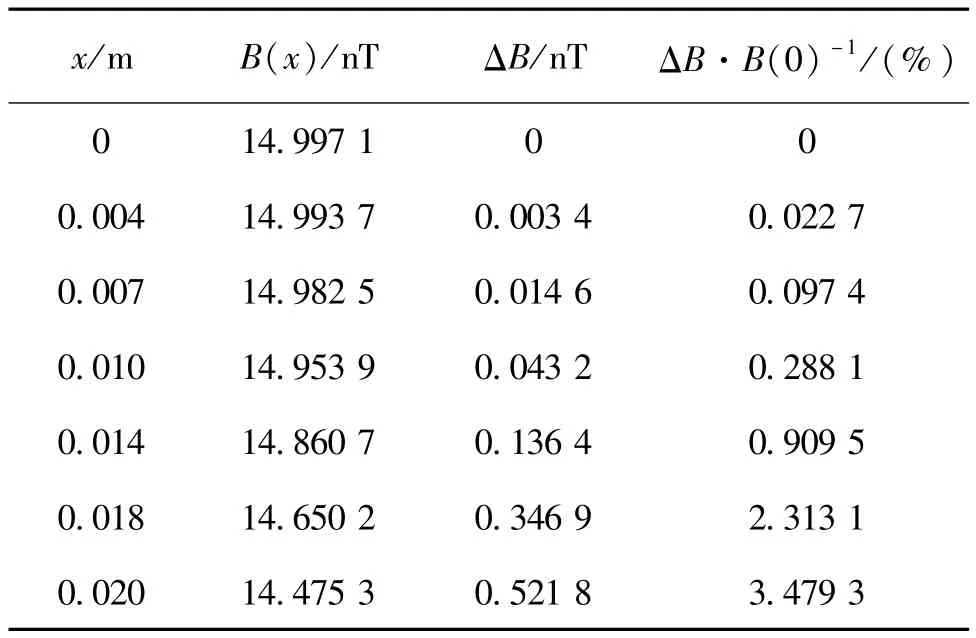
表1　线圈在x轴上产生的磁场强度和磁场偏差量

为进一步分析线圈内部磁场分布，对圆鞍形线圈在xOy平面上产生的x、y、z三个方向的磁场分布进行分析，仿真结果如图5、图6、图7所示。

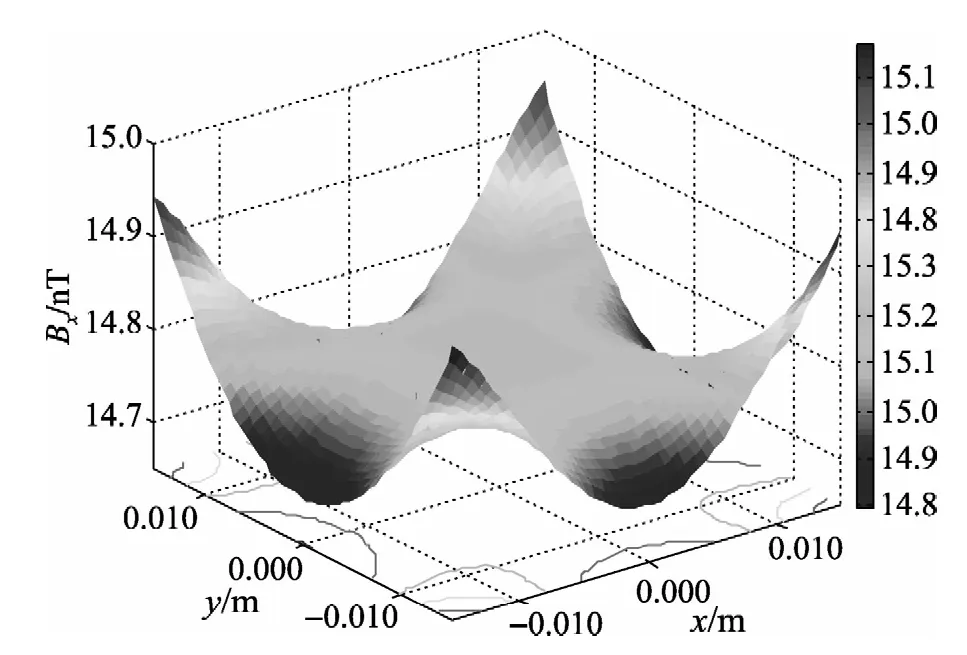
图5　xOy平面上x方向磁场强度和等值线分布

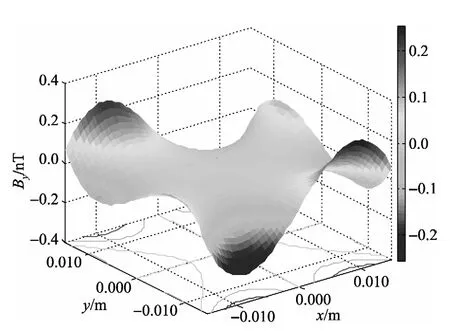
图6　xOy平面上y方向磁场强度和等值线分布

可以看出，圆鞍形线圈在xOy平面上产生的y方向磁场分量最大只能达到0.2 nT，而在z方向产生的磁场分量在10-15量级，因此可以认为线圈在xOy平面上只产生x方向的磁场，并且由图5可以看出，线圈在xOy平面上圆心O周围14 mm的圆形区域内能产生不超过15 nT的磁场，均匀性能达到1%，而且与轴上磁场分布情况相同，越靠近中心，其均匀性越好，验证了模型磁场解析表达式的正确性。

为更形象直观地表示圆鞍形线圈空间的磁场分布，选取线圈内30 mm×30 mm×30 mm的空间立体区域，共8 000个采样点进行分析，标记能产生磁场强度在14.997 1±0.15 nT范围内的点，仿真结果如图8所示。

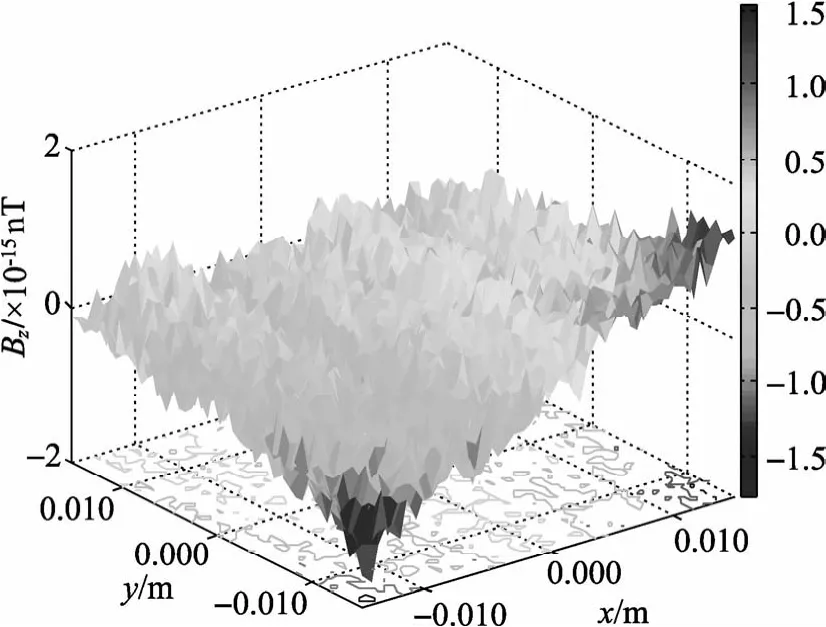
图7　xOy平面上z方向磁场强度和等值线分布

图8　圆鞍形线圈在空间立方区域内的磁场分布

由图8可以看出所标记的点集中分布在线圈中心28 mm×28 mm×28 mm大小的立体空间内，形成一个稳恒磁场区域，表明这种圆鞍形线圈可以在一定空间区域产生稳恒磁场，在磁补偿和屏蔽系统中具有可应用性。

4　结 论

（1）推导了一种圆鞍形线圈在空间任意点处的磁场分布表达式，优化了一种线圈结构，利用Matlab软件画出了线圈的轴上和空间磁场分布图，定量地给出了圆鞍形线圈内部磁场的空间分布情况。

（2）设计的线圈轴向磁场1%均匀度的均匀区为轴上区域的28%，0.1%均匀度的均匀区为轴上区域的10%，验证了所推导表达式的正确性，为多维磁场补偿系统提供了理论依据和参考值。

（3）圆鞍形线圈形成稳定磁场区域的原因是选取了一种结构使得式（17）中B（2）（0）为零，如果要进一步提高磁场的均匀性和均匀区域，可以通过改进使式（17）中B（x）在原点的更高阶导数B（4）（0）、B（6）（0）也为零，可以大大提高屏蔽线圈的性能。

［1］ 赵永明，徐云飞，吴艳，等.通过补偿法获得零磁场环境［J］.浙江大学学报（理学版），2006，（01）：44-47.

［2］ 武海澄，刘正敏，周荷琴.磁共振成像系统中低阶平板式匀场线圈的设计［J］.中国电机工程学报，2005，（24）：154-159.

［3］ 董全林，刘雪萍，张春熹，等.双圈共轴线圈产生错位对激励磁场的影响［J］.计量学报，2013，34（6）：573-578.

［4］ 陆小松，陈群峰，史保森，等.基于冷原子系综制备非经典关联光子对［C］//中国物理学会原子与分子物理专业委员会.第十五届全国原子与分子物理学术会议论文摘要集，贵阳：2009.

［5］ 张伟.高均匀度磁场线圈的设计［J］.计量学报，2010，31（5）：404-407.

［6］ Jeon Seungmun，Jang Gunhee，Choi Hyunchul，et al. Magnetic Navigation System With Gradient and Uniform Saddle Coils for the Wireless Manipulation of Micro-Robots in HumanBloodVessels［J］.Magnetics，IEEE Transactions on，2010，46（6）：1943-1946.

［7］ 李国丽，李剑平，王群京，等.外磁场驱动的无线内窥镜磁场线圈的设计方法研究［J］.中国科学技术大学学报，2008，（03）：272-276.

［8］ Wang X Z，Hao J C，Yu Y，et al.The Design of Coil Assembly Producing Uniform Magnetic Field Using in Plasma Propulsion System［C］//Vacuum Nanoelectronics Conference，2006andthe50thInternationalField Emission Symposium，IVNC/IFES.Technical Digest.19th International，Guilin：2006，379-380.

The Design and Research on Performance of Round-saddle Coils for Magnetic Shielding

ZHAO Wei-xia， DONG Quan-lin， SUN Mao-duo， DING Ying， YANG Ya-jiao， DANG Yu-jie
（Departmental of Instrumentation Science and Opto-electronics Engineering，Beihang University，Beijing 100191，China）

The magnetic field distribution expression of one pair of round-saddle coils at any point in space is theoretically inferred based on the Biot-Savart Law，and the structure of the coils is optimized.The fact that the roundsaddle coils can produce uniform magnetic field of a certain region is proved，and the partial magnetic field distribution of round-saddle coils is given quantitatively.The designed coils can produce uniform magnetic field of a certain area which is 28%of the axis area which the uniformity can be 1%，10%of the axis area which the uniformity can be 0.1%.The maximum value of the magnetic field compensation of coils of one single round can be 15 nT in the current of 1 mA，and the relative deviation is less than 0.14 nT.Therefore the correctness of the magnetic field distribution expression is verified，providing the theoretical basis and reference for the design and research of the dimensional magnetic field compensation system.

metrology；uniform magnetic field；biot-savart law；round-saddle coils；magnetic shielding

TB972

A

1000-1158（2015）05-0540-06

10.3969/j.issn.1000-1158.2015.05.20

2014-01-27；

；2015-01-23

国家科技支撑计划（2006BAK03A24）；国家自然科学基金委重大科研仪器设备研制专项（61227902）

赵伟霞（1989-），女，河北临漳人，北京航空航天大学硕士研究生，研究方向为超显微仪器与电子光学技术。zhaoweixia@aspe.buaa.edu.cn

董全林为本文通讯作者。dongquanlin@buaa.edu.cn