基于误差分解定权的工业测量空间线面拟合算法

潘国荣， 郭 巍， 周跃寅

（同济大学测绘与地理信息学院，上海 200092）

基于误差分解定权的工业测量空间线面拟合算法

潘国荣， 郭 巍， 周跃寅

（同济大学测绘与地理信息学院，上海 200092）

针对工业工件拟合中测量数据由于测量仪器特性导致的不同方向误差分量差异问题进行了研究，提出了基于误差分解定权的工业测量拟合算法。该算法考虑了工件姿态以及测量仪器和测点的空间关系，分析了纵向误差和横向误差分量对空间直线和空间平面拟合的影响，然后通过影响量对测量数据进行定权，从而削弱仪器测量误差对拟合结果的影响，提高工件拟合精度。实验结果表明，该算法相比等权拟合精度可提高约16%。

计量学；工件拟合；误差分解；加权拟合；工业测量

1　引 言

工业测量拟合在工业构件制造与检测中广泛应用，快捷的测量方法和高精度的拟合算法成为研究的热点［1，2］。文献［3］基于平差理论研究了新的空间圆球拟合算法，文献［4］和文献［5］分别基于粗差剔除和空间分布特性研究了点云的平面拟合，文献［6］将直线拟合应用于角点检测。全站仪、激光跟踪仪等仪器为较大尺寸工件的测量提供了高效手段，然而由于极坐标测量系统往往具有不同量级的测角精度和测距精度，以及测量仪器相对测点的位置不同，从而导致测点测量数据误差椭圆大小和轴方向的不同。一般工业拟合计算中是将点位误差进行等权处理［7］，未考虑测点误差方向分量的差异性。

本文提出的算法考虑了仪器和测点相对空间关系，以及待拟合工件的形状和姿态，将测量误差分解为纵向误差和横向误差，并依此为参与拟合计算的测点数据定权。

2　误差分量影响分析

2.1相关定义

（1）纵向误差：与目标工件在测点处切平面垂直的误差分向量，记为EV。

（2）横向误差：与目标工件在测点处切平面平行的误差分向量，记为EH。

记测量仪器的测角误差为ζ（在测点处转化为点位误差），测距常数误差为a，测距系数误差为k，记仪器中心位置为P0（X0，Y0，Z0），记某测点测量结果为Pi（Xi，Yi，Zi）（i∈N），测站-测点连线与线、面夹角为αi，测距误差为εdi，测角误差在空间距离上的对应量为εαi。

2.2空间直线与平面测点的误差分解

对于直线和平面来说，等量的纵向误差和横向误差对其拟合精度影响差异如图1所示。

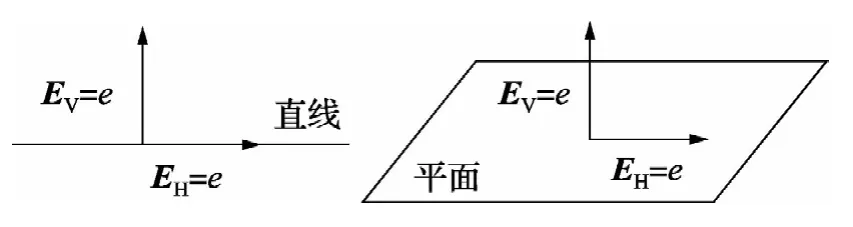
图1　纵向误差与横向误差对直线（平面）拟合的影响

可见，对于直线和平面，横向误差不影响其拟合的空间形状和姿态，纵向误差则完整地影响了空间直线和平面的拟合结果。因此，等量的纵向误差和横向误差e对直线εαi和平面的影响比为0∶e。考虑仪器位置，关于直线和平面εdi测点处的误差分解如图2所示。

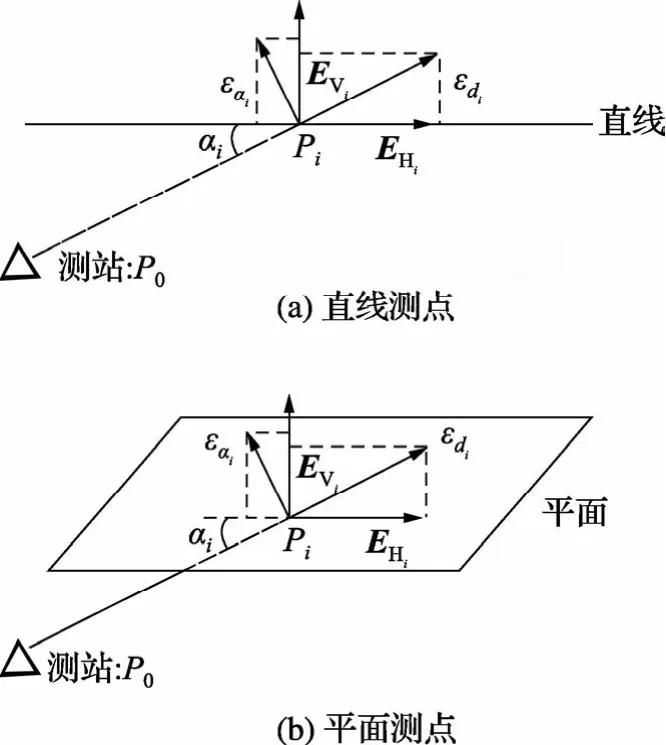
图2　误差分解示意图

下面，考虑测站位置和工件姿态，分析测距、测角精度对线、面上不同位置测点的纵向误差和横向误差的影响，并依此确定定权依据。根据空间几何原理，易得其函数关系为：

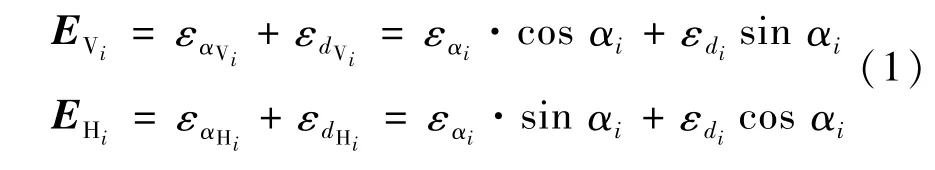
式中，εαi=tan（ζ）·Dis ti，εdi=a+k·Dis ti，Dis ti为测点Pi到测站P0的距离，a为测距常数误差，k为测距系数误差，二者与反射协作目标有关。

由式（1）易知，随着测站—测点连线与直线或平面夹角的增加，纵向误差分量趋向一极值，该极值与测距误差和测量范围有关，而横向误差分量则趋向于零，即当夹角为90度时，只有测角误差存在横向分量，而在小范围内测角误差又非常小。而对于直线和平面，只有纵向误差分量影响其拟合形状和姿态，在此设单位权中误差为1，则其测点拟合定权为：

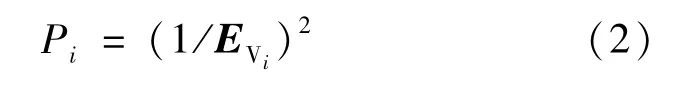
3　误差分解定权拟合算法

误差分解定权拟合算法（Error Decomposition Weighted Fitting Algorithm，简称EDWF）的基本流程为：

（1）先按照各测点等权初步拟合空间线、面，以确定各测站—测点连线以及线、面的空间姿态，为误差分解拟合提供初值，此步引入的姿态误差将在随后的迭代计算中削弱。

然而，在当前的数学教学过程中，很多教师因为数形结合的教学意识不强、疏于对数形结合教学技能的练习，无法在教学过程中准确、规范、清晰、高效的绘制出便于学生理解与记忆的图形。很多教师仍然沿用过去死记硬背、题海战术的教学方法，学生的积极性在复杂繁重又提高不明显的数学学习过程中时常受到打击，教育教学的水平成绩始终得不到长足发展和进步。

（2）考虑仪器测角精度和测距精度，根据第2.2节中提及的误差分解方法，对各测点误差进行分解，提取出影响工件拟合姿态结果的误差分量，并以此分量为各测点再次拟合定权。

（3）依据新权值重新进行不等权拟合计算。

（4）依据（3）中计算出的线、面参数重复执行步骤（2）、（3），直致满足迭代精度要求。

具体算法过程因拟合体的形状不同而不同，下面分别介绍空间直线和空间平面的误差分解定权拟合算法。

3.1空间直线分解定权拟合

空间直线的矩阵形式为：

当待拟合空间直线测量了n个点的三维坐标时，定义矩阵：

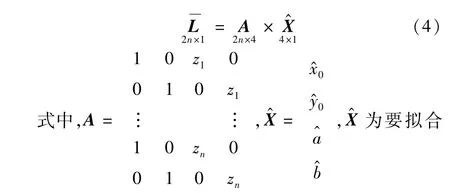
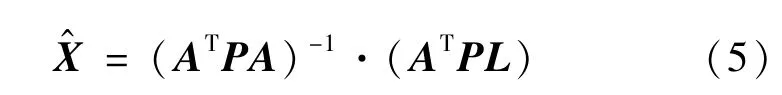
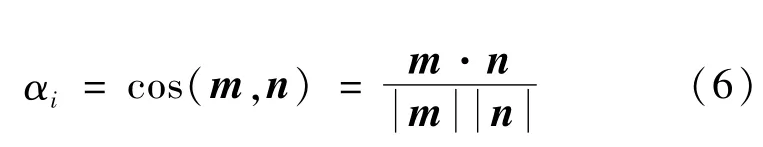
3.2平面误差分解定权拟合

同空间直线拟合类似，当Pi（xiyizi）T（i= 1，2，…，n）为拟合平面上的三维坐标测量点时有：

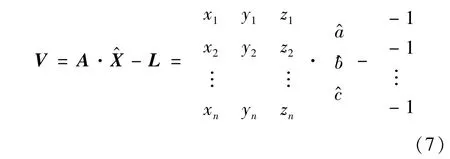
同样，以高斯最小二乘准则VTPV=min为依据，求得最优拟合参数为：

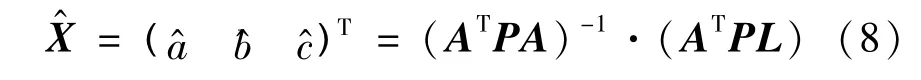
式中的权阵P为按第2.2节中所述方法经过误差分解后每个测点所确定的权值，在第一次拟合时由于平面法向量参数未知，故采用等权替代，得到平面初步参数后，重新确定每个点的权值，再进一步精确拟合求得平面参数。空间线面夹角仍然采用向量法求得，公式如下：式中，m=（a＾，b＾，c＾）为第一次等权拟合出的空间平面法向量，n为通过测站坐标和测点坐标所在直线的方向向量，则测站和测点连线与待拟合平面的线面角为与待拟合平面法向量夹角的余角。

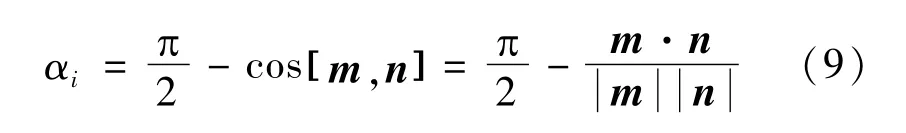
4　实验与分析

4.1仿真实验

本文实验以仿真为主，即通过数学模拟法获取标准空间线、面及其表面点，再根据测量仪器的误差特性和测站位置对模拟的表面点进行添加误差处理，使其与实际测量数据具有相同的正态随机分布误差规律，然后分别用等权拟合和EDWF拟合对模拟测点数据进行拟合计算，最后比较分析拟合结果与模拟的标准线面的参数差异或姿态差异，以此判定EDWF算法对拟合精度的影响。

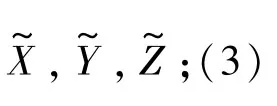
（1）空间直线仿真实验

依据测点数据模拟生成方法在设定的测距、测角误差下生成100次空间直线及其测点模拟数据，分别对每次数据进行等权拟合和EDWF拟合，然后将两次拟合结果分别与标准空间直线比较，得到两种拟合方法与标准空间直线的异面夹角和异面距离。

结果表明，100次实验拟合直线与标准直线的异面夹角，EDWF拟合较等权拟合在测角误差0.5″测距误差1+1×10-6时平均减小16.43%。100次试验拟合直线与标准直线的异面距离，EDWF拟合较等权拟合在测角误差0.5″测距误差1+1×10-6时平均减小15.73%，并对一些等权拟合结果出现偏移现象的数据有较好的修正性。

（2）空间平面仿真实验

依据测点数据模拟生成方法在设定的测距、测角误差下生成100次空间平面及其模拟测点数据，分别对每次数据进行等权拟合和EDWF拟合，然后将两次拟合的结果分别与标准空间平面比较，得到两种拟合方法与标准空间平面的夹角。

结果表明，100次实验拟合平面与标准平面的夹角，EDWF拟合较等权拟合在测角误差0.5″测距误差1+1×10-6时平均减小15.78%。

综上可知，对于空间直线和空间平面的拟合，EDWF拟合较等权拟合有较明显的精度改进，在空间姿态和空间位置上都更接近真实值。

4.2直线导轨拟合实验

实验描述：采用Sokkia NET05全站仪，测角精度0.5″，棱镜测距精度0.8+1×10-6mm，对直线导轨进行双盘位测量。由于无法得到直线导轨真实的空间参数，因此该实验采用全部19个点的等权拟合结果作为近似设计参数，而只对其中部分点（前12个点）进行拟合实验计算，根据多余观测数越多精度越高的原理，比较等权拟合和EDWF拟合与直线导轨（近似参数）的参数差异。实验结果表明，等权拟合与EDWF拟合相比近似直线参数，异面夹角分别为5′17″和3′46″，EDWF拟合减少约28.5%，该值比仿真实验略好，其原因在于实验场景的特定性和导轨近似参数偏差，以及实际仪器的测量精度与标定精度偏差所致。

5　结 论

本文提出误差分解加权拟合（EDWF）算法，根据测站—测点关系和拟合体的空间姿态将测点误差分解为纵向误差和横向误差，并以其对拟合结果的影响量为测点赋不同的权，使拟合出的几何体在空间姿态和位置上更接近实际工件。本中主要采用仿真实验的方法来验证EDWF拟合算法的性能，分别对直线和平面在不同参数下进行100次仿真实验，结果表明相比等权拟合，EDWF拟合有明显的拟合精度提升，约16%。

对于不同形状纵向误差和横向误差的分解方法是不同的，本文只针对空间直线和空间平面进行了误差分解拟合说明，对其他几何体如空间圆、球、圆柱等误差分解拟合方法将在随后的工作中进行。

［1］ Iske A，Levesley J.Algorithms for Approximation［M］. Berlin：Springer Berlin Heidelberg，2007，259-268.

［2］ Zhou Kai，Varadarajan K M，Zillich M，et al.Gaussianweighted Jensen-Shannon divergence as a robust fitness function for multi-model fitting［J］.Machine Vision and Applications，2013，24（6）：1107-1119.

［3］ 潘国荣，陈晓龙.空间圆形物体数据拟合新方法［J］.大地测量与地球动力学，2008，28（2）：92-94.

［4］ 官云兰，程效军，施贵刚.一种稳健的点云数据平面拟合方法［J］.同济大学学报（自然科学版），2008，36（7）：981-984.

［5］ 曾齐红，毛建华，李先华，等.激光雷达点云平面拟合过滤算法［J］.武汉大学学报·信息科学版，2008，33（1）：25-28.

［6］ 乔宇，黄席樾，柴毅，等.基于自适应直线拟合的角点检测［J］.重庆大学学报，2003，26（2）：29-31.

［7］ Capello E，Semeraro Q.Harmonic Fitting Approach for Plane Geometry Measurements［J］.The International Journal of Advanced Manufacturing Technology，2000，16（4）：250-258.

Industrial Measurement Fitting Algorithm for Space Line/Plane Based on Error Decomposition Weighting

PAN Guo-rong， GUO Wei， ZHOU Yue-yin
（College of Surveying and Geo-Informatics，Tongji University，Shanghai 200092，China）

In industrial measurement fitting applications，because of the measuring characteristics of instruments，error components of measurement data in different directions are difference，aiming at this problem a fitting algorithm for space line and plane base on error decomposition weighting has been proposed.Spatial attitude of workpiece and relationship between instrument and measuring points are considered.Then，influence quantity of vertical error and horizontal error on space line fitting and plane fitting are analyzed to weight measuring points.Experiment results show that compare with equalweighted fitting algorithm，this algorithm improved the fitting precision about 16%.

metrology；workpiece fitting；error decomposition；weighted fitting；industrial measurement

TB921

A

1000-1158（2015）05-0469-04

10.3969/j.issn.1000-1158.2015.05.05

2013-11-29；

2014-04-17

教育部高等学校博士学科点专项科研基金（20120072110049）；测绘地理信息公益性行业科研专项经费（HY14122136）

潘国荣（1960-），男，浙江绍兴人，同济大学教授，博士生导师，主要研究方向为精密工程工业测量与数据处理、三维可视化仿真。pgr2@163.com