孔板式电极无针头静电纺丝系统模拟

季 骥，李建军，王丽秋

（燕山大学环境与化学工程学院，河北秦皇岛066004）

孔板式电极无针头静电纺丝系统模拟

季 骥，李建军*，王丽秋

（燕山大学环境与化学工程学院，河北秦皇岛066004）

采用孔板式电极代替传统针头，用Maxwell软件模拟静电纺丝装置的静电场分布，考察了孔板电极尺寸、厚度及孔间距等因素的影响。模拟结果表明：相对于传统的针头式电极系统，孔板式电极电场更加均匀稳定，电极尺寸及厚度影响静电场的分布，而孔间距对静电场几乎无影响。适宜的电极半径R=20～25 mm，厚度H=17 mm。

孔板式电极；静电纺丝；电场模拟；电场分布

0　引言

纳米纤维是指直径在1～100 nm范围内的纤维，具有高比表面积、高孔隙率及优异的物理机械性能等优点，已引起了研究者的广泛关注。目前纳米纤维制备方法主要有：拉伸法［1］、相分离法［2］、模板合成法［3］、自组装法［4］、分子喷板纺丝法［5］、海岛型双组分复合纺丝法［6］和静电纺丝法［7］。

静电纺丝是利用注射泵将溶胶、高聚物或混合溶液引入针头，针头尖端的液滴在高压电场作用下由半球形变成锥形，也被称为泰勒锥，当外加电压使静电排斥力克服溶液的表面张力时，带电射流从泰勒锥顶端喷出然后经历鞭动、静电排斥力而持续拉伸，最后沉积到收集装置表面。静电纺丝具有工艺简单、成本低、适用于多种聚合物等特点，可制备微米级和纳米级纤维，是目前制备纳米纤维最常见的方法。目前，电纺纤维已经在生物医用材料、过滤材料、复合增强材料、传感器、电子材料等许多领域广泛应用。

传统的单针头静电纺丝装置，产量小，效率低，无法满足工业生产的需求，而多针头静电纺丝技术［8-12］，虽然提高了效率，但在纺丝时静电排斥力会导致电场分布不均，针头射流相互排斥，而且电场的不稳定变化促使“鞭动”出现，使纳米纤维定向收集困难。为了解决这些难题，研究者们设计了多种无针头静电纺丝装置：Varabhas等［13］使用带孔的圆柱形电极代替针头，纺丝液从孔中压出，在静电场中拉伸成纤维；Yarin［14］使用了双层溶液体系，下层为铁磁性悬浮液，上层为聚合物溶液，利用在磁场中铁磁性悬浮液中形成的针状突起物拉伸聚合物溶液形成纳米纤维毡；He等［15］使用气泡法静电纺丝方式，利用气流在溶液表面生成大量泡沫，在静电场的作用下，泡沫表面形成泰勒锥而拉伸成丝；Wang等［16］采用金属丝螺旋制成的锥形漏斗为电极所得的纤维直径更细，且产量成倍提高；Dosunmu等［17］采用多孔管代替针头，在高压静电作用下形成多股喷射射流，静电纺丝产量很高，但是纤维直径变化较大；Liu等［18］采用循环转动的珠链为针头，以毛刷给液的方式使转动珠链上的珠子都带有纺丝液，然后在静电场作用下不断形成射流，大大提高了纺丝产量。

为了提高规模化制备纳米纤维的取向性和有序性，本文设计了孔板式无针头静电纺丝装置，用Ansoft Maxwell 3D软件进行建模仿真，研究孔板式电极与传统针头系统的电场分布，并对电极尺寸、厚度及孔间距等参数进行了优化分析。

1　Ansoft Maxwell软件建模

1.1几何模型

为了探讨静电纺丝过程中孔板式电极对电场分布的影响，本文使用Maxwell软件对孔板电极静电纺丝装置进行了三维数值模拟。建立如图1所示模型，主要包括金属电极、孔板、接收板3部分。其中金属电极简化为实心圆柱体，半径R=25 mm，高H=5 mm；孔板为绝缘的圆柱体，半径r=30 mm，高h=8 mm，孔板上分布3个r=0.5 mm的小孔，孔间距d=13.86 mm；接收板是长宽均为200 mm，厚度为2 mm的金属板。图1中孔板到接收板的距离L=200 mm。

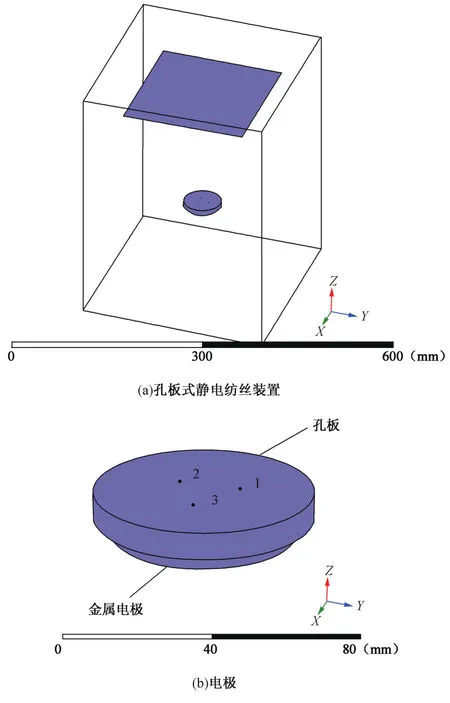
图1　静电纺丝模型Fig.1 The model of electrospinning

1.2材料属性与外加条件

金属电极为不锈钢材质，孔板采用聚四氟乙烯材质，接收板使用铝板材质；金属电极外加电压为20 kV，接收板电压为0 V。

1.3边界条件

孔板式静电模型如图1，金属电极与孔板垂直于Z轴，3号孔位于X轴10 mm处，孔板与面XOY相切；计算区域：-150 mm＜X＜150 mm；-150 mm＜Y＜150 mm；-150 mm＜Z＜250 mm，区域内为真空环境。

1.4求解条件

采用自适应方法划分网格，求解参数设置如下：残差为10-7，误差平均值为0.001，计算步骤为50。

2　结果与讨论

2.1孔板式与针头式电极对比

多针头系统中最大的难题是相邻射流之间存在排斥力，且不同位置的针头电场分布不均匀，会导致静电纺丝过程中纺丝液直接滴落或针头不工作等问题。

为了探讨孔板式电极与针头式电极的区别，在图2中给出了两种静电纺丝装置在不同位置的电场强度变化，图2（a）为Y=0，Z=1时，沿X轴电场强度变化，从图中可以看出孔板式电极在针孔表面电场较针头更均匀稳定，而且针头周围电场强度急剧下降，低于孔板表面电场强度，针头表面的电场强度为3.13×106V/m，孔表面值为3.33× 105V/m。图2（b）是X=10，Y=0时，沿Z轴电场强度变化，由图可以看出，虽然针头处电场强度远远大于孔处，但是Z值增大到70 mm时，孔的电场强度反而大于针头产生的电场。图2（c）为X=0，Y=0时，沿Z轴电场强度变化，可以发现在静电场中心区，孔板的电场强度值始终较大，且变化趋势平缓，进一步表明孔板式电极衰减小，电场均匀。

通过对比孔板式电极与针头式电极装置电场变化规律可以得到：在电压一定的情况下，孔板电极较针头电场强度值小，但是电场强度衰减小，电场分布更均匀。

2.2电极尺寸的影响

为了考察不同电极尺寸对电场分布的影响，在其他参数不变情况下，分别建立电极半径R为15 mm、20 mm、25 mm、30 mm的计算模型。图3给出了模拟计算结果，可以看出电极尺寸大小影响电场的分布：在近距离处电极越大，孔板表面电场强度越小，当距离增大到一定值后，孔板表面电场强度随电极尺寸增大而增大，电场分布越均匀。

图2　两种电极电场强度分布Fig.2 The electric field distribution of two kind of electrodes

图3（a）是Z=1时沿X轴电场强度变化，表明随着电极尺寸的增大，孔板式电极表面的电场强度降低，中间区域的电场值比两端降幅大，然而强电场区域面积增大，电场的整体均匀性较好。随着Z值的增大，在图3（b）中Z=10时沿X轴电场强度变化可以看出，电场差值减小，尺寸较大的电极中部区域电场强度反而更稳定，均匀的电场分布会使射流受力稳定，拉伸力均匀，“鞭动”不会过于剧烈，有利于得到细长纤维。但电极尺寸过大时，孔板表面的电场值较小，纺丝液受电场力较小而难以克服粘结力和表面张力，不易形成泰勒锥，这时在纺丝过程中需要增大施加电压来弥补，增大操作难度。

图3（c）是X=10，Y=0时沿Z轴电场强度变化，可以反映出电极尺寸大小对电场影响：在较近距离时（Z＜18 mm）电极尺寸越大孔板表面电场值越小，而当Z＞18 mm时，电极尺寸越大孔板表面电场值越大，因此综合考虑各种因素，规模化电纺生产中适宜的电极尺寸为R=20～25 mm。

2.3电极厚度分析

为了探究不同电极厚度对电场分布的影响，在其他参数不变的情况下，分别建立了电极厚度H为2 mm、7 mm、17 mm、32 mm的计算模型。结果如图4（a）是Z=1时沿X轴电场强度变化，图4（b）是X=0时沿Z轴电场强度变化。

从图4可以看出不同电极的厚度对电场分布的影响：随着电极厚度的增加孔板电极表面的电场强度减小，因此较厚的电极不利于在孔表面形成强电场区域，会导致纺丝过程中射流形成困难。但是当Z＞55 mm时，厚电极的场强值大于薄电极，此区域为静电纺丝过程的鞭动区，电场均匀变化有利于纳米纤维的稳定拉伸，较强的电场力反而会使鞭动剧烈，甚至出现“飞絮”现象。因此选取电极厚度时要综合考虑孔表面和鞭动区的场强变化。

从图4（b）中可以看出：H=2 mm时，孔板表面衰减幅度最大，而且接收板表面电场强度最小；H=7 mm时电场值上升幅度最大；H=17 mm时，随着Z值增大电场均匀衰减，接收板电场强度值最大；H=32 mm时，孔板表面电场增长区域变大，在Z=20 mm左右电场衰减幅度最大，而且接收板表面电场低于H=17 mm时的表面电场强度。因此，适宜的电极厚度应为H=17 mm。

2.4孔间距的影响

为了研究不同孔间距对电场分布的影响，在其他参数不变情况下，分别建立了孔间距d为13.86 mm、23.89 mm、32.33 mm的计算模型。如图5中的电场分布结果：孔附近电场强度同样存在衰减现象，曲线中出现向下的峰，峰宽约为5 mm，此范围内电场强度远远低于周围电场，因此如果孔间距过小，低电场区域叠加，不利于泰勒锥的形成，会导致在纺丝过程中出丝困难或不出丝。而且，不同间距的孔板电极产生的静电场变化趋势相似，曲线基本重合，孔的位置不同导致峰的位置不同，说明孔间距大小对电场分布影响不大。综合考虑，采用孔板式电极，孔间距d=5～15 mm范围内适宜。

图5　孔间距对电场分布的影响Fig.5 Effect of hole spacing on electric field distribution

3　结论

1）在电压一定的情况下，孔板电极比针头电场强度值小，但是电场强度衰减小，电场分布更均匀。

2）电极尺寸大小影响静电场的分布，电极半径越小，孔板表面的静电场强度越大，但电场均匀区域越小，随着Z值增大到一定值时，电极半径越大，电场均匀区域则增大，电极半径R=20～25 mm之间最佳；电极厚度越小，孔板表面的静电场强度越大，电场均匀区域减小，电场衰减增大，当Z值增大到一定值时，电极厚度增加，电场均匀区域反而增大，适宜的电极厚度应为H=17 mm。不同孔间距对静电场几乎无影响，适宜的孔间距d=5～15 mm。

［1］Ondarcuhu T，Joachim C.Drawing a single nanofibre over hundreds of microns［J］.Europhysics Letters，1998，42（2）：215-220.

［2］MaPeterX，ZhangRuiyun.Syntheticnano-scalefibrous extracellular matrix［J］.Journal of Biomedical Materials Research，1999，46（1）：60-72.

［3］Martin C R.Membrane-based synthesis of nanomaterials［J］.Chemistry of Materials，1996，8（8）：1739-1746.

［4］Whitesides G M，Grzybowski B.Self-assembly at all scales［J］. Science，2002，95（5564）：2418-2421.

［5］王新威，胡祖明，潘婉莲，等.纳米纤维的制备技术［J］.材料导报，2004，17（9）：21-23.

［6］徐红，张宝华，樊爱娟.超细海岛型纤维的制备与应用［J］.上海纺织科技，2003，31（4）：8-9.

［7］Fong H，Reneker D H.Electrospinning and formation of nanofibers［M］//Salem D R.StructureFormationinPolymericFibers. Munich：Hanser，2001：225-246.

［8］Theron S A，Yarin A L，Zussman E，et al.Multiple jets in electrospinning：experiment and modeling［J］.Polymer，2005，46（9）：2889-2899.

［9］Tomaszewski W，Szadkowski M.Investigation of electrospinning with the use of multi-jet electrospinning head［J］.Fibers and Textiles in Eastern Europe，2005，13（4）：22-26.

［10］Angammana C J，Jayaram S H，Effects of electric field on the multi-jet electrospinning process and fiber morphology［J］.Transactions on Industry Applications，2011，47（2）：1028-1035.

［11］Xie S，Zeng Y C.Effects of electric field on multineedle electrospinning：experiment and simulation study［J］.Industrial and Engineering Chemistry Research，2012，51（14）：5336-5345.

［12］Yang Y，Jia Z D，Li Q，et al.A shield ring enhanced equilateral hexagon distributed multi-needle electrospinning spinneret［J］. Transactions on Dielectrics and Electrical Insulation，2010，17（5）：1592-1601.

［13］Varabhas J S，Chase G G，Reneker D H.Electrospun nanofibers from a porous hollowtube［J］.Polymer，2008，49（19）：4226-4229.

［14］Yarin A L，Zussman E.Upward needleless electrospinning of multiple nanofibers［J］.Polymer，2004，45（9）：2977-2980.

［15］He J H，Liu Y，Xu L，et al.Biomimic fabrication of electrospun nanofibers with high-throughput［J］.Chaos Solitons&Fractals，2008，37（3）：643-651.

［16］Wang X，Niu H T，Lin T，et al.Needleless electrospinning of nanofibers with a conical wire coil［J］.Polymer Engineering and Science，2009，49（8）：1582-1586.

［17］Dosunmu O O，Chase G G，Kataphinan W，et al.Electrospinning of polymer nanofibres from multiple jets on a porous tubular surface［J］.Nanotechnology，2006，17（4）：1123-1127.

［18］Liu S L，Huang Y Y，Zhang H D，et al.Needleless electrospinning for large scale production of ultrathin polymer fibres［J］.Materials Research Innovations，2014，18（4）：833-837.

Investigation of electric field simulation on plate-holes needleless electrospinning system

JI Ji，LI Jian-jun，WANG Li-qiu
（School of Environmental and Chemical Engineering，Yanshan University，Qinhuangdao，Hebei 066004，China）

A plate-holes spinneret needleless electrospinning equipment instead of needles spinneret was developed to study the electrostatic field distribution.The effect of plate-holes electrode size，thickness and hole spacing was analyzed using Ansoft Maxwell software.The simulation results show that plate-holes electric field distribution is more uniform and stable than needles electrode，the size of plate-holes electrode and thickness affect the distribution of electrostatic field，but the hole spacing has little influence on the electrostatic field.The best electrode size is the radius R=20～25 mm and thickness H=17 mm.

plate-holes electrode；electrospinning；electric field simulation；electric field distribution

TQ340.6

A DOI：10.3969/j.issn.1007-791X.2015.06.006

1007-791X（2015）06-0506-05

2015-08-15 基金项目：河北省自然科学基金资助项目（B2015203259）

季骥（1990-），男，河北沧州人，硕士研究生，主要研究方向为静电纺丝制备功能及结构纤维材料及规模化研究；*通信作者：李建军（1974-），男，河北迁安人，博士，副教授，主要研究方向为新型无机纤维材料的制备及应用，Email：jianjunli@ysu.edu.cn。