基于二次曲面的点云数据三维重构
2015-10-24李耀辉武志峰宣兆成
李耀辉,武志峰,宣兆成
(天津职业技术师范大学信息技术工程学院,天津300222)
基于二次曲面的点云数据三维重构
李耀辉,武志峰,宣兆成
(天津职业技术师范大学信息技术工程学院,天津300222)
针对传统三维重构依赖三角网格且难于有效分割含缺陷的点云数据的问题,将点云数据的三维重构转化为曲面片的光滑拼接问题。本文定义一个二次曲面片的模板方程并采用待定系数法构造曲面片,利用结式方法实现不同曲面片的光滑拼接使三维造型光滑逼真。为了克服二次曲面不易作图的缺点,讨论了采用一次平面方程近似处理的方法。该方法可得到曲面片以及拼接曲面的解析表达式,具体重构时直接代入点云数据即可得到相应的方程,具有高效实用的特点。
三维重构;点云数据;曲面拼接;结式
三维扫描实现了三维物体的数字化,但获取三维点云数据后,如何实现高效逼真的三维重构是人们研究的问题之一[1-3]。很多学者提出了不同方法。一般方法是采用Delaunay三角剖分方法,根据点云数据对三维物体进行重构。该方法的最大优点是简单,且只要三角形足够小就可达到要求的精度。文献[4]提出采用possion方程重构三维造型的方法,但该方法涉及指数函数的计算,因此复杂度较高。另外传统点云分割方法往往依赖点云的三角网格,很难有效分割含缺陷的点云,需借助复杂的数据结构或算法[5]。因此,人们对于点云数据的处理提出了各种不同的方法[6-7]。随着计算机性能的提高,人们不再局限于使用一次函数拟合或分段拟合实现三维造型。目前,人们在计算机辅助设计中可使用不高于10次的多项式函数来表示几何造型或三维重构中物体的数学模型。从选择曲面片的角度考虑,曲面的次数越高,其拐点可能越多,也可能产生奇异点。为此,将符号消元的结式方法用于点云数据的三维重构[8],提出采用二次函数结合曲面拼接的方法实现三维重构。重构过程中,所有曲面片均采用正则曲面片去重构物体的几何造型。若实际的几何造型存在奇异点,则将造型中的曲面片进行分解直至正则为止。然后,用二次曲面去重构几何物体。该方法通过选择n个点云数据并拟合成曲面片,当多个曲面片能够相互覆盖不产生孔洞时即可构成三维重构的曲面。同时,由于点云数据中相互关联点之间的欧氏距离比较小,因此精度可满足三维曲面重构的要求。
1 曲面片的构造
1.1拟合点组的选择
如前所述,通过接触式或非接触式方法可以很容易得到物体的三维点点云数据,点云数据及三维重构如图1所示。图1(a)为奶牛模型的点云数据,整个点云由2 903个点构成。采用Delaunay三角形网格对点云数据重构得到的结果如图1(b)所示,该图由5 804个三角形网格构成。在本文中,为实现物体二次曲面片的三维重构,首先确定一个点,然后以此点为左上点并搜寻与其相邻的其他3个点,这样4个点构成一组。最直接的方法是将所有点云数据按某一坐标从小到大排列,然后4个点为一组,分别将各点的坐标值代入模板方程得到含有4个线性方程的方程组。计算出方程各个系数的值,得到一个次数为2的曲面片方程,最后得到797个曲面片。之后,从4个点中分别选取三维坐标的最小值和最大值画图,由此得到的奶牛造型如图1(c)所示。撇开造型的完整性,该造型需要的曲面片更少。另外,每个面片是二次曲面,通过二次曲面在不增加面片个数的情况下可以减小误差,提高造型的光顺程度。但该方法得到的点组太少,不能构造出连续的曲面。

图1 奶牛的点云数据及三维重构
该造型中所有曲面片没有连接起来构成一个完整的造型,因此并不理想。最直接的想法是计算出二次曲面后直接增大曲面片的覆盖范围,这样会增大拟合的误差,从而使造型不光滑。因此,如何在保证光滑程度的情况下将断续的曲面片连接起来得到理想结果是算法研究的关键。
1.2曲面片构造的具体方法
利用所有的点云数据拟合出一个多项式方程描述物体的三维造型方法虽然直观,但不现实。主要原因是点云的数据量通常很多,从几千到几万甚至几十万个,这样拟合出的多项式的次数很高,且计算复杂。为此,利用点云数据中的少量数据拟合曲面片,将曲面片拼接起来构造物体的三维造型。
考虑二次曲面的一般形式为f(x,y,z)=ax2+by2+ cz2+dxy+exz+fyz+gx+hy+iz+j。该方程有10个系数,可以选择点云中的10个点确定一个二次曲面。如果一个曲面片中尽可能包含多个点,作图时可以采用更少的曲面片,从而增加拟合的速度和作图的效率。然而,直接采用该形式且将10个点分为一组代入方程,用待定系数法求解,会遇到许多问题。第一,得到的线性方程组可能会无解。从造型的角度考虑点云数据具有很强的关联性,但是从数据本身考虑,则具有很大的随机性,选择的点不在一个二次曲面上。如果代入f(x,y,z)之后并求解,所求的各项系数均为0,即方程只存在零解。但是,此结果对于拟合曲面片无意义。第二,二次曲面包括双曲面、椭球面、抛物面等不同的类型。特别是当拟合出双曲面时,虽然曲面由一个方程表示,但拟合时采用的点可能出现在2个分支上。此时,这样的面片重构出来的几何物体也是不连续的。另外,考虑采用球面片而没有采用抛物面等其他二次曲面,是因为球面片各个方向同性。如果采用抛物面,当拟合曲面的轴线与坐标轴不平行时需要考虑旋转等问题。这样会导致曲面片的方程复杂,降低算法的效率。第三,拟合结果可能会分解为2个一次函数。从点云中选择点的位置具有一般性,在有些情况下得到的二次函数能够进行因式分解,从而生成2个一次因式。特殊情况下,9个点的拟合结果如图2所示,图中的9个点拟合出的曲面分解为交叉的2个平面。
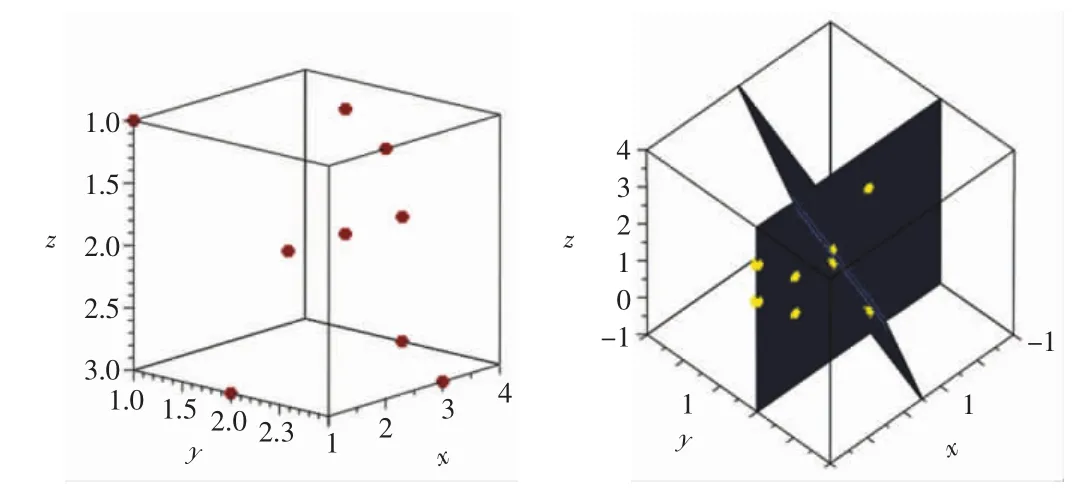
图2 特殊情况下9个点的拟合结果
为此,考虑二次曲面特性的一致性且保证在任何情况下待定系数法非零解的存在,采用球面片作为所要拟合的曲面,选择二次方程T=a1(x2+y2+z2)+a2x+ a3y+a4z+a5作为模板。T中有5个参数,拟合二次曲面时采用待定系数法确定参数ai(1≤i≤5)的值。通过这5个参数可以确定曲面片的球心坐标、半径等。重构时,不同位置可以用不同的球面片表示。具体拟合时,将点云的每4个点做为一组。这样,将4个点的坐标值代入模板方程后,生成由4个方程构成的关于ai的线性方程组。由于方程组有5个未知数,因此方程组的解表示为其中一个系数ai的解析式。
造型时需要得到具体的数值解,因此对解析解中保留的ai进行归一化处理得到所表示的曲面片。计算曲面片时,之所以选用4个点而没有选择5个点,主要是保证每次计算时能够计算出方程的解,可以得到曲面片。另外,选择4个点可以保证得到的是球心位置和半径不同的球面片,从而保证各个球面片连接的连续性。
2 造型中曲面片的光滑拼接
几何造型是由二次曲面片组成,奶牛蹄部的2个曲面片的连接效果如图3所示。从图3中可以看出,每个曲面片各有4个点拟合而成且它们拥有共同的2个点。采用三角网格进行拼接,构造出的三角形中至少有1条公共边即可。当采用二次曲面时,2个曲面片在边界处的效果如图3中的中间造型所示,它们并没有光滑地连接在一起。因此,这些曲面片在边界处的拼接是接下来要处理的问题。

图3 几何造型中部分曲面放大后的效果
只有2个在边界处连接的曲面才需要光滑拼接,因此需要判断2个曲面拼接的必要性。从图3可知,2个曲面中至少有2个交点,每1个曲面由4个点拟合而成。设Pi为拟合曲面Si的点集,当#(Si∨Sj)=6时才需要进行拼接,其中#()表示集合中的元素数。
为提高拼接的效率且降低拼接的复杂度,实现拼接有几种方法。实际造型中有多种曲面片连接的情况,如图4所示。
如果一个曲面片连接4个曲面片,则在拼接时将中间曲面转换为过渡曲面且过渡曲面在边界处过渡为其余4个曲面的方程。更多情况类似于图4(a)点1~4拟合出第1个曲面片,点3~6拟合出第2个曲面,点5~8拟合出第3个曲面片,这些曲面之间的连接,被称为级联式连接。在级联式拼接中将中间固定,即在第一节得到的曲面方程不变,通过选择合适的参数使连接它的曲面稍微改变,便可保证边界处实现光滑拼接。具体方法是:对于第1、2个曲面片,点3和点4是它们共有的点,因此认为整个曲面从点1和点2生成的边界沿着与边界垂直的方向逐渐过渡,当到达点3和点4生成的边界时变成曲面片2。这样,将2个曲面片的方程做为主曲面方程s1和s2。计算拼接曲面时,为了实现较好的光照效果,选择的辅助曲面应是拼接处曲面的法向方向。然而,因为点1和点2生成的边界方向的垂直方向难于计算,且精确计算会增大计算量。因此,采用近似的方法确定法向分量。
比较从点1到点3或点2到点4变化过程中,判断坐标x、y、z中哪一个分量变化最大。为尽可能准确地确定拼接的方向,计算曲面s1的中心坐标,即
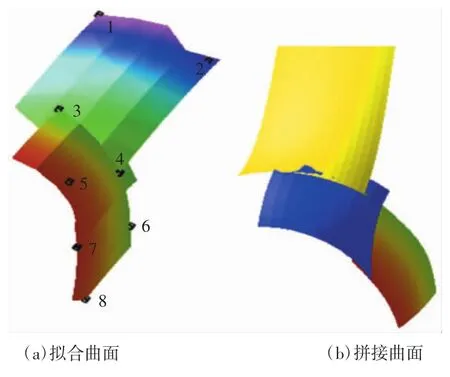
图4 多个曲面的光滑拼接

其中:u分别取x、y、z。然后,计算s2的中心坐标v2u并得到每个坐标方向的差值vs=|v2u-v1u|。最后,确定连接方向u为vs值最大的方向。进一步选择该分量构造辅助曲面h1=u-v1u和h2=u-v2u。这样,可以构造一组方程

通过式(1)可以看到,在辅助曲面h1时对应主曲面s1,当辅助曲面过渡到h2时主曲面也到达s2。辅助曲面仅表示位置关系,即在u取最小值时主曲面取s1,u取最大值时主曲面取s2。然后,利用结式消元法计算过渡曲面,计算完毕后得到过渡曲面bs,用bs代替曲面1实现曲面片的光滑拼接,最后的拼接效果如图4(b)所示。
但由此引起的问题是,原来拟合出的曲面通过点云中所规定的点,新生成的曲面片是否能满足精度要求。通过u1、v1计算得到的过渡曲面为因为bs在初始位置即辅助曲面取h1时,bs与h1相交得到的曲线和s1与h1的相交曲线的方程相同,因此必通过点1和点2。当曲面过渡到点3和点4时,曲面方程过渡为s2。因为点3和点4是曲面1和2的公共点,所以过渡曲面bs也一定通过点3和点4。因为通过点1~4的二次曲面不止一个,该方法可以理解为在已知的一个曲面上计算得到与另外一个曲面片在指定位置光滑拼接的另一个曲面片。另外,因h和s分别是一次和二次多项式,由此可知deg(bs)≤4。因此,可采用不高于4次的多项式方程实现所有曲面片的G1阶光滑拼接。利用光滑拼接法得到的不同点云数据的几何造型如图5所示。
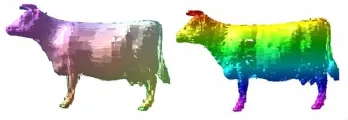
图5 采用曲面拼接的三维重构
3 曲面片大小的调整
由三角网格变为二次隐式曲面,并不仅仅是选取4个点并利用待定系数法得到二次曲面的问题。为保证造型的光滑性,研究希望点云数据得到曲面片的边界如图3虚线框内的二次曲面。由于作图时取值范围的限制从而出现多余部分和缺失部分。因此,在作图时采用近似二次球面的方法。
具体实现时,用多个三角形面片代替二次曲面,三角面片的个数根据作图时的精度确定。最基本的精度是每个二次曲面由4个三角面片逼近。由前面的描述可知,每个面片由4个点构成且中心坐标为v1u,但该点不一定在球面上。将这4个点用直线连接构成的图形是凸的且中心必在其内。因此,中心点在球面片上有一对应的实数点,将中心坐标的任意2个代入球面方程T就可计算出另外一个坐标的值,即得到球面片的相应点v′。
在实际计算中会遇到3个问题:①法线的内外问题。因为球面方程的次数为2,所以中心点映射到球面上有2个点。但是,在实际造型中选择哪一个点要利用点云的性质确定,即点云之间的距离不大,中心点距球面上映射点的距离就不会很大。在造型时,选择球面上距离中心点v′较近的点构造三角面片。②浮点数计算问题。点云坐标都带有小数位,其精度达到10-6甚至更高,在计算过程中会带来浮点数的计算问题,即中心点对应球面片上的点是实际存在的。理论上,将球面包括范围内任意点的x、y、z坐标中的2个代入球面方程计算出的第3个值应是一个实数解。但由于浮点计算问题得到的许多解是复数,从而给作图带来了困难。为此,当得到复数解时仅取其实数部分。这样计算得到的点将不会在球面上。经实际作图和计算,当点云中相邻2点各个方向上的坐标差为10-2时,仅取复数实部代入方程后的误差为10-3,精度可以满足要求。③作图的精度问题。用三角形面片代替球面片实质是用一次方程代替二次方程。为了提高作图的精度,必须采用尽可能多的三角面片逼近球面片,三角形的个数需根据作图时的精度确定,最基本精度是v′与4个点构成4个三角面片。当精度要求更高时,可由点云相邻2点的中点计算出其映射到的球面上点。这样,可以用8个三角形面片来代替球面片。类似地,还可以继续提高精度来逼近球面片。采用该方法得到的实际几何造型如图6所示。从图6中可以看出,奶牛的造型腹部后半部分是鼓起来的。

图6 曲面调整后的结果
4 结束语
为实现点云数据曲面片的重构,将4个点云数据分成一组。一组数据的部分数据可能存在于不同曲面片中,因此点云数据可能重用,但是次数不能超过4次以上。将数据代入二次方程并利用待定系数法求解出二次方程的系数。此时,得到的曲面片仅能够实现G0阶拼接。为了实现不同曲面片之间的G1阶光滑拼接,通过结式消元法得到2个曲面片中一个面片的近似曲面。该近似曲面仍通过原曲面求解时的4个点云数据的坐标。实例表明,该方法较好地实现了真实物体的几何造型。另外,符号计算中的所有结果都是离线完成得到的解析解,具体计算时只需将点云数据代入公式便可直接得到结果,既可满足精度要求又具有较高的效率。
[1]莫堃.基于隐式函数的曲面重构方法及其应用[D].武汉:华中科技大学,2010.
[2]NIELSON G,HAGEN H,LEE K.Implicit fitting of point cloud data using radial hermite basis functions[J].Computing,2007,79(2):301-307.
[3]YOO D.Rapid surface reconstruction from a point cloud using the least-squares projection[J].International Journal of Precision Engineering and Manufacturing,2010,11(2):273-283.
[4]武敬民.三维点云处理及隐式曲面三维重构技术的研究与实现[D].太原:中北大学,2014.
[5]邹万红.大规模点云模型几何造型技术研究[D].杭州:浙江大学,2007.
[6]EMELYANBOV A,SKALA V.Surface Reconstruction From Problem Point Clouds[P].Graphicon,2006:239-247.
[7]MOENNING C,DODGSON N.Intrinsic Point Cloud Simplification[P].Graphicon,2006:110-125.
[8]李耀辉,武志峰,宣兆成.基于结式的曲面拼接与三维造型[J].计算机应用,2015,35(10):2950-2955.
Three dimensional reconstruction of point cloud data based on quadratic surface
LI Yao-hui,WU Zhi-feng,XUAN Zhao-cheng
(SchoolofInformationTechnologyandEngineering,TianjinUniversityofTechnologyandEducation,Tianjin300222,China)
As to the problem that traditional 3D reconstruction relies on triangular mesh and it is difficult to effectively segment the point cloud data with defects,the 3D reconstruction of point cloud data is transformed to the smooth blending of curved surface.A quadratic surface patches template equation is defined and the undetermined coefficient method is used to construct the surface,the resultant method is used to realize smooth connection of different patches,which can make 3D modeling smooth and realistic,and overcome the problem that it is not easy to draw the quadratic surface.The ways how to use a plane equation approximation method are discussed.The method can analyze surface and blending expressions,and the specific reconstruction for the point cloud data can be obtained by corresponding equations.The method has high efficient and practical features.
3D reconstruction;point cloud data;surface blending;resultant
TP391.41
A
2095-0926(2015)04-0005-05
2015-10-17
天津市科技支撑计划项目(14ZLZLZF00031);天津职业技术师范大学科研发展基金项目(KJY12-09);天津职业技术师范大学留学回国基金项目(RC14-50).
李耀辉(1968—),男,教授,博士,硕士生导师,研究方向为算法设计及优化、符号计算等.
